基于仿真可信度评估的变压器模型参数优化

应 婷，李江红

（中车株洲所电气技术与材料工程研究院，湖南 株洲 412001）

0 引言

仿真可信度指仿真系统与被模拟系统在功能上的相似程度[1-2]，其是合理利用仿真结果的基本前提。随着仿真技术的发展及其应用领域的拓宽，对仿真结果的正确性和可信度要求越来越高，如何提升系统仿真的可信度已成为系统仿真目前迫切需要解决的一个问题[3-4]。影响仿真可信度的因素主要包括模型结构、模型参数、不确定性数据、评估方法及误差累计等，其中模型结构和模型参数的影响最大。模型结构通常根据理论原理进行设计。对于电气系统而言，数学模型建模基于微分方程建模，大部分公式为公知的且结构相对固定；而模型参数却因测量方法、工艺设计、使用环境、老化等因素，其数值可能与理论值存在偏差，这将对仿真结果产生较大影响，甚至可能导致可信度大大降低。建模人员往往对参数的输入范围、对结果的影响程度、仿真结果的偏离程度缺乏直观和量化的认知，调整参数主观性、随意性强，致使结果正确性不能得到保障。

仿真系统的校核、验证与确认（verification,validation and accreditation, VV&A） 是仿真系统可信度评估的重要手段之一，通过对仿真系统成果的正确性进行评估，从而保证仿真系统达到足够高的可信度水平以满足应用的需要[5]。仿真可信度评估过程包括校核、验证与验收3部分内容。其中，验证侧重于对仿真结果的检验，即将试验结果与理论结果进行比较从而验证数学模型的有效性，即获得仿真的可信度。国外自20世纪50年代末开始对仿真可信度评估进行研究，至今取得了较多成果。如，文献[6]提出了一套开发和验证多智能体仿真系统的方法，文献[7]提出了基于向量自回归模型的多智能体模型验证方法。国内相关研究起步于20世纪80年代，在评估理论方法方面主要以跟踪国外研究为主，如对基于相似度的方法、基于层次分析方法等进行改进以满足实际应用需求。文献[8]从离散状态一致性的角度对仿真可信度进行评估；文献[9]提出了基于可信度评估网(CESN)的网络化指标体系构建方法和缺陷追溯方法；文献[10]给出了半实物仿真系统的可信度评估思路与方法。

近年来，轨道交通领域对于仿真可信度的要求也越来越高，但目前该项研究工作还处于起步阶段，主要进行定性分析，没有给出具体的量化指标。研究如何对仿真结果与实际数据的误差进行数值分析，以此提高仿真可信度，具有重要的价值和应用意义。因此，本文以牵引变压器为研究对象，根据其数学原理构建仿真模型，以仿真数据与试验数据对比计算的可信度为优化目标；结合最优化问题的求解需求选择输入信号，通过敏感性分析选择优化参数，建立优化模型进行关键参数优化，通过减小参数偏差达到缩小仿真结果与试验结果误差的目的，提升变压器仿真模型准确度。

1 牵引变压器原理及仿真模型

牵引变压器又称机车主变压器，主要用于电压变换、隔离、滤波及保护。根据绕组接线方式可推导出变压器主从侧之间的关系，搭建牵引变压器数学模型。忽略变压器二次侧绕组间的互感，针对变压器的励磁阻抗，建立励磁电路模型[11]。用一个电感-电阻回路等效变压器一次侧绕组与任意一个二次侧绕组之间的短路阻抗，并将参数折算到变压器二次侧。虽然精细化的T型等效电路能更精准地模拟各变量物理情况，但模型需包括多个串联、并联回路，解算较为复杂。因此，将励磁支路前移，使之与电源并联，得到只有励磁支路和负载支路并联的Γ型等效电路，不仅大大简化了计算，而且精度同样能得以保障。图1示出某交流电力机车的三绕组牵引变压器二次侧的简化等效电路，其中Un和In为变压器一次侧额定电压和额定电流；US为变压器一次侧折算电压；K为理想变压器变比；US1,US2,US3为变压器二次侧电压；IS1,IS2,IS3为变压器二次侧电流；Im为励磁电流；Rm为励磁电阻；Lm为励磁电感；R1,R2,R3为变压器绕组电阻；L1,L2,L3为变压器绕组漏感。

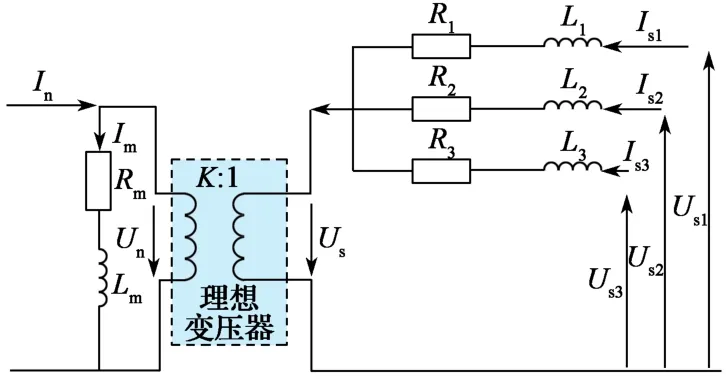
图1 牵引变压器简化等效电路Fig.1 Simplified equivalent circuit of traction transformer

根据牵引变压器等效电路（图1），按照基尔霍夫定律计算变压器绕组漏感、网侧电流以及二次侧电压：

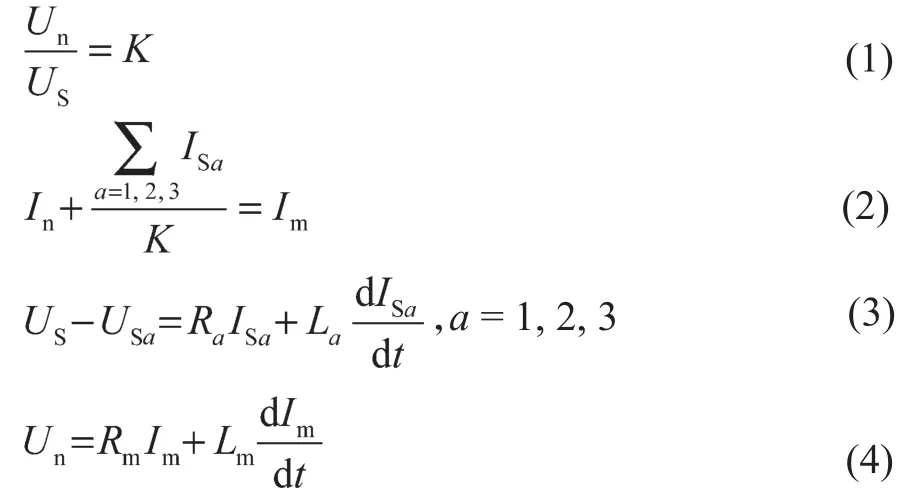
根据式(1)～式(4)搭建变压器仿真模型（图2），其输入信号为一、二次侧电压，输出信号是为一、二次侧电流。由于主电路后端电路可能出现断路状态，因此在变压器仿真模型中需要设置使状态量置零的功能。其通过接收充电电路接触器关断状态信号和整流器桥臂截止信号，判断充电电路接触器是否均关断或整流器桥臂是否截止，若是，则将输出电流直接置零。

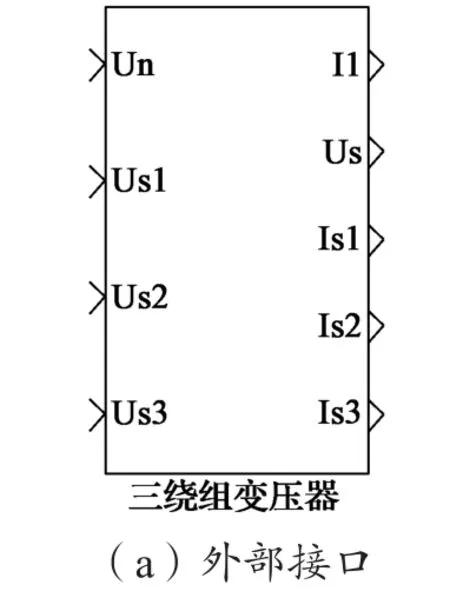
图2 变压器仿真模型Fig.2 Simulation model of transformer

2 牵引变压器模型参数优化设计

仿真模型输出结果与实际结果的差异越小，模型的价值则越大,以此为模型优化的目标。仿真可信度是评估该误差的定量指标，即选择仿真可信度作为参数优化的目标函数，获得目标函数极小值。常用方法包括有基于相似度的可信度定量分析和残差分析两种，下面分别进行介绍。

2.1 优化目标函数

2.1.1 基于相似度的可信度分析

相似度是基于仿真系统和实际系统的比较[12]，强调了仿真可信度的客观性，其决定性因素主要包括系统间相似单元数目、单元数值及单元权重。

根据可信度层次性的特点，将大系统分解成若干个子系统或模块，分别进行可信度评估；然后再根据这些对象的可信度结果、层次及耦合关系，确定仿真系统整体的可信度。首先假设在单项试验获取了实际测试的数据，由k个要素组成；参照该单项试验获取仿真数据，由l个要素组成；假设这些要素之间存在n个相似元，则第j个单项试验（或曲线）的可信度定义为

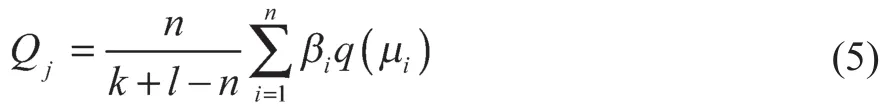
式中：βi——相似元对系统相似程度影响的权重，；q(μi)——第i个相似元的相似度。

对于q(μi)，其计算式如下：

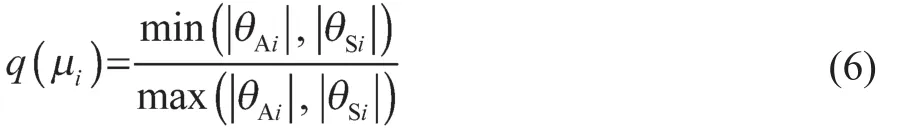
式中：θAi——实测数据；θSi——仿真数据。

加入每个单项试验仿真的可信度权重系数，可计算出某项试验仿真的可信度：

式中：M——试验项目总数；λj——第j项试验的仿真可信度权重系数，。

λj根据单项试验对整个试验的重要程度决定，与相似元权重系数的确定原则一致。

2.1.2 残差分析法

残差分析法是先将仿真信号序列减去实测信号序列，得到残差序列，然后再对残差序列建立适当的数学模型，并给出相应的数值指标[13]。具体表达式如下：

式中：{yi,i=1, 2, …,n}——实测序列；——仿真序列；xi——第i点信号的可信度；γi——第i点的权重系数；φ——仿真信号与实测信号的残差指标。

2.1.3 相似度和残差分析的一致性

综上可知，残差分析的核心是

对式(11)进行如式(12)所示变换，则可得知残差分析的本质和基于相似度的计算原理是相同的，这也说明了两种方法对可信度描述的一致性。

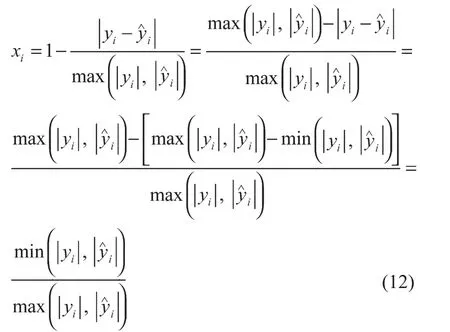
因此，可以选择其中一个作为最优化目标函数：

2.2 选择输入信号

变压器理想工况为输入的电压和电流波形均为单一频率的光滑正弦波，但由于理想输入信号单一，变压器模态不能被完全激励，因此参数辨识和优化将存在盲区。为简化分析，下面以单相单绕组变压器为例进行说明。假设其一次侧电流表达如下：

式中：An,AS1——变压器一、二次侧电流幅值。

对电流求导，可得：

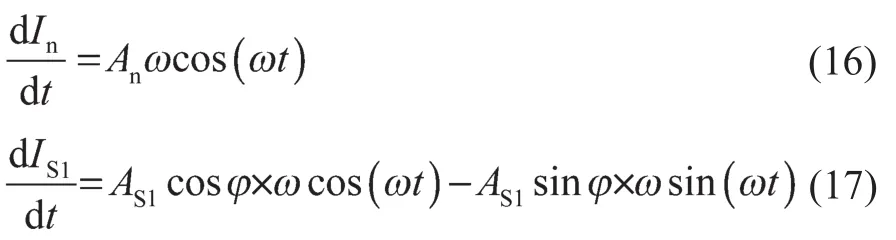
将式(16)、式(17)、式(1)和式(2)代入式(3)和式(4)，得：

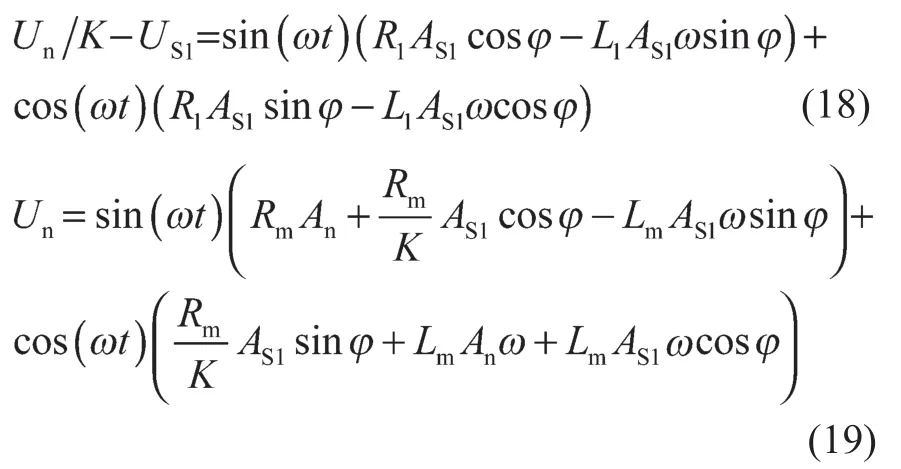
根据数学原理，仅凭式(18)和式(19)无法求解出K，Rm，Lm，R1，L1这5个未知数，也就是说该系统模态未被完全激励。如果变量中包含丰富的谐波成分或非周期分量，如2，3，5，7次谐波等，具体见式(20)，则利用式(18)和式(19)，模态可以被完全激励，上述5个未知数就可以完全被辨识和优化。

式中：A——电流幅值；ω1——基波角频率；ω2——2次谐波角频率；λ——非周期分量时间常数。

根据上述分析，参数优化所需的输入信号必须包含充足的过程特性信息，不能任意选择。为了使所有参数均被优化，输入信号必须满足能够激励所有参数的基本要求。在最优化问题中，输入信号的频谱要求必须包括过程的全部频谱[14]。例如参数辨识时，若目标参数是N个，则要求输入的激励信号必须包含超过N/2个不同频率的成分。因为每个频率响应存在着虚部和实部，两个对应关系只能解出两个未知数。参数优化时,对输入信号同样有着优良性的要求，即输入信号的选择能使参数优化后的模型精度最高。由于轨道交通牵引变压器的二次侧输入电压为开关脉冲信号（图3），其含有丰富的谐波分量，且便于工程测量，因此本文分别选用变压器一次侧和二次侧电压的试验数据作为输入，来进行参数优化。

图3 输入信号示例Fig.3 Examples of input signal

2.3 优化方法及参数选择

本文选用梯度下降法进行参数优化。梯度下降（gradient descent）是迭代法中的一种，优化思想是用当前位置负梯度方向作为搜索方向，因为该方向为当前位置的最快下降方向，所以也称之为“最速下降法”。最速下降法越接近目标值，步长越小，前进越慢。在求解机器学习算法的模型参数时，梯度下降是最常采用的方法。在求解损失的最小值时，可以通过梯度下降法来一步步地迭代求解，得到最小化的函数和模型参数值。

变压器Γ形等效电路涉及的关键参数包括：一、二次侧绕组变比K；励磁电抗Lm；励磁电阻Rm；变压器绕组电阻R1,R2,R3；变压器绕组漏感L1,L2,L3。

一般而言，变压器漏感由其绕组的尺寸、形状、匝数等结构参数和布置方式等决定，而励磁电感则与铁心饱和特性及状态强相关。为提高优化效率，判断参数对结果的影响程度，需要寻找高敏感性参数。首先设置变压器参数及范围，然后按随机分布方法生成分析数据。由于在一次侧绕组电压一定的情况下，变比可以通过二次侧绕组体现，因此选择一次侧绕组电压拆算到二次侧的额定值V2作为参数。对分析数据中的参数进行多次计算，根据参数对结果的影响程度，得出敏感性排序。对上述变压器模型及参数进行敏感性分析，结果如图4所示。可以看出，V2,L2和R1为敏感性最强的参数，因此后续主要针对这3个参数开展优化工作。

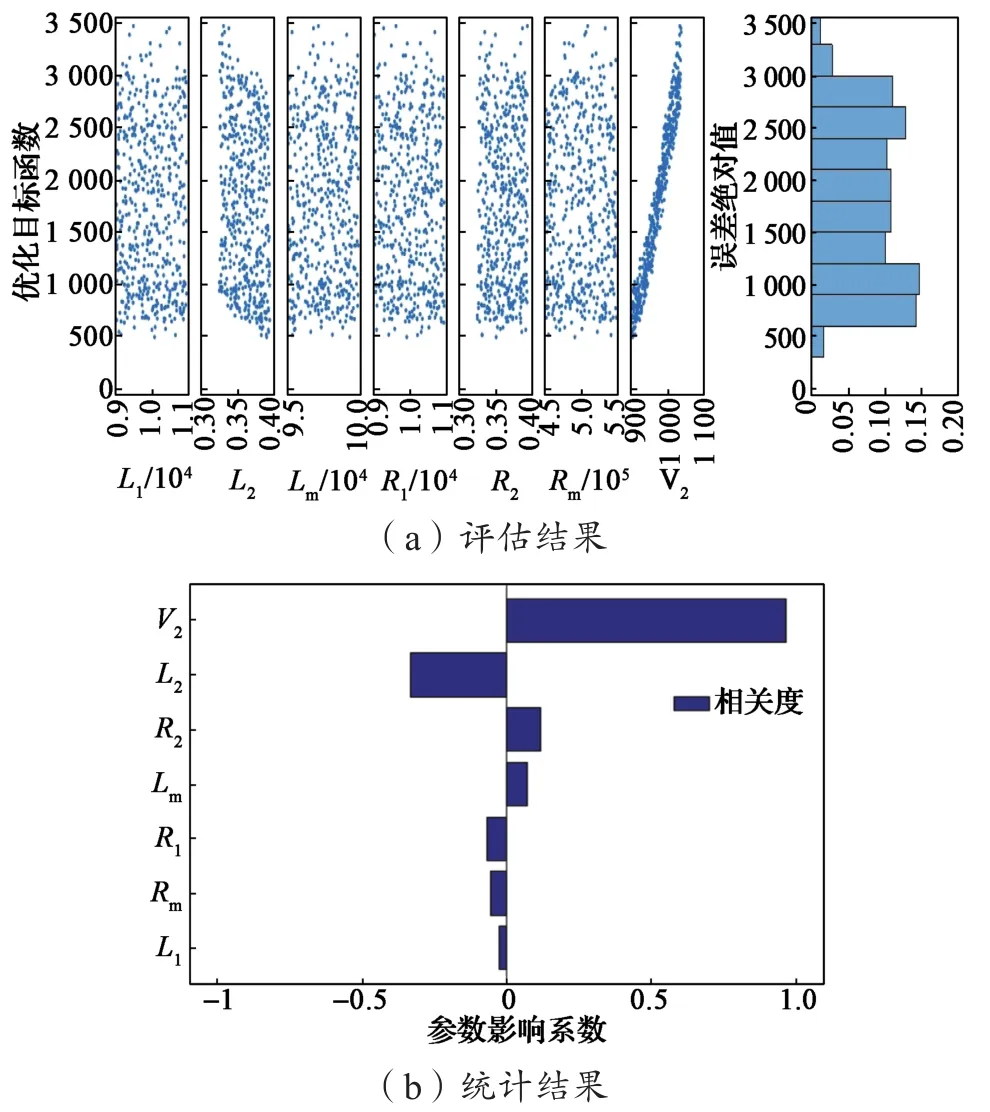
图4 敏感性分析结果Fig.4 Sensitivity analysis results

3 以仿真可信度为目标的变压器模型参数优化

根据第2节所述模型参数优化设计方法，以变压器为对象，开展以仿真可信度为目标的模型参数优化。首先，以实测试验数据驱动仿真模型，即分别将变压器一、二次侧输入电压试验数据作为受控电压，观测模型二次侧输出电流仿真数据。然后，比较模型所计算的仿真数据与试验数据的偏差，通过对可信度指标的计算，定量分析仿真数据和试验数据之间的差别，以此判断可信度是否达到最优。如果可信度最优为“否”，则进行参数优化计算，并将优化后的参数输入到模型中进行对比判定，经过多次迭代，直至可信度最优为“是”，输出最优参数。

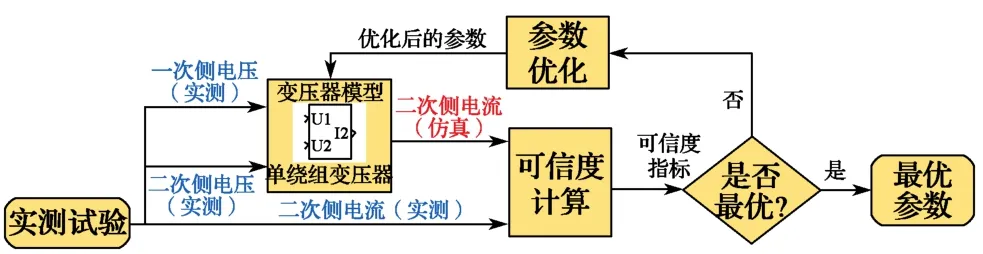
图5 变压器模型测试流程Fig.5 Process of transformer model optimization

变压器默认参数为一次侧折算电压25 kV/50 Hz，二次侧折算后电压970 V，二次侧电阻R2为0.36 Ω，短路阻抗百分比36%。现有仿真通常采用默认参数计算仿真模型，输出仿真数据。选取10次真实的试验数据，与仿真数据对比，经过定量仿真相似度分析，结果如表1所示。经计算，其可信度为

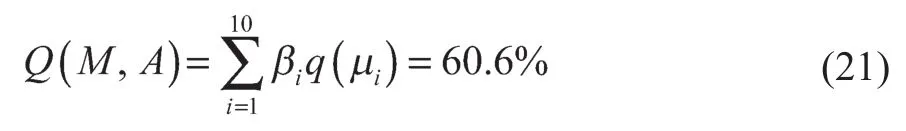
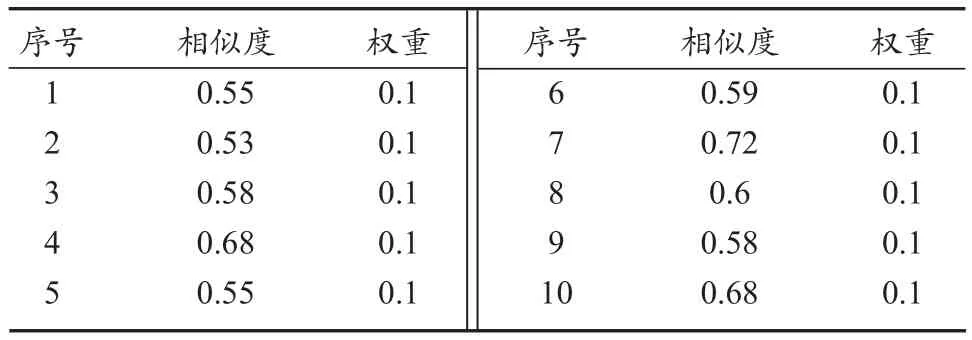
表1 参数优化前，试验数据与仿真数据相似度分析Tab.1 Similarity evaluation of measured data and simulation data before parameter optimization

选取其中一次仿真数据与试验数据进行对比（图6），可以看出，已知的默认参数仿真可信度较低，定量分析与定性分析结论一致。

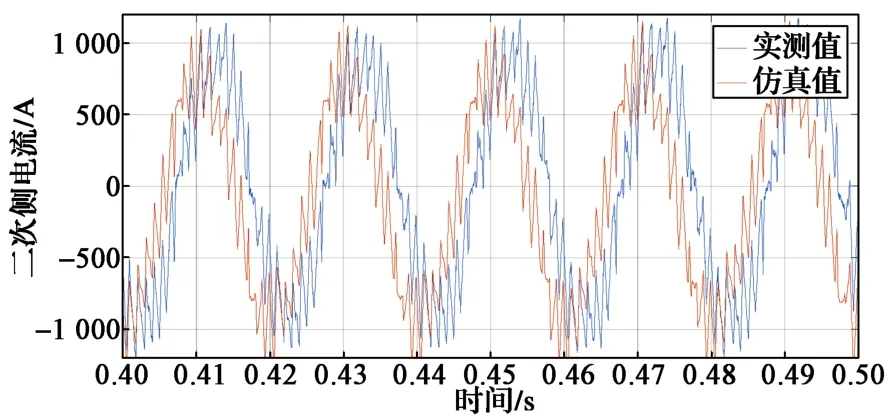
图6 参数优化前，试验数据及仿真数据对比Fig.6 Comparison between measured data and simulation data before parameter optimization

选取整个10段试验数据进行变压器模型参数优化，设置参数初始值为默认参数，变比参数优化范围设置为±10%，短路电阻电感参数范围设为0～50%（标幺值）。使用梯度下降法寻找最优参数，以满足可信度最小的优化目标函数，优化过程曲线如图7所示。

图7 参数优化过程曲线Fig.7 Parameter optimization process curves

最优参数结果如下：二次侧电压V2为950.6 V，二次侧电阻R2为0.3 Ω，二次侧电感L2标幺值为0.518 5。采用优化后的变压器模型参数，选取同样10次试验数据，与仿真数据对比，经过定量仿真可信度分析，结果如表2所示。其可信度为

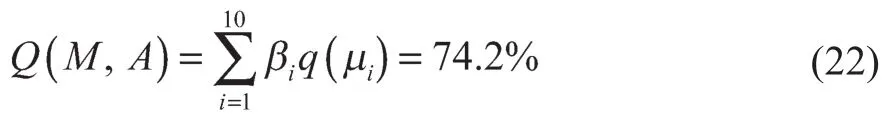
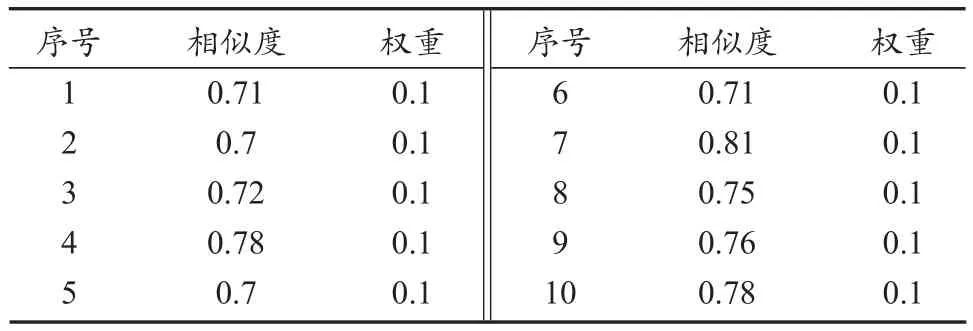
表2 参数优化后，试验数据与仿真数据相似度分析Tab.2 Similarity evaluation of test data and simulation data after parameter optimization

选取图6中的试验数据与由优化后的参数计算出的仿真结果进行对比（图8）。可以看出，优化后的仿真数据明显与试验数据更加吻合，可信度大幅提升，定量分析与定性分析结论一致。

图8 参数优化后，试验数据及仿真数据对比Fig.8 Comparison between measured data and simulated data after parameter optimization

4 结语

本文搭建了牵引变压器仿真模型，通过选择仿真可信度作为优化目标函数、选择输入信号及高敏感关键参数，进行了参数优化计算。无论是定量分析还是定性分析结果均显示，模型参数优化后，仿真系统可信度都大幅提高。本文所设计的优化过程为通用方法，其同样可移植至其他模型用于参数优化，由此实现使整个仿真系统可信度提升的最终目标。本文中参数优化的约束条件是根据经验设置的，后续将根据应用情况选择实际的约束范围开展参数优化研究。