基于双雷达的轨道交通测速方法及误差分析

周 媛，周巧莲，郑成鑫，张谦虓

（1.上海申通地铁集团有限公司，上海 201103；2.上海无线电设备研究所，上海 201109）

0 引言

轨道交通测速传感器是控车系统的核心设备之一，其所获取的高精度列车速度信息是车辆安全运行的前提和保证[1-2]。轨道交通测速主要有地感线圈测速、转动测速、视频测速、GPS定位测速、激光测速和雷达测速等方式。地感线圈的安装和维修会对地面造成破坏[3]，转动测速在车轮打滑、空转时测速精度低[4]，视频测速存在监控范围有限的问题[5]，GPS定位测速有分辨率低、在山区或隧道等存在信号盲区的缺点[6]，激光测速对环境适应性差[7-8]，而雷达测速具有受环境影响小、精度高的优势，是目前比较主流的测速方法。传统的单部雷达测速需要精确的雷达天线相位中心高度信息，而雷达天线相位中心与天线几何中心一般不重合，这给雷达高度测量带来了困难。朱燕、刘逸通在多普勒效应原理的基础上，利用Burg算法提高测速精度[9]，但是实现算法需要迭代计算，时间复杂度高；陈红江、张浩等提出了一种双雷达天线测速方法，其基于非对称发射角的双天线雷达，以不同的频率发射雷达波，并利用多普勒效应相关算法进行解析计算[10]，但是双频增加了测速系统复杂度。为此，本文提出了一种双雷达联合计算列车速度的方法，其计算方法和系统设计简单、可靠性高。文中对双雷达测速技术误差原理进行了分析，并采用目前轨道交通高精度激光测速设备进行了对比测试验证。

1 双雷达联合测速原理

基于多普勒效应的测速雷达被安装在列车底部，雷达天线向轨面发射电磁波，电磁波经过轨面反射回天线。雷达随机车相对轨面的运动会使得发射波和接收波之间存在一定的频率差，即多普勒频率。图1示出雷达测速示意，其中，H为雷达高度，R为斜距，VH为列车相对于轨面的运行速度，φ为雷达斜视角，Vr为雷达相对于轨面的径向运行速度。

由雷达和轨面之间相对运动而产生的多普勒频率[11-13]计算如下：

式中：λ——雷达波长。

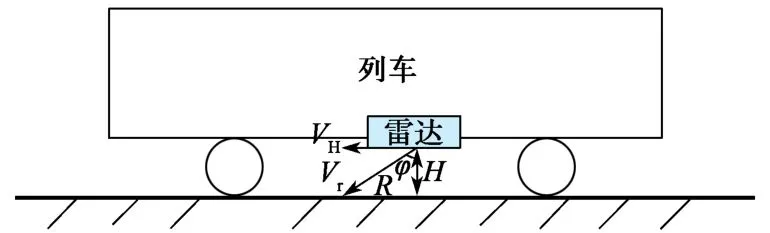
图1 雷达测速示意Fig.1 Schematic diagram of radar velocity measurement

1.1 单雷达测速

单部雷达测速的方法如下：

（1）对回波数据进行二维快速傅立叶变换（fast Fourier transform，FFT）处理，从而获取二维图像；

（2）提取图像中最强散射点，获取其所在距离门，并计算斜距R；

（3）利用最强散射点所在距离门的回波数据估计其所对应的多普勒频率fd；

（4）根据式(2)解算列车速度VH。

单部雷达测速需要首先测量得到精确的雷达高度H，但是雷达天线相位中心通常不是天线的几何中心，这给单部雷达测速的工程应用实现带来了困难。

1.2 双雷达测速

图2示出两部雷达联合测速几何关系。假设存在安装高度位置不同的两部雷达（简称“低雷达”和“高雷达”），其高度分别为H1和H2。利用1.1节所述单部雷达测速的方法，计算得到低雷达的斜距为R1，多普勒频率为fd1；高雷达的斜距为R2，多普勒频率为fd2。

图2 两部雷达联合测速几何关系Fig.2 Geometrical relationship of two-radar velocity measurement method

根据图2所示的几何关系，可以得到两个多普勒方程：

式中：φ1——低雷达斜视角；φ2——高雷达斜视角。

假设两部雷达高度差(ΔH=H2-H1)已知，则式(4)可以表示为

由于双雷达测量时速度相同，联立式(3)和式(5)，可以得到

通过求解式(6)，即可得到低雷达的高度H1，进而得到高雷达的高度H2。将解算得到的雷达绝对高度代入式(3)和式(4)即可解算列车速度。需要说明的是，利用双雷达联合估计雷达高度，在列车静止时，式(6)变为恒等式，无法解算雷达高度。此外，由于双雷达估计的斜距和多普勒频率均存在误差，导致单次解算雷达高度精度较低。在实际处理过程中，利用多次解算结果进行平均处理，并通过固定间隔时间更新雷达高度，以此提高测算精度。

解算得到两部雷达的高度后，可以通过两种方法估计列车速度：如果两部雷达都没有损坏，则根据式(2)和式(3)分别估计列车速度，然后对获得的两个速度估计值进行加权平均得到列车估计速度；如果其中一部雷达损坏，则利用另一部雷达估计列车速度。

利用双雷达联合测速技术，不需要测量单部雷达的高度，仅需要测量两部雷达之间的高度差，工程可实现性更高。

2 雷达测速技术误差分析

根据第1节介绍的双雷达测速原理，其误差因素包括多普勒频率估计误差、雷达斜距估计误差、雷达高度误差和雷达垂直向速度误差4个方面。

本文的误差分析和工程试验采用同样的参数设置，具体如下：雷达工作在K波段、载频波长为1.25 cm，最大调频率带宽为500 MHz，对应的距离分辨率为0.3 m；H1=0.894 m，H2=0.960 m，ΔH=0.066 m，φ1=60°，φ2=70°。

根据式(2)可知，多普勒频率估计误差Δfd与其产生的雷达测速误差ΔV之间的关系为

根据式(7)可知，当单部雷达斜视角不变时，雷达测速误差ΔV与多普勒估计误差Δfd成正比关系。两部雷达中，斜视角φ较小的雷达其测速精度受多普勒估计误差的影响更大。图3示出本文仿真参数下双雷达多普勒频率估计误差导致的雷达测速误差。可以看出，对于单部雷达而言，其测速误差与多普勒频率估计误差成正比关系，相同Δfd对应的低雷达测速误差大于高雷达的；综合φ1和φ2参数设置可知，斜视角较小的低雷达测速精度受Δfd的影响更大。

图3 多普勒频率估计误差导致的测速误差Fig.3 Velocity measurement error caused by Doppler frequency estimation error

根据式(6)，斜距误差会使计算得到的H产生误差。根据式(3)，ΔH和斜距误差ΔR都会使测量速度产生误差。以下利用上述仿真参数分析斜距估计误差对雷达测速误差的影响。图4示出雷达的ΔR导致的测速误差曲线，可以看出，ΔV随着ΔR的增大而增大，且低雷达测速精度受ΔR的影响更大。

图4 斜距估计误差导致的测速误差Fig.4 Velocity measurement error caused by slant distance estimation error

在数据处理过程中，固定间隔时间，利用双雷达解算雷达高度，得到的雷达高度用来计算并更新列车速度。在间隔时间内，其利用同一个高度解算列车速度。但是在列车运行过程中，雷达会存在抖动现象，使计算速度所用雷达高度产生误差。图5示出雷达高度误差导致的测速误差。可以看出，测量速度误差随雷达高度误差的增加而增加，且低雷达的测速精度受高度误差的影响更大。

图5 高度误差导致的测速误差Fig.5 Velocity measurement error caused by height estimation error

式(3)和式(4)是基于雷达运动速度方向与轨面平行工况，然而在列车实际运行过程中，列车颠簸会使雷达产生垂直方向速度。如图6所示，假设列车颠簸引起的垂直方向速度为Vr，列车沿水平方向的速度为VH，二者合成的速度为V。由于从雷达回波数据估计的多普勒频率为合成速度V引起的多普勒频率，使雷达最终测得的速度为V，与速度VH间存在一定的误差。

图6 列车垂直向速度对测速精度的影响示意Fig.6 Diagram of influence of vertical train speed on velocity measurement accuracy

综上分析可知，雷达垂直方向速度同样会导致测速误差，两者的关系如图7所示。可以看出，雷达垂直方向速度越大，测量速度误差越大，且低雷达测速精度受垂直方向速度影响更大。

图7 雷达垂直方向速度导致的测速误差Fig.7 Velocity measurement error caused by radar vertical speed

3 工程试验结果

由于目前成熟的高精度轨道交通车辆测速设备主要采用轴端测速和激光雷达测速两种方式，其中，激光测速产品以其高精度测速特征已在国外高速铁路上有大规模应用，因此本文采用激光测速设备哈斯勒作为对标设备进行功能和测速精度的初步验证。哈斯勒是目前市场上主流列车测速产品中测速精度最高的测速设备，其在列车速度小于100 km/h时测速精度达0.2 km/h，列车速度大于100 km/h时测速精度小于列车速度的0.2%。但该产品由于国外技术垄断，市场价格较高。

基于双雷达测速技术制造的测速雷达样机被安装在上海申通地铁张江试验线试验车上，并分别针对列车最高速度60 km/h和最高速度80 km/h、加速段和减速段、60 km/h惰行段和80 km/h惰行段等几种工况展开了多批次测试。在测速列车上同时还装备了高精度激光测速设备哈斯勒（两设备性能指标对比如表1所示）。将双雷达测速结果与高精度激光测速结果进行对比，以验证双雷达测速技术的测速精度和稳定性，其中采集数据点的间隔时间为40 ms。

表1 试验设备性能指标对比Tab.1 Comparison of performance indexes of experimental equipment

图8示出列车从静止状态开始启动、到基本维持匀速运动、最高速度达60 km/h、再到制动至停车的过程中，雷达测速结果与激光测速结果的对比。可以看出，雷达测速曲线与激光测速曲线基本吻合。

图8 最大速度60 km/h雷达与激光测量结果对比Fig.8 Comparison between radar and laser velocity measurement results at the maximum speed of 60 km/h

图9示出列车从静止状态加速到最大速度为80 km/h、再到制动至停车过程中，雷达测速结果与激光测速结果对比。可以看出，该过程中雷达测速结果与激光测速结果也基本一致。

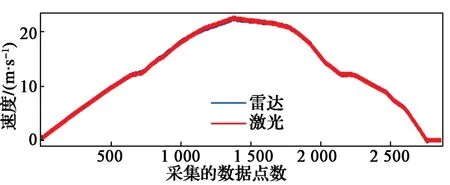
图9 最大速度80 km/h时，雷达与激光测量结果对比Fig.9 Comparison between radar and laser velocity measurement results at the maximum speed of 80 km/h

图10示出列车在加速运行阶段雷达测速结果与激光测速结果对比。可以看出，该阶段雷达测速结果与激光测速结果基本吻合，且雷达测速数据波动更小。

图10 加速段测量结果对比Fig.10 Comparison of velocity measurements in the acceleration section

图11示出列车在减速运行阶段，雷达测速结果与激光测速结果对比。可以看出，该阶段雷达测量结果与激光测量结果基本吻合，且雷达测速数据波动更小。

图11 减速段测量结果对比Fig.11 Comparison of velocity measurement results in the deceleration section

图12和图13分别示出列车在60 km/h及80 km/h惰行阶段雷达测速结果与激光测速结果。可以看出，在惰行阶段，二者基本吻合，且雷达测速数据的波动明显小于激光测速数据的。

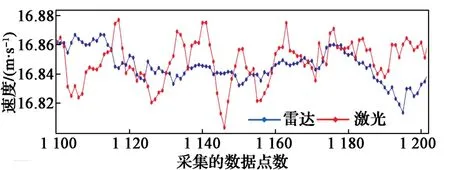
图12 60 km/h惰行段测量结果对比Fig.12 Comparison of velocity measurement results in 60 km/h idle section

图13 80 km/h惰行段测量结果对比Fig.13 Comparison of velocity measurement results in 80 km/h idle section

综上分析可知，双雷达系统测速精度与高精度激光测速精度相当，且测速稳定。此前列车高精度激光测速产品均需从国外进口，且价格较高。通过对比测试可以看出，本文所提双雷达测速系统其功能和测速精度指标与进口激光测速产品的相当，且成本不到激光测速产品的一半。

4 结语

本文提出一种双雷达测速的计算方法，工程测试结果验证了该方法的有效性。所提双雷达测速技术具备工程化应用基础条件，不仅可靠性高，即使一部雷达发生故障，另一部也可以单独完成测速工作；而且还具有精度高的优势，在某些测试工况下测速精度甚至高于激光测速的。后续将通过设计试验、型式试验等多种方式来进一步优化其精度、性能指标及工程化应用技术。