牵引计算在轨道交通特定项目中的应用及研究

杨海鹏，薛巧丽

（湖南中车时代通信信号有限公司 北京分公司，北京 100079）

0 引言

在城市轨道交通信号系统实施过程中，行车间隔和系统运营能力是衡量系统能力的关键指标之一，是最终用户考核和运营验收系统的关键参考依据，也是信号系统设计重点关注的内容。因此，在信号系统工程设计初期，通过列车牵引计算仿真的手段，对系统运营能力和行车间隔进行计算，并验证能否满足最终用户需求，是一种有效的论证方法。

本文以特定项目——长沙轨道交通3号线（简称“3号线”）为例，具体介绍牵引计算方案。3号线一期工程信号系统工程范围为：全长36.398 km的正线及辅助线路、25座正线车站、1个车辆段（洋湖垸）、1个停车场（张公塘）、34列初期配属车。

针对3号线既定现场条件，通过牵引计算[1]对不同场景下的系统能力进行充分论证，从而确认系统运营能力满足用户要求。

1 牵引计算仿真参数设计

列车牵引计算仿真是根据物理学原理、结合车辆特性参数及实际应用经验积累，基于实际线路条件，模拟仿真列车运动的计算方法。

列车运行仿真主要依赖于列车特性参数（Jerk值、梯度加速度、常用制动减速率等）、线路特性参数（限速、坡度、长短链、站停时间等）、折返配置参数、信号系统反应时间等，任何输入参数变动，都会影响模拟仿真结果。因此牵引计算仿真基于以下假设条件：

（1）线路数据输入正确，包括站台位置、坡度及限速等；

（2）列车参数输入正确，包括列车车重、车长、牵引特性、电制动特性；

（3）列车质量在整个运行过程中保持不变；

（4）线路轨面条件良好，可提供列车牵引所需要的黏着系数。

1.1 列车特性参数

牵引计算所需列车特性参数主要包括车辆参数、牵引制动参数和梯度加速度等。

表1示出牵引计算过程中所用到的车辆主要参数，包括车辆长度、编组和重量等。

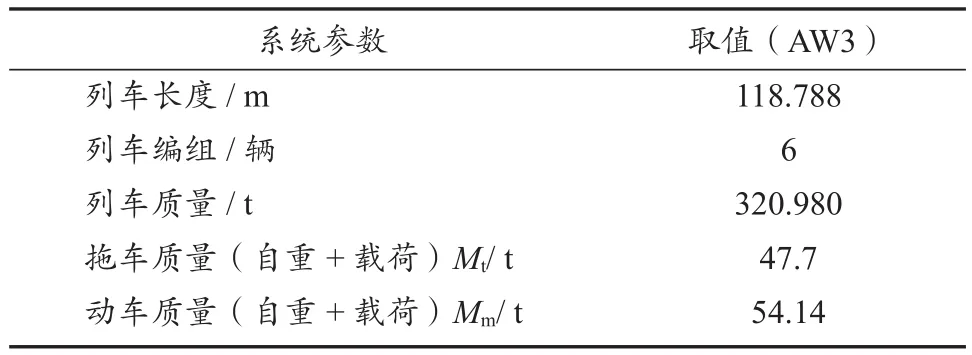
表1 车辆参数Tab.1 Vehicle parameters

表2示出牵引计算过程中所用到的列车牵引制动参数（含最大加速度、Jerk值等），其中GEBR（guaranteed emergency brake rate）为最不利条件下的紧急制动率；EB（emergency braking）为紧急制动。

表2 列车牵引制动参数Tab.2 Train traction and braking related parameters

表3示出牵引计算过程中所用的列车梯度加速度参数，列车在不同速度下的加速度信息不同。

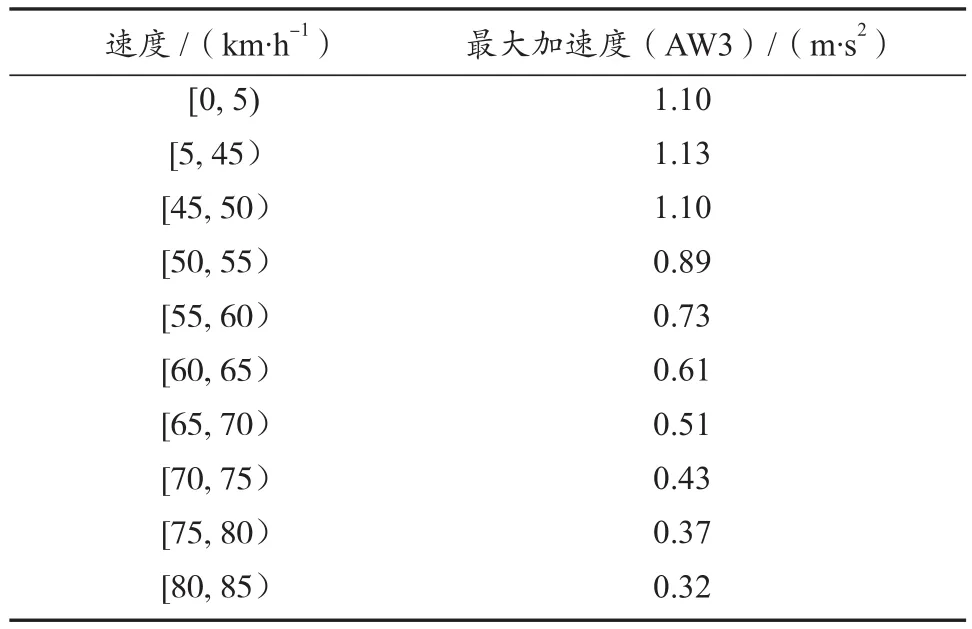
表3 列车梯度加速度参数Tab.3 Train gradient acceleration parameter

1.2 线路特性参数

牵引计算所需线路特性参数主要包括限速、坡度及长短链等。

线路限速信息如表4所示，其用于限制列车的顶棚速度。正线最高限速（含正向道岔）85 km/h，站台最高限速60 km/h，侧向道岔最高限速35 km/h。

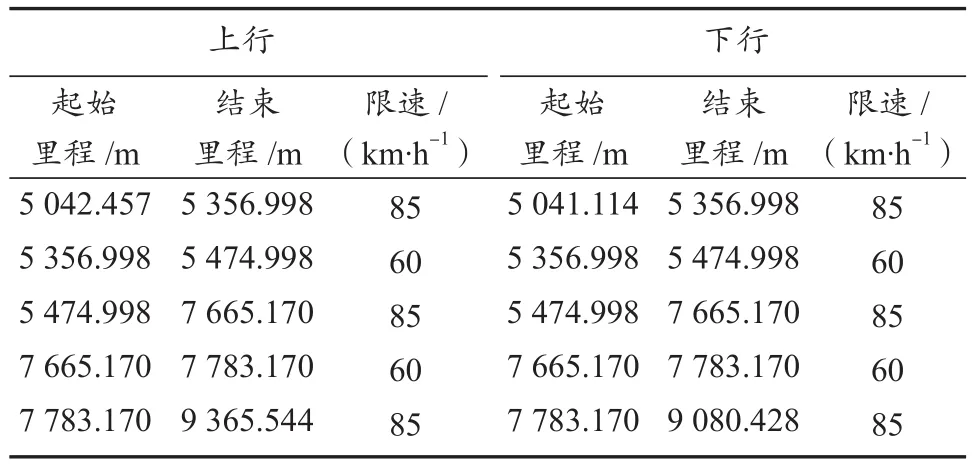
表4 限速信息Tab.4 Speed limit information

线路坡度信息如表5所示，其用于计算变化的加速度。

表5 坡度信息Tab.5 Slope information

线路长短链信息如表6所示，其用于线路位置信息转换。旧里程代表长短链的起始里程，新里程代表长短链的终止里程。

表6 长短链信息Tab.6 Long and short linked information

2 牵引计算系统结构

牵引计算系统结构主要由列车运行控制模型、安全制动模型、行车间隔计算模块、折返能力计算模块组成。

2.1 列车运行控制模型

为保证仿真模拟效果更贴近于真实情况，列车运行控制模型[2-5]考虑了Jerk值（纵向冲击率）、阻力、坡度等多种因素。列车运行控制主要分为牵引、惰行、制动3个阶段，列车状态在这3个阶段中转换，从而得到列车运行曲线[6-8]。

（1）牵引阶段。当列车速度低于当前限速时，列车需牵引加速。考虑到旅客舒适度以及列车实际牵引过程，列车不是直接以最大加速度进行加速，而是考虑Jerk值进行逐步迭代而增加至最大加速度。列车能达到的最大加速度是与速度相关的变量，在不同的运行速度下列车牵引时可提供的最大加速度值不同，具体因不同的车辆而异，由车辆系统提供分梯度的加速度列表。

（2）惰行阶段。当列车速度达到当前限速范围、且其指导曲线处于平直段时，出于节能考虑，列车进入惰行阶段。列车当前速度一旦达到惰行速度阈值，列车状态即转为惰行；随着摩擦阻力、基本阻力、坡度等因素影响，列车速度逐渐降低，其速度一旦低于启动速度阈值，列车即转为牵引状态。列车状态在惰行和牵引状态间来回切换，从而使得列车速度围绕着指导速度曲线上下波动。

（3）制动阶段。当列车速度高于当前限速时，列车需要进行制动减速。考虑到旅客舒适度及列车实际制动过程，列车不是直接以常用减速度直接进行减速，而是根据其当前状态及Jerk值进行逐步迭代而增加至常用减速度。在制动过程中，列车速度若远低于当前限速，则需及时调整至牵引状态。

列车运行过程可用由速度和位置组成的二维曲线表示，称为列车运行曲线（图1）。

图1 列车运行曲线Fig.1 Train running profile

2.2 安全制动模型

国际标准IEEE 1474.1—2004《基于通信的列车控制（CBTC）系统的性能和功能要求》给出了CBTC系统推荐的典型安全制动模型（图2）[9]。该模型考虑了线路、信号、车辆等各种安全相关的因素，是进行安全制动距离计算的依据。

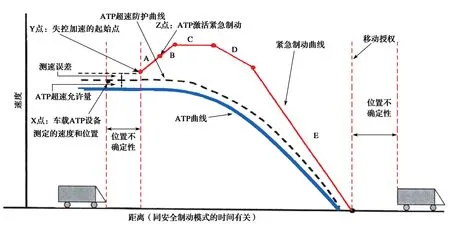
图2 CBTC系统安全制动模型Fig.2 Safe braking model of CBTC system

列车施加紧急制动停车的过程需要考虑雨、雪、冰等不利环境条件下可能达到的最小黏着，考虑可接受的制动系统失效及载重情况[10]的最不利条件，从而保证列车在最不利[条件下的安全运行。图2给出了列车在最不利情况下进行紧急制动过程的5个阶段：

（1）A阶段为信号系统反应阶段，是列车超速到车载ATP系统给出紧急制动命令的阶段，其间列车仍然以原加速度加速运行。

（2）B阶段为牵引力切除阶段，是牵引系统从最大加速度减小到0（牵引力完全切除）的过渡阶段。为计算最不利情况，假设其间列车仍然是以原加速度加速运行。

（3）C阶段为牵引力切除到制动力施加的延迟阶段，是制动系统从接收制动命令到施加制动动作的制动系统反应阶段，此时列车牵引力已经被切除，而制动力尚未实施。为计算最不利情况，假设其间列车仍然保持原速度匀速运动。

（4）D阶段为制动建立阶段，是制动系统从开始制动、制动减速度从0到最大值（制动力达到90%）的制动建立阶段。为计算最不利情况，假设其间列车仍然保持原速度匀速运动。

（5）E阶段为以可保证的紧急制动减速率（GEBR）减速到停车阶段，是制动系统从充分实施紧急制动开始到列车减速到0的制动阶段。

由于列车设备的参数误差以及列车位置的不确定性等因素，本模型采用安全裕量的方式对其进行补偿。因此，在最不利条件下，列车在线路某位置上的停车距离为

式中：Vcur——列车超速前的当前速度，m/s；acur——列车超速前的当前加速度，m/s2；Vafter-acc——列车加速后的速度，m/s；Vend——制动时间后列车运行的最终速度，取值为0，m/s；aGEBR——紧急制动减速率，m/s2；tA,tB,tC,tD,tE——列车紧急制动过程中各阶段所对应的时间，s；SA,SB,SC,SD,SE——列车紧急制动过程中各阶段所经过的距离，m；Smargin——安全制动距离中的安全裕量，经验取值为总距离的30%，m；Ssafe——最终计算所得的安全制动距离，m。

2.3 行车间隔计算模块

行车间隔计算依赖于列车控制模式，本节分别给出不同列车控制模式下的计算过程。

2.3.1 CBTC模式

列车CBTC模式下，移动授权必须小于该位置在最不利情况下的列车安全制动距离。连续列车追踪距离是由当前位置在最不利情况下的后车制动距离、前车位置的不确定性、列车车长等因素决定的。因此，CBTC模式行车间隔是指前车不影响后车运行情况下，前后车连续通过同一位置时的最小时间间隔。图3示出在CBTC模式下的行车间隔计算过程。

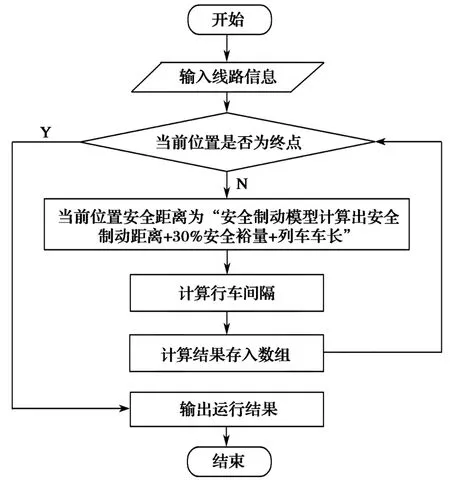
图3 CBTC模式行车间隔计算Fig.3 Headway calculation in CBTC mode

2.3.2 后备模式

后备模式下，计轴区段的占用空闲代表列车位置，同一时间同一区段仅允许一列车经过。为保证安全，前后车之间至少间隔两个物理区段。因此后备模式下同一位置的最小行车间隔指前车经过该位置出清前面2个区段后与后车经过该位置的时间差。图4示出在后备模式下的计算过程。

2.4 折返能力计算模块

线路折返通常考虑的是列车在折返路径上的运行时间，但缺乏与上下站间运营衔接方面的考虑。因此，本文在常规折返时间计算算法基础上，增加了与上下站间行车间隔方面的考虑。

首先将折返路径拉直看作直线，计算3站2区间内的行车间隔，然后计算折返路径上的理论折返时间，最后将两者进行比较。若行车间隔瓶颈点在折返区间，且理论折返时间大于行车间隔值，则取理论折返时间；若行车间隔瓶颈点不在折返区间，理论折返时间大于行车间隔值，则取理论折返时间；若行车间隔瓶颈点不在折返区间，但是理论折返时间小于行车间隔值，则取行车间隔值。

2.4.1 站前折返

站前折返为列车未进站之前进行折返的运行轨迹。选取两个车站作为示例进行描述（图5），该路径采取阳光站下行出站S处作为站前折返的起点，经过E点折返到山塘站上行站台，途经A和C计轴点后到达阳光站上行站台。

图5 站前折返Fig.5 Turn back before station

列车从折返进路E点出发，默认进路已经办理好，不需要单独考虑进路办理时间。当列车运行出清A计轴点处，列车进站对标停车停站换端。列车进站过程与折入进路取消、折出进路办理、道岔扳至定位同时进行，列车停站过程中同时进行换端。因此该处所用时间应该取(t2×2+tdwell)与（tswitch+tcancel_route+tset_route）中较大值。列车在出清C计轴点后，进路取消，进路办理，道岔开始被扳动到反位，待道岔扳动到位后，下一列车可以发车。

因此该算法中CBTC模式下折返间隔时间为

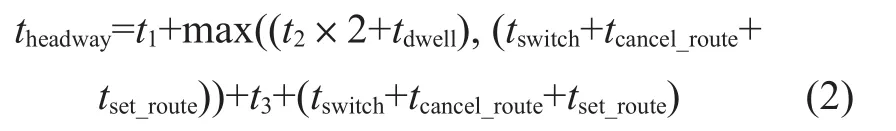
式中：t1——列车从E点出发到出清A计轴点时间；t2——从列车尾部过A计轴点到列车在山塘站停稳时间；tdwell——列车在山塘站上行站台停站时间；t3——列车从A计轴点出发到出清C计轴点时间；tswitch——道岔扳动时间,进路中每增加一组道岔，扳动时间错峰1 s；tcancel_route——进路取消时间；tset_route——进路办理时间。

2.4.2 站后折返

站后折返为列车进站之后进行折返的运行轨迹。选取两个车站作为示例进行描述（图6），该路径采取阳光站上行出站S处作为站后折返的起点，列车运行到山塘站经E折返到折返轨，换端后途经A和C计轴点到达山塘站下行站台，然后再行驶到阳光站下行站台。

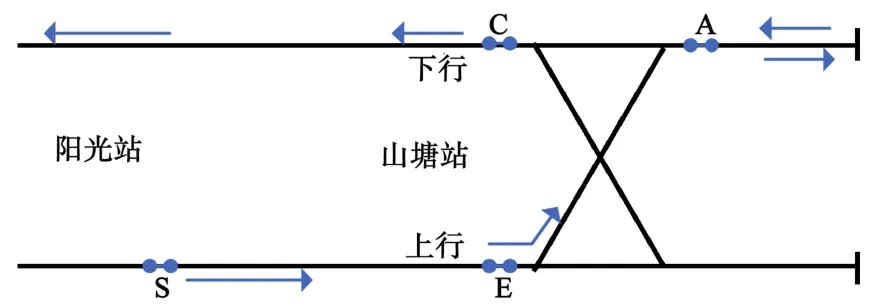
图6 站后折返Fig.6 Turn back after station

列车从上行E处出发时，默认进路已经办理好，不需要单独考虑进路办理时间。当列车运行出清A计轴点之后，列车开始换端准备折返。因列车换端时间与折入进路取消、折出进路办理、道岔扳至定位同时进行，因此取tb与（tswitch+tcancel_route+tset_route）二者中较大值。列车在出清C计轴点后，另外一辆车的折入进路开始办理；待进路办理好后，下一列车可以从上行E点出发。

因此该算法中CBTC模式下折返间隔时间为

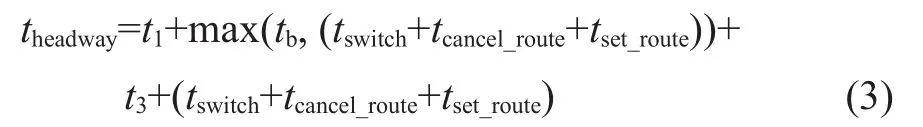
式中：tb——列车在折返轨换端时间。

3 仿真计算结果及分析

根据第2节所述，针对特定运行路径提供系统运营能力及行车间隔计算。图7、图8分别为列车运行曲线和行车间隔曲线，其中黄色字符串代表相应站台名称。表7的计算结果包含旅行时间、旅行速度及行车间隔等。

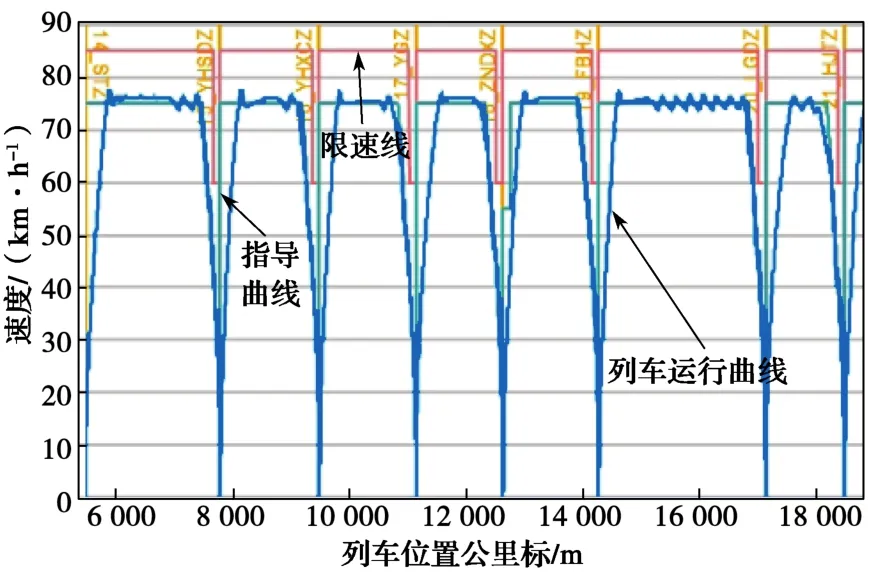
图7 列车运行曲线Fig.7 Train running profile

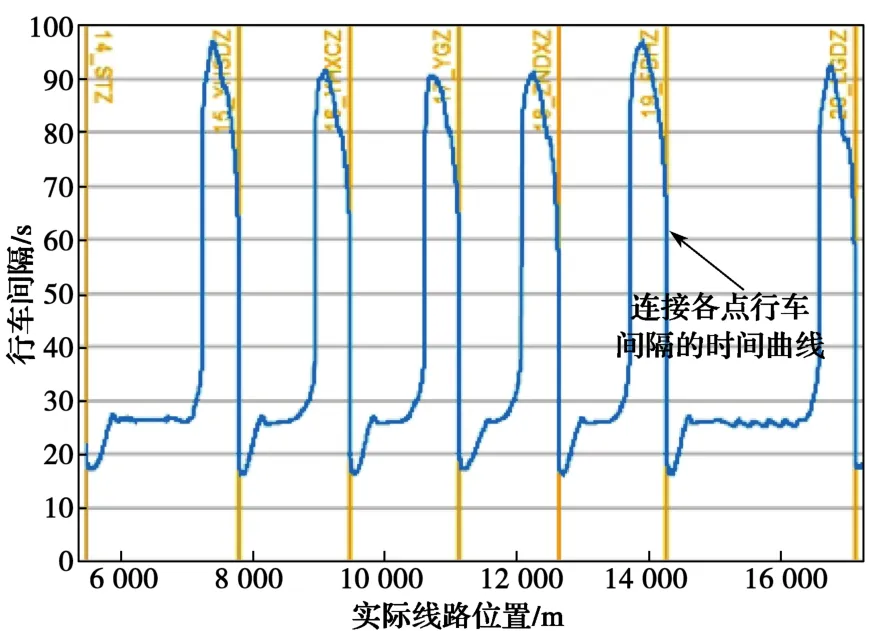
图8 行车间隔曲线Fig.8 Headway profile

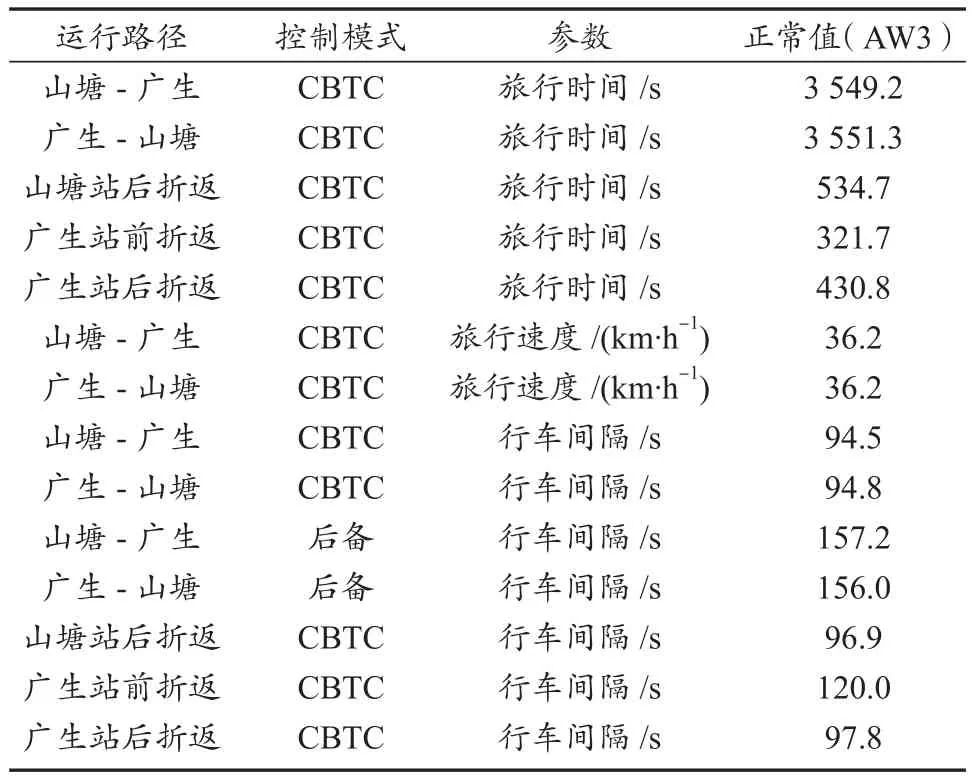
表7 计算结果Tab.7 Calculation results

由表7可知，行车间隔及折返能力可以满足在CBTC模式下不超过2 min、在后备模式下不超过5 min的要求。

4 结语

城市轨道交通列车的牵引/制动计算过程是一个复杂的、非线性的过程[11]。本文借助牵引计算系统，实现了列车牵引/制动特性曲线的模拟。目前，该系统已在多个工程项目中进行了应用。实践证明，通过牵引计算系统计算可对系统运营能力是否达到预期效果给出直观的判断，对于信号系统的优化设计具有很好的指导意义。

目前，若有不满足系统运营能力要求的位置，可通过牵引计算系统识别出来，通过系统优化设计，可使系统运营能力满足要求。但牵引计算系统应具备自动生成符合系统运营能力的设计方案，后续将在这方面做进一步的研究工作。