考虑应力三轴度影响的30Cr MnSiNi2A 钢韧性断裂研究*

余万千，郁 锐，崔世堂

（1.西安现代控制技术研究所，陕西 西安710065；2.中国科学技术大学近代力学系中科院材料力学行为和设计重点实验室，安徽 合肥230027）

30CrMnSiNi2A 钢是一种低合金高强度钢，由于综合力学性能良好而且原材料和加工成本相对较低，被广泛应用于侵彻/穿甲战斗部壳体、飞机起落架和发动机壳体等零部件的制造。这类结构在工作时经常受到较高的静态和动态载荷，对材料屈服强度和韧性断裂等力学性能的研究在相关工程设计中非常关键。其研究大致从微观和宏观两方面进行，微观方面主要研究裂纹产生的机理以及裂纹扩展所遵循的物理条件，宏观方面主要探索材料发生断裂时各个力学量之间的关系，即断裂准则。目前有限元模拟分析成为工程结构强度评估的重要手段之一，选择合适的断裂准则是提高数值模型预测能力的关键，因此研究30CrMnSiNi2A 钢的韧性断裂特性有着广阔的实用价值。

Johnson-Cook 失效模型综合考虑了应力三轴度、应变率和温度对材料力学性能的影响，其方程形式简单，参数容易标定，被广泛应用于冲击动力学领域。武海军等[1]、周义清等[2]研究了30CrMnSiNi2A 钢在不同应变率下的塑性流动特性，确定了常温Johnson-Cook 本构模型参数。李磊等[3]研究了应力三轴度大于1/3时的材料断裂行为，并拟合了常温下30CrMnSiNi2A 钢的Johnson-Cook 本构模型和失效模型参数。目前的研究主要集中在应变率对力学性能的影响，缺少对不同温度和大范围应力三轴度下30CrMnSiNi2A 钢韧性断裂的探讨。

研究表明，金属的韧性断裂与应力状态、应变率和温度等因素相关[4-6]。应力三轴度定义为平均应力和等效应力之比，通常用来表示结构一点处的应力状态。Johnson-Cook 失效模型中采用一个单调函数描述应力三轴度对断裂应变的影响。Bao等[7]对2024-T351铝合金进行了一系列试验，确定了从负向到正向全区段内应力三轴度与断裂应变的关系曲线，发现不同失效模式下曲线走势不同。李营等[8]、张朴等[9]发现船用低碳钢的断裂应变与应力状态密切相关，且在不同的应力三轴度区间差异较大。桂良进等[10]研究了不同三轴应力状态下先进高强钢的失效特性，通过数值计算发现Bao-Wierzbicki 失效模型预测能力在低应力三轴度情形下较好。鉴于此，采用Johnson-Cook 失效模型将缺口拉伸试样结果外推至其他应力状态，值得商榷。

为了较全面地研究30CrMnSiNi2A 钢的韧性断裂，本文中基于Johnson-Cook 本构模型和失效模型，引入Bao-Wierzbicki 失效模型对应力三轴度的考虑，设计开展不同温度下的准静态、动态拉伸、剪切和压缩试验，结合有限元模拟分析，确定一套适用于30CrMnSiNi2A 钢的本构和失效参数。

1 参数标定方法和试验设计

采用试验和数值模拟结合的方法研究30CrMnSiNi2A 钢的韧性断裂，标定Johnson-Cook 模型和Bao-Wierzbicki 模型参数，具体方法如下：

（1）设计加工拉伸、剪切和压缩试件，开展一系列准静态、动态试验，获得载荷-位移曲线，记录失效位置和对应的位移；

（2）建立光滑圆棒拉伸试验的有限元模拟模型，通过迭代获得真实应力-真实应变曲线，拟合出Johnson-Cook 本构模型参数；

（3）利用有限元法计算不同试件失效位置的等效塑性应变和应力三轴度变化曲线；

（4）确定不同试件的平均应力三轴度和断裂应变，拟合出Johnson-Cook 失效模型和Bao-Wierzbicki失效模型[11]参数。

准静态拉伸和压缩试验采用MTS-809材料试验机，应变率为0.001 s−1，光滑圆棒试件尺寸和数据处理方法依据为GB/T 228.1—2010《金属材料拉伸试验第1部分：室温试验方法》和GB/T 228.2—2015《金属材料拉伸试验第2部分：高温试验方法》，试验中采用引伸计精确测量试件标距段的应变，开展了298、473、773 K 这3种温度下的测试。动态拉伸试验在套筒式霍普金森拉杆上完成，开展了1 000、2 000、4 000 s−1这3种应变率下的试验。为了获得不同的应力状态，除了光滑圆棒试件外，本文中共设计了6组异形试件，详见表1和图1。

30CrMnSiNi2A 钢化学组分如表2所示，试件按照某侵彻爆破战斗部壳体技术要求进行热处理。

表1 异形试件Table 1 Abnormal specimens

图1 异形试件尺寸（单位：mm）Fig.1 Dimensions of abnormal specimens (unit:mm)

表2 30Cr MnSiNi2A 钢的化学成分(质量分数，%)Table2 Composition of 30Cr MnSiNi2A steel (mass fraction,%)

2 本构模型参数标定

Johnson-Cook 本构模型表达式如下：

式中：σe为流动应力；εep为等效塑性应变；ε ˙∗=ε˙ep/ε˙0为无量纲等效塑性应变率，ε ˙ep为等效塑性应变率，ε˙0为参考应变率；T*=(T−Tr)/(Tm−Tr)为无量纲温度，T 为材料温度，Tr为参考温度，Tm为材料熔点；A、B、n、C、m为待定系数。

A、B、n可通过在参考应变率（准静态试验应变率）和参考温度（室温）下的光滑圆棒拉伸试验结果获得。在此条件下，本构模型可简化为：

当等效塑性应变为零时，A=σe即为材料屈服时的真实应力。对式（2）进行变换：

采用最小二乘法对真实应力-真实应变曲线拟合即可确定B 和n。颈缩之前，通过简单的数学变换就可将工程应力-工程应变曲线转换为真实应力-真实应变曲线。颈缩之后，采用ABAQUS软件输入应力应变曲线，通过不断地迭代修正应力应变关系，比对载荷-位移曲线，最终得到完整的真实应力-真实应变曲线。将模型中各项解耦，通过类似的最小二乘拟合可以确定C 和m。

图2是高温下的光滑圆棒准静态拉伸应力应变曲线，其中5-1、5-2和5-3号试验温度为473 K，6-1和6-2号试验温度为773 K，可以看出两种温度下的试验重复性较好，试验结果可靠。图2中5-1和5-3号曲线对应的试件断裂位置靠近标距段边缘，因此断裂应变测量存在误差，5-2号曲线对应的试件断裂位置在试件中心，本文中以此为参照开展数值模拟。

表3列出了不同温度和应变率下材料的屈服应力，按上述方法拟合，30Cr MnSiNi2A 钢Johnson-Cook 本构模型参数A=1 163 MPa，B=753.4 MPa，n=0.4509，C=0.0648，m=1.53。采用该模型对298 K 温度下的光滑圆棒准静态拉伸试验进行数值模拟，图3比较了载荷-位移曲线的试验值和模拟值，两者符合较好。

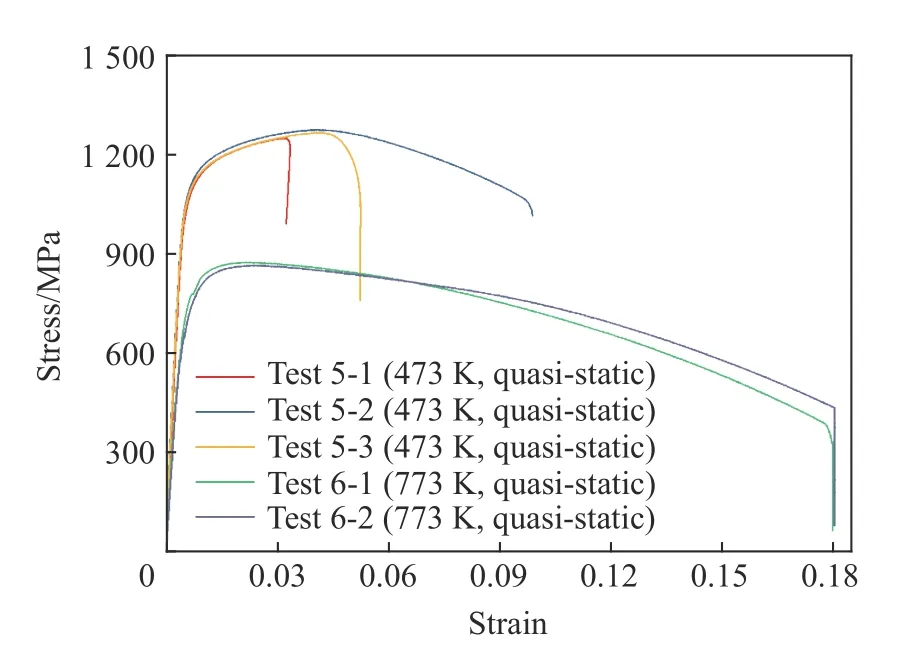
图2 高温下的应力应变曲线Fig.2 Stress-strain curves at different temperatures

表3 光滑圆棒试件的屈服应力和断裂应变Table 3 Yield strength and fracture strain of round bars

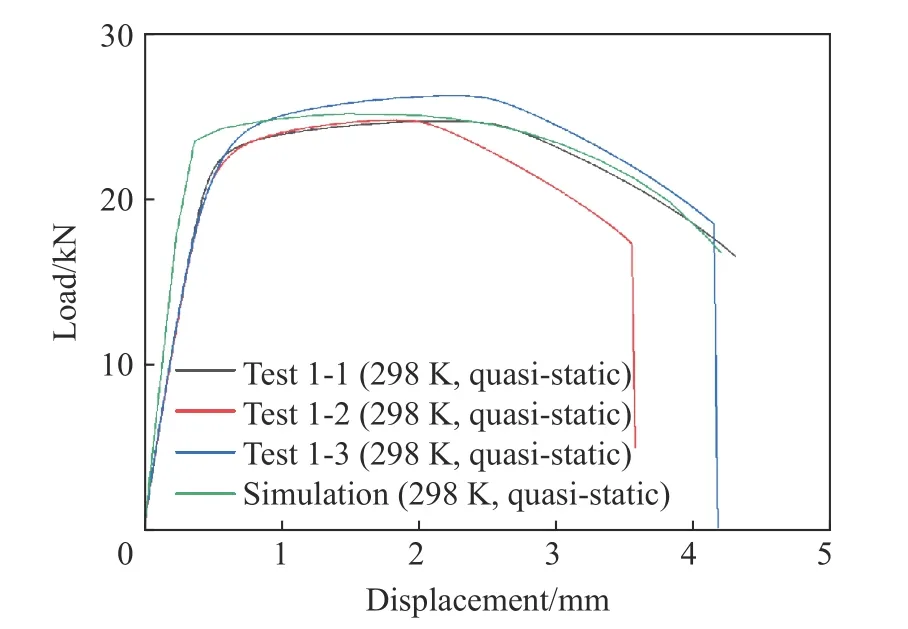
图3 载荷-位移曲线模拟值与试验值比较Fig.3 Comparison of load-displacement curves between simulation and test

3 失效模型参数标定

首先采用Johnson-Cook 失效模型描述应变率和温度对断裂的影响，然后比较Johnson-Cook 和Bao-Wierzbicki 失效模型对不同应力状态下材料韧性断裂的预测能力。

Johnson-Cook 失效模型表达式如下：

式中：εf为等效塑性断裂应变，σ*=p/σeq=−η，p为静水压力，σeq为等效应力，η为应力三轴度；D1～D5为待定参数。该模型采用累积损伤来描述材料的失效过程，失效变量为：

式中：D 在0～1之间变化，初始值为0，当D=1时，材料失效；Δεep为一个时间步内的等效塑性应变增量；εf为当前时间步计算出的等效塑性断裂应变。

Bao-Wierzbicki失效模型也采用累积损伤准则，等效塑性断裂应变表达式如下：

式中：C1～C5为待定参数，分段函数在η=η0处连续。

在加载过程中，由于试件的变形，失效位置的应力三轴度在不断变化。一些学者针对缺口试件采用Bridgman 公式[12]计算应力三轴度，该公式计算值一般为初始状态下的应力三轴度。Bao等[7]则取变形过程中的平均值：

这种计算方式考虑了起裂前应力三轴度变化历程对断裂行为的影响，因此采用式（7）计算。

针对各个异形试件的拉伸或压缩过程开展有限元模拟分析，提取实际起裂位置的应力三轴度和等效塑性应变曲线，代入式（7）计算平均应力三轴度，下面展示部分计算结果。

图4是细长圆柱、光滑圆棒和45°缺口平板3种试件变形过程中的等效应力云图，图4(a)中试件在压缩载荷下中部出现墩粗，最大应力点位于圆柱中心。图4(b)中光滑圆棒在拉伸载荷下出现颈缩，最大应力点位于最小截面处。图4(c)中试件沿缺口尖端连线出现剪切破坏，最大应力点位于连线上。各试件体现出了预定的不同应力三轴度。

图4 试件等效应力云图Fig.4 Equivalent stressdistribution of specimens

图5和图6分别比较了细长圆柱和45°缺口平板试验载荷-位移曲线，数值模拟结果和试验均吻合较好，说明标定的Johnson-Cook 本构模型可以应用于不同应力状态的30CrMnSiNi2A 钢有限元模拟分析，据此能够提取较为准确的应力应变信息。

图7是试件失效位置应力三轴度随等效塑性应变变化的曲线，应力三轴度均从理论值（缺口圆棒采用Bridgman 公式，缺口平板依据平面应力分析获得）开始演化，光滑圆棒和缺口圆棒在拉伸过程中颈缩截面不断变小，应力三轴度越来越高；45°缺口平板在滑移过程中趋于纯剪切状态，应力三轴度有所下降；圆柱试件中部墩粗膨胀，压缩效应变弱，应力三轴度有所上升。总体而言在试件断裂之前应力三轴度变化范围不大，因此取平均是合理的，表4列出了各试件断裂处的平均应力三轴度和断裂应变。

图5 细长圆柱载荷-位移曲线Fig.5 Load-displacement curves of thin cylinders

图6 45°缺口平板载荷-位移曲线Fig.6 Load-displacement curvesof butterfly plates

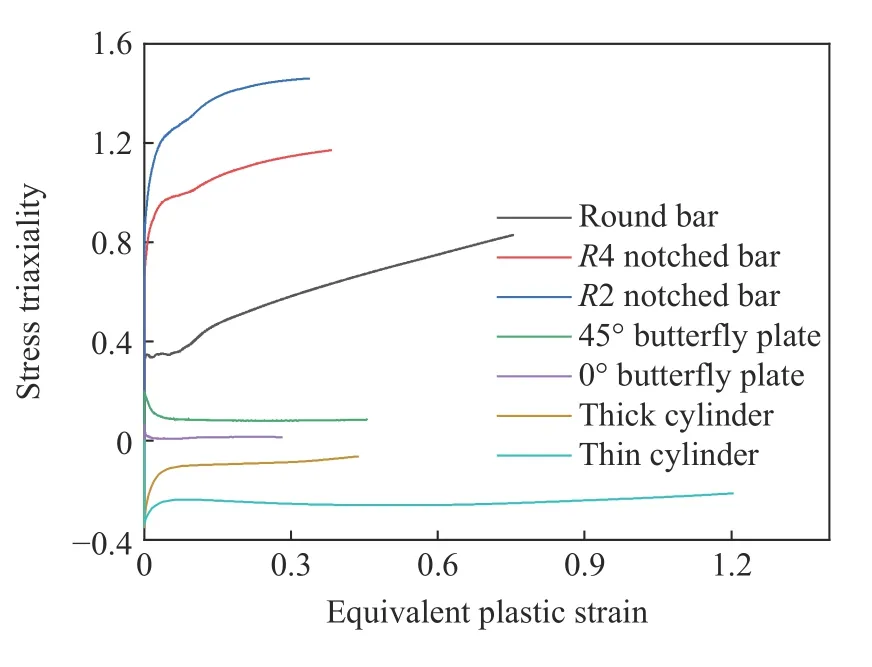
图7 各试件应力三轴度-等效塑性应变曲线Fig.7 Evolution of stress triaxiality for variousspecimens

表4 平均应力三轴度和断裂应变对应表Table 4 A summary of averagestress triaxiality and equivalent plastic fracture strain

Johnson-Cook 失效模型中D1～D3通过常温和准静态条件下的不同应力三轴度试验获得，为与文献[3]比较，本文只选取表4中高应力三轴度的5～7号数据进行参数拟合，得到D1=0.317，D2=5.504，D3=4.161。D4和D5通过不同温度和应变率条件下的光滑圆棒拉伸试验获得，根据表3中的断裂应变数据可以拟合得到D4=0.0218，D5=2.326。

综合拉伸、剪切和压缩试验的断裂应变和平均应力三轴度，可以得到较大应力三轴度变化范围内的30CrMnSiNi2A 钢韧性断裂特性。如图8所示，试验点的分布比较符合Bao-Wierzbicki失效模型的分段式函数，当应力三轴度低于-1/3时，断裂应变非常大，几乎不会破坏；当应力三轴度升高至0时，断裂应变不断减小，直至极小值；当应力三轴度从0开始增加时，断裂应变随应力三轴度增大而增大；出现极大值后，断裂应变随应力三轴度升高而减小。最后一段比较符合Johnson-Cook 失效模型，图8中给出了本文和文献[3]的拟合结果，两者比较接近，但是若外推到应力三轴度较小的区域时则与试验值均相差较大。经过拟合，Bao-Wierzbicki失效模型参数为：C1=0.248，C2=2.392，C3=0.317，C4=5.504，C5=−4.161，η0=0.424。

图8 断裂应变-应力三轴度曲线拟合Fig. 8 Fracture strain stress triaxiality curve fitting

Bao等[13]采用扫描电子显微镜观察了不同应力状态试件断口表面，发现2024-T351铝合金的损伤形式分为3种：负应力三轴度下损伤形式以剪切损伤为主，高应力三轴度下损伤形式以延性孔洞扩展损伤为主，之间则是两者综合作用。本文中3种试件的断口形态如图9所示，圆柱压缩破坏后表面产生斜裂纹，符合剪切损伤的特征；圆棒拉伸破坏后断口呈杯锥形，符合延性孔洞扩展损伤的特征，说明30CrMnSiNi2A 钢的韧性断裂行为比较接近上述损伤机理。

4 结 论

建立了一套测试高强度钢力学性能的方法，开展了一系列准静态、动态拉伸、剪切和压缩试验，结合有限元法模拟分析，研究了30CrMnSiNi2A 钢的韧性断裂特性，主要结论如下：

（1）研究了应变、应变率和温度对30CrMnSiNi2A 钢力学性能的影响，拟合出了相关的Johnson-Cook 本构模型和失效模型参数。30CrMnSiNi2A 钢在准静态到4 000 s−1应变率下屈服强度变化范围为1163～1 883 MPa，在室温到500°C温度下屈服强度变化范围为698～1 163 MPa，表现出一定的应变率敏感性和高温软化效应。

（2）设计了异形试件，试验获得了应力三轴度在（−1/3,1.5）之间的应力状态，构建了30CrMnSiNi2A钢断裂应变和应力三轴度之间的变化关系，确定了Bao-Wierzbicki 失效模型参数。

（3）30CrMnSiNi2A 钢在不同应力三轴度区间的断裂特性不同，应力三轴度高于0.424时，断裂应变随应力三轴度呈指数型衰减，比较符合Johnson-Cook 失效模型；应力三轴度在0附近时，断裂应变较小，与Johnson-Cook 失效模型预测值相差较大，而Bao-Wierzbicki 失效模型可以更好地描述低应力三轴度下30CrMnSiNi2A 钢的断裂特性。