一种新的三支扩展TAN贝叶斯分类器

张春英，冯晓泽，刘 洋，马逸涛，刘凤春，高瑞艳，任 静

1(华北理工大学 理学院，河北 唐山 063210) 2(华北理工大学 迁安学院，河北 唐山 063210) 3(河北省数据科学与应用重点实验室，河北 唐山 063210)

1 引 言

朴素贝叶斯分类器(Naive Bayes classifiers，NB)由Duda和Hart于1973年首次提出，因简单、高效而被广泛应用，但朴素贝叶斯分类器基于属性条件独立性假设，应用时此假设很难满足，故人们尝试对这一假设条件进行一定程度的放松，考虑部分属性间的相互依赖信息.文献[1]提出一种朴素贝叶斯分类器的树扩展—TAN贝叶斯分类器，它允许属性节点最多只依赖于一个非类节点.目前关于TAN贝叶斯分类器的研究主要是网络结构的构建，文献[2]提出了扩展的TAN贝叶斯分类器——SETAN贝叶斯分类器，考虑条件属性对类属性的贡献度差异，允许属性没有父节点，增强了分类准确性；文献[3]利用不确定属性间的依赖关系进行分类，提出了一种不确定正树扩展朴素贝叶斯算法；文献[4]提出了不考虑边重定向的TAN分类器学习算法，构建时以最大化LCL为优化目标；文献[5]采用条件对数似然方法增强了TAN贝叶斯分类器的类概率估计性能，提出了扩展的TAN贝叶斯分类器(ATAN)；虽然目前TAN的研究改进了分类模型，但这些分类模型均属于二支决策——接受或拒绝.实际应用中的数据存在不完整不确定性，简单的采取二支决策会对结果造成一定的损失.

三支决策[6，7]是Yao在粗糙集理论的研究过程中总结而来的一种理论方法，主要思想是将论域一分为三(正域、负域和边界域)，对每个论域都制定不同的决策策略，尤其是将延迟决策作为处理信息难以做出决策的决策方式，其符合人类的思想与认知.尽管三支决策在很多领域已取得很多成果，但条件概率的计算面临些问题[8].Yao 和 Zhou通过朴素贝叶斯模型估计条件概率，提出了一种朴素贝叶斯粗糙集模型，提高了计算效率[9]；文献[10]将三支决策与朴素贝叶斯分类器结合起来，并用于垃圾邮件的分类，除了把邮件分为正常邮件，垃圾邮件外，允许用户对于不确定的邮件进行进一步的检查，通过实验证明降低了误分类率.

为了缓解三支朴素贝叶斯分类器属性条件独立性假设的问题，本文融合TAN贝叶斯分类器与三支决策，提出一种新的三支扩展TAN贝叶斯分类器：3WD-TAN.在三支分类规则制定时，利用TAN贝叶斯公式估计三支决策中的条件概率P(Cc|xh)，构建了3WD-TAN贝叶斯分类模型，并通过对比实验验证了算法有效性.

本文其余部分的结构如下：第2节介绍了TAN贝叶斯分类器的相关工作；第3节融合TAN贝叶斯分类器与三支决策，提出一种新的三支扩展TAN贝叶斯分类器，并制定3WD-TAN贝叶斯分类规则，设计3WD-TAN贝叶斯分类器的分类流程，以及分析该分类器的时间复杂度从理论上验证可行性；第4节分析阈值(α,β)变化对分类结果的影响，并选取NB、TAN、SETAN算法进行对比实验，说明该分类器的可行性.

2 TAN贝叶斯分类器

树扩展朴素贝叶斯分类器(Tree Augmented Naive Bayesian Classification，TAN)由Friedman于1997年提出，是在朴素贝叶斯分类器的基础上弱化属性之间独立性要求而进行的扩展.TAN能有效利用属性间依赖信息，允许属性节点最多有两个父节点，其原理如下：

(1)

(2)

(3)

(4)

TAN贝叶斯分类器模型的详细构建过程如下：

1) 计算任意两个属性之间的条件互信息I(ai,aj|Cc)，i≠j，构建完全无向图；

(5)

2)构建最大权生成树；

根据不产生回路的原则，由上步无向图中边的权重大小选择边，直到选择n-1条边为止，构建出最大权生成树；

3)将无向图转换为有向图；

任意选择属性节点为根节点，以根节点为起始其它节点为结束设置边的方向，将无向图转换为有向图；

4)增加类节点及其指向各个属性节点的有向边，构建一个TAN模型.

3 3WD-TAN贝叶斯分类器

约定：给定信息系统S=(U,A∪D,{Va|a∈A},{Ia|a∈A})，其中，U为有限论域；A是属性集，表示为A={a1,a2,…,an}；D={C1,C2,…,Ck}表示k个不相交的决策类；Va是全部属性值的集合；Ia:U→Va是信息函数，将U属性a映射到Va，即Ia(x)∈Va.

本文通过融合TAN贝叶斯分类器与三支决策模型，提出了3WD-TAN贝叶斯分类器.本节将建立3WD-TAN贝叶斯分类规则，设计3WD-TAN贝叶斯分类器的分类流程，以及分析该分类器的时间复杂度从理论上验证可行性.

3.1 3WD-TAN贝叶斯分类规则

构建3WD-TAN贝叶斯分类模型的关键是条件概率的估计以及3WD-TAN贝叶斯分类规则的建立，因为条件概率P(Cc|xh)很难从可观察到的数值中估计，通常用贝叶斯公式进行变换.因此本文通过构建TAN贝叶斯分类器，利用TAN贝叶斯公式估计条件概率P(Cc|xh)，并考虑了属性间的部分依赖关系，使之能够取得较为精确的条件概率值.

(6)

将TAN贝叶斯公式(2)代入到式(6)中，由于在运算过程中，连加运算远比连乘运算计算量小，故加入后使得运算更简便[12].以最小风险理论为准则得到3WD-TAN贝叶斯分类规则：

(P)规则：如果：

则xh∈POS(α,β)(Cc)；

(N)规则：如果:

则xh∈NEG(α,β)(Cc)；

(B)规则：如果：

则xh∈BND(α,β)(Cc)；

(7)

其中：

(8)

3.2 3WD-TAN分类器设计及分析

3.2.1 分类器思想

为了解决传统二支决策TAN贝叶斯分类器在处理不确定性数据时具有较高的错分率，将三支决策思想与TAN贝叶斯分类器相融合，提出一种新的三支扩展TAN贝叶斯分类器：3WD-TAN.假设有训练集U={x1,x2,…,xN}和测试集T={t1,t2,…,tP}.首先，根据训练集U构建TAN贝叶斯分类器，利用式(5)计算任意两个属性的条件互信息I(ai,aj|Cc)，构建最大权生成树，将无向图转为有向图，增加类节点及指向各个属性节点的有向边，构建TAN模型；然后，考虑属性间的部分依赖关系，通过TAN贝叶斯公式估计三支决策中的条件概率P(Cc|xh)，并建立3WD-TAN贝叶斯分类规则；最后，利用3WD-TAN贝叶斯分类器对测试集T进行三支分类.具体的流程如下：

算法.3WD-TAN Bayesian classification

输入：训练集U={x1,x2,…,xN}，测试集T={t1,t2,…,tP}，每个类别的阈值(αCc,βCc)

输出：测试集T的分类结果{POS,NEG,BND}

1.构建TAN贝叶斯分类器

2.forai∈Ado

3.foraj∈Ado

4. 根据式(5)计算条件互信息I(ai,aj|Cc)

5.endfor

6.endfor

7.根据最大权生成树算法，构建最大权生成树

8.选择属性节点为根节点

9.forai∈Ado

10.以根节点为起始其它节点为结束设置边的方向，将无向图转换为有向图

11.endfor

12.增加类节点Cc

13.forai∈Ado

14.添加类节点指向各个属性节点的有向边

15.endfor

17.利用训练好的分类器对测试集T进行分类，对测试集T中的样本根据式(7)计算类Cc的正域、负域和边界域；

18.fort=1,2,…,pdo:

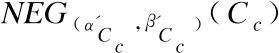
26.endif

27.endfor

28.return测试集T的三支分类结果{POS,NEG,BND}.

3.2.2 复杂度分析

从整体上考虑，本文提出的3WD-TAN贝叶斯分类器主要分为3个部分：

1)步骤1-步聚15主要是根据训练集U构建TAN贝叶斯分类器，此步主要耗时的是步骤2-步聚6中的计算任意两个属性之间的条件互信息I(ai,aj|Cc)和步骤7中的构建最大权生成树；

②步骤7中构建最大权生成树的时间复杂度为O(n2·logn)[13]；

一般情况下，N>logn，故在整个步骤1-步聚15构建TAN贝叶斯分类器的过程中，时间复杂度为O(N·n2)；

3)步骤17-步聚27对测试集T中的P个样本进行分类，时间复杂度为O(P).

综上，3WD-TAN贝叶斯器的时间复杂度为O(N·n2)+O(k)+O(P)=O(N·n2)+O(P).与TAN贝叶斯分类器相比，主要的区别在于步骤16-步聚17，故额外的时间复杂度为O(P)，因此本文提出的3WD-TAN分类器是可行的.

4 实验及结果分析

4.1 实验环境

为了说明3WD-TAN分类器的性能，实验选取UCI机器学习数据集中的5个不同规模的数据.数据集基本信息如表 1所示.该实验在基于Inter Core i7-6700的处理器，RAM为8.00GB的WIN7系统环境下的PyCharm 2018.3.4版本下实现.

表1 数据集基本信息Table 1 Dataset basic information

在实验的评价标准上，采取了Jia 和Shang提出的基于三支决策分类问题的评价标准[14]，如表 2所示.

表2 基于三支决策分类的混淆矩阵Table 2 Confusion matrix based on the three-way decision classification

其中n*·表示实际为类别·时判别为*的样本个数.

准确率(Accuracy)是对分类器在测试集上表现的总体评价，表示被正确划分的样本占被确定划分的样本的比例，如式(9)所示.

(9)

召回率(Recall)表示预测为正类占实际为正类的比例，实际为正类的样本不仅要考虑划分到正域、负域的正类样本，同时也要考虑划分到边界域的正类样本，如式(10)所示.

(10)

4.2 实验过程及结果分析

本文采用准确率(Accuracy)、召回率(Recall)分类指标进行性能评估，在实验中采用十折交叉验证的方法.对数据集的缺失值进行简单处理，对于条件属性，数值型用平均值代替，非数值型用众数代替；决策属性用众数代替.

4.2.1 阈值(α,β)变化分析

阈值(α,β)是3WD-TAN分类器的一个重要参数，通常介于0,1之间且α>β，(α,β)的选择会影响3WD-TAN的结果.为了分析不同的阈值(α,β)对结果的影响情况，本文在(0,1)之间以0.05为步长选取不同的(α,β)对UCI数据集进

图1 Vote准确率Fig.1 Vote accuracy

图2 Vote召回率Fig.2 Vote recall

图3 Car准确率Fig.3 Car accuracy

图4 Car召回率Fig.4 Car recall

行实验，并以Vote和Car数据集为代表分析阈值(α,β)变化对结果的影响.由于变化范围较小，为了更好的分析阈值变化对准确率和召回率的影响，将结果集中的部分展示(只展示了每个数据集的其中一种类别的部分结果情况)，如图1-图4所示.表3中列出了不同数据集在分类结果最优时所对应的阈值(α,β).

3WD-TAN分类器要求阈值(α,β)介于0,1之间且α>β.故在图1-图4中，当β≤α时，设置准确率和召回率的结果为0，主要讨论阈值α>β的情况并以Vote和Car数据集为代表分析阈值(α,β)变化对结果的影响.

图1与图2分别为Vote数据集在不同阈值(α,β)下的准确率和召回率的变化情况.由图1可知，3WD-TAN在数据集Vote下的准确率总体上在97.7%以上.当(αC1，βC1)在(0, 0.50)范围迭代变化时，准确率基本持平于97.7%；当αC1的迭代范围为(0.55, 0.90)，βC1的迭代范围为(0, 0.70)时，准确率增加到100%；当αC1的迭代范围为(0.95, 1)，βC1的迭代范围为(0, 0.70)时，准确率又降低到98.0%；当(αC1，βC1)在(0.75, 1)范围迭代变化时，准确率从97.7%逐渐降低到80.4%.由图2可知，3WD-TAN在数据集Vote下的召回率总体上在99.0%以上.当(αC1，βC1)在(0,0.55)范围迭代变化时，召回率基本持平于99.0%；当αC1的迭代范围为(0.60, 0.65)，βC1的迭代范围为(0, 0.65)时，召回率增加到100%；当αC1的迭代范围为(0.70, 1)，βC1的迭代范围为(0, 1)时，召回率从99.0%逐渐降低到89.3%.当阈值(αC1,βC1)=(0.65,0.40)，(αC2,βC2)=(0.60,0.45)时，准确率和召回率高达100%.故当阈值(α,β)的取值合适时，3WD-TAN的准确率和召回率优于NB、TAN和SETAN.

表3 不同数据集下每个类别的阈值Table 3 Thresholds for each class under different datasets

图3与图4分别为Car数据集在不同阈值(α,β)下的准确率和召回率的变化情况.由图3可知，3WD-TAN在数据集Car(C1类)下的准确率总体上在94.1%以上.当(αC1，βC1)在(0, 0.50)范围迭代变化时，准确率基本持平于94.1%；当αC1的迭代范围为(0.55, 0.80)，βC1的迭代范围为(0, 0.80)时，准确率增加到95.1%；当αC1的迭代范围为(0.85, 0.95)，βC1的迭代范围为(0, 0.95)时，准确率增加到98.0%.由图4可知，3WD-TAN在数据集Car(C1类)下的召回率总体上在99.0%以上.当(αC1，βC1)在(0, 0.55)范围迭代变化时，召回率基本持平于99.0%；当αC1的迭代范围为(0.60, 0.70)，βC1的迭代范围为(0, 0.70)时，召回率增加到100%；当αC1的迭代范围为(0.75, 0.85)，βC1的迭代范围为(0, 0.85)时，召回率又降低到99.0%；当αC1的迭代范围为(0.90, 1)，βC1的迭代范围为(0, 1)时，召回率从99.0%逐渐降低到81.1%.当阈值(αC1,βC1)=(0.85,0.60)、(αC2,βC2)=(0.80,0.50)、(αC3,βC3)=(0.75,0.55)和(αC4,βC4)=(0.65,0.40)时，3WD-TAN在数据集Car上的准确率为91.9%，略低于SETAN，但高于NB和TAN；召回率为97.0%，优于NB、TAN和SETAN.

综上，当阈值(α,β)取值合适时，3WD-TAN分类器的准确率和召回率在多数情况下优于NB、TAN和SETAN分类器.

4.2.2 对比实验

表 4给出了本文提出的3WD-TAN分类器与NB、TAN、SETAN分类器在5种数据集下关于表3所示的阈值参数下的准确率和召回率对比结果.

表4 准确率、召回率对比结果Table 4 Accuracy,recall comparison results

由表4得出，当阈值(α,β)取一定值时，绝大数情况下，本文给出的三支扩展TAN贝叶斯分类器(3WD-TAN)在二分类和多分类数据集上的结果高于SETAN分类器以及传统的NB、TAN分类器.且3WD-TAN贝叶斯分类模型适用于不同规模的数据集.

由二分类实验结果可知，3WD-TAN分类器在数据规模较大，属性较多的Mushroom数据集上的结果优于NB、TAN和SETAN分类器；对于数据规模较小，属性数目中等的Vote和Breast Cancer数据集，3WD-TAN分类器的准确率高于对比的分类器较多，故在处理数据规模小，属性数较多的数据集时，3WD-TAN依然效果良好.

由多分类实验结果可知，3WD-TAN分类器在数据规模中等，属性数目较小的Balance数据集上的结果优于NB、TAN和SETAN分类器；对于数据规模中等，属性数目中等的Car数据集，3WD-TAN分类器的准确率高于NB和TAN，略低于SETAN，但3WD-TAN分类器的召回率高于NB、TAN和SETAN.

从数据集的规模、属性数和类别数3个角度综合分析.相比较数据规模与类别数目，属性数量对分类结果的影响较大，但3WD-TAN贝叶斯分类模型的分类效果要优于NB、TAN和SETAN分类模型.

5 结束语

考虑到在分类过程中将不确定的对象强制划分到某个类中与人们的实际决策并不符合，文中将三支决策思想与TAN贝叶斯分类器相融合，提出了一种新的三支扩展TAN贝叶斯分类器(3WD-TAN)，将传统的TAN分类器推广为三支TAN分类模型.考虑属性间的部分依赖关系，通过构建TAN贝叶斯分类模型计算三支决策中的条件概率，改善了条件概率的计算，并一定程度上提高了TAN贝叶斯分类器的精确率.通过5个数据集的对比实验，验证3WD-TAN具有较高的准确率和召回率.然而，该方法是针对静态数据集进行分类的，下一步将考虑数据的动态特征，研究构建动态的3WD-TAN半朴素贝叶斯分类模型.同时TAN分类器的属性间依赖存在一定的限制，可考虑进一步研究3WD-贝叶斯网络模型.