一种变步长LMS自适应滤波的改进算法*
2021-03-21张海霞
吴 瑶,张海霞
(解放军91033部队,山东 青岛 266001)
0 引言
针对不同的应用场景,自适应滤波器可通过多次迭代的方法自动调节滤波器的各项参数,最终实现滤波器在不同的场景下均能实现较好的滤波效果[1]。自适应滤波器的关键在于自适应滤波算法的选择,在信号处理领域有以下几种常用的滤波算法:LMS自适应滤波算法、RLS自适应滤波算法、变换域自适应滤波算法、仿射投影算法、基于子带分解的自适应滤波算法等[2-8]。最小均方算法(Least Mean Square,LMS)具有较强的鲁棒性和简单易实现等诸多优点,在信号处理领域的系统辨识、噪声消除等场景中发挥了重要作用,成为一种常用的自适应滤波算法[3]。在部分对实时性要求较高的应用场景下,例如军事目标辨识、动态噪声消除等场景,高鲁棒性、高收敛速度是滤波的基本要求。显然,对于传统LMS算法来说,收敛速度与滤波精度之间难以调和的矛盾成为限制其在这些情况下应用的瓶颈之一。本文对传统LMS算法进行改进,引入调节函数改进模型,通过仿真信号处理实验进行验证,在大误差前提下,改进算法在保持传统算法精度的情况下,提高了算法的收敛速度,具有较强的实用价值。
1 LMS自适应滤波器基本原理
1.1 LMS自适应滤波算法
自适应滤波器基本算法流程示意图,如图1所示。
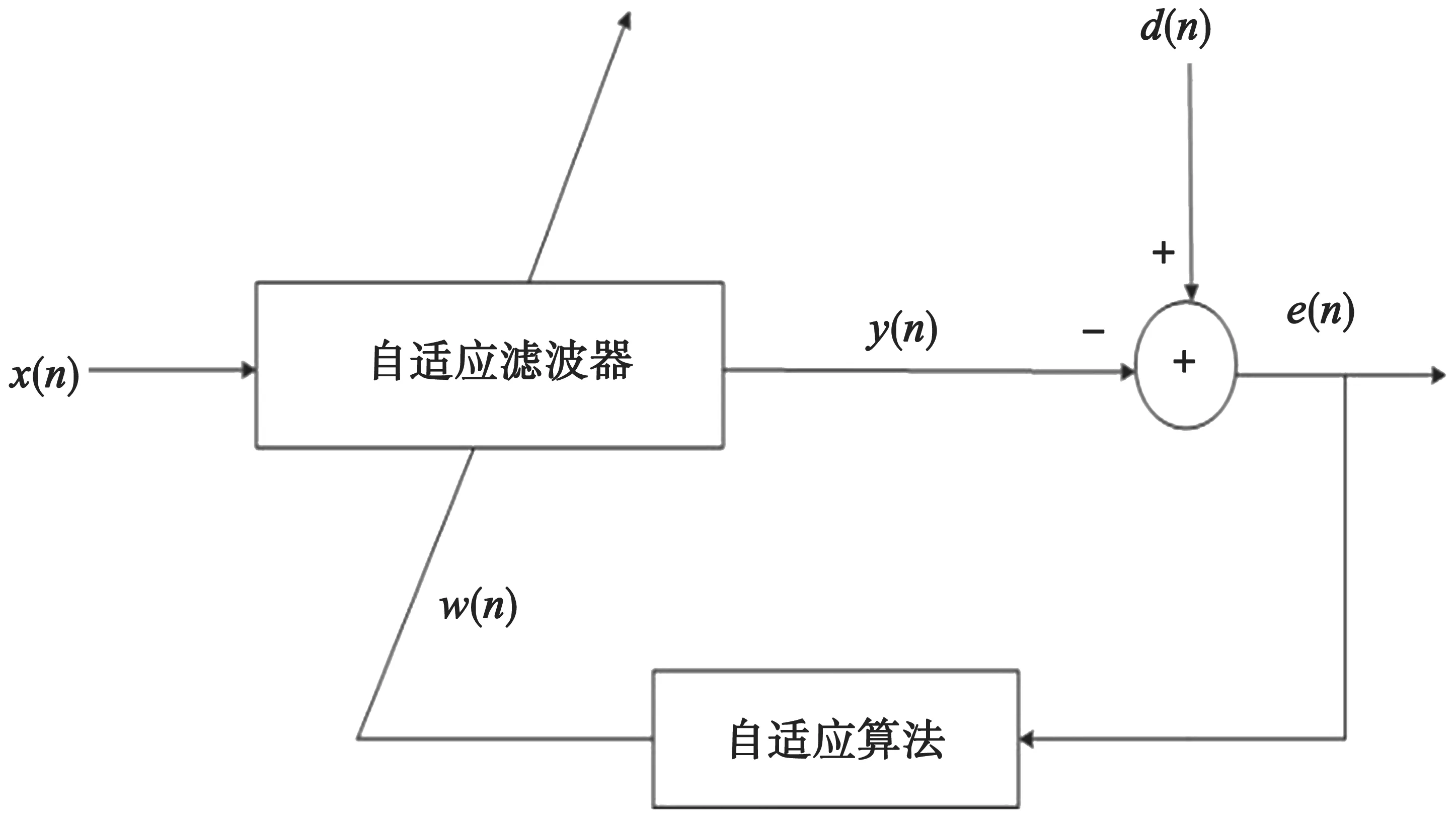
图1 自适应滤波器基本算法流程示意图
图1中,x(n)表示自适应滤波器在当前第n时刻的状态量输入;y(n)表示第n时刻状态量经过自适应滤波器估计后的结果输出;d(n)为第n时刻的期望响应;e(n)为滤波器的自动调节参数,主要含义为第n时刻的滤波器的估计误差;w(n)为n时刻自适应算法得出的滤波器加权系数。
LMS算法基本公式如下:
(1)经过滤波器估计后的输出结果:
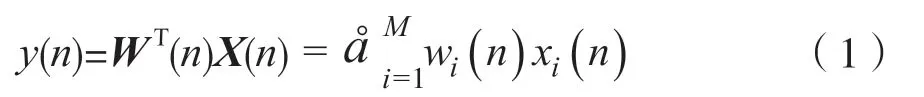
(2)估计误差:

(3)权系数更新:
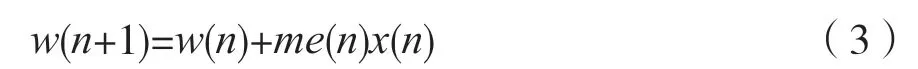
式中:X(n)为在n时刻滤波器的状态向量,即输入量,W(n)为自适应滤波器n时刻的权向量,M为自适应滤波器的迭代次数,μ为权系数更新的步长因子。其中:
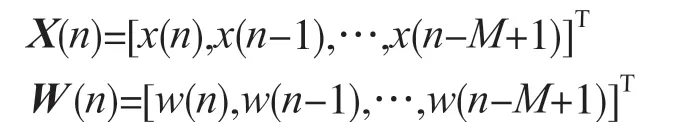
由文献[3]可知算法收敛的条件为步长因子μ满足:

式中:γmax为相关矩阵R{E[W(n)-W0]}的最大特征值,W0为维纳解。
1.2 变步长LMS自适应滤波算法
收敛速度和滤波精度共同构成评价滤波算法的性能指标。在要求算法收敛速度快的同时,还希望滤波精度高。对于滤波算法步长参数设置为固定值,当步长较小时,滤波精度较高,但收敛速度慢;当步长较大时,收敛速度较快,滤波精度较底。因此,采用固定步长的滤波算法在收敛速度、滤波精度方面难以做到两全其美。不可调和的矛盾已经成为了传统LMS应用的重要瓶颈,针对这些不足和局限性,也有学者提出了一些对于滤波算法的改进方法。
在众多对于传统LMS算法的改进方式中,例如变步长LMS算法、归一化LMS算法等[9-14],变步LMS算法以其简便可行的特点受到学者们的青睐。其中,比较具有代表性的是文献[15]中研究的通过Sigmoid函数对滤波的步长进行调节优化的算法[15],具体函数见公式(5):
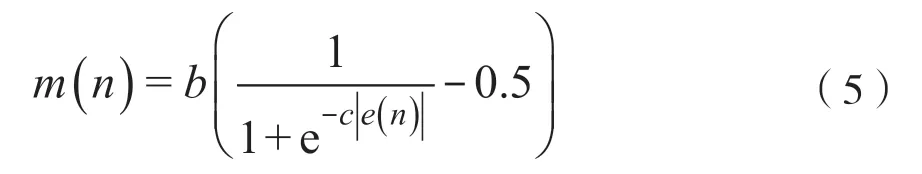
式中:Sigmoid函数的陡峭程度由参数c直接决定,与函数曲线上升的快慢成负相关;β表征Sigmoid函数中因变量的取值范围,决定了曲线的高度。由于在初始阶段,滤波估计结果误差值e(n)难以避免的存在较大的问题,与之对应的,在滤波中也应该取较大的步长值,这样就可以有效地保证滤波在初期就以较快的速度进行收敛;随着滤波的更新计算,算法逐步进入稳态,估计结果的精度随之提高,估计误差e(n)开始减小并趋于稳定,与之对应的,为确保滤波能够维持较小的稳态误差,具有较好的鲁棒性,在滤波中也应该取使步长值急剧减小。
张红梅等学者[3]对于变步长LMS滤波算法进行了深入研究,从基本原理着手优化数学公式算法,对文献[15]中变步长公式进行了改进,使其更加科学,加快了算法的收敛速度,在对实际水位信号的处理中取得了良好的效果。其变步长公式如下:
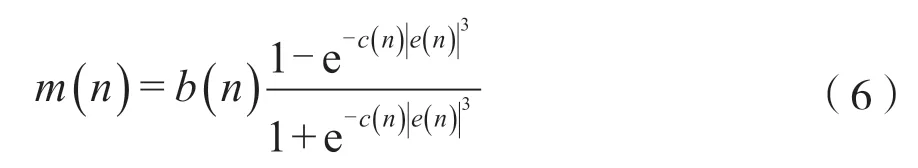
2 改进变步长LMS自适应滤波算法
2.1 调节函数
针对当前Sigmoid函数变步长最小均方算法的不足,在对其工作原理理论分析的基础上,对传统变步长LMS自适应滤波算法提出了一种改进方案。以Sigmoid函数为原型设计了一个调节函数,如式(7)所示:

式中:y为调节因子;a≥1。
当误差较小时,该函数值接近1,在此时调节函数基本不会影响变步长函数的性质;当误差较大时,该函数的函数值急剧增大,使得变步长函数的值变大,从而加快收敛。因此,该调节函数能在不改变原算法的稳态性质的同时,调节原算法收敛性质。
2.2 改进滤波函数
本文利用基于Sigmoid函数变步长最小均方算法函数(以下称为原函数)与调节函数相乘得到了一个改进的μ(n)与e(n)的非线性函数关系
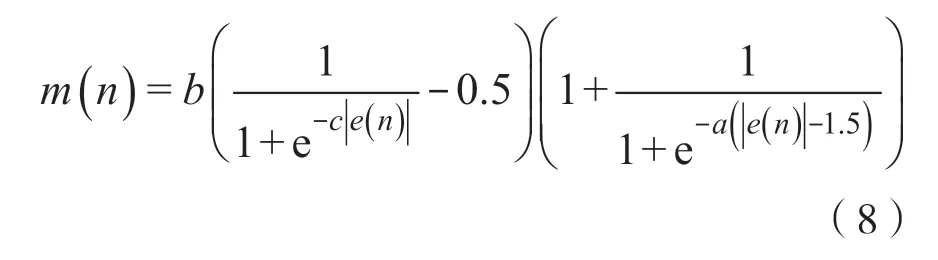

图2 调节函数曲线
其函数曲线如图3所示,由于μ(n)关于e(n)的步长改进函数是一个偶函数,因此以下主要论述e(n)≥0的情况。
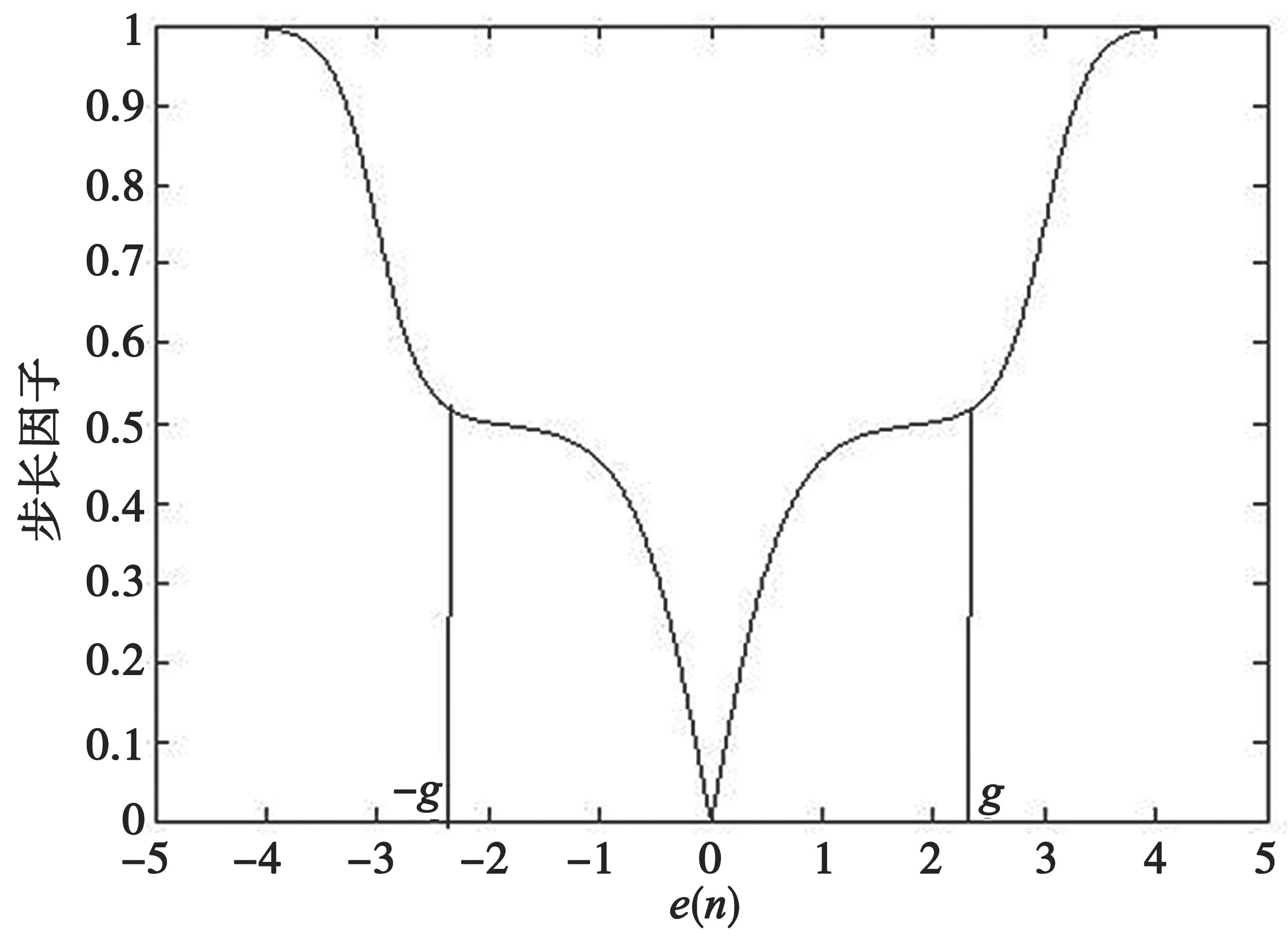
图3 改进函数曲线
观察图3的变化规律可知,函数曲线在一个阈值g两侧有不同的函数性质。当误差小于阈值g时,函数基本保持原函数的性质;当误差大于阈值g时,滤波的收敛速度成非线性类指数型增加,究其原因,主要是式(8)中对步长因子进行了膨胀增加调整,最终对于收敛速度的提高进行了优化。
下面具体讨论各参数对滤波特性的影响以及其确定方法。
图4为b=1、c=4、b=1.5时,步长因子与滤波估计误差在参数a分别取5、10、20时的关系曲线。

图4 参数a 取不同数值时改进函数曲线结果
由图4可知,随着a的增大,改进函数达到最大收敛值的速度不断加快,且误差的阈值也不断增大。在实际应用中,通常取a>5。
3 算法性能分析
仿真信号是幅值为4,频率为40 Hz,信噪比为-10 db的正弦信号,叠加噪声是均值为0的高斯白噪声。分别采用文献[3]、文献[15]和本文算法对其进行滤波处理得其收敛曲线如图5所示。
由图5可以看出,在滤波函数基本参数都相同的前提下,由于调节函数的作用,新算法在误差较大时的收敛速度较文献[3]与文献[15]明显加快;同时又在误差较小时能够保证较好的稳态性质,算法很好地兼顾了稳态性与收敛性,完全符合预期。
4 结语
为兼顾信号处理中稳态性与收敛性这一实际问题,本文对现有的变步长LMS自适应滤波算法进行了有效的改进。改进算法通过引入一个调节函数进行,使得新算法在保证原算法精度的情况下,较大程度上提高了算法在大误差下的收敛速度,进一步兼顾了算法的收敛性和稳态性。
