一种高精度变步长的大规模MIMO能效优化算法*
2021-03-21刘帅帅
刘帅帅
(杭州电子科技大学,浙江 杭州 310018)
0 引言
在过去的几十年里,通信技术得到快速的发展,通信用户和业务流量剧增的同时,通信技术产业能耗也急剧上升。能耗的上升,既增加了通信成本,又不符合绿色通信的要求,而大规模多输入多输出(Multiple-Input Multiple-Output,MIMO)技术作为如今通信系统最主要的技术之一,使用更多天线接收和转发信号,因此导致系统能耗上升,如何提高大规模MIMO系统的能效受到广泛关注[1-3]。
为了解决通信系统的能耗问题,通信小区的资源分配成为重要的研究方向。文献[4]通过合理的功率分配提高了通信系统的频谱效率和能量效率。文献[5]指出等功率分配方案无法充分利用能量,在考虑了基站天线数和小区内用户数影响的前提下,提出一种功率分配方案,仿真结果表明联合基站天线数、小区用户数的功率分配提高了系统频谱效率性能。此外,有学者通过优化基站天线数来提高大规模MIMO系统能效[6-8]。文献[6]推导了大规模MIMO上行链路在不同的接收方式的信道容量下界,并且通过合理分配基站天线数提高了系统的频谱效率和能量效率。文献[7-8]假设大规模MIMO基站天线数为一个常数,提出一种低复杂度的资源分配方案,通过优化发送功率提高了系统能效。文献[9]使用凸理论模型分析了天线数、用户数、发送功率等参数对大规模MIMO系统能效的影响,联合多参数优化系统能效更符合现实通信场景。因此文献[10-15]联合多参数对大规模MIMO系统的能效问题进行了研究,首先利用信道容量的闭合表达式建立能效函数,然后以能效最大化为目标对能效函数进行优化求解,得到最佳的资源分配方案。Mahdi等人[13]研究了一种低复杂度的大规模MIMO资源分配算法,将功率分配和天线选择进行了联合优化,利用交替迭代更新的方法求解最优能效,在不损失能效性能的前提下降低了算法复杂度。文献[14]考虑了大规模MIMO系统内每个用户的通信质量以及每根天线的发射功率是否合理的问题,以能量效率最大化为目标,对最优天线数以及功率分配方案进行了优化求解。
传统资源分配算法均采用固定迭代步长对最优能效进行优化求解[10-15],但合适的迭代步长不易确定,步长过大导致搜索精度不高,步长过小使算法复杂度上升。本文采用变步长的资源分配算法,根据算法循环迭代次数调整迭代步长,可变的迭代步长满足了算法搜索精度,另外配合一种快速收敛算法加快算法收敛,降低算法的复杂度。本文在第1节介绍了大规模MIMO上行链路系统模型和能耗数学模型;第2节建立能效目标函数并提出本文算法,然后对算法复杂度进行了统计分析;第3节进行了仿真和分析。数值实验结果表明,本文算法具有精度高、收敛快等优势,可有效应用于大规模MIMO系统下的复杂的多用户场景。
1 系统模型
本文假设一个单小区多用户大规模MIMO上行链路系统,基站配置M根发射天线位于小区中央,小区内有K个单天线移动用户随机散布在基站四周,且满足M>>K,小区模型如图1所示:

图1 MIMO系统模型
在大规模MIMO上行链路系统中,信道矩阵H受大尺度衰落和小尺度衰落的影响。根据参考文献[6],信道矩阵生成表达式为:

式中,D表示K×K维的大尺度衰落对角矩阵,对角线上的元素[D]kk=βk。βk表示用户k到基站天线的大尺度衰落系数,其中包括几何衰落和阴影衰落的影响。由于基站天线之间的距离远小于用户到基站的距离,因此用户k到达基站任何一根天线的大尺度衰落系数均视为βk。G表示M×K维的小尺度衰落矩阵,服从CN(0,IM)的瑞利分布,该模型可有效应用于小尺度衰落建模中。
若所有用户在同一时频资源中传输数据,基站端收到M×1维信号y为:

式中,P表示用户K×K维发射功率对角矩阵;对角线上的元素[P]kk=pk,pk表示用户k的发送功率;x是K×1维发射信号向量;n是M×1维的加性高斯白噪声。
文献[6]假设基站端可以获得完美信道状态信息(Channel State Information,CSI)且噪声方差为1,采用最大比合并(Maximal Ratio Combining,MRC)接收,得用户k的信道容量Rk为:


上行链路的大规模MIMO系统的能耗模型主要分为移动端的能量消耗和基站端的能量消耗两部分。第一部分移动端能量消耗被建模为所有单天线用户发射总功耗,第二部分基站端的能量消耗表示为调用M根天线所消耗的总功耗。基于上述考虑,通信系统的总功耗Ptot可建模为:

其中,为了方便表示小区内所有用户的发射功率,本文将发射功率矩阵P对角线上的元素取出,重组为1×K维的用户发射功率向量p=[p1…pK],pe为基站端每根天线的射频链路上所有电子器件产生的平均功率。
大规模MIMO系统能效被定义为单位能量所传输的数据量[6],为了使系统能效最大,联合用户发送功率p和基站天线数M进行资源分配,将p和M作为自变量,根据式(4)和式(5),得到上行链路能效函数F(p,M)为:

2 变步长梯度下降算法
2.1 能效目标函数
实际通信系统中考虑到每个用户的通信质量,定义用户的最低通信质量为ξ。令每个用户的上行传输速率不低于最低通信质量,得到另外,考虑到多用户MIMO系统内用户间干扰对能效性能的影响,定义用户间干扰上限J=2.0[15],利用干扰上限J对整个系统发射功率约束,得到综合上述考虑,对能效函数式(6)建立约束条件得:
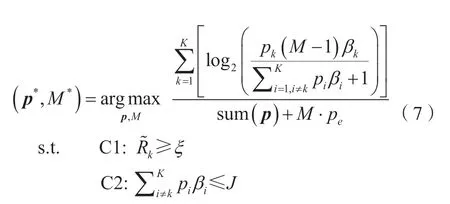
式中,(p*,M*)表示使能效最大的发送功率和天线数。文献[15]假设用户间干扰最大为J,此时为通信可能的最坏情况,则上行链路总传输速率大于最坏情况下的传输速率,即:
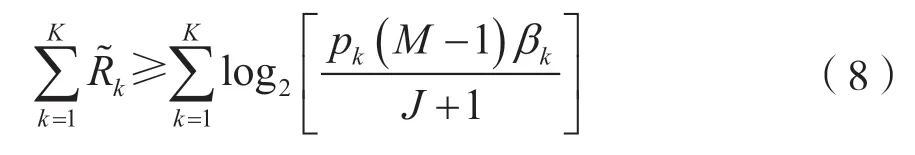
系统能效函数为F(p,M),为了考虑可能存在的通信的最坏情况,基于式(8)最坏情况下传输速率的闭合式,将能效函数转化为:


为了研究目标函数L关于p、M的凹凸性,利用文献[17]附录A中证明目标函数凹凸性的方法求得式(10)的海森矩阵:

由于目标函数L的定义域domL={pk,M|pk>0,M∈N+}为一个凸集,且在该定义域内海森矩阵为负定矩阵,因此目标函数L关于p、M是联合凹的[11,20]。
2.2 变步长梯度下降算法
传统的资源分配算法通常采用牛顿法对最优解进行迭代更新,在迭代过程中采用固定迭代的步长,且步长决定迭代的次数,也决定着算法搜索的精度。如果采用大步长,则可以减少迭代次数,但搜索精度不高;若为了提高精度而采用小步长,则会增加算法的复杂度。变步长(Variable Step Size,VSS)算法是一种自适应调整步长的算法,其原理是利用迭代次数自动更新步长。在迭代过程的前期采用大步长以满足迭代速度,在迭代过程的后期采用小步长以满足搜索精度。但随着迭代过程的不断进行,VSS算法的小步长同样会大幅提升算法的复杂度。文献[18]在Dinklebach算法基础上提出了一种快速收敛的Dinklebach(Fast Convergent Dinklebach,FCD)算法,可以显著提高收敛速度。本文提出的算法结合了VSS算法和FCD算法的优点,相比于传统算法,本文算法在用户数较多的大规模MIMO系统中更高效,具体实现步骤如下。
变步长梯度下降算法


VSS算法在步骤4和步骤5中将迭代次数用于拉格朗日乘子更新。随着迭代进行,拉格朗日乘子更新步长越来越小,收敛精度也随之提高。FCD算法在步骤7中得到一个含次梯度的中间阈值a,将中间阈值计算过程退化为邻域牛顿法,其至少是一个超线性收敛[18],提高了算法收敛速度。因此,本文算法兼备了VSS算法和FCD算法精度高和收敛快的优点,性能更好。
2.3 复杂度分析
为了分析本文算法的运算复杂度情况,采用文献[19]统计浮点数的方法对算法每个步骤进行了复杂度统计,得到如表1所示的结果。

表1 本文算法各步骤运算复杂度
从表1可以看出,各步骤的运算复杂度与小区内用户数K有关,用户数越多,算法运算量越大。此外,能效最优解的求解需要多次迭代,每迭代一次,步骤2~步骤8运算一次,因此算法的运算复杂度和迭代次数n有关。基于上述讨论,表2给出了各算法运算复杂度统计结果,其中ni(i=1,2,3,4,5)表示不同算法的循环迭代次数。

表2 各算法运算复杂度
从表2可以看出,各算法的运算复杂度分为两个部分,第一部分是初始化运算量,为了对比各算法的性能差异,各算法进行相同的初始化运算,因此初始化浮点运算量相同;第二部分是各算法对能效最优解迭代进行求解所对应的运算量,与迭代次数和小区内用户数有正相关关系。
3 仿真结果及分析
本文假设小区内用户随机分布在基站四周,由文献[15]可知,可按用户到小区基站的距离将所有用户均分为三类,大尺度衰落系数分别为[1 0.8 0.5]。对算法进行初始化运算,天线数M0=10,初始化发射功率p0=[0.1 … 0.1]TW,使用于对比的各算法运算起点相同。本文的对比算法有RABM+VSS算法、RABM+FCD算法、RABM算法[15]和JUAPA算法[21],其中RABM+VSS算法和RABM+FCD算法是为了探究VSS算法和FCD算法会对RABM算法的性能产生怎样的影响。仿真所需的主要参数在表3中给出。

表3 仿真参数
图2给出了不同用户数情况下各算法的能效性能差异,从图中可以看出各算法能效性能由高到低为:RABM+VSS算法、本文算法、RABM算法[15]、RABM+FCD算法、JUAPA算法[21]。RABM+VSS算法在拉格朗日乘子递推公式中,步长自动更新,随着迭代的进行,步长越来越小,对最优解的搜索精度不断提高,因此能效性能比RABM算法更好。RABM+FCD算法是一个超线性收敛的迭代过程,求解判决阈值的效率更高,加快迭代过程的结束,但是会降低一定的计算精度,因此能效性能比RABM算法略有降低。本文算法在VSS算法基础上,将FCD算法用到VSS算法中,提高了VSS算法的收敛速度,但损失了部分能效性能,因此本文算法能效性能较VSS算法略低,但本文算法保留了VSS算法能效性能的高增益。在用户数K=40时,本文算法能效达到3.85 bit/Hz/Jourl,比RABM算法提高了30%左右,随着用户数增加该比例还在不断变大。RABM算法相比于JUAPA算法考虑了用户间干扰情况,随着用户数不断增多,用户间干扰更不容忽视,这种用户间的干扰严重影响系统能效性能,因此JUAPA算法的性能相对较差。
图3给出了不同用户数下各算法的最优天线数。可以看出,随着小区内用户数的不断增多,基站最优接收天线数基本呈线性增加。在小区内用户数较少的情况下,各算法对应的最优天线数基本相同,这是因为在用户数较少的通信场景下,资源分配的过程简单且用户的相互影响小,各算法都能优化出最优的能效性能。
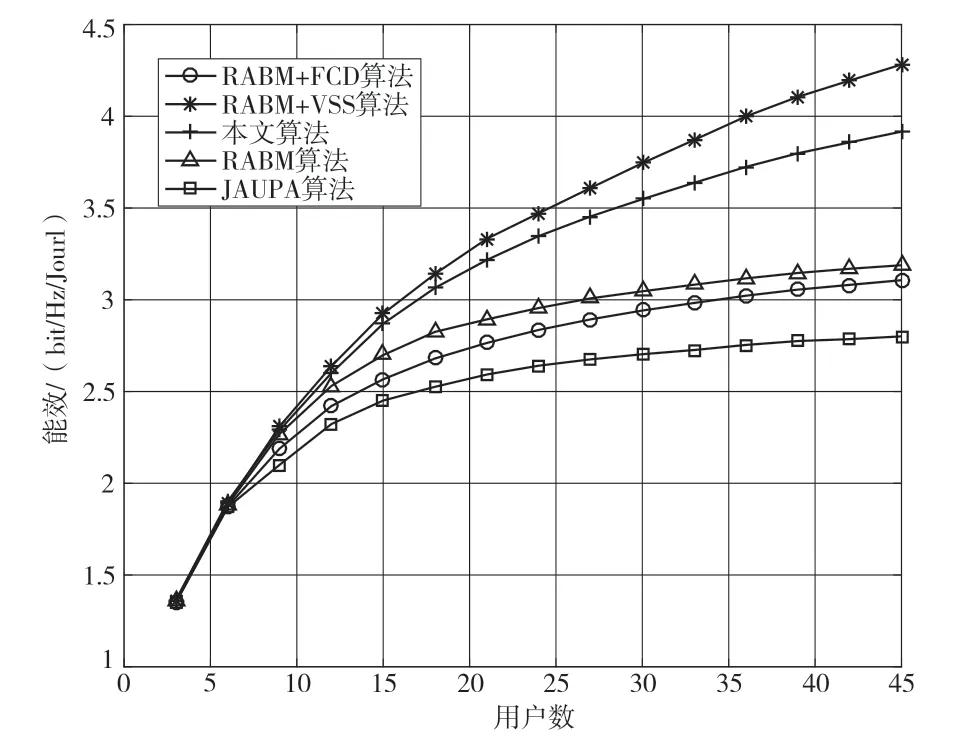
图2 不同用户数时各算法的能效性能

图3 不同用户数时各算法的最优天线数
图4给出了上行链路的发射功率随用户数不同的变化情况,从图中可以看出,随着小区内用户数增加,发射功率先增大,然后趋于稳定。这是因为在小区内用户数较多的通信场景下,基站调用更多的天线更有利于提高系统能效。

图4 不同用户数情况下各算法最优发送功率
图5给出不同用户数情况下天线总功耗的变化情况。通过图5可以看出,随着小区内用户数的增多,为了提高系统总上行速率,基站使用更多天线进行接收,因此天线总功耗持续上升。通过对比图5的基站端天线总功率和图4的用户发射总功率,基站天线带来的能量损耗成为总能耗的主导因素,在大规模MIMO系统的资源分配中,天线数的优化至关重要。
图6给出各算法在不同用户数情况下求解最优能效所需的循环迭代次数。RABM+VSS算法采用变步长迭代,迭代次数越多对应的搜索步长越小,因此导致RABM+VSS算法要比RABM算法迭代次数多,尤其在小区内用户数较多,资源分配较复杂的情况下,循环迭代次数巨幅增加。
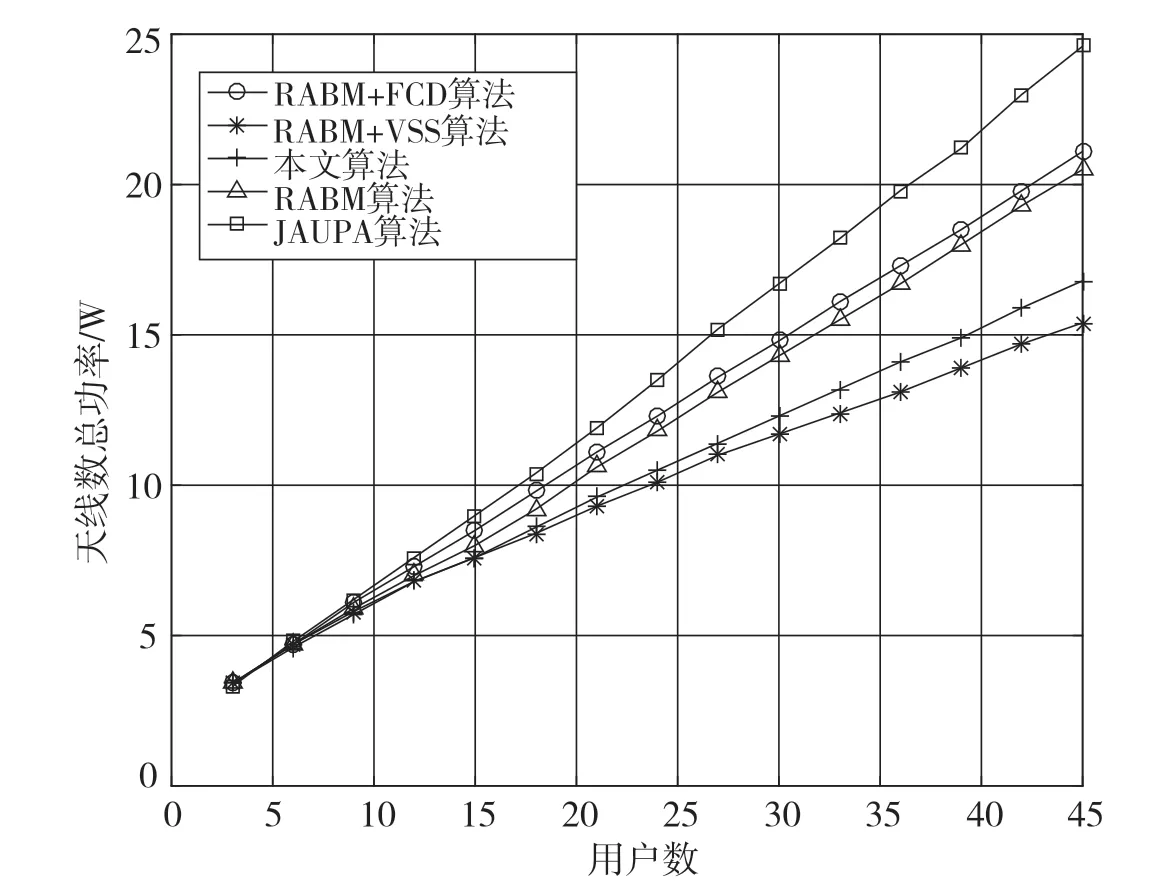
图5 不同用户数情况下各算法天线总功率

图6 不同用户数时各算法的迭代运行次数
相反,RABM+FCD算法的超线性收敛则加快了RABM算法的收敛速度,因此迭代次数要少于RABM算法。本文算法利用FCD算法收敛快的优点,显著降低了VSS算法变步长带来的复杂度,循环迭代次数较VSS算法大大降低,仅比RABM算法略高,在可接受范围内。JAUPA算法忽略用户间干扰对系统能效的影响,简化了能效模型,目标函数更容易趋向收敛,因此迭代次数最少。
图7给出了不同用户数时各算法的浮点运算量。2.3节的算法复杂度分析结果显示,各算法的浮点运算量跟循环迭代次数n和用户数K有关,从图6看出随用户数K增加,循环迭代次数n也增加,因此各算法的浮点运算量增长速度比图6的循环迭代次数增长速度快。

图7 不同用户数时各算法浮点运算量
4 结语
在使用MRC接收机的大规模MIMO上行链路系统中,本文提出一种精度高、收敛快的资源分配算法。所提算法利用分式规划性质把能效函数转化为减式形式,再用拉格朗日乘子法把约束条件合并到目标函数,最后把VSS算法和FCD算法结合起来求解能效最优解。VSS算法可以提高算法的搜索精度,FCD算法可以加快算法的收敛速度,因此本算法在兼顾了算法复杂度的同时提高了搜索精度。仿真结果证实,在大规模MIMO系统中用户数较多(K>40)的情况下,本文算法可将系统能效提高30%左右,这是因为在用户数较多的情况下,基站天线功耗在总功耗中占主导地位,而本文算法经过精确地迭代搜索找到更准确的天线数,降低了基站调用天线数量,由此提高了系统的能效,有较理想的工程实际应用意义。
