一种融合常数模与深度学习的水声信道均衡算法*

刘振兴，陆剑锋，李 平

(1.泰州职业技术学院，江苏 泰州 225300;2.南京信息工程大学，江苏 南京 210044)

0 引言

通信质量的好坏取决于所处信道的物理特性。由于水声信道具有时变、空变、多途、高背景噪声等复杂特性，其不可避免地将在通信系统的接收端产生严重的码间干扰，从而引起误码，降低了系统的可靠性[1-3]。因此，如何克服传输信道引起的时变多途效应一直是研究者们关注的焦点。

目前，常用的方法有常数模算法（Constant Modulus Algorithm，CMA）[4]、小波[5]和多小波[6-7]等多种水声信道均衡算法。常数模算法不需要知道水声信道的先验信息，因结构简单、性能稳健、运算量小而被广泛使用，但其收敛精度不高。小波和多小波算法的均衡效果与其变换的稀疏能力有关，且需事先选取小波和多小波系数，影响了算法的实际应用。

深度学习技术在通信、图像处理、计算机视觉等领域的成功应用为解决这一问题提供了一个新的方向[8-11]。该技术不需要获取信道模型的先验信息，可以通过端到端的训练直接从训练数据中学习有效的网络模型，处理任何类型的信道。文献[12]对基于深度学习的正交频分复用水声通信系统进行了研究，将深度前馈神经网络作为通信接收机，用训练后的网络模型直接恢复发射信号。文献[13]对基于深度学习的时变水声信道单载波通信进行了研究，将深度前馈神经网络作为接收器，利用训练后的网络模型恢复发射信号。以上方法采用深度前馈神经网络作为均衡器将接收端信号直接恢复为发射信号，但当通信环境差、干扰严重时，系统接收端输入信号与理想输入信号相差较大，描述接收信号与发射信号之间关系的函数也更加复杂，网络训练的难度将变大，训练后的模型精度也会受到严重影响，从而使信号的误码率增加，影响通信质量。

基于此，本文提出了一种结合常数模与深度学习的水声信道均衡算法。该算法设计了用于信道均衡的CMA-SAE系统接收端结构。该结构在通信系统接收端，首先采用CMA对输入信号进行均衡处理，实现对发射信号的快速均衡，然后采用SAE对均衡后的信号进行去噪处理，实现对发射信号的高精度恢复。此外，该算法提出了一种新的堆栈自编码网络训练方法，实现了对网络的逐层训练，进一步提高了网络的性能。

1 相关工作

1.1 常数模均衡算法

CMA是一种经典的盲均衡算法，由于其算法简单、性能稳健、运算量小，且不需要周期性地发送训练序列，有效地提高了信道利用率，因此被广泛使用。

均衡器输出为：

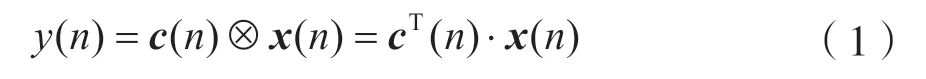
式中，x(n)为均衡器输入信号，c(n)为均衡器权系数向量，⊗表示共轭卷积。

损失函数定义为：

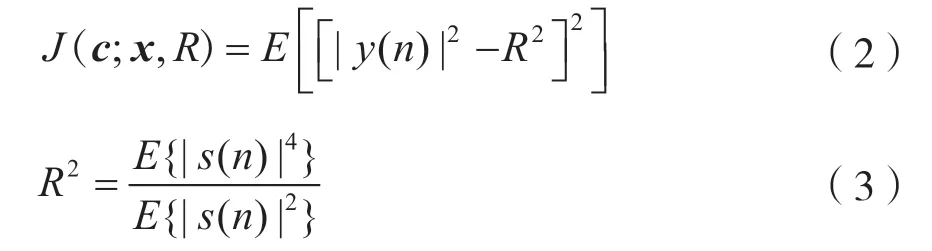
式中，R2为CMA模值，s(n)为零均值独立同分布的发射信号，E{}表示期望。

采用随机梯度法更新权系数：

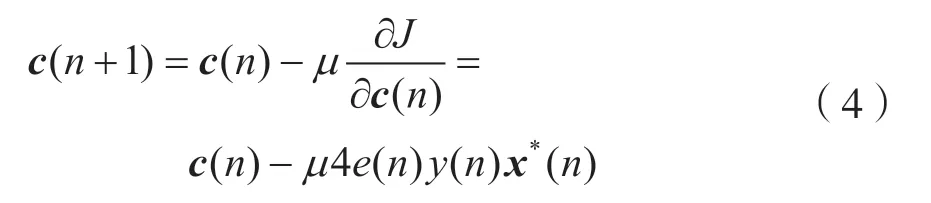
式中，c(n+1)为下一次迭代的均衡器权值，c(n)为当前迭代的均衡器权值向量，e(n)为误差，x*(n)为均衡器输入信号x(n)的共轭，μ为所述均衡器的学习速率。

1.2 堆栈自编码器

自编码器是自监督神经网络，其输入等于输出。当输入为含噪信号，输出为干净信号时，学习的自编码器具有较好的去噪性能，故其常用于去噪。研究表明，网络的性能与其结构有关，深度网络相较于浅层网络，在稳定性和表达能力上更具优势，且堆栈自编码器可以模拟人的大脑活动，逐层提取低噪数据特征，重构无噪数据，故具有更好的去噪能力[14-15]。堆栈自编码器网络模型如图1所示。

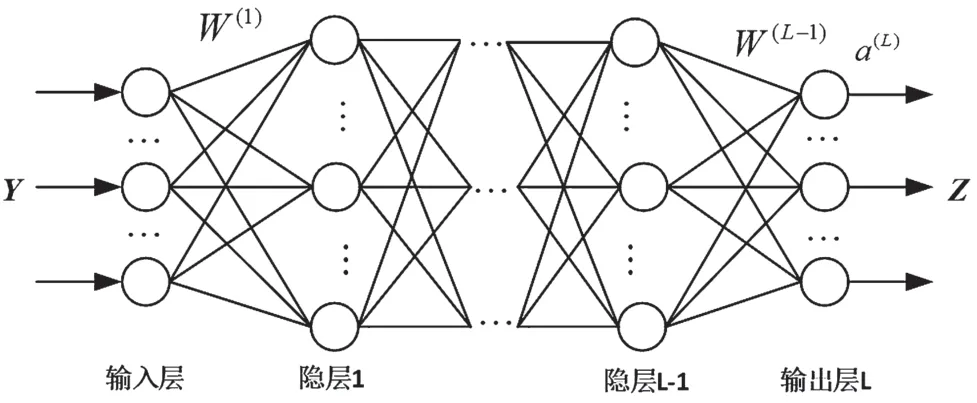
图1 堆栈自编码网络

网络计算公式如下:

式中，Y∈Rn表示输入的含噪声信号，p(L)表示第L层的输入，a(L)表示第L层输出，a(1)=p(1)=Y，W(L)表示网络第L+1层和L层之间的连接权值，b(L)表示与L+1层节点相连接的偏置，f(·)表示激活函数。

损失函数定义为：

Pascal Vincent[16]等对基于去噪自编码器的深层网络构建策略进行了研究，将网络训练分为预训练和微调两个阶段，采用“贪婪法”逐层训练整个深度网络。实验结果表明，随着隐层层数的增加，网络的性能不断优化，并且预训练后的网络性能优于无预训练的网络。该方法在网络逐层训练的过程中，采用人为添加噪声的方式构建训练样本集，但由于环境等因素的不确定性，噪声情况极为复杂，往往是未知的，故该方法存在一定的缺陷。

2 基于CMA-SAE的水声信道均衡算法

2.1 算法原理

本文提出的基于CMA-SAE的水声信道均衡算法原理如图2所示。其中，s(n)为零均值独立同分布的发射信号，h(n)为水声信道，v(n)为加性高斯白噪声，d(n)为理想的系统接收端输入信号，x(n)为实际的系统接收端均衡器输入信号，s^(n)是系统接收端输出信号。

图2 基于CMA-SAE的水声信道均衡算法原理框图

基于CMA-SAE算法的通信系统接收端主要包含CMA均衡和SAE去噪处理两部分，充分利用了CMA快速均衡和SAE高效去噪功能，从而实现发射信号的高精度恢复。此外，针对水声通信中常见的高阶QAM信号，添加了实复变换模块，进一步提升了模型的泛化能力。

2.2 算法描述

2.2.1 CMA均衡

CMA在所提出的算法中起均衡作用，完成对输入信号的初始恢复。根据算法原理，类似于聚类，主要步骤流程如下：

（a）根据式（1）计算均衡器输出；

（b）根据式（2）、式（3）计算损失函数；

（c）根据式（4）更新均衡器权系数；

（d）返回步骤（a），依次循环。

2.2.2 实复变换

当信道传输高阶QAM信号时，考虑到SAE网络特性，为了降低信号处理的复杂度，需要在SAE的输入端做信号变换，将复数信号变换为实数信号。为了使信号不失真，在SAE的输出端需做信号反变换，将实数信号变换为复数信号。变换原理如图3所示。

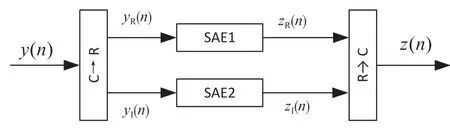
图3 信号变换原理框图

图中，y(n)=yR(n)+jyI(n)为SAE输入的复数信号。对y(n)进行信号变换转换为两路实数信号yR(n)和yI(n)，分别送到SAE进行处理。zR(n)和zI(n)为与之对应的两路堆栈去噪自编码器输出信号，经过信号反变换后转换为复数信号z(n)，z(n)=zR(n)+jzI(n)。

2.2.3 堆栈自编码器去噪

Pascal Vincent[16]等提出的逐层训练堆栈自编码器的“贪婪法”，由于无法获知噪声的先验信息存在一定的缺陷。本文提出了新的堆栈自编码器训练法，采用含噪信号和标签逐层训练堆栈自编码器。该方法与Pascal Vincent等的“贪婪法”的不同之处在于，含噪信号为通信系统接收端的输入信号，而不是人为给标签添加噪声获得的信号。另外，训练下一层网络时提取的是噪声信号和标签的特征作为训练数据集，而不是标签的特征作为网络的输入。具体过程如下：

（a）构建训练数据集。

（b）预训练网络。

①将原堆栈自编码网络的输入层、隐层1构成第一个去噪自编码网络。根据式（5）～式（8）计算网络输出及损失函数，采用批量梯度下降法对网络进行训练，得到网络参数W(1,1)、W(1,2)、b(1,1)和b(1,2)，其中W(1,1)和b(1,1)为网络的编码阶段参数，W(1,2)和b(1,2)为网络解码阶段的参数，令W(1)=W(1,1)，b(1)=b(1,1)。

②将原堆栈自编码网络的隐层1作为输入层，隐层2作为隐含层，构成第二个去噪自编码网络。利用W(1)和b(1)得到输入Y和的一阶特征表示h(1)和，将h(1)和分别作为第二个去噪自编码网络的输入和期望输出，训练网络，得到参数W(2,1)、W(2,2)、b(2,1) 和b(2,2)，令W(2)=W(2,1)，b(2)=b(2,1)。其中：

f(·)选择tanh函数，即f(t)=(et-e-t)/(et+e-t)。

③依此类推，直至训练完整个网络。在训练当前层自编码器时，其他层自编码网络参数保持不变。

（c）微调整个网络。

3 实验结果及分析

为了验证所提出算法的有效性，采用MATLAB 2015b进行了仿真实验，与文献[12-13]所提出的基于深度前馈神经网络的均衡算法DNN进行了对比。实验中，发射信号为16QAM，信号长度为12 000，采用混合相位信道h=[0.313 2,-0.104 0,0.890 8,0.313 4][17]，CMA权长16，深度前馈神经网络结构DNN为128-1024-612-128-32，堆栈自编码器网络结构SAE为128-200-300-400-128。除特别说明外，所有参数都如上所示。

3.1 算法性能分析

为了分析CMA-SAE算法的性能，采用CMASAE对输入信号进行了均衡。系统各部分输出信号星座图如图4所示。

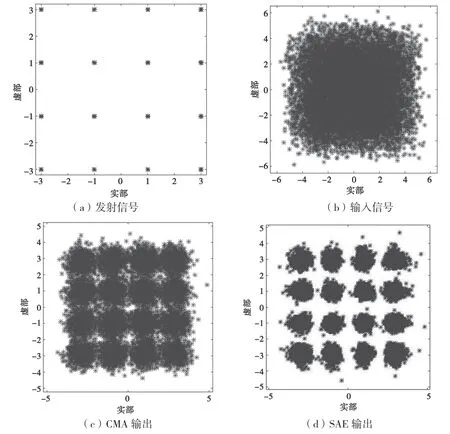
图4 星座图

由图4可知，所提出的CMA-SAE算法中，CMA对发射信号进行了初始估计，SAE对发射信号进行了精确恢复。由图4（c）可知，因为CMA模值为常数，它的主要作用是将信号向以模值为半径的圆聚拢，而实际参考信号为16个元素构成的方阵，故CMA处理后的信号具有较大的均衡误差，输出星座图分布较松散，但与系统输入信号相比，星点有序地分布在发射信号附近。由图4（d）可知，在CMA-SAE算法中，SAE对CMA输出的信号进行了进一步的估计，有效去除了CMA输出信号中的噪声，对发射信号进行了精确恢复，输出的信号星座图相对于CMA更紧凑，与发射信号更为接近。

3.2 SAE结构对CMA-SAE性能的影响

文献[16]指出，网络的性能会随着网络层数的增加而提升。为此，分析了网络节点数对网络性能的影响，对比了5层网络不同节点数下CMA-SAE输出的星座图，如图5所示。

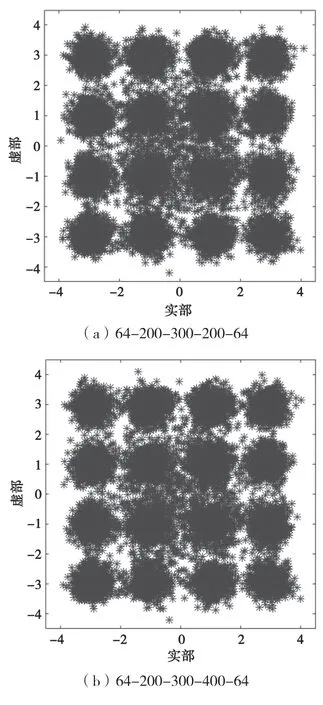
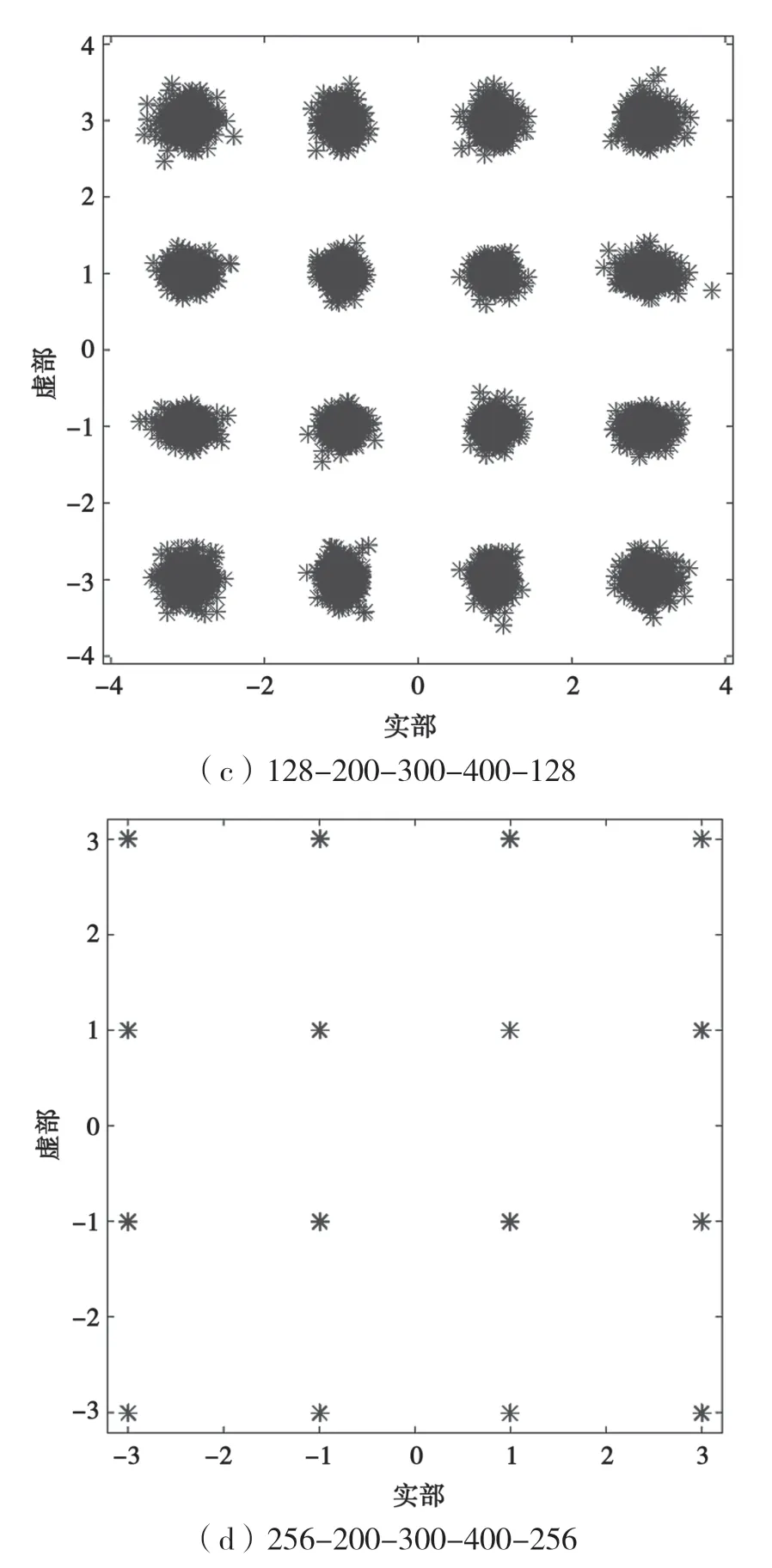
图5 不同网络结构的输出星座图

由图5（a）和图5（b）可知，采用网络结构64-200-200-200-64和64-200-300-200-64时，输出信号较紧凑地分布在发射信号附近，能实现信号的较精确恢复，但在中心点(0,0)附近，有较多散点，且两种结构输出的星座图相差不大。由图5（c）可知，采用网络结构128-200-300-400-128时，输出信号的星座图更紧凑，且中心点(0,0)附近的散点问题也得到解决，能更精确地恢复发射信号。由图5（d）可知，采用网络结构256-200-300-400-256时，输出信号非常完美地恢复出了发射信号。故由图5可知，网络的性能会随着网络输入层节点数的增加而提升。同时，由实验可知，当网络输入层节点数增加到一定数量时，网络性能达到最优，继续增加时网络的性能会急剧下降，输出的星座图完全发散。因为网络输入层节点数越多，意味着获取的信息越丰富，越有利于网络做出判断，但在数据总量不变的情况下，当输入层节点数逐渐增加时，意味着训练样本数的逐渐减少，当样本数过少时，不利于网络进行学习训练，从而性能会急剧下降。此外，对不同网络层数的自编码网络也进行了实验。由实验可知，随着网络层数的增加，网络性能逐步提升，但当进一步提升网络层数，即L＞5时，网络性能提升不明显，图中未列出。

3.3 算法比较

将本文提出的CMA-SAE算法与基于深度前馈神经网络的均衡算法DNN和基于堆栈自编码网络的均衡算法SAE进行了比较，比较了不同迭代次数k下，不同输入信噪比时算法的误码率。

图6 不同迭代次数的误码率曲线

图6（a）和图6（b）分别为迭代次数k=1 000和k=400时3种算法处理后的误码率。由图可知，CMA-SAE的误码率最低，SAE的误码率低于DNN，并且随着输入信噪比的增大，3种算法的误码率逐渐降低。因为SAE与DNN相比，包含一个逐层训练的预训练过程，故在相同的反向传播训练次数情况下，SAE的性能优于DNN。CMA-SAE与SAE相比，由于经过CMA预处理，CMA-SAE中SAE的输入信号与参考信号的差异较小，故两者的SAE经过相同的训练次数后，CMA-SAE相较于SAE表现更优。3种算法完成的是一个逆滤波过程，实现通信系统接收端输入信号与发射信号的逆向映射，可表示为函数f-1。通信环境越差，干扰越严重，接收端实际输入信号与理想输入信号相差越大，函数f-1越复杂，网络训练的难度也越大，训练后的模型精度也越差，故随着输入信号信噪比的减小，误码率逐渐升高。

对比图6（a）和图6（b）可知，随着网络训练次数的增加，算法的性能显著增加。当输入信噪比为5 dB时，CMA-SAE的误码率由训练次数k=400时的0.251 7提升到了k=1 000时的0.008 7。可知网络的训练次数对算法的性能具有重要影响，且训练次数越多，所提出的CMA-SAE与DNN和SAE相比，性能越优。

4 结语

本文提出了一种结合常数模与深度学习的新的水声信道均衡算法。该算法将现有水声信道均衡技术中的均衡、去噪功能分割开来，分别采用CMA和SAE进行处理。利用CMA估计发射信号，实现快速均衡；利用SAE去除CMA的估计误差，实现发射信号的精准恢复。水声信道仿真结果表明，提出的CMA-SAE算法优于最新的基于深度前馈神经网络的均衡算法DNN和基于堆栈自编码网络的均衡算法SAE，具有更低的误码率。此外，实验表明，算法的性能与深度神经网络的结构有关，会随着网络输入层节点数的增加而提升，也会随着网络层数的增加而提升，但当增加到一定数量时会出现饱和，继续增加时算法性能会快速衰退。算法的性能也与网络训练的次数有关，会随着训练次数的增加而提升，但训练次数的增加会带来计算量的显著增大。