融通算理与算法，构建运算模型

2021-03-21刘必雄

数学教学通讯·小学版 2021年11期

刘必雄

[摘要] 培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。以“两位数乘两位数”的教学为例，提出了在计算教学中融通算理与算法，建构运算模型的基本策略，提升学生运算能力，发展学生的数学素养。

[关键词] 算理;算法;运算;模型;小学数学

借助实物原型、直观模型等，引导学生在探究中明确算理，并在此基础上提炼出算法，最后将这种算法推而广之，建构起数学运算模型，是运算教学行之有效的方法。笔者以“两位数乘两位数”的教学为例，论述了在计算教学中融通算理与算法，建构运算模型的基本策略，期望对广大教育同仁有所借鉴和思考。

一、创设情境，引出新问题

“教学的艺术并不只在于传授本领，更在于激励、唤醒和鼓舞学生。”在运算教学中，教师可结合学生的实际生活创设生动情境，把学生置于一定的情境之中，引发学生的思维冲突，激发学生参与课堂的兴趣。

师：学校举行队列表演，一共有12行，每行有14人，有多少人参加队列表演呢？

生1：应该用乘法计算。列式为14×12。

师：同学们能试着计算它的结果吗？

（学生讨论。）

生2：我先算10行，每行14人，这样一共是10×14=140（人）;再算剩下的2行，一共是2×14=28（人），因此一共有140+28=168（人）。

生3：我把每行14人看成是（10+4）人，12行就是有12个10和12个4，所以有12×10=120（人），12×4=48（人），这样一共就有120+48=168（人）。

师：同学们真聪明。但是，在计算两位数乘两位数的时候，总是这样列三个式子，显得太麻烦了。

生4：是呀，我们还需要探索一种竖式计算方法，这样就能快速计算得数了。

教学中，教师结合学生的生活创设教学情境，把枯燥的数学计算融入解决现实生活问题的情境，这样既为学生提供了探索数学知识的现实资源，又使学生切身体验到了计算与现实生活的密切联系，使学生在解决问题中产生认知冲突，为下一步的探究学习奠定基调。

二、数形结合，充分理解算理

算理是算法的内在依据，理解算理可以让学生在增长知识的同时获得智慧。数学家华罗庚曾言：“数缺形时少直观，形缺数时难入微。”数形结合既是一种重要的数学思想方法，还是一种常用的教学方法。在教学中，教师可不失时机地为学生提供生动的图形材料，使抽象的数量关系变得具体起来，促进学生的数学理解，以起到事半功倍的教学效果。

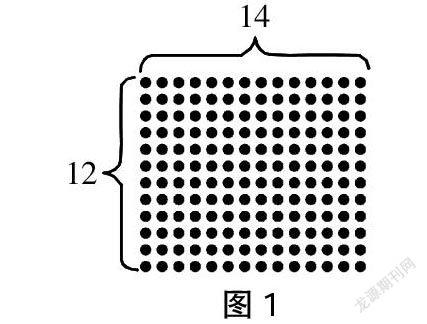
师：我们在学习“两位数乘一位数”时，采用了点子图帮助我们理解笔算的原理。现在，我们还用点子图帮助我们理清数量关系。（教师出示点子图，如图1所示）

师：请同学们以小组为单位，利用点子图，圈一圈，画一画，列式算一算。

（学生探究，教师巡回指导。）

生5：我把前6行圈起来，再把后6行圈起来，这样就把点子图分成了相等的2份，列式为14×6=84，84×2=168。（如图2）

生6：我把点子图的前10行圈起来，再把剩下的2行圈起来，列式为14×10=140，14×2=28，140+28=168。（如图3）

生7：我是这样圈的，把点子图分成4个部分，分别列式为10×10=100，10×4=40，10×2=20，2×4=8;然后把它们加起来，即100+40+20+8=168。（如图4）

师：你们都是借用点子图来理解和分析问题，并用自己的方法求出了14×12的积。那么，请同学们观察一下，这些方法有什么共同点呢？

生8：都是把其中的一个两位数拆成了两部分进行计算。

师：为什么要拆分？

生9：我们没有学过两位数乘两位数的笔算方法，把其中的一个两位数拆分成整十数或一位数，这样就转化为我们已经学过的知识了。

师：对。转化是一种重要的数学思想。通过把未知知识转化为已知知识，就能够促进问题的解决。请同学们再想一想，你认为哪种转化的方法比较好呢？

生10：我认为把12分成10和2这种方法比较好，因为无论是14×10=140还是14×2=28，计算起来都比较方便一些。

教学中，教师引导学生充分借用点子图的直观形象性用各种方法计算出了14×12的积，在圈一圈、算一算的过程中，学生不但理解了数形结合的精妙，而且还初步体验了把未知知识转化为已知知识的重要性;教师逐步引导学生“取好择优”，从多种解决问题的策略中找到最优化的方案，从而在下一步把算理与算法沟通，为突出竖式算法模型打下基础;教师采取数形结合的策略引导学生理解两位数乘两位数的算理依据，为学生的思维搭建一座联系算理与算法的桥梁，使学生从本质上找到算理的“根”。

三、提炼算法，建构运算模型

算理与算法是计算教学中相互融合的整体。学生在理解算理后，并不能马上形成算法，这就要求教师要抓住时机，顺势而教，在算理和算法之间铺路搭桥，让学生在体验交流的过程中充分理解算理，沟通直观与抽象、具体与概括之间的关系，从而促进学生提炼算法，建构运算模型，形成运算技能。

师：现在，同学们能够尝试用竖式计算14×12吗？请同学们以小组为单位进行合作交流。

（学生探索，教师指导。）

师（整理好学生竖式计算的过程，并归类）：同学们，这是大家列出的4种竖式，你能说一说哪种对，哪种错吗？（如图5）

生11：第①种不对，把12看作10，乘积是140，怎么会只有42呢？

生12：第①种算法中，14×2=28，14×10=140，所以“4”應该写在十位上，与上面的“2”对齐，“1”应该写在百位上。

生13：第②种竖式的结果是对的，但是从中看不出计算步骤。

生14：第③种笔算方法的结果也是对的。但是，我觉得用十位上的“1”乘14，在百位上写“1”，在十位上写“4”，就能够表示140了，末尾的“0”可以删去，这样就更加简便了。

生15：第④种笔算方法是正确的，而且还非常简洁。

师：你能具体说一说第④种笔算方法的过程吗？

生15：第一步，用个位上的“2”乘14，即2×4=8，把“8”写在个位上;再有2×1=2，把“2”写在十位上。第二步，用十位上的“1”乘14，即1×4=4，把“4”写在十位上;1×1=1，把“1”写在百位上。最后，把两次得到的积加起来，一共是168。