基于OptiStruct的万向联轴叉头孔两侧圆弧结构优化

胡斌， 谭邦俊，张宝霞，王艳，何贵生， 彭超

1.滁州职业技术学院 机械与汽车工程学院，安徽 滁州 239000；2.锐志微创医疗科技(常州)有限公司，江苏 常州 231000；3.松下家电(中国)有限公司，浙江 杭州 310000

0 引言

与齿轮传动、带传动和链传动等传动机构相比，联轴器有独特的优势,应用领域比较广泛[1]。万向联轴器中法兰叉头与焊接叉头在装配后存在一定间隙，而叉头是联轴器中最重要的部件之一。当万向联轴器叉头孔两侧圆弧出现最大应力时，叉头容易断裂。可以利用万向联轴器叉头装配间隙优化叉头，降低叉头的最大应力，提高叉头使用寿命[2-4]。

本文以SWC-225CH型万向联轴器为研究对象，采用有限元软件HyperMesh对叉头进行力学分析，评价其可靠性。以降低叉头装配区域应力为目标，采用OptiStruct优化叉头装配间隙区域。

1 叉头的力学分析

万向联轴器叉头装配简图如图1所示(图中单位为mm)。

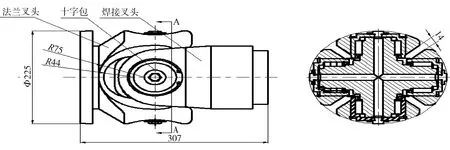
a)正视图 b)A-A剖面图图1 万向联轴器叉头装配简图

1.1 前处理

采用有限元软件HyperMesh对叉头进行力学分析前，需对叉头进行前处理[5-9]。

1)网格划分。对叉头进行几何清理，清理一些对分析结果影响不大又可以简化网格的工艺部分[7]。叉头共划分为154 472个节点，753 988个单元。

2)材料。法兰叉头的材料为35CrMo，弹性模量为2.06 TPa，泊松比为0.3，密度为7.8×103kg/m3。

3)约束。根据万向联轴器实际工作情况，叉头底部固定不动或者在HyperMesh软件中约束叉头底部6个自由度[10-11]。

4)加载。万向联轴器叉头受力情况复杂，叉头不同部位应力状态不同[12]。在不同方向上，有的单纯受拉，有的单纯受压，有的两拉一压，有的三向全压，需要寻找不同强度理论下的危险部位，再将屈服强度(疲劳强度)除以安全系数，计算比较笼统[13]。SWC-225CH型万向联轴器最大工况扭矩Mmax=40 kN·m，叉头两孔中心距L=28 mm，则每个孔承受载荷Fmax=Mmax/L=147 kN。在有限元软件中采用经典保守加载方式[14]，叉头与十字轴通过滚针连接传动，根据滚针轴承的受力特点，叉头受力位置在叉孔中心B点两侧且呈75°角对称分布，前处理后得到有限元模型如图2所示。

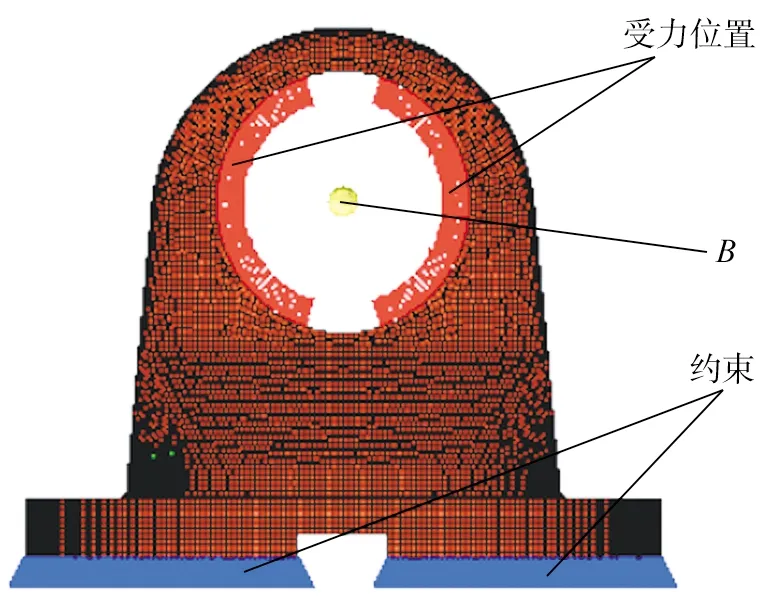
图2 有限元求解模型

1.2 分析结果

由HyperMesh后处理器查看分析结果之前，在叉孔两侧圆弧位置用2D网格进行耦合处理，考虑叉头两侧圆弧区域复杂且不易观察[15-16]，用2D网格求解得叉头两侧圆弧的应力云图和位移云图，如图3、4所示(图3单位为mm，图4单位为MPa)。

图3 叉孔两侧圆弧位移云图 图4 叉孔两侧圆弧应力云图

由图3、4可知，静力学分析状态下叉头两侧圆弧的最大位移为0.294 4 mm,最大应力为244.9 MPa，而极限应力为334 MPa，对叉头进行优化设计，降低最大应力，从而提高叉头强度。

2 叉头拓扑优化

2.1 优化设计三要素

OptiStruct优化属性模型可表述为:

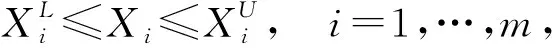
式中：X=(x1,x2,…，xn)为设计变量，如产品的结构、尺寸等参数；f(X)为目标函数，如各种力学性能或者质量；g(X)和h(X)为需要进行约束设计的响应函数，如对产品工作时的变形和应力水平进行约束。其中设计变量、目标函数和约束条件被称为设计三要素[17]。

在软件OptiStruct中对叉头结构优化三要素进行设置。

1)建立目标函数。以降低叉头孔两侧圆弧区域(见图2)的最大应力为优化目标，建立目标函数。

2)选择设计变量。选择叉头孔两侧圆弧区域上所有的网格和节点为设计变量。

3)设定约束条件。在软件OptiStruct中对叉头进行拓扑优化时，优化区域容易出现无限迭代情况，而根据图1可知两叉头在装配中有一定间隙，拓扑优化无限迭代容易出现结构上的干涉现象。在两叉头中间部分设置7 mm边界网格层，保证叉头优化结构工艺时不出现干涉，优化结果如图5所示(红色为边界网格层，蓝色为优化区域)。

图5 优化边界层

根据三要素定义，可得到

Minimize 0≤σmax≤244.9 MPa，

Subjectto 0≤R1≤75 mm，

0≤R2≤44 mm，

0≤T≤7 mm，

式中：σmax为叉头两侧圆弧最大应力，R1为叉头两侧圆弧区域最大外圈圆角，R2为叉头两侧圆弧区域最大内圈圆角，T为叉头装配间隙。

2.2 优化结果

采用优化后处理软件进行求解，得到目标函数曲线图、应力云图和优化后的形状变化云图，如图6～8所示(图7单位为MPa，图8单位为mm)。

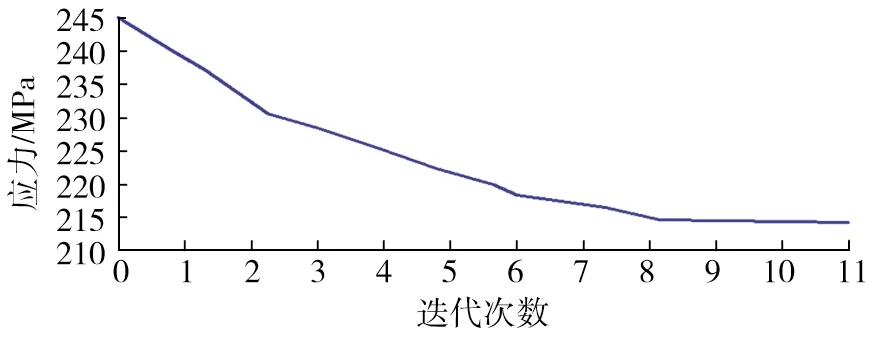
图6 目标函数曲线图

由图6可知，经过11次迭代优化运算之后，叉头孔两侧圆弧区域的应力由244.9 MPa下降到213.2 MPa。由图7可以看出利用万向联轴器叉头结构装配间隙可降低该区域的应力。虽然最大变形增加了6.39 mm，但未超过万向联轴器叉头装配间隙7.00 mm。

图7 叉孔两侧圆弧优化后应力云图 图8 形状优化云图

3 叉头结构改进

3.1 改进方案

由图8可看出，最大变形增加了6.39 mm，其他地方变化很小或者几乎无变化。叉头孔两侧圆弧区域应力降低31.6 MPa，但叉头形状的变化不利于加工生产。因此，叉头孔两侧圆弧区域优化过程中，避免法兰叉头、十字包和焊接叉头干涉，结合联轴器工程实际运用[18-19]，将装配间隙增加了6.40 mm，如图9所示(图中单位为mm)。图9a)结构改进前孔两侧圆弧为R75 mm和R44 mm，图9b)改进后孔两侧圆弧为R81.4 mm和R50.6 mm。

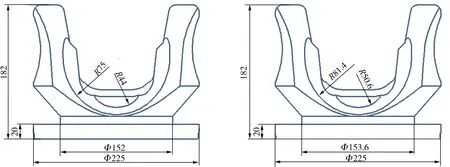
a)改进前 b)改进后图9 结构改进前后对比

3.2 力学分析

改进叉头结构后，重新建立叉头的三维模型和有限元模型，按照有限元计算步骤重新定义材料、工况和约束。最后求解得叉头孔两侧圆弧结构改进后叉孔两侧圆弧的应力云图和位移云图如图10、11所示(图10单位为MPa，图11单位为mm)。

图10 结构改进后叉孔两侧圆弧应力云图 图11 结构改进后叉孔两侧圆弧位移云图

由图10可知，叉头结构改进后，叉头孔两侧圆弧的最大应力为222.5 MPa，虽然大于拓扑优化时的213.2 MPa，但是小于原有叉头结构的最大应力244.5 MPa。叉头改进后的最大位移为0.247 mm，比原有结构减小0.05 mm。

4 结论

为解决万向联轴叉头孔两侧圆弧处出现最大应力，导致叉头断裂的问题，采用有限元HyperMesh软件对叉头进行力学分析，通过软件OptiStruct优化叉头结构。

1)对叉头进行有限元计算，得到叉头孔两侧圆弧处最大应力为244.9 MPa，需要优化叉头结构，提高叉头强度。

2)对叉头孔两侧圆弧进行拓扑优化，叉头孔最大应力由244.9 MPa下降到213.2 MPa，应力下降12.9%，改善了叉头结构性能。

3)通过拓扑优化降低了叉头的最大应力，但其结构不易加工，以拓扑优化中形状变化6.39 mm为理论数值，对叉头孔两侧圆弧进行结构改进。改进后重新进行有限元计算，得到最大应力为222.5 MPa，最大位移为0.247 mm，不仅提高叉头结构强度，也满足叉头的加工制造要求。