面向光伏消纳的“大机小网”系统两阶段优化调度

莫若慧，余加喜，贾 浩，范亚洲，余 洋

（1.海南电网电力调度控制中心，海南 海口 570203；2.华北电力大学 河北省分布式储能与微网重点实验室，河 北 保 定 071003）

0 引言

海南电网负荷用电规模较小，其发电机组数目有限，且机组单机容量较大，属于典型的“大机小网”结构。根据规划，未来海南电网光伏出力将达到15%以上[1]，由于光伏出力的随机性和波动性，“大机小网”结构下的海南电网将面临更加严重的功率不平衡问题[2]。

为应对光伏接入后“大机小网”的功率不平衡问题，海南电网陆续投入数座海蓄机组，形成了火电、光伏和海蓄机组的联合运行系统。针对类似联合运行系统的调度方法，文献[3]提出一种火电-风电-海蓄联合调度方案，利用抽水蓄能作为风电的优先备用，以平衡风电预测不确定性误差。文献[4]将可中断负荷与可转移负荷作为可调度出力，进行了火电-光伏-海蓄-需求响应联合安全经济调度研究，结果表明需求侧负荷可提高系统运行经济性。文献[5]，[6]采用多级调度方案，以弃风最小为目标建立模型，分析了日前优化调度与滚动优化模型间的关系。多级调度是在多个时间尺度下完成调度方案的协调优化，可统一考虑日前、日内甚至更小时间尺度下的调度优化组合[7]。针对多级优化调度问题，文献[8]，[9]进一步利用模 型 预 测 控 制（Model Predictive Control，MPC）进行滚动优化，将火电与风电的有功出力作为状态量，建立了火-风机组的多级滚动优化调度模型，该方法相比单时段优化更具优越性。文献[10]基于 随 机SMPC（Stochastic MPC，SMPC）提 出 了 考 虑负荷响应的电网联合调度方法，在风电不确定性较大时，需求响应能为系统运行带来更大的灵活性，降低系统运行成本。

多级调度可根据更高频率的光伏功率预测结果来实现更准确的优化调度[11]，不过当前多级调度研究大多针对间歇式电源接入的互联大电网，鲜见讨论“大机小网”下火电-光伏-海蓄-需求响应多系统联合运行的优化调度问题。为此，本文在考虑需求响应和海蓄机组运行特点的基础上，提出了规模化光伏接入“大机小网”的两阶段优化调度方法，该方法通过在日前调度中引入光伏未消纳量损失成本，提高了光伏消纳量；考虑负荷需求响应，建立考虑分时电价的时序负荷模型与需求响应成本模型，实现“削峰填谷”和多目标经济运行；同时，由于光伏出力预测存在误差，将SMPC作为日内滚动优化的基本框架，引入海蓄机组来平衡预测误差，实现电力系统优化调度的经济性。经过海南电网实际算例验证表明，本文提出的调度方法是有效的。

1 研究框架

1.1 需求响应模型

本文主要考虑分时电价响应机制：当负荷水平较高而光照不足时，将制定相对较高的电价，以引导用户避开该用电时段，有效降低负荷尖峰；反之，通过制定有吸引力的电价，鼓励用户将其它时段的用电需求转移至该时段，有效提高光伏消纳量。通过分时电价需求侧响应机制，“大机小网”系统可靠性低的问题将得到一定程度地改善。本文引入分时电价需求响应模型[12]：

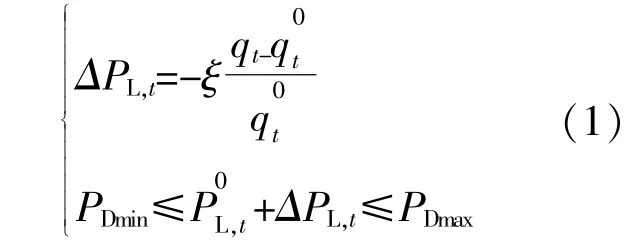
式中：ΔPL，t为引入需求响应后的负荷变化量；为系统需求响应前的负荷值；-ξ为分时电价需求响应系数；qt为t时段的电价；Dmax，Dmin分别为用电量最大值和最小值。

在分时电价需求响应机制中，电价峰谷差会影响用户响应程度，进而影响对负荷曲线“削峰填谷”的效果。若电价峰谷差较小，则响应程度过低，难以有效平滑负荷曲线；若电价峰谷差较大，则响应过度，甚至可能出现“峰谷倒置”现象[13]，特别是“大机小网”系统，故对其进行约束：

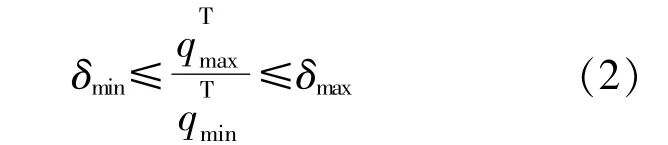
1.2 两阶段优化调度框架

本文整体流程和两阶段优化调度框架如图1所示。

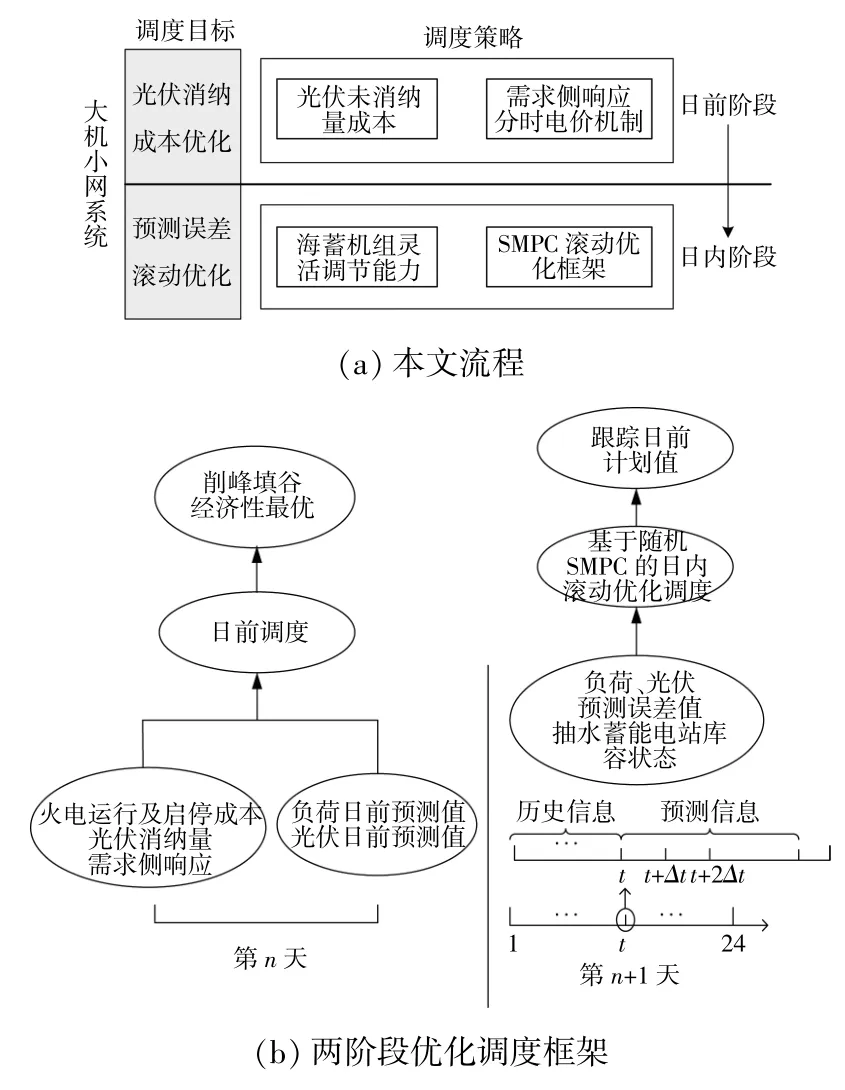
图1 本文流程与两阶段优化调度框架Fig.1 Research flow and two-stage optimal scheduling framework

在日前优化调度阶段，以1 h为调度间隔，采用多种目标加权成本方案，综合考虑了火电运行成本、光伏未消纳量和负荷需求响应补偿成本。其中：火电运行成本考虑了火电机组的运行费用和启停费用；光伏未消纳量利用光伏日前单点预测值来考虑；负荷需求侧响应补偿成本通过分时电价需求响应模型来描述，同时加入了其它相关约束条件。由此，形成了将火电运行成本、光伏未消纳量和需求响应成本加权，以规划周期（24 h）综合指标最优为目标函数的日前调度方案。在日内滚动优化调度阶段，以15 min为间隔、4 h为周期进行滚动优化调度。日内调度以4 h内海蓄机组跟踪日前最优调度结果为目标，在约束中加入海蓄机组启停速率约束，利用SMPC作为实现手段，具体过程：①预测场景集确定，先由预测模型得到优化周期内光伏出力的预测值，再对预测误差的概率密度函数进行抽样得到场景集；②滚动优化，以Δt为周期进行滚动优化，即每Δt进行一次新的优化修正日前计划值，在每次优化中考虑了预测时域内更新后的光伏预测值；③反馈校正，在约束条件下求取整个控制时域内的控制变量值，并下发控制时域内第一个Δt内的控制变量，以求得修正后的调度值，然后在下个周期重复该过程，并对各机组出力值进行实时采样，利用采样实际值进行反馈校正，不断滚动循环。

2 光伏不确定性分析

本文基于光伏预测功率数据，借助场景分析法完成光伏场景的模拟。设t时刻光伏电站实际出力为PPV，它由光伏预测功率和预测误差两部分构成，其表达式为

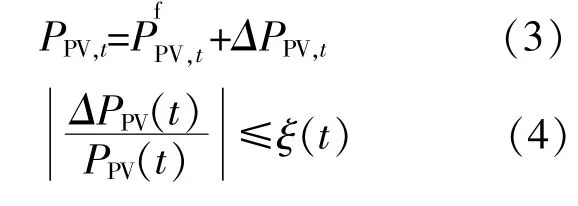
研究表明，光伏出力的相对预测误差随预测时间长度的增加而变大，本文中假设光伏出力预测误差线性增长[14]，即在预测时段内，光伏出力相对预测误差 ξ（t）从第1个时段的20%逐渐增加到最后一个时段的80%。则光伏出力随机模型为

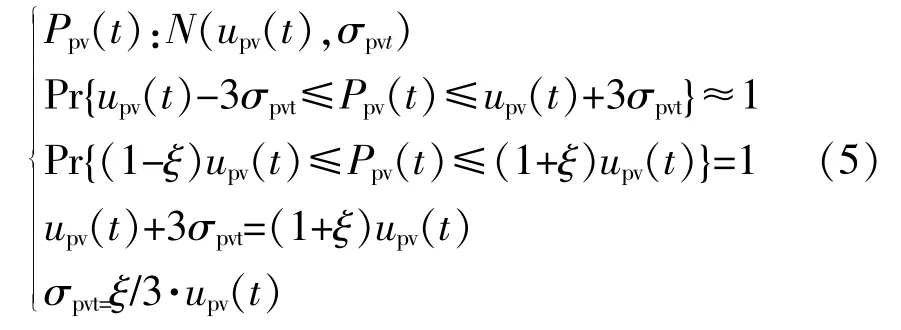
式（5）为光伏实际出力满足以其预测值upv（t）为期望、σpvt为标准差的正态分布。所有正态分布均满足3σ原则。根据式（5）可得到标准差正态分布、相对预测误差和期望值之间的关系。

采用Monte Carlo方法生成若干组光伏预测的随机场景，每种场景都包含未来T时段内的光伏预测值，由此构成初始场景集。由于初始场景集合较大，采用文献[15]场集削减策略对初始场景进行削减，以保证削减后的光伏场景与初始场景的相似度在要求范围内。

3 考虑需求响应的日前优化调度模型

3.1 目标函数

本文构建的日前模型中，期望电网通过合理的调度方案尽量消纳光伏，同时还考虑到系统引入需求响应机制后产生的系统成本和相关收益。本文日前调度选取了火电运行成本、光伏未消纳量和负荷需求响应成本3个调度指标，通过赋予这3个指标合理权重，将它们加权求和得到总目标，从而制定日前火电机组和光伏的发电计划安排。其目标函数分别为

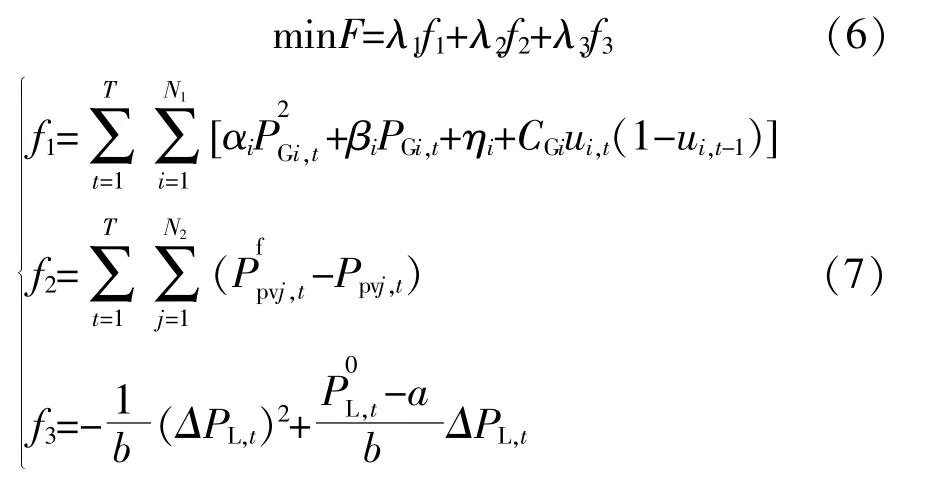
式中：f1为火电机组发电煤耗量；T为优化周期；N1为 火 电 机 组 数；αi，βi和 ηi为 机 组 燃 料 成 本 系 数；PGi，t为机组的发电量；CGi,t为机组的启停成本；ui，t为机组在t时刻的启停状态，0代表停机状态，1代表启动状态；f2为光伏发电未消纳量；N2为光伏电站数；Pfpvj，t为光伏电站在t时的日前发电预测值；f3为系统负荷响应成本；Ppvj，t为光伏在t时的实际发电值；a，b为需求与电价的线性系数；ΔPL，t为系统在引入需求响应后负荷的变化量；P0L，t为系统需求响应前的负荷值；λ1，λ2和λ3为对应的权重系数，本文权重系数的选取以λ1为基准，即λ1=1，λ2取国家标准煤耗量0.320 t/（MW·h），为将系统负荷响应成本折算为等价煤耗量，假定λ3为煤炭价格的倒数，取为0.002 t/元。

3.2 约束条件

①功率平衡约束、火电机组特性约束请见参考 文 献[16]。

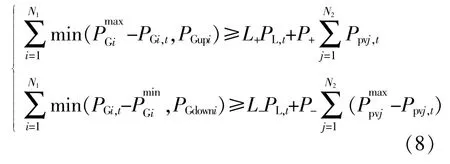
②旋转备用约束式中：PL，t为t时刻系统引入需求响应后的总负荷；P，P分别为机组有功出力的上下限；PGupi，PGdowni分别为机组的上、下爬坡速率；L+，L-，P+，P-分别为负荷和光伏出力的正、负旋转备用系数。

③需求响应约束

需求响应通过改变用户用电时段，达到“削峰填谷”的目的，在调度模型中可视为虚拟发电机组。与常规发电机组类似，某时刻负荷的最大可削减量约束和爬坡约束分别为

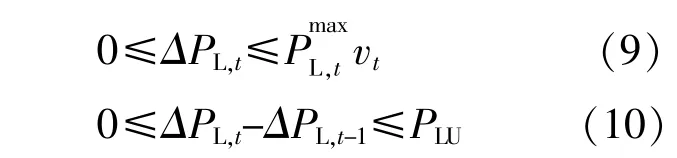
整个调度周期的负荷削减量上限约束为

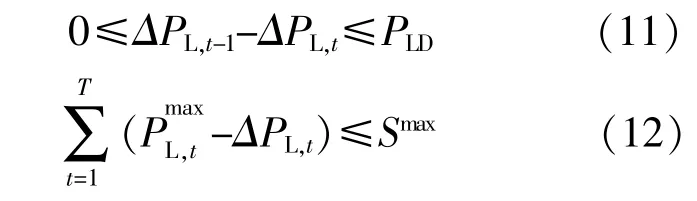
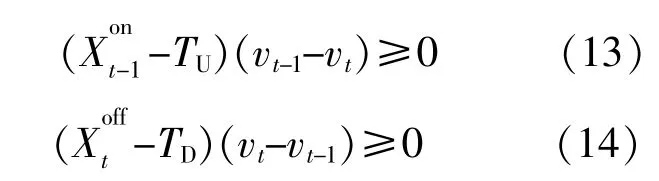
4 基于SMPC的日内滚动优化

MPC的核心是滚动进行有限时域的在线优化，通过某一性能指标最优，确定未来的控制变量。本文在传统MPC的基础上，考虑预测误差，采用SMPC提高系统应对光伏不确定性的能力[10]。通过SMPC将预测误差的概率密度函数进行多场景的选取，即基于光伏预测的概率函数进行抽样，得到能够体现预测误差分布特性的样本集，并通过前文所述方法进行场景削减，最终得到光伏出力的样本序列。

4.1 目标函数

对于日内滚动优化问题，选取火电机组出力、光伏消纳量、海蓄机组出力构成的向量x（k）=[PG（k），Ppv（k），Plg（k）]T为 状 态 变 量，以 火 电 机 组 和 海蓄 机 组 出 力 增 量 构 成 的 向 量u（k）=[ΔPG（k），0，ΔPlg（k）]T为控制变 量，以光伏超 短期预 测功 率 增量 构 成 的 向 量r（k）=[0，0，ΔPpv（k）]T为 扰 动 输 入，则状态空间模型为

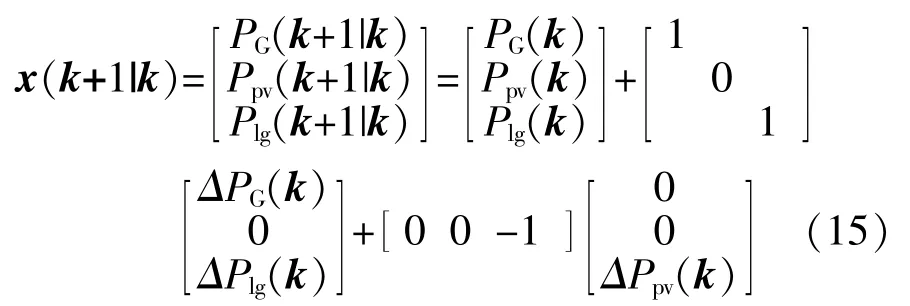
在模型表达式中，默认海蓄机组运行在发电状态时Plg为正值，抽水状态时Plg为负值。基于光伏超短期预测数据，对式（15）反复迭代向前预测p步，便可得到预测输出向量Yf为

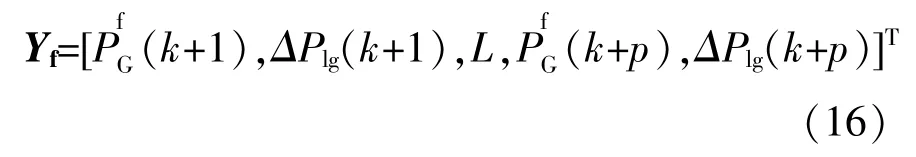
跟踪控制目标向量Pf由日前调度中火电机组出力与光伏预测误差构成，具体表达式为

晋东南旱地春玉米土壤封闭除草剂减量施用效果………………………… 常海霞，杜艳伟，牛 卓，宋艳芳，李娇娇，王建梅（90）

由于滚动优化中时间尺度较小而不改变机组的启停状态，故以火电机组、海蓄机组的预测出力与日前调度计划值之间的误差最小为目标，目标函数为

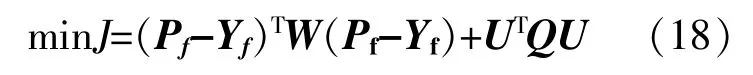
式 中：J为 目 标 函 数 的 取 值；W=diag[WGk+1，Wpvk+1，…，WGk+p，Wpvk+p]为 跟 踪 误 差 权 重 系 数 矩 阵；Q为控制量的权重系数矩阵。

4.2 约束条件

在滚动优化中，海蓄机组能够快速启停，且不需要消耗额外费用，故用其来平衡日前预测误差，在日内优化模型加入海蓄机组相关的约束。

（1）系统功率平衡方程

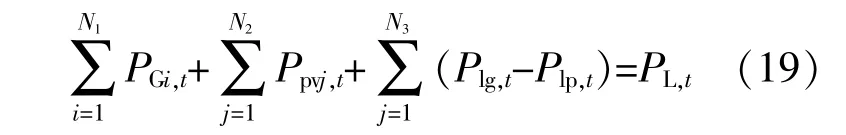
式 中：N3为 海 蓄 机 组 台 数；Plg，t为 第l台 海 蓄 机 组在t时刻的发电功率；Plp，t为海蓄机组在t时刻的抽水功率。

（2）机组出力上下限约束

日前调度里，只有火电和光伏参与运行，但是在日内调度中，对于“大机小网”系统，必须保证在光伏极限出力的情况下火电与海蓄机组仍具有足够的调节能力，故需要对二者出力进行相应约束，它们的上、下限约束分别为

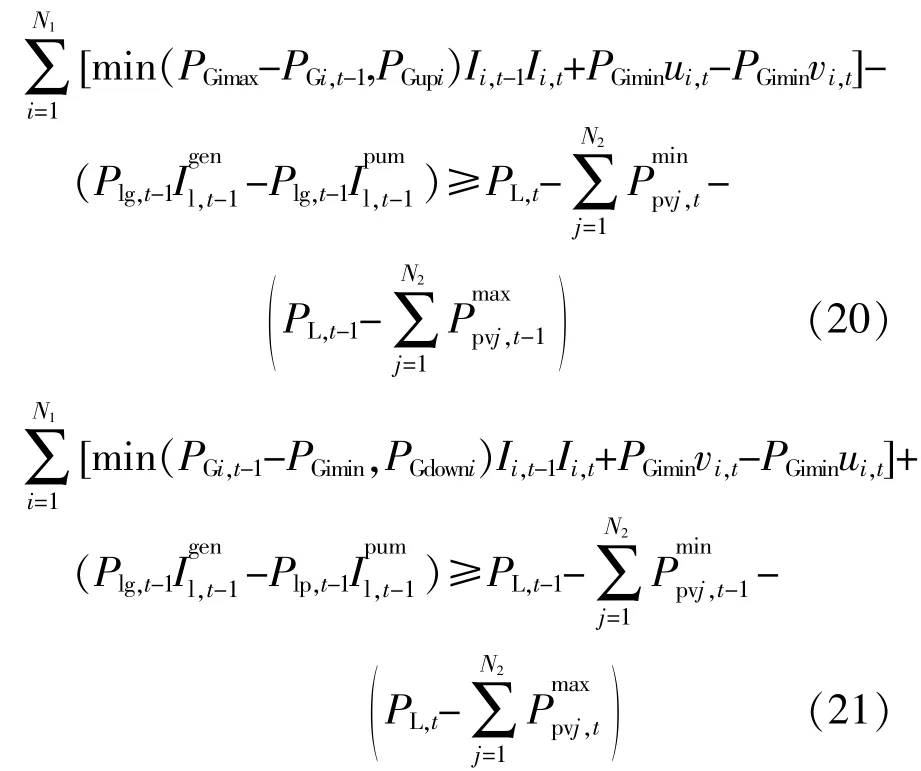
海蓄机组启停速率约束、发电-抽水功率约束、发电功率-水流量平衡及运行工况约束见文献[16]，[17]。

5 算例分析

选取海南某区域电网进行实际算例分析，包括火电机组1台，出力上限为220 MW，下限为120 MW，爬坡速率为10 MW/min，煤耗系数为0.000 4，0.320 0，3.000 0；光 伏 电 站1个，出 力 上 限为50 MW；海蓄机组1台，最大发电功率为60 MW，抽水功率上限为50 MW。

5.1 光伏数据

根据前文的光伏预测场景模拟与削减方法生成光伏预测数据。预测时段为7：00-18：00，以15 min为间隔，借助Matlab软件得到10种典型场景，如图2所示。

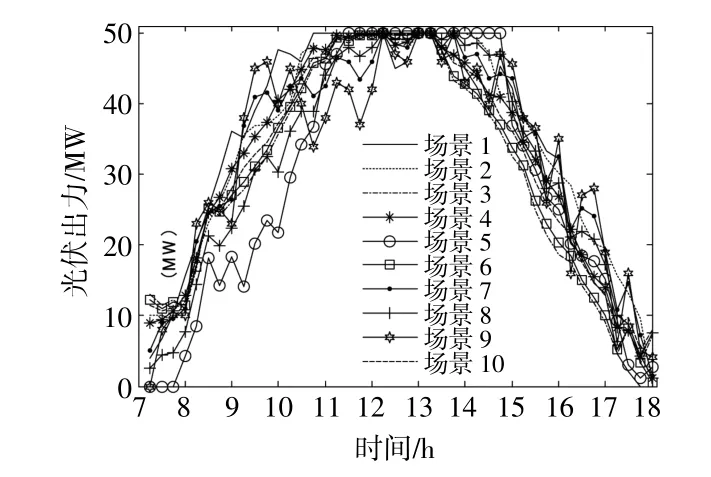
图2 典型光伏出力场景Fig.2 Typical scenarios of photovolataic output

本文分别选取发生概率最大的场景2和光伏波动性最大的场景9，作为光伏日前预测结果和超短期预测结果。日前光伏预测数据以1 h为间隔，故将场景2中每小时内的预测数据平均值作为间隔1 h的光伏预测值，光伏出力预测结果如图3所示。

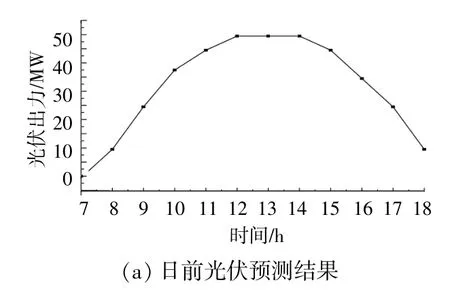
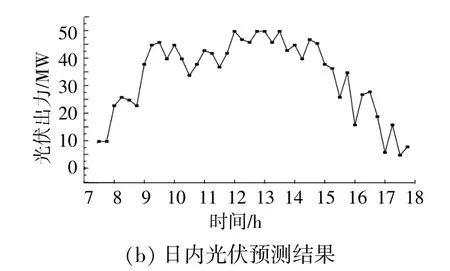
图3 光伏出力预测曲线Fig.3 Photovoltaic output forecast curves

5.2 日前优化调度

针对日前优化调度，设置了3种调度方案来分析不同运行方案对优化结果的影响，如表1所示。方案一：仅考虑火电运行成本与启停速率约束；方案二：考虑火电运行与启停速率和光伏未消纳量；方案三：在方案二的基础上进一步引入需求响应。

表1 3种方案下运行优化结果Table 1 The optimized results of operating cost among different schemes

由表1可知，相较于方案一，方案二和方案三的等价煤耗量分别降低了1.45%和3.16%。

分析光伏未消纳量对日前调度优化结果的影响，如图4所示。

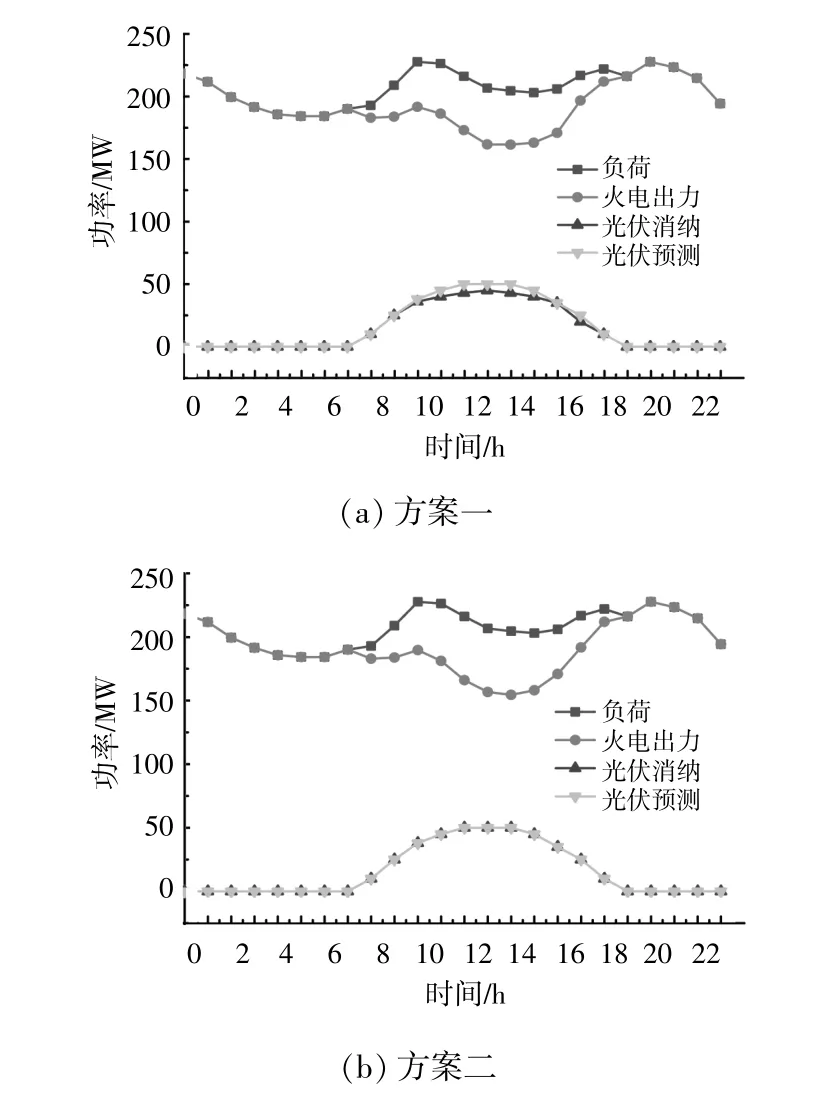
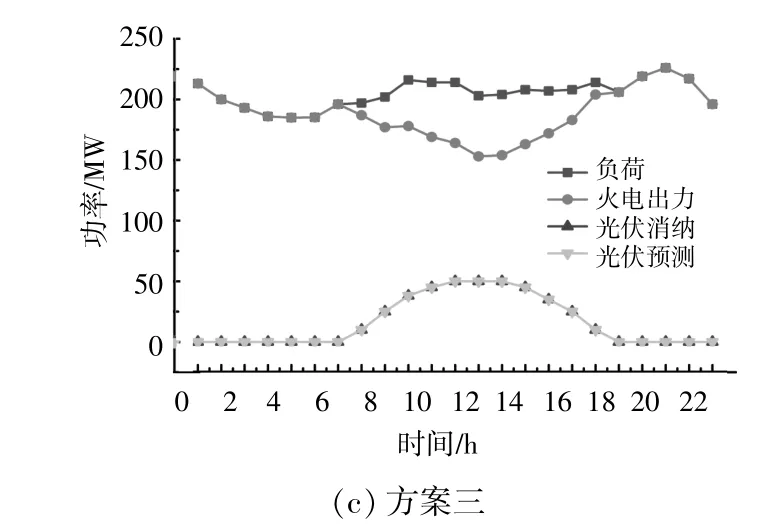
图4 3种方案下日前优化调度结果比较Fig.4 Comparative of day-ahead optimization scheduling results for three schemes

由 图4可 以 看 出：在9：00-17：00，方 案一中的光伏出力未被完全消纳；而在方案二和方案三中，由于目标函数引入了光伏未消纳量的损失成本，光伏消纳量明显增加，且未出现弃光现象，计算可知光伏消纳量提高了10.4%。

图5进一步给出了引入分时电价需求响应模型对典型日负荷曲线的影响结果。

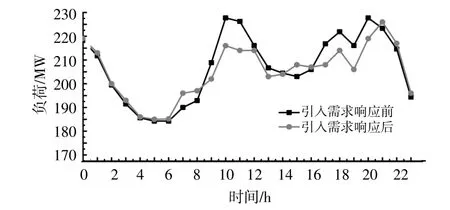
图5 引入需求侧响应前后的日负荷曲线Fig.5 Daily load curves before and after demand response

可见，通过分时电价确实可以引导用户侧的负荷需求，实现了部分负荷从负荷高峰向负荷低谷的转移，从而在一定程度上平滑用电负荷曲线。以上结果说明，本文提出的日前调度方案可提高光伏消纳量，并实现系统运行成本的最优。

5.3 日内优化调度

为考察本文日内优化调度方法的优越性，选取图2中日内光伏发电波动剧烈的典型场景，图6为日前与日内优化调度结果的对比。

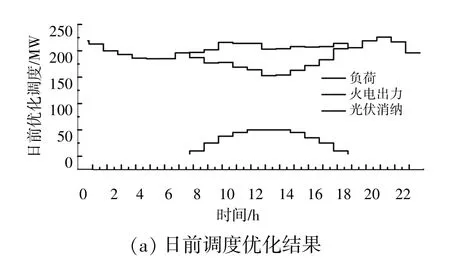
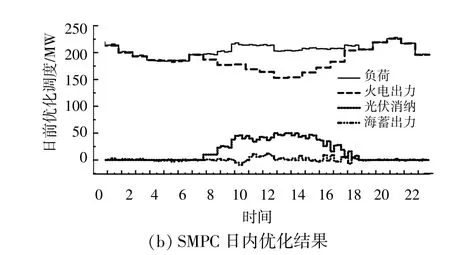
图6 日前、日内两阶段优化调度结果展示Fig.6 Results of two-stage optimal dispatch

由图6可知，SMPC下海蓄机组通过快速地抽水蓄能与发电，有效平衡了光伏预测误差带来的波动，说明SMPC能够解决光伏随机波动带来的“大机小网”功率不平衡问题，并且即使在光伏出力波动剧烈时仍能保证良好的跟踪效果。

6 结论

为解决大规模光伏接入“大机小网”系统的功率不平衡问题，本文提出了日前与日内调度相结合的两阶段火电-光伏-海蓄-需求响应的联合系统运行优化调度方法。该方法在日前调度阶段通过考虑光伏未消纳量损失成本，有效改善了弃光现象，通过引入需求侧响应机制使负荷曲线更加平滑，提高了“大机小网”系统运行经济性。在日内调度阶段采取了随机模型预测控制框架，并考虑了光伏预测的多场景预测误差，通过引入海蓄机组的灵活调节能力，保证了光伏波动剧烈时良好的跟踪效果。