安装于跨海桥梁下部结构的竖轴潮流能水轮机水动力性能研究

2021-03-20何晓宇应永良徐小梅

可再生能源 2021年3期

谢宇，何晓宇，应永良，徐小梅

（1.浙江数智交院科技股份有限公司水运及海洋工程技术研究中心，浙江杭州 310030；2.浙江大学机械工程学院，浙江杭州 310058）

0 引言

近年来，随着我国经济实力的不断提高以及沿海地区经济的快速发展，我国的跨海桥梁技术飞速发展，作为经济发展基础设施的跨海桥梁建设如火如荼。跨海大桥须要跨越海湾或一定海域，因此跨度通常较大，某些可达到20 km或30 km以上。大跨度的跨海大桥在照明、除湿、防腐等方面耗电量较大，且供变电系统也较为复杂。部分跨海大桥连通偏远岛屿，所需能源基本靠外部调入，更是增大了供电系统的复杂性与安装成本。如果可以在跨海大桥建设区域因地制宜的获得电力来源，则可以减少长距离供电设施的建设成本，提高跨海大桥项目的环境友好性，并可为附近岛屿输送电力。

潮流能是海水在涨落潮周期运动中所携带的流体动能，具有和潮汐现象类似的周期性特点，其在某一区域的大小和方向可以较为精确地预测。对潮流能的开发主要是通过在水中布设水轮机等装置将水流动能转化为电能。我国的潮流能储量丰富，近海理论蕴藏量超过8.33 GW，但空间分布很不均匀。其中，浙江省沿岸最为丰富，约为5.19 GW，占我国潮流能资源蕴藏量的50%以上，主要集中于杭州湾口和舟山群岛海域；其次是山东、江苏、海南、福建和辽宁，蕴藏量共计2.98 GW，约占全国蕴藏量的36%[1]。潮流能发电装置须要安装于潮流能富集海域才可以获得良好的电力产出。目前，有较多已建或拟建的跨海大桥通过潮流能富集区，如浙江省是我国拥有跨海大桥最多的省份，跨海大桥数量约占全国的1/3[2]，其中，舟山各岛屿间的连岛跨海桥梁及杭州湾跨海桥梁等多位于潮流能富集区。将潮流能发电装置安装于桥梁结构上，则既可以节省潮流能发电装置支撑结构的建造成本，又可以就地利用潮流能资源为跨海大桥和跨海大桥临近地区提供电力，获得良好的经济与环境效益。目前，将潮流能水轮机与跨海桥梁组合已有一些实践尝试，如荷兰Tocardo公司利用斯凯尔特河防风暴桥桥桩安装水平轴潮流能发电阵列（图1）[3]，大连理工大学借助长海县长山大桥施工附属结构安装的同轴双转子机组（图2）[4]，[5]。

图1 安装在桥梁结构上的水平轴潮流能发电阵列Fig.1 The horizontal-axis tidal current turbine array mounted on the bridge

图2 安装在长山大桥附属结构上的竖轴同轴双转子机组Fig.2 The vertical axis coaxial dual rotor turbine installed on the auxiliary structure of Changshan Bridge

跨海桥梁下部结构通常具有很大的截面尺寸，会明显改变周围流场。当潮流能水轮机安装于桥梁下部结构时，桥梁结构对流场的扰动可能会对水轮机的水动力性能产生明显影响。竖轴水轮机旋转轴与来流方向垂直，当桥梁下部结构不采用斜桩时，水轮机旋转轴与下部结构轴线平行，可以较为方便地将竖轴水轮机同下部结构并列布置。由于竖轴水轮机的运行不受来流方向影响，当布置在桥梁下部结构附近时，将对附近流场的变化有良好的适应性。目前，对潮流能发电装置的研究主要集中在单机水动力分析或水轮机与导流涵道相互作用分析上，尚未见到针对竖轴水轮机与桥梁下部结构组合后水动力变化情况的研究或相应的工程实例[6]，[7]。为了对这一技术的工程应用前景进行讨论，本文通过数值模拟和物理模型实验相结合的方式对竖轴水轮机与几种典型桥梁下部结构形式组合的情况进行分析，研究竖轴水轮机在此种情况下水动力性能的变化情况，并考虑水轮机与下部结构的相对尺寸变化所带来的影响。

1 桥梁下部结构形式及研究工况选取

桥梁通过下部结构承担桥梁上部结构所产生的作用，并将作用有效地传给地基。架设长度较长的跨海桥梁，通常采用“桩基础+桥墩（台）+桥台”的下部结构形式。下部结构中，常处于水面以下的是桩基础和墩台结构。竖直单桩或多桩基础，或具有圆弧迎流截面且壁面垂直的墩台是安装竖轴水轮机的理想位置。本文对竖轴水轮机安装于单圆桩基础、四圆桩基础和圆端形墩台的情况进行分析。这一类下部结构形式已在位于潮流能富集区的跨海桥梁上有较多应用，如在引桥段采用单圆桩基础的鱼山大桥[8]，[9]；采用四圆桩基础的长山大桥[10]、杭州湾跨海大桥[11]等；圆端形墩台则是桥梁墩台的常见方案。为了避免桥梁下部结构出现扭转力矩，将竖轴水轮机在桥梁下部结构两侧对称布置且旋转方向相反。如图3所示，为使初始条件一致，根据实际桥梁常采用的设计方案对3种桥梁下部结构形式的迎流面宽度进行统一。图中：桩基础和墩台整体迎流宽度为2R′；单圆桩情况下，圆桩半径为R′；四圆桩时，圆桩半径为r，且R′=3.5r，4个圆桩在四角内切于边长为2R′的正方形；圆端形墩台两端的弧形曲面为半径为R′的半圆，半圆间直线段长度为2R′；竖轴水轮机为一典型三叶片形式，叶片弦长为c，半径为R，且c=0.26R；水轮机与桥梁下部结构的间距为d，d的取值过大会引起水流能量的损失且增大连接机构的成本，取值过小则无法保证水轮机的安全运行，经过综合考虑，令d=0.6c。

图3 水轮机与下部结构的布置示意图Fig.3 The illustration of the arrangement of the turbine and the substructure

为了确保桥梁安全，竖轴水轮机对桥梁下部结构的荷载应低于某一限值。这一限值与桥梁自身属性有关，配套水轮机时，应根据这一荷载限值确定水轮机尺寸。本文对不同尺寸比例的水轮机与下部结构的组合情况进行分析，定义尺寸比α为

因此，当 α确定时，图3中各部分结构的几何尺寸关系可以唯一确定，后续将在单圆桩、四圆桩和圆端形墩台中以 α的不同取值划分研究工况，α的取值为0.7～1.3。

2 数值模型建立与实验方案设计

使用目前广泛应用的商业CFD软件Ansys Fluent进行二维数值模拟。在数值模型中，竖轴水轮机为三叶片NACA0018翼型，水轮机半径R取为2.5 m，各工况建模时R保持不变，根据相应的 α取值确定其他几何参数的数值。计算域垂直流向方向的长度为50R，顺流向方向的长度为40R，上游边界采用速度入口，入口流速为2 m/s，下游边界为出口，其余外部边界为对称边界，水轮机叶片和结构物壁面设为无滑移墙，整体的计算域和边界设定如图4所示（以单圆桩情况为例）。

图4 计算域和边界条件设定Fig.4 Computational domain and boundary condition settings

为了模拟水轮机转动，设定一包裹水轮机的圆形区域为旋转域，采用滑移网格方法使旋转域以指定速度旋转来模拟水轮机运转。按图3所示情况的定义，左侧水轮机逆时针旋转，右侧水轮机顺时针旋转，开敞情况时水轮机顺时针旋转。为了保证计算精度，对水轮机和结构物以及流态剧烈变化区域的网格进行加密，各工况均采用相同的设置参数进行网格划分，整体网格数量约为55万。采用Pressure based求解器进行数值模拟计算。由于k-εRealizable湍流模型在计算流动分离、边界层流动方面的良好表现[12]，[13]，湍流模型采用k-εRealizable湍流模型，并配合scalable wall functions壁面函数。控制方程中的动量离散项采用二阶迎风差分格式，压力离散项采用二阶中心差分格式，湍动能和湍流耗散率选用一阶格式。

小比尺物理模型实验在浙江海洋大学的船舶拖曳水池（长130 m，宽6 m，水深3.5 m）中进行，对单圆桩，α取值分别为0.9，1.0和1.2的工况进行实验。图5为实验装置示意图。实验模型采用重力相似准则设计，长度比尺为10，即水轮机模型的半径为0.25 m。水轮机输出轴向上通过直角换向器改为水平旋转后，依次连接转矩转速传感器和磁粉制动器。在每一工况的实验中，通过磁粉制动器来调节水轮机负载，进而控制水轮机转速，使之处于所需要的运转尖速比位置。转矩转速传感器可以实时监控水轮机转速及负载大小，并记录水轮机的输出功率变化情况。对应工况实验结束后，可根据记录的水轮机输出功率及水轮机尖速比情况，绘出水轮机输出功率随尖速比变化的曲线。

图5 实验装置示意图Fig.5 The illustration of experimental devices

3 结果与分析

数值模拟过程中，假定水轮机转动过程中的转速恒定无脉动。定义无量纲量尖速比λ为

式中：ω为水轮机旋转角速度，rad/s；R为水轮机半径，m；V为水流的来流速度，m/s。

定义水轮机的获能系数Cp为

式中：P为水轮机的输出功率，W；ρ为流体密度，kg/m3；L为水轮机的迎流截面面积，m2；在二维情况中，L为迎流截面宽度，m。

在每一工况的模拟中，水轮机的尖速比均为1.25～3.75。从尖速比1.25开始计算并逐渐升高转速，直至设定的尖速比上限为止。在每一尖速比的计算中，待水轮机运行稳定后，提取水轮机的平均功率并计算当前尖速比对应的Cp值。在开敞条件下，竖轴水轮机的Cp随尖速比的变化情况如图6所示。

图6 开敞情况下，水轮机的Cp随λ的变化情况Fig.6 The variation of Cp of the turbine withλin open water

由图6可以得到水轮机在开敞情况下所能达到的Cp最大值。在每一工况的计算中，均按照这一方法提取水轮机在这一工况下的Cp最大值，以进行各工况间的横向比较。为了比较各工况中水轮机最大Cp相对开敞时的变化情况，定义获能系数变化比Cr为

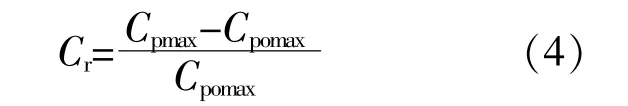
式中：Cpmax为相应工况中水轮机Cp的最大值；Cpomax为开敞情况下水轮机Cp的最大值。

整理得到各工况下的Cr值，如图7所示。

图7 Cr随α的变化情况Fig.7 The variation of Cr withα

从图7中可以看出，单圆桩情况的数值模拟结果与物理模型实验结果吻合较好，两者的变化趋势相一致，数值模拟结果略高于物理模型实验结果。造成这种差异的原因：实验过程中传动部件造成的能量损失；相比二维情况，实验中的竖轴水轮机和圆桩的垂向长度有限，在边缘处存在能量耗散。总体来看，本文所采用的数值模拟方法可以较为准确地反映竖轴水轮机的水动力性能变化情况。从图7还可以看出：将竖轴水轮机与任一形式的桥梁下部结构组合均能够提升竖轴水轮机的能量输出，其中，单圆桩提升幅度最大，圆端形墩台次之，四圆桩最小；水轮机与单圆桩和圆端形墩台组合时，Cr随着 α增大而逐渐减小，而水轮机与四圆桩组合时，Cr则随着 α增大而逐渐增大。

图8为不同工况下的流场速度云图。

图8 流场速度云图Fig.8 The contour of velocity magnitude

从图8可以看出，竖轴水轮机受到了结构物迎流面两侧高流速区的作用。结合图7和图8可以看出：单圆桩和圆端形墩台的迎流截面较长，导向水轮机的能量更多，因此，单圆桩和圆端形墩台的Cr值远大于四圆桩的情况；随着 α的增大，单圆桩和圆端形墩台相对水轮机的尺寸缩小，使得导向水轮机的能量减少，进而导致水轮机的Cr降低；在四圆桩情况中，当 α较小时，水轮机受到了上游圆桩尾流的影响，当 α增大时，虽然圆桩截面减小，但圆桩两侧的高流速区域对水轮机的影响逐渐增大，使Cr值缓慢增加。从结构迎流（阻水）宽度的角度来说，单圆桩和圆端形墩台的迎流宽度为2R′，四圆桩的迎流宽度为4r，根据前述定义R′=3.5r，因此，当尺寸比相同时，两者的迎流宽度之比为7∶4。如果以迎流宽度为变量，水轮机的Cr将延续图7中的变化趋势，只是在进行结构迎流宽度比较时，须将四圆桩曲线向右侧偏移至相应位置。

在实际海域中，潮流流向通常往复变化。当流向反向时，水轮机相对结构物的转动方向也随之改变。对部分工况的反流向情况进行计算，由于正流向时，Cr随 α基本呈线性变化，反流向计算时，只选取α=0.7和 α=1.3的情况，所得Cr的结果如表1所示。由表1可以看出：反流向时，水轮机的获能也有明显的提升，且随α的变化趋势与正流向一致；水轮机的获能略低于正流向情况，但总体上差距不大。

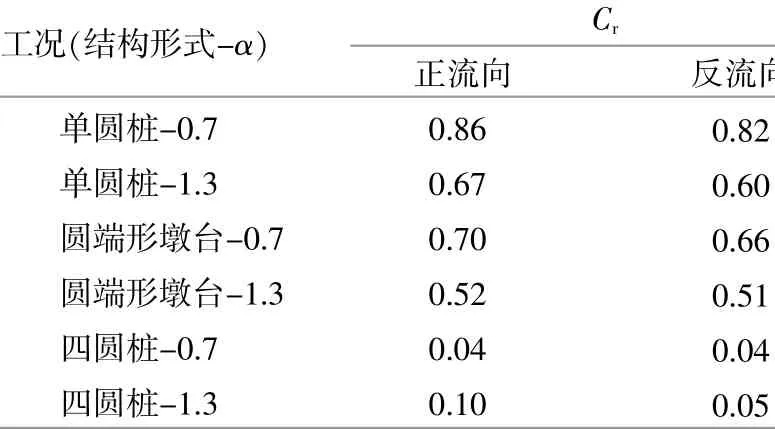
表1 部分工况正反流向的Cr对比Table 1 Comparison of Cr in different flow directions

为了进一步研究水轮机输出功率的变化机理，对不同工况中水轮机在最大获能尖速比时单个叶片沿圆周方位角的获能情况进行分析。提取单个叶片在不同圆周位置转动时所受的转矩，定义无量纲量转矩系数CT为式中：T为水轮机叶片对中心旋转轴的转矩，N·m；A为水轮机叶片的横截面积，m2。

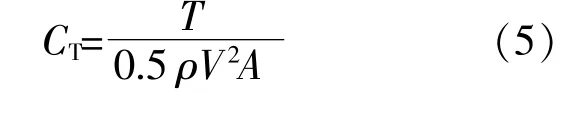
由于不同工况中水轮机取得最大能量输出的尖速比并不一致，定义无量纲量Cps为水轮机单个叶片的尖速比与相应叶片转矩系数的乘积，则Cps可以表征水轮机单个叶片在不同尖速比（TSR）运转状态下的获能情况。Cps的计算式为

对于竖轴水轮机与单圆桩、圆端形墩台和四圆桩组合的情况，当 α=1时，提取水轮机在最大获能尖速比运转时的相应数据计算单个叶片的Cps值，并按叶片相应方位角位置绘出，即可得到叶片的Cps沿圆周方位角的分布情况（图9）。水轮机为结构物右侧的水轮机，相对位置参考图3。图9中，不同半径的虚线圆圈代表Cps的大小，图例曲线在相应圆周方位角处与圆心的距离即为叶片在该方位角处的Cps值。

图9 典型工况中水轮机的获能尖速比最大时，Cps沿圆周方位角的分布Fig.9 CpsVS azimuth in max energy-obtained TSR in typical conditions

由图9可以看出，Cps存在负值区域，当叶片处于Cps负值区域时，对水轮机旋转起阻碍作用。在开敞情况下，竖轴水轮机的获能区域主要在上游±50°方位角范围内。当竖轴水轮机与下部结构组合后，竖轴水轮机的获能区域范围扩大，且幅值上升，因而提高了水轮机的整体能量输出。比较单圆桩与圆端形墩台情况可知，单圆桩时的获能范围更宽，且偏向于左侧圆桩位置，这是因为单圆桩的圆弧迎流面更靠近水轮机，高流速区对水轮机的影响更为显著，使得水轮机与单圆桩结合时的能量输出大于圆端形墩台情况。在圆端形墩台情况中，若将水轮机安装位置向上游方向偏移，使其更靠近圆端形墩台的圆弧迎流面，则水轮机的能量输出可进一步提升甚至接近单圆桩情况；但当潮流流向反向时，由于水轮机与上游的圆弧迎流面距离增加，其能量输出将减少。为了使水轮机在往复流向中的性能较为均衡，通常将水轮机安装在圆端形墩台中部。