First-principles analysis of phonon thermal transport properties of two-dimensional WS2/WSe2 heterostructures∗

Zheng Chang(常征), Kunpeng Yuan(苑昆鹏), Zhehao Sun(孙哲浩), Xiaoliang Zhang(张晓亮),†,Yufei Gao(高宇飞),‡, Xiaojing Gong(弓晓晶), and Dawei Tang(唐大伟),¶

1Key Laboratory of Ocean Energy Utilization and Energy Conservation of Ministry of Education,School of Energy and Power Engineering,Dalian University of Technology,Dalian 116024,China

2Institute of Materials Science and Engineering,National Experimental Demonstration Center for Materials Science and Engineering,Changzhou University,Changzhou 213164,China

Keywords: WS2/WSe2 bilayer heterostructures,thermal transport,first-principles,Boltzmann transport equation

1. Introduction

Transition metal dichalcogenides(TMDCs)have rapidly emerged and attracted tremendous interests in the microelectronic industry due to their innovative physical properties and many applications in devices. Their composition is usually expressed as MX2(M,transition metal element and X,chalcogen element), which can exist stably as monolayer, bilayer,and bulk crystal structures. Different from graphene, twodimensional (2D) TMDCs materials, which have wide band gap and high electron mobility,can be seen as excellent candidates for semiconductor and optoelectronic devices.[1-4]Each transition metal atom layer in the 2D TMDCs material is sandwiched between two chalcogen atom layers,and their stability of in-plane direction is maintained by the covalent bonds. In contrast, the van der Waals interaction in the out-of-plane direction is relatively weak which can be sufficient for individual 2D crystals to keep free-standing.[1,5]Nowadays,a variety of 2D TMDCs materials, such as single-layer WS2, WSe2, etc.,have been produced by chemical vapor deposition method[6,7]and extensive attempts have shown that the 2D TMDCs can be seen as one of the most promising thermoelectric materials at relatively high temperatures.[8,9]

Most recently,various thermoelectric materials have been designed for converting waste heat to electricity(Seebeck effect). The figure of merit(ZT)is used to evaluate the performance of thermoelectric materials based on ZT =S2σT/κ,which refers to the Seebeck coefficient (S), electrical conductivity (σ), and thermal conductivity (κ). The total thermal conductivity (κ) consists of electronic thermal conductivity (κel) and lattice thermal conductivity (κlat). Combining with the equation of ZT, it can be noticed that high S,high σ, and low κ are preferred to improve ZT.[10]Furthermore, anisotropic single-layer crystals[11]are also supposed to have high ZT[12]comparing with bulk crystals. Nevertheless, the occurrence is not noticeable in the 2D WX2(X = S, Se) crystals.[13]Heterostructures (e.g., WS2/WSe2-BHs,MoS2/MoSe2-BHs)have attracted significant interest for their smaller band gap than those of single-layer MoS2and MoSe2,[14]especially in the energy storage fields.[15-18]

It has been reported that the WS2/WSe2-BHs has concentrated on the arrangement of the density of states around the Fermi level and band gap.[19]The WS2/WSe2-BHs shows a reduced band gap compared to those of 2D WS2and WSe2.It is generally accepted that alteration of the electronic band structure could be ascribed to the change of the weak vdW interaction.[14]In addition, for 2D WX2(X = S, Se) crystals, constructing heterostructure is an effective approach to enhance ZT because combining single-layer nanocrystals is an effective way to increase phonon anharmonicity.[20]Generally,a high ZT value is required by high performance thermoelectric materials and the reduction of κlatis also necessary.[21-23]Despite the electronics of the WS2/WSe2-BHs have been reported in recent years,[14]there is little quantitative analysis of their phonon transport properties until now.

The purpose of this paper is to investigate the phonon transport in the WS2/WSe2-BHs and theoretically explore alteration of phonon transport properties, which is attributed to the interlayer vdW interaction,by using first-principles calculations based on the density functional theory(DFT)together with an iterative solution of the phonon Boltzmann transport equation (BTE). In order to further reveal the difference of phonon transport mechanisms between the WS2/WSe2-BHs and single-layer WS2and WSe2,we also calculated and studied the charge transfer across the interface and representative phonon mean free paths(MFPs)of the WS2/WSe2-BHs.

2. Model system and computational methodology

2D TMDCs emerge 2H phase(hexagonal symmetry)with the MX2, where M represents W or Mo; X represents Te, Se,or S.The WS2/WSe2-BHs,including a single(S/Se)-W-(S/Se)layer with space group P¯6M2(No.187), which has no inversion symmetry and is shown in Fig.1.On the vertical direction of the WS2/WSe2-BHs,the Se and W atoms at the bottom are completely overlayed by the W and S atoms at the top,respectively. The optimized lattice parameters of the WS2/WSe2-BHs formed as hexagonal structure are a=b=3.53 ˚A, and interlayer distance d = 3.53 ˚A ties well with previous theoretical calculations.[14,24]Considering the lattice mismatch can lead to stack disorder or Moir´e pattern superstructures,we also calculated its intrinsic lattice mismatch δ (δ ＜±5%)with δ =100%×(a1−a2)/a2,where a1and a2are the lattice parameters of 2D WS2and WSe2, respectively. The calculated value of δ =−3.7%is in good agreement with previous studies,[24,25]and proves the stability of the WS2/WSe2-BHs.

The crystal structure of WS2/WSe2-BHs has been optimized by first-principles calculations within the framework of DFT,as employed in the Vienna ab-initio simulation package(VASP).[26]The Perdew-Burke-Ernzerhof (PBE) functional with generalized gradient approximation(GGA)[27]is adopted to describe the electron exchange and correlation functional.The planewave cutoff energy and k-point sampling are set to be 550 eV and 11×11×1 grid within Monkhorst-Pack[28]scheme, respectively, and the energy convergence threshold is set as 10−6eV. The effect of vdW interaction is considered in all simulations with dispersion corrected DFT method(vdW-DF-revPBE),[29]which has been proven reliable for the vertically stacked system.[30]Moreover, we imposed a vacuum spacing larger than 20 ˚A to avoid the interactions among heterostructures neighboring layers in the periodic slabs. All atoms in the crystals system are fully relaxed until Hellmann-Feynman force on each ion is less than 10−4eV·˚A−1.

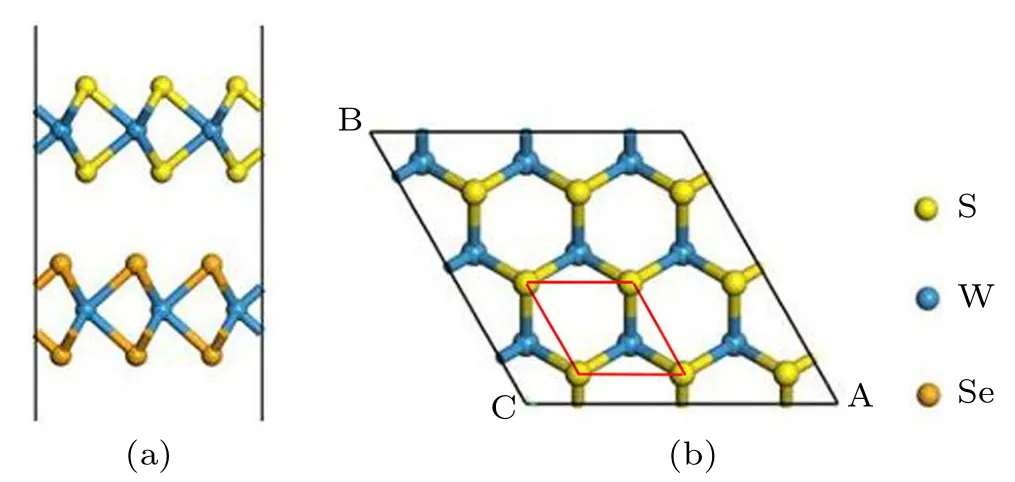
Fig.1. Optimized crystals structure of the WS2/WSe2-BHs. (a)Local side view and(b)top view.

The klatof a material can be computed by solving the linearized BTE for phonons, as employed in the ShengBTE code.[31,32]It can be expressed as

where να(qs)represents the phonon group velocity along the α-th direction, τqsrepresents the phonon lifetime, q and s denote the wave vector and branch index of specific phonon mode,respectively. Cν(qs)refers to the heat capacity at constant volume for each phonon mode, and it can be written as

We first calculated the phonon dispersion of the WS2/WSe2-BHs and used 3×3×1 supercell containing 54 atoms. The Γ point mesh of 1×1×1 is applied to sample the BZ.The density functional perturbation theory(DFPT)as applied in the VASP code[26]is used to compute harmonic second-order interatomic force constants (IFCs). Then, the phonon dispersion within the frozen phonon approximation and phonon density of states (PhDOS) are also computed by using the PHONOPY code.[33]Considering the existence of long-range electrostatic interactions of the polar materials,non-analytical terms are added to the dynamical matrices,and the corresponding parameters,including Born effective charge tensor and the dielectric tensor,are obtained from DFPT.With the aim to get the precise value of κlat,anharmonic third-order IFCs are also taken into account. Specifically speaking, the 3×3×1 supercell and 1×1×1 Γ point mesh for calculating anharmonic third-order IFCs are used in the script of the thirdorder.py.[31]For the κlatcalculations, the 90×90×1 of q-grid is used,and it should be well converged for the calculation of κlat.

First-principles-based predictions of κlatfrom perturbation theory have attained significant achievement only considering three-phonon scattering. Furthermore, four-phonon and higher-order processes are multi-phonon processes, and their evaluations have been a long standing and significant challenge for decades.[34]Recently, more and more theoretical results have proved that the effect of four-phonon and higher-order phonon scattering processes are very little in most semiconductors.[35-37]Thus, only three-phonon scattering processes are considered in this paper,and the role of fourphonon and higher-order scattering processes have been ignored.

3. Results and discussion

3.1. Phonon dispersion

For vertically stacking 2D WS2on top of 2D WSe2,the newly formed WS2/WSe2-BHs still holds the 2H phase.Since phonon dispersion curves are crucial for the calculation of phonon transport, the phonon dispersion curves of the WS2/WSe2-BHs along some high symmetry lines and Ph-DOS are plotted in Fig.2. The WS2/WSe2-BHs unit cell has six atoms resulting in eighteen phonon branches. As shown in Fig.2, one notable information in the phonon dispersion curves is a small gap between the lowest optical mode and the highest acoustic mode. Since vdW forces hold WX2(S, Se)single-layers together in the WS2/WSe2-BHs, the vdW force assists in stabilizing the WS2/WSe2-BHs and eliminating the imaginary phonon modes. The k∗theorem theory[38-40]for phonons is applied with sorting the phonon modes of the WS2/WSe2-BHs under the continuousness of their eigenvectors,and it can be expressed as

In crystals,the potential energy Φ is assumed to be an analytic function of the displacement(r)of the atoms.[41]When the fully optimized crystal structure is stable,its potential energy continuously increases against any mixtures of atomic displacements. Specifically, a mechanically stable crystal needs to obey the equilibrium,∂Φ/∂r=0.The phonon modes with their color weighted for the contribution of W, Se, and S atoms have been calculated to ensure that the fully relaxed crystal of the WS2/WSe2-BHs is located at a minimum on the potential energy surface. All the phonon modes together with their widths are weighted in the qualitative representation characteristics of vibration modes including the contribution of atoms and their direction and amplitude,named fat bands.

The fat bands for W(xy),W(z),Se(S)(xy),and Se(S)(z)vibrations are displayed in Figs.2(a)-2(c),and the corresponding PhDOS of the WS2/WSe2-BHs is shown in Fig.2(d).The absence of phonon modes with negative frequencies indicates that the WS2/WSe2-BHs is dynamically stable at 0 K.It also worth to mention that there are hybridizations among the W(xy)and W(z)vibrations for quite a few phonon modes,while these optical modes above 10 THz almost express no vibrations in Fig.2(a). The non-orthogonality of the covalent W-Se and W-S bonds can result in the W(xy-z) hybridization. Moreover, it is crucial to highlight that the Se(z) vibration occupies the main percentage closing to within the Γ point signified by the black circles in Fig.2(b).This hybridization is consistent with the consequence of 2D WS2, which is caused by the singular interlayer crystal symmetry.[39,42]The layer of W atom is sandwiched between two S(Se)layers for the WS2/WSe2-BHs, which makes the xy direction and z direction vibrations of the W atom layers be independent from each other. Further, combining with the projected PhDOS plotted in Fig.2(d), it is worthwhile mentioning that the W atoms are to be occupied by important parts at all the different phonon modes. However, the Se (S) atoms play a dominant role in medium low frequency(5-8 THz)and high frequency(8-12 THz) areas, respectively. More interestingly, there are several peaks in the optical phonon modes region,which indicates the smaller phonon group velocity.

Both harmonicity and anharmonicity of phonon show close relationship with the klat. The phonon group velocity is an important parameter to describe the phonon harmonicity. To fundamentally understand the mechanisms of the klatchanged from 2D WS2, the WS2/WSe2-BHs to 2D WSe2, the phonon dispersion curves of the above models are calculated. The calculated phonon dispersion curves of 2D WS2, 2D WSe2, and WS2/WSe2-BHs are plotted in Figs. 3(a)-3(c). From these figures, we also observe that both 2D WS2and WSe2have three acoustic modes, i.e., two linear acoustic modes[one transverse(TA1),one longitudinal (LA1)] and one quadratic flexural acoustic branch (ZA1). The TA1and LA1display linear dependences closing to the Γ point, which is accordance with the previous works.[43,44]As the symmetry in the crystal structure is the same,there is great similarity for phonon dispersion curves of the 2D WS2and WSe2except for comparatively higher phonon frequencies of 2D WS2. The reason is that the mass of Se(78.96 amu,1 amu=1.660539×10−27kg)is much heavier than that of S(32.065 amu). Meanwhile,the average Debye temperature(TD)is defined by[45]

Fig.2. (a)-(c)Phonon dispersion curves with fat bands indicating movements of atomic vibrations and(d)PhDOS of the WS2/WSe2-BHs.

As for the WS2/WSe2-BHs, it has another three low frequency optical modes, defined as ZA2, TA2, and LA2. In Fig.3(c), it can be also observed that the LA1and ZA2intersect with each other, which results in the changing shape of LA1. Closing to the kinks, the LA1branch becomes softened, which means the reduction of phonon group velocity.These phenomena have also been found in the other bilayer structures, which can be seen as the effects of the weak vdW interaction.[10,46,47]

Fig.3. Phonon dispersion curves of the acoustic and relatively low-lying optical phonon modes alongside the high symmetric path Γ-M in the BZ for(a)2D WS2,(b)2D WSe2,and(c)WS2/WSe2-BHs.

3.2. Lattice thermal conductivity

Recently,the previous review has illustrated that the cutoff of anharmonic interaction is the key to the computation of the κlat.[48]While too large cutoff radius usually leads to much more computational resources, a small cutoff may overestimate the value of κlat. Therefore, the convergence of the κlatwith regard to the cutoff radius of anharmonic IFCs should be investigated firstly. Qin and Hu recently proposed that[49]based upon the analysis of harmonic IFCs, the cutoff radius can be directly determined to gain the acceptable value of κlat. To better understand the strength of the interatomic interactions, the normalized trace of IFC tensors needs to be computed.[50]According to this parameter, we can directly determine how large the cutoff radius would be to quantitatively assess the anharmonic IFCs by the meaning of containing the strength of this probably strong interactions as exposed by the large trace value. It can be clearly seen in Fig.4(a) that the reasonable cutoff is a distance of 0.72 nm,and over 9thnearest neighbors have extremely weak trace values, representing negligible anharmonic IFCs. As proved for the convergence investigation of the κlatin Fig.4(b), there is a striking drop for the κlatto the rear of taking account for the 3thnearest neighbors and the computed κlatmeets rapidly up to the 9thnearest neighbors. This is consistent with the observation and evaluation from the strength of the harmonic IFCs in Fig.4(a). Guo et al. calculated the value of κlatof the MoSe2/WS2-BHs taking an interaction range of 0.63 nm for the anharmonic IFCs.[51]Hence, taking into account of computational price and accuracy, the interactions up to the 9thnearest neighbors are considered for the anharmonic IFCs computations.

Fig.4. (a)Normalized traces of IFC tensors versus atomic distances and(b)convergence examination of the κlat with regard to the cutoff radius.

Based on the converge test of anharmonic IFCs, we plot the computed κlatof 2D WS2,WSe2,and the WS2/WSe2-BHs as a function of temperature ranging from 200 K to 1000 K in Fig.5(a),the κlatof these three systems decrease continuously with increasing temperature. In Table 1, we have listed the computed values of κlatfor 2D WS2and WSe2together with the WS2/WSe2-BHs at RT. For 2D WSe2, the lattice thermal conductivity,about 46.8 W/mK,is close to one half of that of 2D WS2. For comparison, some results of previous studies are also shown in Table 1.[8,42,44,52-54]It should be pointed out that our calculated results for the 2D crystals are in accordance with the previous theoretical calculations[54]and experimental measured[53]data. Our calculated lattice thermal conductivities of 2D crystals are a little higher than the experimental measured values due to the lack of impurity,defect,and edge as scatters in our model. Combining our calculation, we obtain κlatof 62.98 W/mK for WS2/WSe2-BHs at RT, which is between those of single-layer WS2and WSe2. Furthermore,it is slightly lower than the average κlatvalue(74.27 W/mK)of single-layer WS2and WSe2.

Fig.5. (a)The computed κlat versus temperature for WS2/WSe2-BHs,2D WS2,and 2D WSe2. (b)The cumulative κ versus the frequency for WS2/WSe2-BHs. The low frequency range(＜4.73 THz)is scratched in blue.

In order to deeply explore and understand the major heat carriers of the WS2/WSe2-BHs, we have calculated the normalized cumulative lattice thermal conductivity κ as a function of phonon frequency at 300 K,500 K,700 K,and 900 K,as shown in Fig.5(b). It can be noticed that the phonon branches with a frequency lower than 4.73 THz contribute nearly 90%to the κlat,which indicates that the three acoustic branches and some low lying optical branches play a dominant role in the heat transport of the WS2/WSe2-BHs.

Table 1. Calculated in-plane κlat of 2D WS2 and WSe2 along with the WS2/WSe2-BHs at RT.

Some previous work reported κlatof 2D materials with sample length around 10 µm long or sufficiently large spans about three orders of magnitude.[42,55,56]We have calculated the κlatof the WS2/WSe2-BHs, 2D WS2, and WSe2as a function of temperature for several sample lengths and infinite length for comparison, as shown in Fig.6. It can be noticed that the κlatdecreases with decreasing sample lengths of the studied model structures because of increased phononboundary scattering. For the cases of the length being 10µm,1 µm, and 0.1 µm, the 300 K lattice thermal conductivity of the WS2/WSe2-BHs,compared with that of the infinite case,is reduced by about 2.6%,20.7%,and 69.2%,respectively. The results of the single-layer materials are entirely lower than the corresponding values of 30.9%,56.6%,and 82.4%for WSe2,5.6%,35.5%,and 82.6%,respectively.

There is no denying that generally classical phonon size effects,which are employed to understand phonon MFPs with the characteristics length,were being significantly discovered in the microscale and nanoscale system.[57]If the size of the device refers to as small as the phonon MFP, the cumulative κ should considerably reduce due to the frequent phononsurface scattering. Therefore, the knowledge of MFP holds indispensable to focus on the size effects and is another key to understanding the phonon transport properties of nanocrystals,we also match the result to a single parametric function[31]

where κ0and lmaxrepresent the ultimate cumulative lattice thermal conductivity and the maximum MFP involved. l0is an assessment parameter to compute.

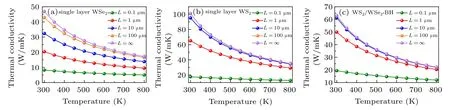
Fig.6. The lattice thermal conductivity variation of single-layer WSe2(a),WS2(b),and the WS2/WSe2-BHs(c)as function of temperature for different sample lengths(here infinite length sample,L=∞,refers to the case without phonon-boundary scattering).

These matched phonon dispersion curves included as mapped with dot lines in Fig.7, reproduce together the slope and the location of the computed result reasonably well. The cumulative κ of the WS2/WSe2-BHs, 2D WS2, and WSe2keep increasing as MFP increases, up to until reaching the thermodynamic limit. It yields the parameter l0of 233 nm,526 nm,and 1720 nm that can analyze and understand the illustrative MFP of the WS2/WSe2-BHs, 2D WS2, and WSe2,respectively. Compared to the l0of 526 nm and 1720 nm for 2D WS2and WSe2,the WS2/WSe2-BHs shows fundamentally smaller l0values. As a result,the size dependence of the value of κ for the WS2/WSe2-BHs is not so significant. Meanwhile,the phonon MFPs which contribute most to the total κ of the WS2/WSe2-BHs,2D WS2,and 2D WSe2are in the ranges of 60-600 nm,100-2000 nm,and 100-40000 nm,respectively.

Fig.7. Cumulative κ of the WS2/WSe2-BHs, 2D WS2, and 2D WSe2 versus the maximum phonon MFP at RT.The dot lines are drawn with curves,matching the above single parametric function.

3.3. Phonon group velocities and lifetimes

To analyze the thermal transport mechanism of heterostructure,the phonon group velocities and phonon lifetimes of the three models and different phonon branches in the heterostructure are compared in Fig.8. Phonon group velocities can be obtained directly by the slope of the phonon modes.Below,we have computed the group velocities of the phonon modes ωsby the slope of the phonon modes, which can be given by[58,59]

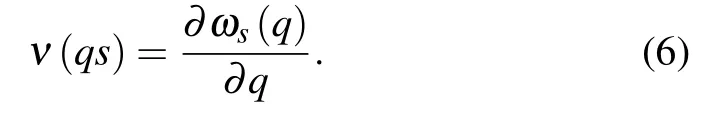
On the other side,we also calculated the phonon lifetimes by the phonon linewidth 2Γqs(ω)of the phonon modes[58,60]

where Γqs(ω) is a form analogous to the Fermi’s golden rule and completely incorporates scatterings from the entire phonon modes.[61]

From Fig.8(a), we can observe that most of the ν decrease with increasing frequency because of the unstiffened phonon modes. The ν of the acoustic and optical branches in the relatively low frequency region are those in the high frequency range. Thus, the low frequency acoustic and optical branches play a dominant role in phonon transport. More importantly, one interesting phenomenon is that the ν of the optical branches is even larger than those of acoustic branches which is rarely reported in the previous literature. Figure 8(b)displays that the frequency dependent group velocity of the WS2/WSe2-BHs is comparable with that of 2D WS2and WSe2. From Fig.8(b), it should be noted that the highest ν of the WS2/WSe2-BHs (5.18 km·s−1) is comparatively higher than that of the 2D WS2(4.75 km·s−1) and 2D WSe2(4.48 km·s−1) at relatively low frequency region. To compare the group velocity completely, the average values of the WS2/WSe2-BHs, 2D WS2, and WSe2are calculated and are 0.53 km·s−1,0.67 km·s−1,and 0.52 km·s−1,respectively. The phonon lifetimes considering all kinds of scattering processes,including boundary scattering,defect scattering,and phononphonon Umklapp scattering, are also compared in Fig.8(c).In Fig.8(c),it is worthwhile mentioning that the distributions of τ at low frequency acoustic and optical modes(lower than 4 THz) are frequency-independent. Figure 8(d) displays the frequency dependence of τ of the three models.It can be found that the τ of the WS2/WSe2-BHs are distributed between those of 2D WS2and WSe2, especially in the relatively high frequency range(greater than 8 THz). The variation trend of the τ is consistent with the κlatof the WS2/WSe2-BHs,2D WS2,and WSe2. Combining the results presented in Figs.2,3,and 8, we conclude that the vdW interfacial interaction leads to a change in the Debye temperature and weakens the group velocities of phonon branches of the WS2/WSe2-BHs. These results can result in the reduction of the κlataccording to the Slack’s theory.[62]

Fig.8.Frequency versus(a)phonon group velocities(ν)and(c)phonon lifetimes(τ)of the whole phonon branches at RT for WS2/WSe2-BHs.Frequency versus(b)ν and(d)τ at RT for WS2/WSe2-BHs,2D WS2,and 2D WSe2.

To further understand the intrinsic physical mechanism of phonon transport and clarify the differences between the three materials,we have calculated the three-phonon scattering process and the Gr¨uneisen parameter. Aimed at the three-phonon scattering process, it is significant to understand how a multitude of scattering channels are available for phonons to be scattered. For further insight into the τ,the three-phonon scattering phase space (P3), which can qualitatively describe the three-phonon scattering process including the N and U processes,is calculated using the following equation[61]and plotted in Fig.9:

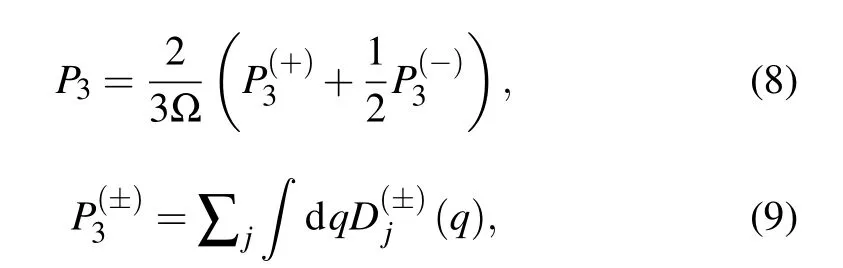
Fig.9. Comparison of the P3 phase space with respect to frequency for the WS2/WSe2-BHs,2D WS2,and WSe2.

3.4. Gr¨uneisen parameters

The Gr¨uneisen parameter γ, which provides the anharmonicity information of models, is suitable to analyze and understand the thermal transport properties of nanomaterials.The expression of γ can be written as[63]

where α represents the linear thermal expansion coefficient,Vmand B represent the molar volume and the bulk modulus,respectively, and CVrefers to the phonon volumetric specific heat. The mode γ is described as[44]

where ωs(q) represents the frequency of the s-th phonon mode, and a0represents the equilibrium lattice parameter at 0 K.

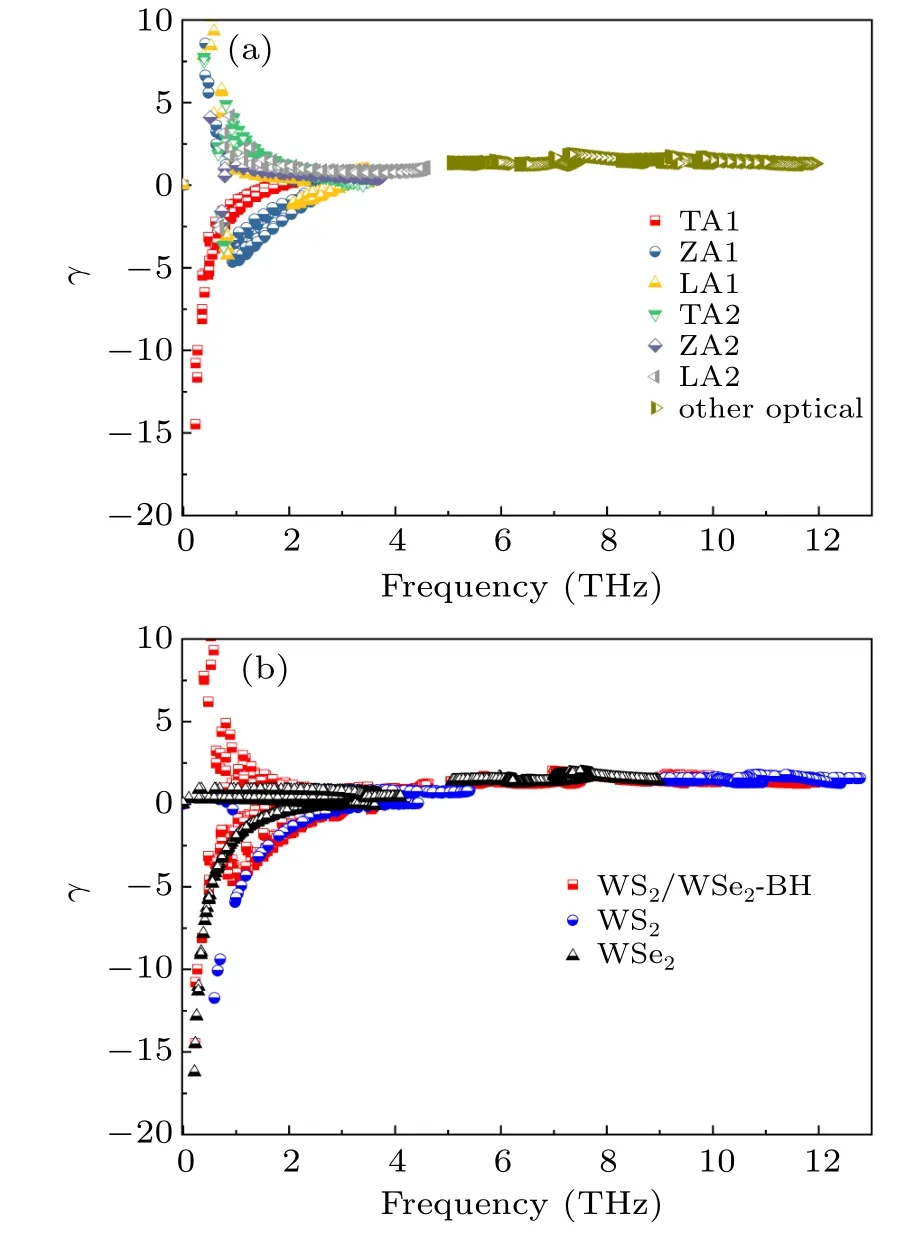
Fig.10. (a)Calculated γ parameters versus the frequency of the whole phonon branches for WS2/WSe2-BHs. (b) Calculated γ parameters virus the frequency for WS2/WSe2-BHs,2D WS2,and WSe2.

The calculated γ of WS2/WSe2-BHs are depicted in Fig.10(a). The γ of ZA1located at the relatively low frequency region displays a large positive and fractional negative, which is consistent with 2D WS2and WSe2.[64]It has previously been observed and focused on the other 2D structures such as graphene, and is mainly caused by the influence of membrane.[65]The large value of |γ| for the phonon modes usually demonstrates strong anharmonicity which gives rise to the low value of klat. Obviously, the value of |γ| of TA1reaches to 15 at the Γ point, indicating that the phonon mode expresses strong phonon-phonon anharmonicity. Furthermore, in Fig.10(a), large |γ| almost exists in the relatively low frequency region(＜4.73 THz),which significantly contributes to the anharmonic effect for the WS2/WSe2-BHs.Generally,for the materials,including lone-pair electrons,the non-bonded electrons influenced with the valence electrons of the neighboring atoms,would lead to increased anharmonicity at controlled temperature.[66]From Fig.10(b), the γ of high frequency optical modes nearly keep as a constant, which indicates that the contribution of the optical modes to the anharmonic effect is very little. Moreover, we have also found that the WS2/WSe2-BHs possesses a smaller γ comparing with 2D WSe2, which will lead to a larger κlatof the heterostructure.

3.5. Charge density distribution

As mentioned above, the atomic vibrations perpendicular to the xy plane are affected by the vdW interaction. For the modification on the elastic modulus of nanostructure resulted from the interface charges,[67]the interface effects usually play a significant role in exploring phonon and thermal transport properties of the vdW heterostructures. Therefore,the distribution of charge density difference of the WS2/WSe2-BHs and the charge redistribution and transfer among the single-layer WS2and WSe2surfaces can be gained as shown in Fig.11. The charge density difference(Δρ)can be obtained by

Fig.11. (a) The top- and side-views of charge transfer across the interface of the WS2/WSe2-BHs. (b) The average plane charge density difference Δρavg(Z) along the Z direction for the WS2/WSe2-BHs. The gray, yellow,and green spheres indicate W,S,and Se atoms,respectively.

The data of the charge transfer (gaining and losing electron)among the atoms can be obtained from the charge density difference. In Fig.11,we can notice that the charge decreases mostly at the Se atoms,in addition it increases at the S atoms,making electron-hole pairs dispersed for the WS2/WSe2-BHs interface. To estimate the charge transfer, the plane-averaged charge density difference Δρ(Z)avgalong the Z direction is plotted in Fig.11(b). There are many reasons for the charge transfer,having a weak orbital overlap among the heterostructures,the polarization and potential gradient fields of adjacent layers.[68]From Fig.11(b), it can be noticed that the transferred interlayer charge density can reach to (～0.06 e/Bohr)due to the existence of vdW,which can significantly improve the anharmonic scattering among propagating phonons along the plane direction and consequently diminish the κlat. It is well known that three factors, including the interfacial interaction, charge redistribution, and electron-hole pair separation, are generally supplemented by an improvement in optical transitions in the vdW heterostructures.[69]Based on the above analysis, we can understand the change of κlatof the WS2/WSe2-BHs from the perspective of charge transfer.

4. Conclusion

The phonon transport properties of the WS2/WSe2-BHs were systematically studied by the linearized phonon BTE combined with the conventional first principles method.We found that the κlatof the WS2/WSe2-BHs was about 62.98 W/mK at room temperature. The result demonstrates that the three-phonon scattering plays an important role in phonon transport, and that the three acoustic modes are the main heat carriers. We compared the average κlatvalue(74.27 W/mK) of WS2and WSe2single-layers with that of the WS2/WSe2-BHs, and found that the interlayer coupling and the kinks in acoustic branches result in the variation of the κlat. Additionally, we obtained a parameter l0of 233 nm for the WS2/WSe2-BHs, and it is critical to thermal management with nanostructured crystals. Lattice thermal conductivity can be effectively modulated when the nanostructure scope is below the representative phonon MFP. The purpose of this work aims at understanding the mechanism of phonon transport in vertically stacking TMDCs heterostructures and further promoting their thermal management applications in optoelectronics and thermoelectric materials.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.