Soliton interactions and asymptotic state analysis in a discrete nonlocal nonlinear self-dual network equation of reverse-space type∗

Cui-Lian Yuan(袁翠连) and Xiao-Yong Wen(闻小永)

School of Applied Science,Beijing Information Science and Technology University,Beijing 100192,China

Keywords: reverse-space nonlocal nonlinear self-dual network equation, nonlocal discrete generalized(m,N −m)-fold Darboux transformation,multi-soliton solutions,rational solutions

1. Introduction

Nonlinear lattice equations (NLEs) can be regarded as spatially discrete analog of nonlinear partial differential equations. As the models of some physical phenomena, NLEs have received widespread attention and may be used to describe many certain physical situations such as nonlinear optics, nonlinear lattice dynamics, ladder-type electric circuits,feader-eater process in biology, Langmuir waves in plasma physics (see Refs. [1-7] and references therein). For example,Wadati[1]proposed a ladder-type nonlinear LC circuit diagram,which can be governed by the NLE as follows:

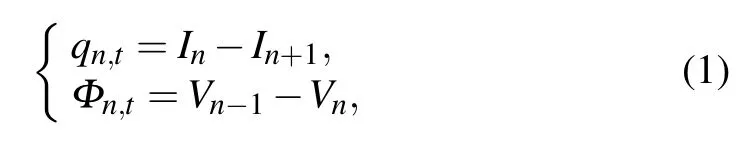
where qn=C(Vn)Vnand Φn=L(In)Inrepresent the electric charge in the n-th capacitance and magnetic flux across n-th inductance, respectively. The voltage dependent capacitance C(Vn)and the current dependent inductance L(In)can result in nonlinearities of Eq.(1). When taking C(Vn)=arctan(Vn)/Vnand L(In)=arctan(In)/In,Eq.(1)reduces to the famous nonlinear self-dual network equation which was first introduced by Hirota to describe the propagation of electrical signals in a nonlinear, lumped, self-dual ladder-type electric circuit.[2]Since nonlinear self-dual network equation was proposed, it has attracted a great deal of attention due to its special physical background.[1,3,8-14]In Ref.[8],Ablowitz and Ladik proposed a coupled discrete nonlinear integrable equation with four potentials:

In 2013,Ablowitz and Musslimani first proposed the continuous PT-symmetry nonlocal nonlinear Schr¨odinger(NNLS)equation from a new symmetry reduction of the well-known AKNS system, which is an integrable system admitting the Lax pair and an infinite number of conservation laws,and has been solved by the inverse scattering transform method.[15]The PT-symmetric NNLS equation, which can keep lossless propagation due to the balanced gain and loss,[16]admits remarkable new characteristics that are not observed by comparison with its classical standard NLS equation and has received great attention,see Refs.[15-21]. Moreover,in Refs.[22,23],Ablowitz and Musslimani proposed many different nonlocal counterparts of known continuous and discrete nonlinear integrable equations. Subsequently, many other nonlocal nonlinear integrable equations have also been proposed and studied,such as the nonlocal modified Korteweg-de Vries equation,[24](2+1)-dimensional nonlocal NLS equation,[25]nonlocal Manakov system,[26]nonlocal Burgers equation,[27]nonlocal twowave interaction system,[28]nonlocal short pulse equation,[29]nonlocal Gross-pitaevskii equation,[30,31]PT-symmetric coupled NNLS equations.[32]Like their local versions, nonlocal integrable systems admit Lax pair, conservation laws, soliton solutions and some integrable properties,[15,17]and they also admit certain new features and cannot be realized in contrast with their local counterparts that further make the subject attractive. However,it is easy to find that most research results of nonlocal equations are the study of continuous nonlocal integrable equations, while the revelent research of discrete NLEs is not sufficient.[9,33-37]Especially, the study of nonlocal discrete equations is not systematic,[38-41]so focusing on discrete nonlocal NLEs motivates us.

In this paper, inspired by the idea of Ablowitz and Musslimani in Refs.[15,22,23]and based on the previous work in Refs.[9,10],for Eq.(6),if we take a simple reduction Rn=In,Sn=Vn, Qn=σI−n, Tn=σV−nand h=g=1, then Eq. (6)can reduce to the following new discrete reverse-space nonlocal NLE:

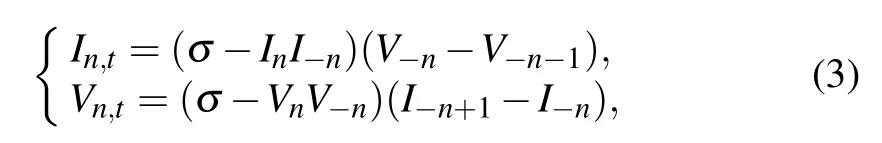
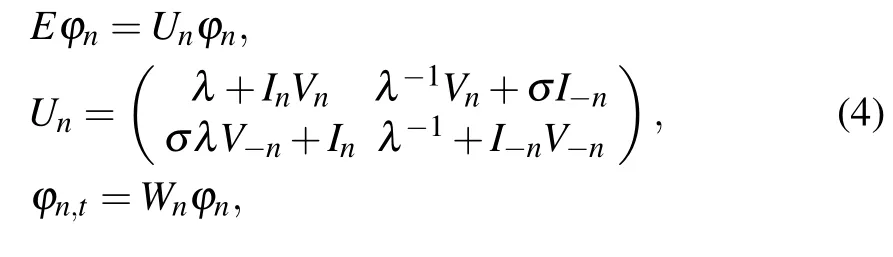
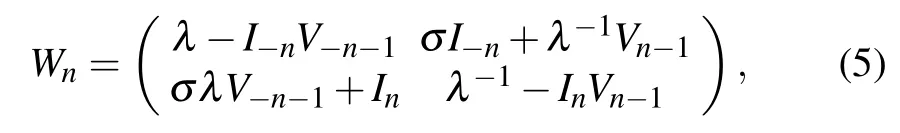
where ϕn=(φ1,n,ψ1,n)T, λ means the spectral parameter independent of time t, and in this nonlocal system we define the shift operator E by E f(±n,t) = f(±n+1,t) =f±n+1,E−1f(±n,t) = f(±n −1,t) = f±n−1. The compatibility condition Un,t= (EWn)Un−UnWnbetween Lax pair(4) and (5) just leads to Eq. (3), which is PT-symmetric for the reason that the potential terms G(n,t)=σI(n,t)I(−n,t)and H(n,t) = σV(n,t)V(−n,t) obey the PT-symmetry, i.e.,G(n,t)=G(−n,t), H(n,t)=H(−n,t). PT-symmetry invariance is particular because the local solution state at location n is directly coupled to the nonlocal solution at remote location−n,which is very similar to quantum entanglement between a pair of particles.[29]Due to the physical background of nonlinear self-dual network equation, physicists and engineers may design a PT-symmetry nonlocal electronic circuit diagram by utilizing Eq.(3),so Eq.(3)may possess potential application value in electric circuits.

Some methods for solving local equations have been extended to nonlocal equations such as the inverse scattering transform method,[15,24,30]Hirota’s bilinear method,[25,26,31,32,42-44]the function expansion method,[27]the Riemann-Hilbert method,[28]and the DT method.[9,12,16,29,33,35-41,45-51]Among them, DT is a simple algebraic technique to generate a family of infinite nontrivial solutions of a linear equation from a known trivial solution which is widely used in soliton theory.[9,45,46]It needs to be noted that the N-fold DT technique is a very effective method to derive N-soliton solutions compared to iterative DT because there is no iterative process. Recently, a generalized(m,N −m)-fold DT method, taken as a generalization of the N-fold DT,was proposed by one of the authors of this paper,and it not only expresses soliton solutions but also gives some rational solutions and mixed interaction solutions of rational solutions and usual soliton solutions.This technique was originally used in continuous local models, and then gradually extended to continuous nonlocal models,discrete models and discrete nonlocal models. However, for the discrete nonlocal NLEs,the relevant research and theory are still not systematic and sufficient,so it is a meaningful research work to continue to develop and improve this technique. To the best of our knowledge, the discrete nonlocal multi-soliton solutions and relevant dynamical behaviors of the new reverse-space nonlocal Eq.(3)have not been reported yet in literature. Therefore,in this paper,we further investigate Eq.(3)via the generalized(m,N −m)-fold DT technique.

In addition, before discussing Eq. (3), according to Ref. [10], we also propose a new high-order reverse-space nonlocal nonlinear self-dual network equation

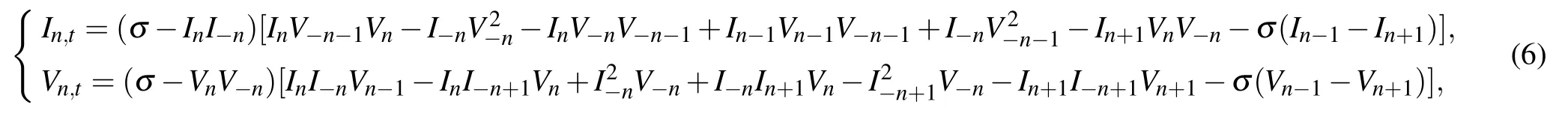
and we here give its new lax pair different form one in Ref. [10], the space part of Lax pair for Eq. (6) is same as Eq. (3) (i.e., Eq. (4)), while the time part of its Lax pair is given in the following form:

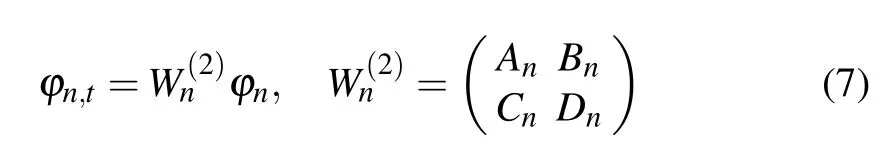
with

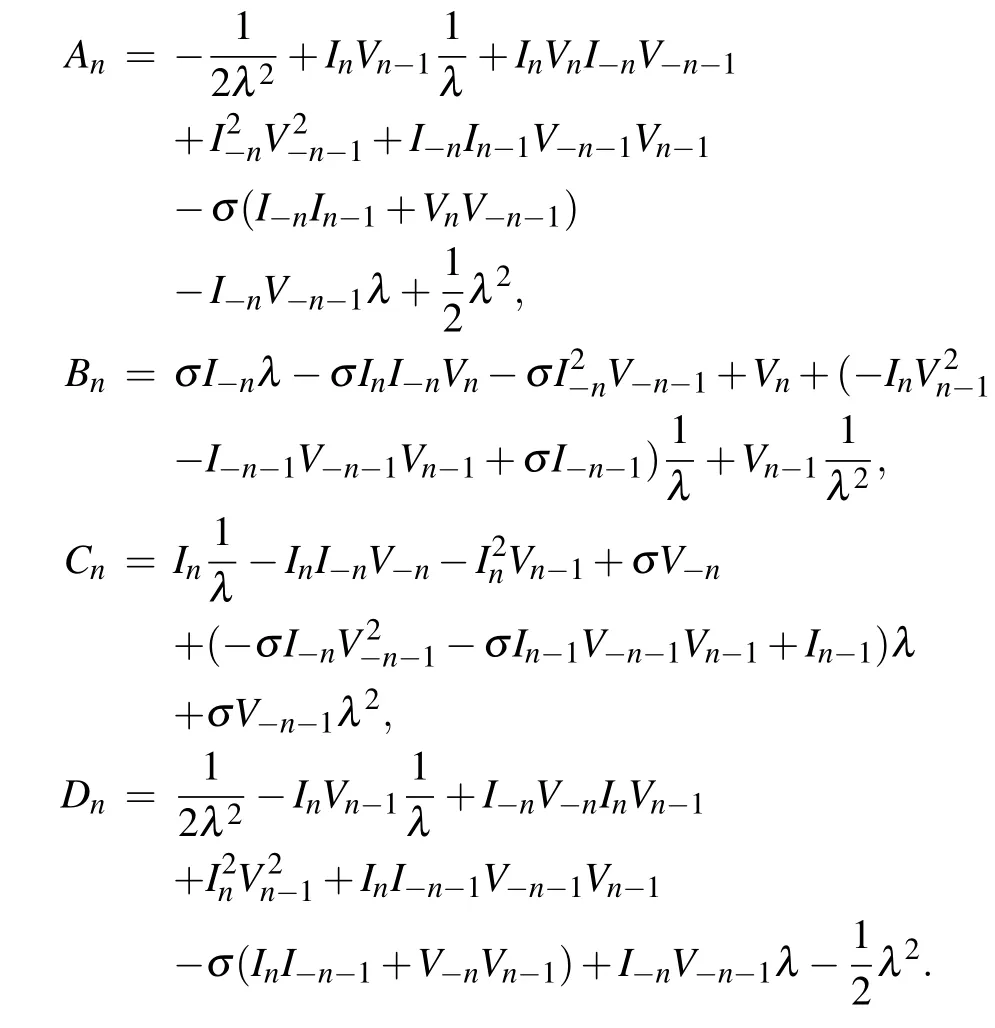
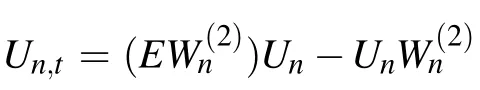
The rest contents of this paper are the followings. In Section 2, we construct nonlocal infinitely many conservation laws of Eq. (3). In Section 3, the nonlocal version of(m,N −m)-fold DT for Eq.(3)is constructed based on its Lax representation. As applications, the discrete nonlocal multisoliton solutions and rational solutions are calculated via the nonlocal discrete N-fold DT technique (discrete generalized(m,N −m)-fold DT with m=N)from vanishing background and the nonlocal discrete(1,N −1)-fold DT(discrete generalized(m,N −m)-fold DT with m=1)from nonzero seed background,respectively. Moreover,the soliton propagation properties and asymptotic state analysis are analyzed and discussed graphically, and a few wave features of rational solutions are summed up as well. Last section will be devoted to some conclusions.

2. Conservation laws of Eq.(3)

Conservation laws are important to justify the integrability for integrable system.[1,52]In this section, we shall derive the infinitely many conservation laws for Eq. (3). Firstly, we can get from Eqs.(4)and(5),

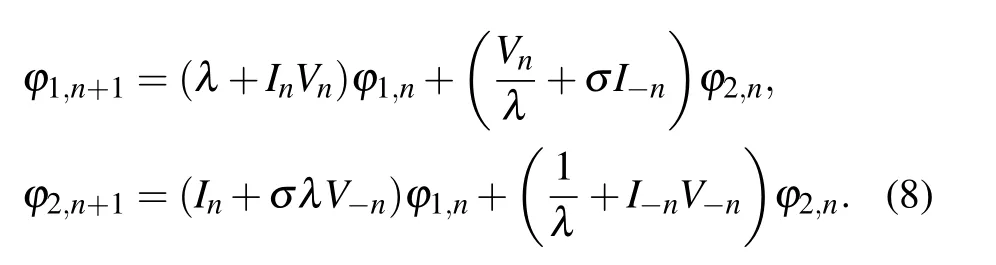
Setting θn=ϕ2,n/ϕ1,n,we obtain

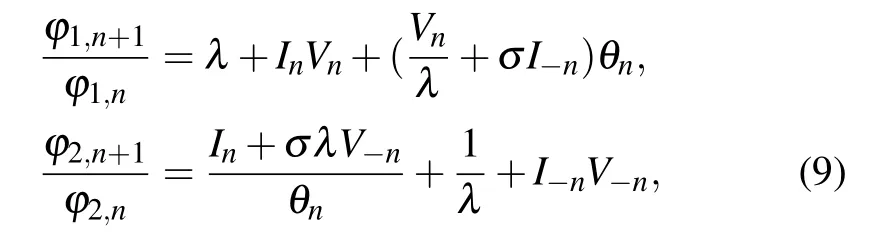
from which we have

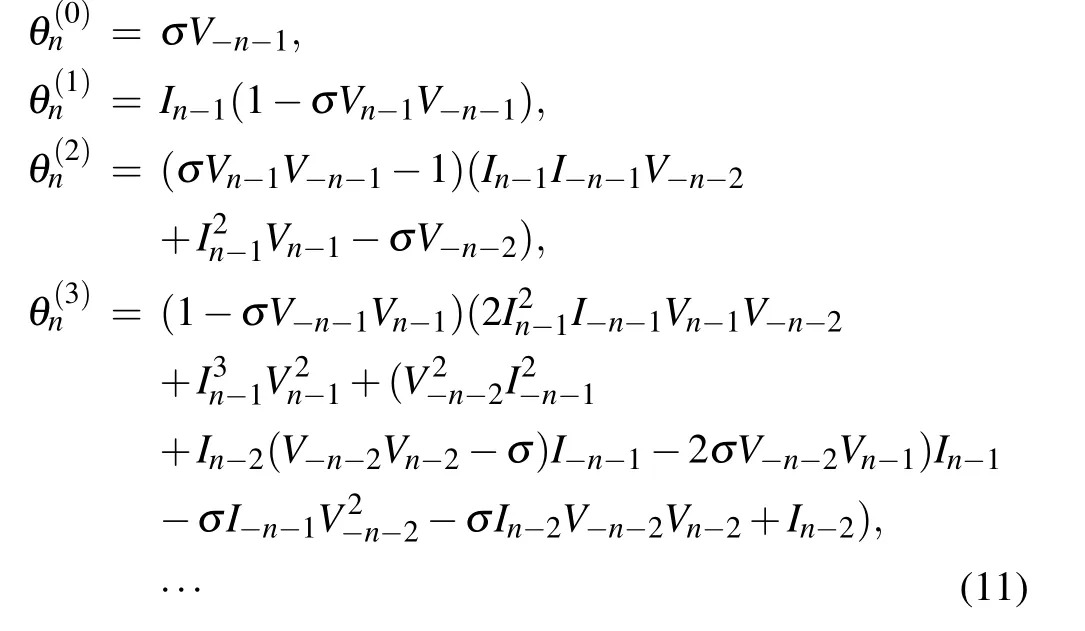
By means of Eqs.(5)and(9),we have

Taking Eq. (11) into Eq. (12) and equating the same powers of λ in Eq. (12) generate an infinite number of conservation laws to Eq. (3), and the first two conservation laws are listed as follows:

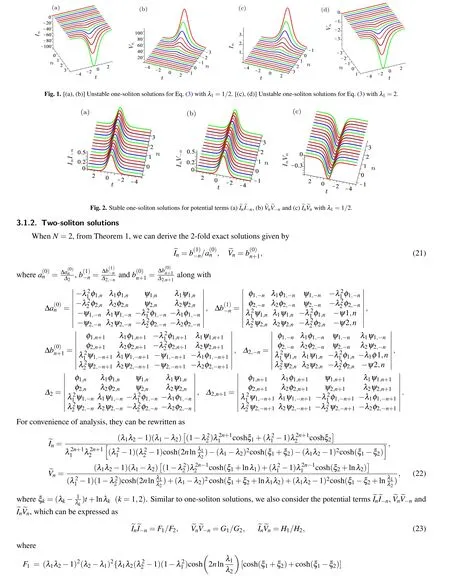
4. Conclusion

In summary,we have analytically investigated a reversespace nonlinear self-dual network equation(3)with σ =−1,which may describe the propagation of electrical signals in a ladder-type nonlinear self-dual network. We summarize the main achievements of this paper as follows: (1) An infinite number of nonlocal conservation laws for Eq. (3) have been constructed. (2)The discrete nonlocal version of generalized(m,N −m)-fold DT is extended to nonlocal Eq.(3)in detail for the first time, which is a generalization of the usual discrete N-fold DT. (3) The asymptotic state analysis for two-soliton solutions are investigated, and the related properties of wave propagation are shown and discussed in detail. (4)It is found that individual components in this nonlocal equation(3)possess unstable soliton structures while the potential terms have the stable soliton structures,which also shows that the energy of this equation is conserved from another aspect. (5)Mathematical features of different-order rational solutions of Eq.(3)are summarized,from which we can see that the nonzero backgrounds for rational solutions appear alternately between two components in this system.

In theory, it is entirely possible to expand eigenfunctions at more spectral parameters to get more new solutions to Eq.(3)via the discrete generalized(m,N −m)-fold DT.However, in fact, the calculations are very complicated, we need further investigation in this field. We think that the key idea of this technique can be applied to other discrete local and nonlocal nonlinear integrable models as well. Finally, we need to point out that Eqs. (3) and (6) provide the possibility for designing nonlocal electrical circuits, and the results of this paper also provide a theoretical basis for enhancing and weakening the propagation of electrical signals in electrical circuits.We hope that the results obtained in this paper may be useful for explaining the electrical signals’ propagation phenomena in practical applications.

Acknowledgment

We would like to express our sincere thanks to other members of our discussion group for their valuable comments.