Investigating the thermal conductivity of materials by analyzing the temperature distribution in diamond anvils cell under high pressure

Caihong Jia(贾彩红) Min Cao(曹敏) Tingting Ji(冀婷婷) Dawei Jiang(蒋大伟) and Chunxiao Gao(高春晓)

1State Key Laboratory of Superhard Materials,Jilin University,Changchun 130000,China

2College of Mathematics and Physics,Inner Mongolia University for Nationalities,Tongliao 028043,China

Keywords: thermal conductivity,heat radiation effect,temperature field,diamond anvil cell

1. Introduction

Currently,the diamond anvil cell(DAC)is the only static high-pressure device that can generate an environment with a pressure as high as 1 million atmospheres.[1-3]In combination with electrical, optical, magnetic, mechanical and other methods to measure physical properties, a DAC can characterize material structure and various physical properties under high pressure.[4-8]Accordingly, DACs have been widely applied in diverse fields including materials science,physics and chemistry.[9-14]When a DAC is subjected to high temperatures it can simulate the conditions in the earth’s interior in the laboratory, which is of great importance for investigating the thermal properties of minerals and rocks.[15-17]However,it is an enormous challenge to characterize the thermophysical properties of the material under test at conditions of extremely high temperature and high pressure (HT-HP).[18]This challenge is even more pronounced in the DAC platform.

Currently, the thermal transport properties of materials in a DAC are mostly studied through the laser flash method.[19-23]However,this method has some disadvantages,such as the technological challenges involved in preparing samples. In order to accurately measure the heat transport properties of materials under extreme conditions,innovations have been proposed to measure the steady-state heat conductivity of materials through a DAC.[17]The main idea in this regard was to realize the temperature gradient of samples by directly heating the upper and lower diamond anvils(DAs)in a high-temperature resistant furnace. Therefore, it is essential to calculate the temperature distributions in the sample to study thein situheat transport properties in the DAC.To this end, replace contact temperature measurement is often used in the steady-state method. It is worth noting that because of the high thermal conductivity of diamond it can be regarded as a thermostatic substance. Accordingly, the temperature of the diamond side edge measured by the thermocouple can be used as the temperature of the sample surface. Despite the remarkable advantages of this method,it cannot directly measure the temperature of the sample surface. Meanwhile, further investigations into the reliability of the replace contact temperature measurement method should be carried out when a temperature gradient exists in the anvil itself. In this regard,Yueet al.showed that conventional contact temperature measurement inevitably produces experimental errors that cannot be ignored. Accordingly, they combined the finite element method with multi-thermocouple local temperature measurement and analyzed the temperature distribution in the anvil and sample.[17]Accordingly,it was found that the outer wall of the DAC radiates heat to the surrounding flow through surface radiation, and the heat loss caused by surface radiation significantly affects the temperature field distribution in the DAC.Diamond can be considered a translucent medium. Since heat rays can penetrate deep into the material, the transmission of a semitransparent medium is different from that of most solid materials.[24]Based on this hypothesis, there is not only heat conduction in the anvil but also heat absorption, re-emittance and energy scattering within the anvil volume.[25]Therefore,heat transfer is quite a complex phenomenon in a DAC under stable heating conditions. A review of the literature indicates that the influence of radiant heat on the temperature field of the main components of a DAC is usually neglected.

In the present study, we aim to realize the temperature gradient distribution of the sample by directly heating the upper and lower bases of DAs in a high-temperature resistant furnace. In order to accurately measure thein situthermal conductivity of the sample in the DAC under HT-HP conditions, a radiative-conductive coupled heat transfer model is proposed to analyze the heat transfer in key components of the DAC under stable heating conditions. It is worth noting that the influence of the radiation effect on the temperature distribution of the DAC can be simulated through numerical methods. The main purpose of the present study is to investigate the feasibility of thermal conductivity measurement by combining numerical simulation and local temperature measurement of thermocouples in DAs at high pressures. This study is expected to provide a reference for the accurate measurement ofin situthermal conductivity in a DAC under HT-HP conditions.

2. Numerical method

The geometric structure of the diamond anvils,gasket and sample (DAGS) was modeled in accordance with the experiment. Figure 1 illustrates the prepared model. In the experiment,type Ia diamond was used as the anvil.In order to realize the temperature gradient distribution of samples in the DAC,the anvil was fixed on a high-temperature seat. Considering the high thermal conductivity of diamond,the base of the anvil can be regarded as an isothermal surface.In this regard,T1andT2denote the temperatures of the upper and lower anvil bases,respectively. Moreover,T3andT4are the temperatures at the midpoint of the lateral edges of the upper and lower diamond anvilsD3andD4, respectively.T1-T4reflect the measured temperatures from four thermocouples.

In the present study, the DAC device is equipped with a vacuum facility to ensure a vacuum degree of 1 Pa around the DAC. A vacuum environment effectively eliminates air conduction and convection. On the other hand,thermal radiation efficiency is highest in a vacuum environment.[26]Therefore,it is necessary to consider the influence of the radiation effect on the temperature distribution in the DAC.Meanwhile,heat energy transfers from the upper and lower translucent anvil bases to the sample in the pressure chamber through conduction and radiation mechanisms.

Fig. 1. Schematic configuration of the diamond anvils, gasket and sample.T1-T4 are the measured temperatures from four thermocouples.

In the present study,a coupled radiative-conductive heat transfer model was developed based on the finite volume method(FVM)to simulate the temperature and heat flow field distributions in the DAGS.The proposed model fully considers the effects of radiation heat transfer in the diamond on the temperature distribution. Since the thermal radiation is highly localized, the sensitivity of angular discretization should be considered in the calculations. The heat flux of the wall results in non-physical oscillation in large discretization dispersion in the angular coordinate. As the angular discretization increases, the heat flow gradually becomes smooth. In this scheme,thein situthermal conductivity of the sample is studied by combining numerical analysis and the locally measured temperatures via thermocouples in the DAC. In this regard,four thermocouples were arranged at the middle point of the side edge and the base of the upper and lower DAs.

In the calculations, the temperature boundary conditions of the upper and lower bases of the DAs are assumed to beT1andT2, respectively. Under a certain temperature boundary,the coupled radiative-conductive heat transfer model is used to simulate the temperature gradient of the sample in the DAC under HT-HP conditions.In all calculations,it is assumed that the thermal conductivity of the sample changes until the calculated temperaturest＇3andt＇4at the midpointsD3,D4of the lateral edges of the DAs reach the measured temperaturesT3andT4. In our previous study,a combination of temperature measurement through thermocouples and numerical analysis was realized to calculate the thermal conductivity of the sample in the DAC in the absence of radiation heat transfer.[17]Then this method was verified via the characterization of the thermal conductivity of diamond.[28]It was found that,as the diamond temperature increases, the influence of the radiation on the temperature field of the DAC increases. Since the radiationconduction heat transfer model is applied to analyze the heat fluxes, it is necessary to know the radiant characteristics of a Iatype diamond anvil. Tables 1 and 2 present the heat radiation characteristics and thermodynamic parameters of the DAGS used in the analysis.

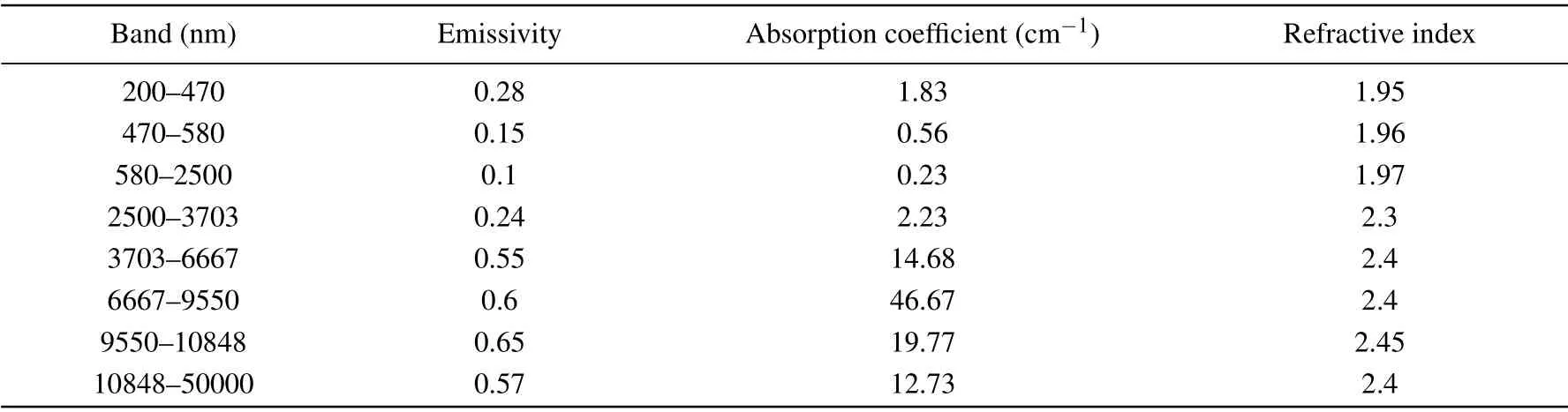
Table 1. Radiant characteristics of Ia-type diamond.

Table 2. Thermodynamic parameters of materials used in numerical simulation.

3. Result and discussion

In order to accurately measure thein situthermal conductivity in the DAC under HT-HP conditions, a radiationconduction coupling model was developed to study the influence of the radiation effect on the heat flow field of the DAC.When the mode of heat transfer in the DAC had been determined, the thermal conductivity of different materials under high pressure was studied with locally installed thermocouples at the boundaries.

3.1. Influence of the radiative effect on the heat transfer of the DAC

The DAC device was equipped with a vacuum housing to prevent convection of heat from the surrounding air. However,heat radiation intensifies in a vacuum environment. In order to evaluate the radiation effect on the temperature distribution in the DAC, the radiation-conduction coupling heat transfer model was used to quantitatively analyze the influence of radiation on the temperature and heat flow of the DAGS. The radiation consists of two parts,including the radiant heat loss on the outer wall of the DAC in the vacuum environment and the transmission and absorption of radiation inside the solid region of the DAs.

The presence of heat radiation leads to heat loss in the DAC, thereby decreasing the overall temperature. In all simulations,T1andT2of the DA bases and the sample conductivity were set to 873 K, 943 K, and 2 W·m-1·K-1, respectively. Based on the radiation-conduction coupling heat transfer model, the heat transfer mechanism in the anvil and sample is confined to the radiation effect. Figure 2(a) indicates that the temperature and heat flow of the sample reduce to 2.38 K-2.60 K and 82 W·m-2-14785 W·m-2, respectively.Moreover, figure 2(b) reveals that the temperature decreases on the upper and lower walls of the sample. Figure 2(b) indicates that the temperature of the upper wall of the sample and the heat flux difference decrease to 2.44 K-2.59 K,and 6940 W·m-2-8520 W·m-2, respectively. Furthermore,the temperature of the lower wall and the heat flux decrease to 2.38 K-2.51 K and 90 W·m-2-1110 W·m-2, respectively.Figure 2(e) shows that the temperature of DAs along the lateral edges and the heat flux decrease to 0.3 K-3.06 K and 25276 W·m-2-34251 W·m-2, respectively. Accordingly, it is found that radiation is the dominant heat transfer mechanism in the entire flow field and affects the axial (longitudinal)temperature gradient. Studies show that thermal radiation dominates in the heat transfer process for materials with an extinction coefficient less than 20 cm-1at temperatures higher than 600 K.[30]Accordingly, the proportion of radiation heat transfer to total heat transfer increases as the temperatures of the bases of DAsT1andT2increase. It is observed that ignoring the radiant heat transfer leads to a large error in the DAC under HT-HP conditions. The proposed radiation-conduction coupling model is closer to the actual heat transfer in the DAC,which sufficiently considers the influence of heat radiation on the accuratein situmeasurement of the thermal conductivity of materials.

3.2. Measurement of thermal conductivity by analyzing the temperature field in the DAC

In measuring the thermal conductivity of samples in the DAC at high pressures, the temperaturesT1andT2of the upper and lower anvil bases are applied in the finite volume simulation as temperature boundary conditions. The sample temperature gradient in the DAC is simulated by the radiationconduction coupling heat transfer model at HT-HP conditions.The obtained results reveal that for different thermal conductivities of the sample,the calculated temperaturest＇3andt＇4are consistent with the measured temperature from thermocouples at the midpoint positionsD3andD4of the DAs. The input thermal conductivity reflects the thermal conductivity of the sample under this pressure. In other words, the thermal conductivity of the sample affects the temperature distribution in the DAC. In the proposed model, the thermal conductivity of the sample was determined by detecting the temperature change of the midpoint positionsD3andD4of the side edges of the anvils.

Fig.2. The heat loss originating from the radiation effect. (a)Temperature and heat flux contours in the sample. (b)Temperature and heat flux distributions on the upper and lower walls of the sample.(c)Distribution of heat flux in DAs.(d)Temperature distributions in DAs.(e)Temperature heat flux profiles in DAs.

Due to the high thermal conductivity of diamond,[31]it is necessary to analyze the feedback sensitivity at the temperature measuring point when the thermal conductivity of the sample changes to illustrate the feasibility of measuring thermal conductivity for different materials by analyzing the temperature distribution in the DAC.

In order to study the temperature gradient of DAs under HT-HP conditions,two lateral lines at the edges were selected in the upper and lower DAs, as shown in Fig. 3(a). Then the temperature gradient of DAs for different samples with different thermal conductivities, including 2 W·m-1·K-1,20 W·m-1·K-1,30 W·m-1·K-1,and 60 W·m-1·K-1,and differentT1-T2temperatures, including 873 K-903 K, 873 K-923 K,and 873 K-943 K,were simulated. Figure 3(b)shows the temperature distribution at 600µm-1200µm along the lateral edges of the upper and lower anvils forT1-T2temperatures of 873 K-943 K and different thermal conductivities. When temperaturesT1-T2vary from 873 K-903 K to 873 K-943 K,and sample thermal conductivity is 2 W·m-1·K-1,the temperature gradient of the upper anvil varies from 1.8 K to 4.4 K,while the temperature gradient of the lower anvil varies from 8.1 K to 15.1 K. In this regard, figure 3(a) shows that as the temperature difference ΔT(ΔT=T2-T1)increases,the temperature gradient of the lateral edges of the DAs intensifies significantly. Moreover,figure 3(b)shows that for constantT1andT2temperatures in the bases of the upper and lower DAs,the temperature gradient of the lateral edges of the upper and lower DAs increases gradually with an increase in the thermal conductivity of the sample.

Fig.3.(a)Temperature distribution along the lateral edges of the DAs.(b)Temperature distribution along the lateral edges of the DAs at 600 µm-1200µm.

The midpoint positionsD3andD4of the lateral edges of the DAs are defined as the positions where the temperature measurements were performed. Figure 4 shows the temperature distributions at measuring pointsD3andD4when the temperatureT1is set to 873 K,whileT2is set to 903 K,923 K,and 943 K, respectively. When the sample thermal conductivity increases from 2 W·m-1·K-1to 60 W·m-1·K-1andT1andT2are constant, temperatureT3varies from 874.6 K to 875.6 K at the midpoint positionD3and temperatureT4varies from 938.6 K to 937.7 K at the midpoint positionD4. Figure 4 indicates that variation of thermal conductivity of the sample is reflected in the temperature feedback at the temperature measurement point. Moreover, as the temperaturesT1andT2increase, the sensitivity of temperature measurement at pointsD3andD4improves. Temperature variations at the measuring pointsD3andD4can also be observed in experiments in the form of variations of the thermal conductivity of the sample.

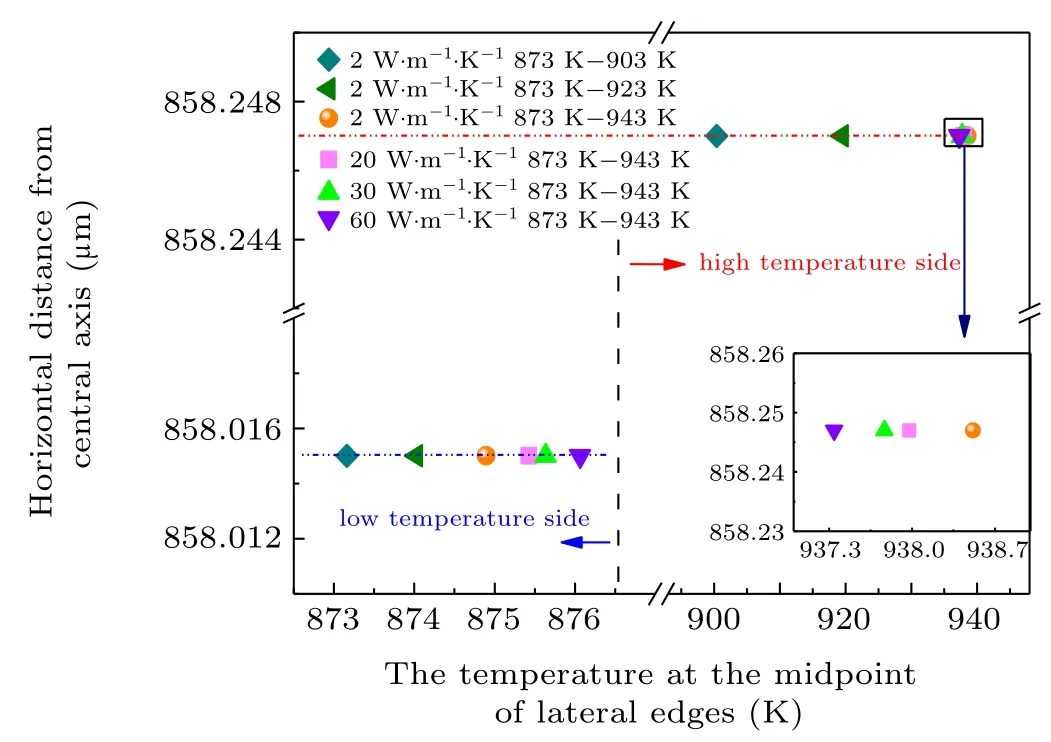
Fig. 4. Temperature distributions at the midpoint of the lateral edges of the DAs.

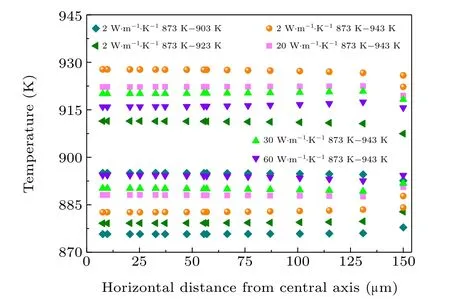
Fig.5. Temperature distribution at the sample walls.

In order to observe the temperature distribution of the upper and lower walls of the sample in the DAC, figure 5 shows the temperature difference at different sample wall positions in the DAC. The horizontal temperature gradient on the surface of the sample subjected to steady-state heating is small. When the thermal conductivity of the sample is 20 W·m-1·K-1,temperatures of the upper and lower surfaces of the sample are 922.2 K-919.4 K and 888.1 K-890.5 K,respectively. Moreover, when the thermal conductivity of the sample is 60 W·m-1·K-1, the temperatures of the upper and lower surfaces of the sample are 915.9 K-915.7 K and 894.3 K-894.4 K, respectively. Accordingly, it is found that when the sample thermal conductivity increases from 2 W·m-1·K-1to 60 W·m-1·K-1,the maximum relative temperature error of the two ends and the middle position of the same surface of the sample is less than 2.5%.We can conclude that as the thermal conductivity of the sample increases, this relative temperature error decreases and the temperature of the upper/lower wall can be set to a certain value.

Accurate measurement of thermal conductivity by analysis of the temperature distribution in a DAC under highpressure conditions has outstanding advantages. In this scheme,T1-T4are the measured temperatures from four thermocouples.The measured temperaturesT1andT2will be input to the FVM as boundary conditions. During the simulation,it was assumed that the thermal conductivity of the sample varies until the simulated temperaturest＇3andt＇4at theD3andD4reach the measured temperaturesT3andT4. Therefore,the input thermal conductivity reflects the real thermal conductivity of the sample. Figure S1 shows a flowchart for calculating the thermal conductivity of the sample in a DAC.

4. Conclusion

Studies show that the heat radiation effect has a great influence on the temperature distribution when the temperature gradient distribution of a DAC is realized by the steady-state method. In the present study, a coupled radiative-conductive heat transfer model is proposed to study the heat transport properties of samples in a DAC under HT-HP conditions. The main objective of this study was to avoid the influence of thermal radiation on thein situthermal conductivity of the samples. To this end, the feasibility of investigating the thermal conductivity of different materials by combining the proposed numerical model with locally measured temperatures by thermocouples is discussed. Based on the obtained results, it is found that variations in the thermal conductivity of the sample have obvious temperature feedback at the temperature measurement point in the DAC, which has a certain guiding significance in the experiment. Combining the coupled numerical model with locally measured temperatures is an effective technical approach for simulating the temperature field, thermal conductivity and other thermal transport properties of the sample in a DAC under extreme HT-HP conditions. This paper is expected to provide a foundation for accurate measurement ofin situthermal conductivity in DACs under HT-HP conditions.

Acknowledgments

Project supported by the National Key Research and Development Program of China (Grant No. 2018YFA0702700)and the National Natural Science Foundation of China(Grant Nos.11674404 and 11774126).