涡流发生器对风力机翼段动态失速影响
2021-03-19赵振宙孟令玉王同光苏德程吴昊许波峰
赵振宙, 孟令玉, 王同光, 苏德程, 吴昊, 许波峰
(1.河海大学 能源与电气学院,江苏 南京 211100;2.内蒙古工业大学 风能太阳能利用技术教育部重点实验室,内蒙古 呼和浩特 010000;3.南京航空航天大学 江苏省风力机设计高技术研究重点实验室,江苏 南京 210016)
涡流发生器是一种流动控制技术,能延迟气流分离,有效改善叶片气动特性[1-2]。文献[3]通过风洞试验发现:DU系列钝尾缘厚翼型翼段加涡流发生器后,其失速攻角发生延迟,最大升阻比增大。Zhang等[4]通过数值模拟指涡流发生器改变了上翼面边界层的压力梯度分布,揭示了涡流发生器的流动控制机理。涡流发生器对翼段静态失速的影响规律方面已经做了不少工作[5-8],这些研究提高了涡流发生器控制静态风力机叶片表面流动的机理认知水平。
在实际环境中,风机叶片不仅会因为雨蚀、沙蚀、蚊虫附积、结冰[9]等问题影响叶片表面流动,在偏航、变桨、剪切风等影响下,风力机叶片因攻角随时间连续变化还会产生动态失速现象[11]。与静态失速不同,动态失速下叶片表面的分离非常复杂,失速攻角远比静态失速攻角大,升阻力特性随攻角变化出现明显的迟滞现象[11-12]。根据失速特性不同,动态失速可分为轻失速与深失速[13],从航空翼型在正弦规律俯仰运动下动态失速研究结果看[14],轻失速一般发生在下俯阶段,表现为后缘分离,分离边界层厚度为翼型厚度量级;深失速通常发生在上仰阶段,前缘分离,分离边界层厚度达翼型弦长量级。与航空翼型不同,风力机专用翼型有其自身的气动特点,文献研究发现后者在深失速下也表现为后缘分离[15]。
有学者研究了涡流发生器对翼段正弦规律俯仰运动下动态失速过程的影响。如:文献[16-18]对OA209翼段前缘点附近加涡流发生器后的动态失速过程进行了试验研究,发现动态失速涡强度变小,载荷波动性得到了改善,但最大升力系数有所减小。然而,上述研究均以航空翼型段为对象,且涡流发生器均安装于前缘点附近。戴丽萍等[19]对20%弦长处加涡流发生器的风力机专用翼型DU97-W-300翼段的动态失速进行数值模拟,结果表明加涡流发生器后翼段气动性能得到明显提高。从现有文献总的来自看,针对加涡流发生器的风力机专用翼型翼段动态失速过程的研究很少,涡流发生器对其深失速和轻失速影响还有待进一步的研究。
本文采用延迟分离涡模拟(DDES)方法,对加涡流发生器的风力机专用翼型DU91-W2-250翼段深失速和轻失速进行数值模拟,旨在揭示涡流发生器对深失速和轻失速的影响规律。
1 数值模拟方法
1.1 模拟方法
分离涡模拟(detached-eddy simulation,DES)方法在近壁区使用RANS(Reynolds-averaged Navier-Stokes)方法,解决了LES(large eddy simulation)方法近壁面网格数量庞大的缺点,在远离壁面主流区采用可以更精细地捕捉涡结构的LES方法,文献[20]为解决DES方法的模型应力损失问题,提出了改良后的延迟分离涡模拟(delayed DES,DDES)方
法。本文中DDES方法在近壁区采用k-ωSST模型。由于篇幅原因,本文DDES方法的具体内容不再阐述,详见文献[21]。
1.2 几何模型和网格
DU91-W2-250为荷兰Delft大学设计的风力机专用翼型,其展长0.105 m、弦长c为0.6 m,最大厚度为25%c,位于距前缘点32.2%c处。本文在20%c处布置三组反向旋转排列的涡流发生器。涡流发生器为三角翼结构,弦长17 mm,高5 mm,攻角为16.4°,组间距35 mm,涡流发生器结构尺寸如图1所示。

图1 涡流发生器尺寸结构Fig.1 Configuration of VGs
模型计算域分为静止的圆形外域与运动的圆形内域,外域半径为20c,内域半径为3c,如图2(a)。翼面第1层网格满足条件Y+≈1,边界层处网格法向增长率为1.1。三角翼涡流发生器采用无厚度三角形面网格代替,若设三角形面网格为内部边界,几何模型转变为光滑翼段;若设三角形面网格为无滑移壁面条件,几何模型即为加涡流发生器的翼段。这可以保持光滑和加涡流发生器翼段的网格一致,计算结果更具对比性。翼段处网格结构如图2(b),采用六面体结构化网格,网格总数500万。
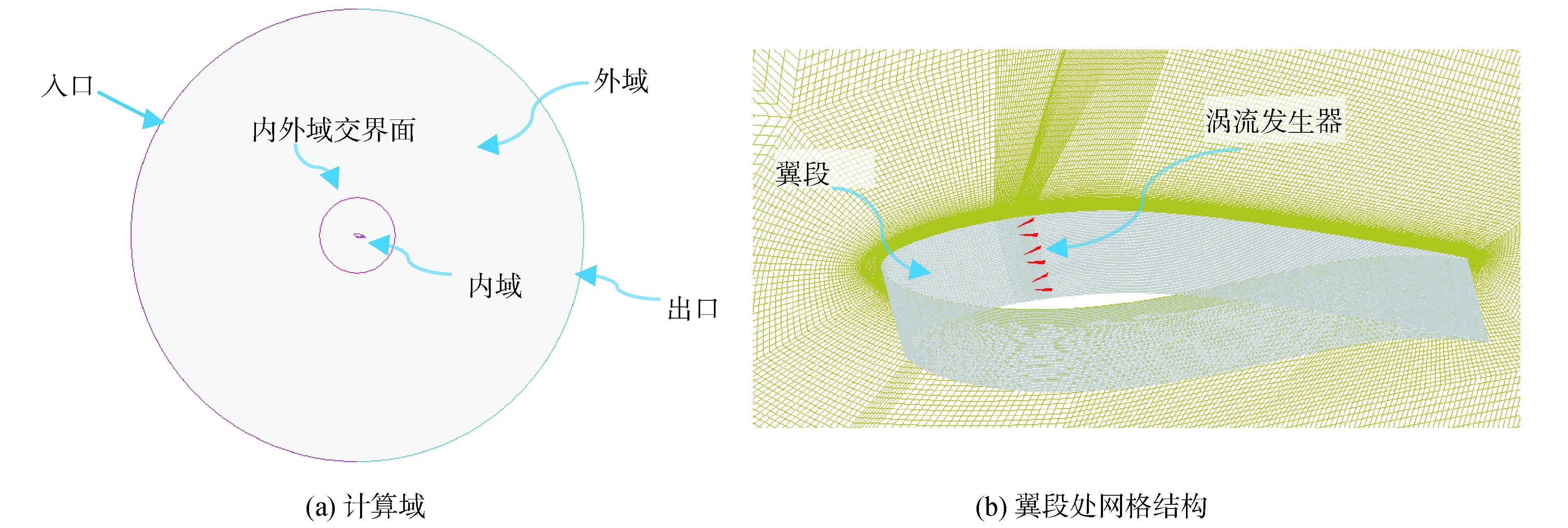
图2 计算模型Fig.2 Computational model
1.3 计算条件
雷诺数为2×106,空气密度ρ=1.225 kg/m3,动力粘度μ=1.789 4×10-5kg/(m·s)。采用速度入口边界条件,速度大小为48.69 m/s,入口湍流度为0.03%,压力出口条件,翼段表面为无滑移壁面条件。外域与内域的交界面设定为interface条件,并处理成滑移界面对,两侧面为对称边界条件。采用UDF实现内域和翼段的俯仰运动,数值格式设定均为二阶,采用DDES方法进行计算,时间步长为0.001 s。
翼段以正弦规律进行俯仰运动,攻角变化规律为:
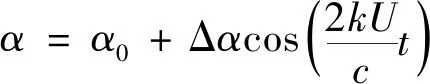
(1)
式中:α0为平均攻角;Δα为振幅;k为折合频率;U为来流速度;c为弦长;t为时间,取第4个计算周期的结果进行分析。
2 计算结果与分析
2.1 模拟方法精度验证
现有文献鲜有报道有关加涡流发生器的DU91-W2-250翼段动态失速试验结果,故无法通过试验数据来验证动态失速的数值模拟结果。本文通过加涡流发生器的DU91-W2-250翼段静态失速数值模拟结果与试验值[3]进行对比,来验证数值方法有效性,结果如图3所示。从图3可看出,加涡流发生器翼段升力系数计算值与试验值具有很好的一致性。涡流发生器使DU91-W2-250翼段静态失速攻角从10°延迟到17°左右,最大升力系数由1.4增大至近2.0。
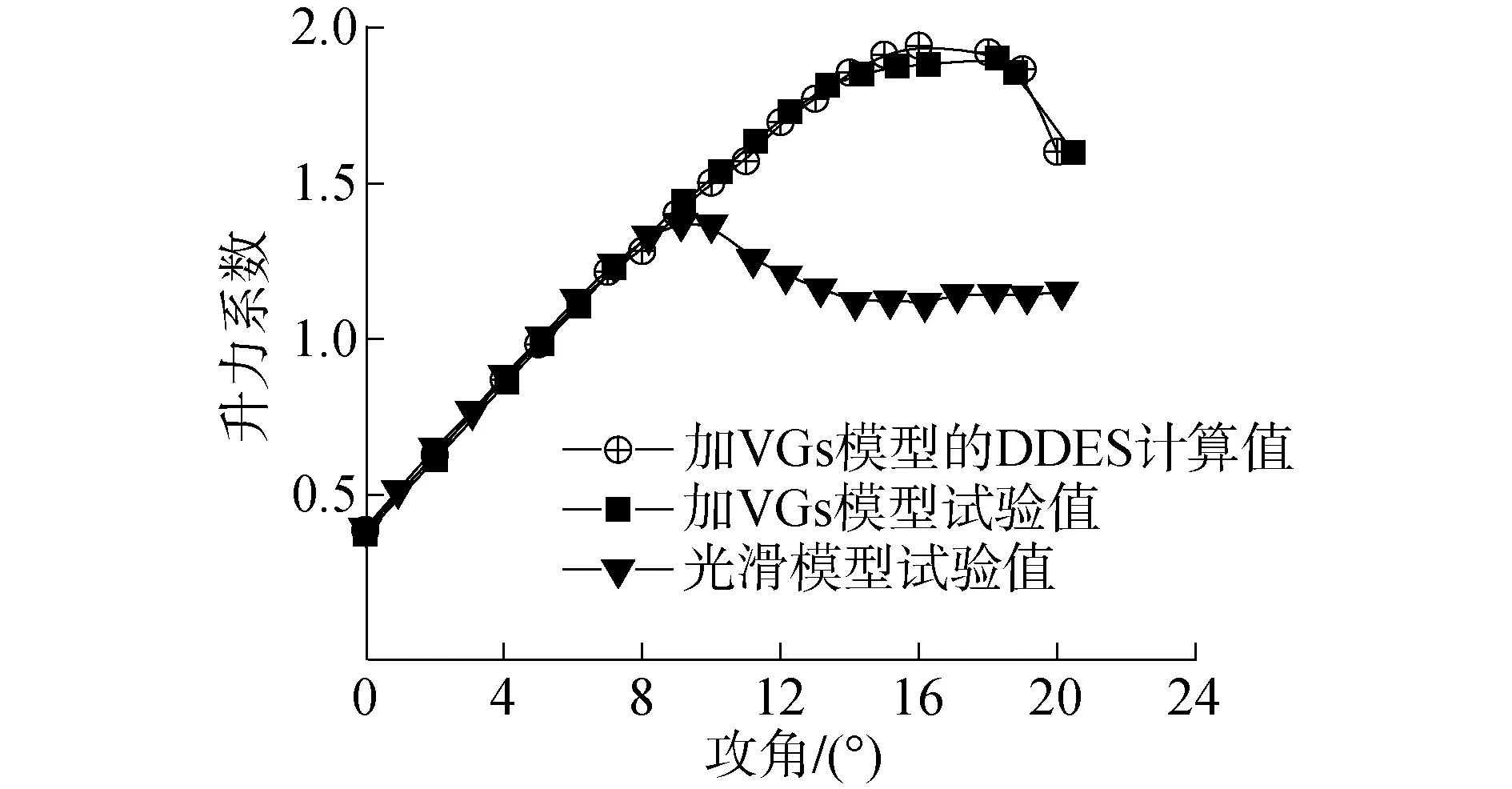
图3 DU91-W2-250翼段静态失速升力系数曲线Fig.3 Lift coefficient curve of DU91-W2-250 airfoil segment in static stall
2.2 涡流发生器对翼段静态失速的影响机理
图4为光滑翼段和加涡流发生器翼段在14°攻角下展向中心剖面流场图、速度型图和涡流发生器后某处叶尖涡涡量云图。从图4(a)、(b)可看出,光滑翼段后缘出现分离,加涡流发生器翼段上表面为附着流动。图4(c)、(d)为翼段展向中心剖面弦长位置x/c=50%、90%处的速度型对比。横坐标为x方向流速u相对与来流速度U的无量纲值,纵坐标为沿壁面法向距离Sn的高度相对弦长c的无量纲值。从图4(c)看出,x/c=50%处,光滑翼段表面流体为附着状态,加涡流发生器后的近壁面流动速度变大;从图4(d)看出,x/c=90%处,光滑翼段近壁面流动速度为负,表明x/c=90%处已发生流动分离;与x/c=50%处相比,加涡流发生器翼段边界层的厚度变大,没有反向流动产生,分离被抑制。这是由于涡流发生器能够产生图4(e)所示的叶尖涡,叶尖涡将主流能量传递到附面边界层流动中,增强边界层流体抵抗逆压的能力,起到延迟失速分离和增升减阻的效果[4]。

图4 翼段表面流动特性分析,α=14°Fig.4 Analysis of flow characteristics on blade section surface, α=14°
2.3 涡流发生器对翼段动态失速的影响
2.3.1 涡流发生器对深失速和轻失速流场的影响
图5为动态失速过程中光滑与加涡流发生器翼段典型攻角处展向中心剖面涡量云图对比。如图5(a)、(b)所示,深失速工况,上仰攻角为19.38°时,光滑翼段后缘处出现分离,加涡流发生器翼段表面流动未出现分离。如图5(c)、(d)所示,攻角达到最大值24°时,光滑翼段分离点已非常靠近前缘,存在明显涡脱落现象,加涡流发生器翼段分离程度相对较轻。如图5(e)、(f)所示,下俯攻角为12.40°时,光滑翼段的分离继续加重,加涡流发生器翼段表面的附着流动已重建。如图5(g)、(h)所示,轻失速工况与深失速不同,加涡流发生器翼段在最大攻角15°处仍未发生分离,涡流发生器完全抑制了光滑翼段的分离现象。
总的来说,深失速工况下,涡流发生器在上仰段延迟了翼段表面流动分离的发生,在下俯段加快了表面附着流动的重建,深失速过程中的分离现象被明显改善;轻失速工况下,光滑翼段分离程度较深失速更小,加涡流发生器后能够完全抑制分离现象的发生。
2.3.2 光滑翼段轻失速和深失速升阻力分析
图6分别为深失速与轻失速工况的升阻力系数迟滞曲线。从升阻力系数曲线可知,深失速工况在上仰大攻角阶段,翼段表面剧烈涡脱落现象导致了升阻力系数的剧烈波动,表明发生失速;轻失速工况下,失速在下俯段发生,升阻力系数曲线更加光滑平稳,表明轻失速的分离程度较小。
2.3.3 涡流发生器对深失速和轻失速气动性能的影响
图7为深失速工况下光滑和加涡流发生器翼段的升阻力系数迟滞曲线。如图7所示,上仰段,α<13°时,涡流发生器对升阻力系数影响较小,加涡流发生器翼段的升力系数略高于光滑翼段;α<10°的范围内阻力系数略低于光滑翼段值,这与涡流发生器在静态失速小攻角阶段表现不同,涡流发生器对后者产生增阻效果[2]。当α>13°后,加涡流发生器翼段升阻力系数均明显高于光滑翼段,增升减阻效果越来越明显,最大升力系数增加10%,最大阻力系数减少56.3%;而且涡流发生器抑制了光滑翼段
上仰到α>20°后的升阻力系数波动现象。下俯段,涡流发生器增升减阻效果更加显著,平均升力系数增加29.4%,平均阻力系数减少59%。

图5 典型攻角处的涡量云图对比Fig.5 Comparison of vorticity contour at typical angles of attack

图6 光滑翼段动态失速气动特性Fig.6 Aerodynamic characteristics of smooth wing segments during dynamic stall

图7 涡流发生器对深失速气动性能的影响,Fig.7 The effect of VGs on aerodynamic performance in deep stall, Δα=10°, k=0.078
图8为轻失速工况光滑和加涡流发生器翼段的升阻力系数迟滞曲线。如图8(a)所示,在上仰段,加涡流发生器翼段升力系数整体高于光滑翼段,最大升力系数增加13.7%;在下俯段,平均升力系数增加34.8%,且升力系数比上仰时更高,迟滞曲线成逆时针环状。这与深失速工况相反,后者下俯段升力系数较上仰段更小,迟滞曲线为顺时针环。这是由于深失速分离严重,加涡流发生器延缓了分离,下俯段仍存在分离现象;光滑翼段轻失速过程分离程度低,加涡流发生器后能完全抑制分离现象发生,使得翼段能够在下俯段表现出比上仰段更好的气动性能。如图8(b)所示,在上仰段,加涡流发生器翼段阻力系数α<8°时较光滑翼段更低,在α>8°时则高于光滑翼段,最大阻力系数增加约4%;下俯段,加涡流发生器翼段阻力系数明显低于光滑翼段,平均阻力系数减少32.2%。
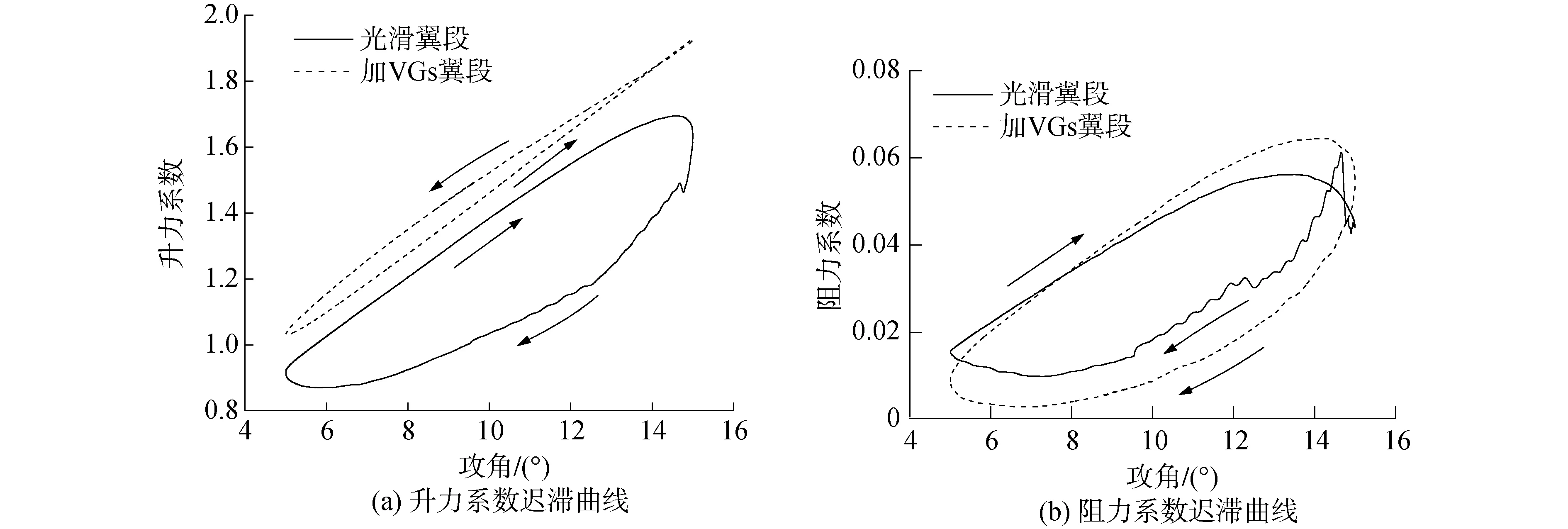
图8 涡流发生器对轻失速气动性能的影响,Fig.8 The effect of VGs on aerodynamic performance in light
图9为深失速和轻失速下光滑和加涡流发生器翼段平均攻角位置处展向中心剖面压力系数分布图。从图9(a)看出,深失速工况中,加涡流发生器翼段上仰14°的升力系数从1.71提升到1.79,增幅为4.7%,而下俯14°升力系数增加更明显,从1.09到1.64,增幅达50%。从压力系数分布可看出,上仰14°光滑和加涡流发生器翼段的压力分布较为一致;从下俯14°看,翼段加涡流发生器后上表面压强显著变小,分离现象导致的压力系数平台消失,下表面压强明显增大,气动性能显著提升。如图9(b),对轻失速工况有关现象与深失速工况相似,翼段加涡流发生器后在平均攻角10°位置处的升力系数增大,其中下俯10°气动性能的改善效果更加显著。
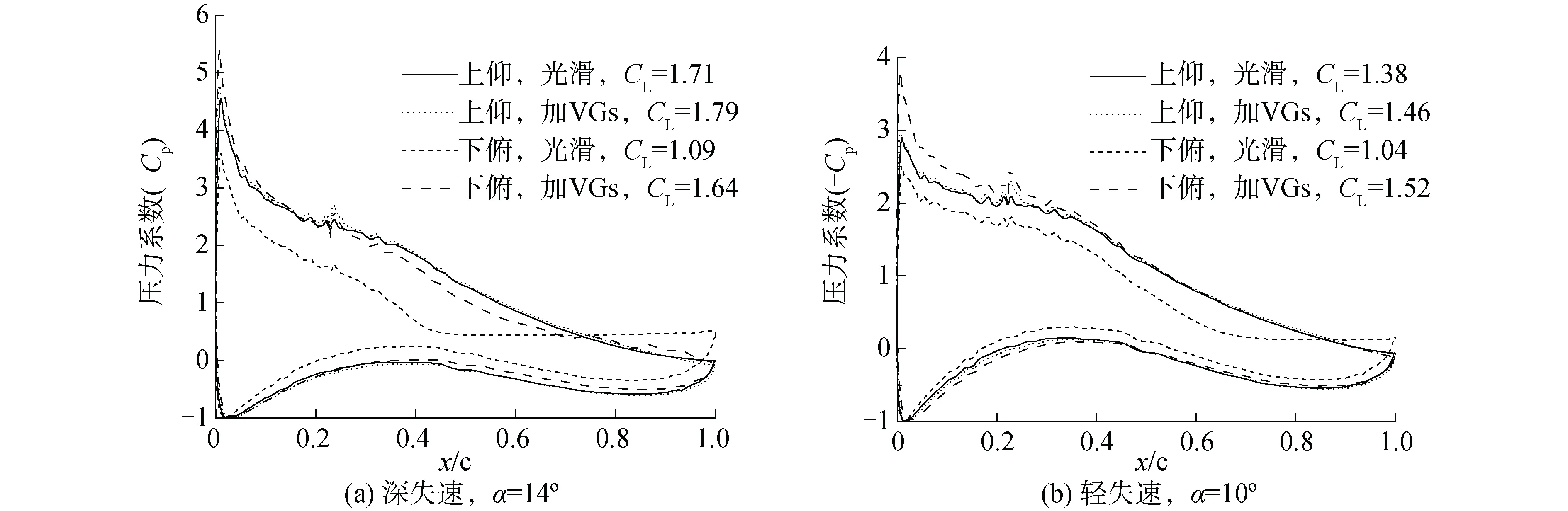
图9 压力系数分布Fig.9 Pressure coefficient distribution
由于分离程度不同,涡流发生器对翼段深失速和轻失速下升力的影响有明显不同。从图9平均攻角位置处升力系数大小可看出,轻失速工况翼段加涡流发生器后下俯10°升力系数要大于上仰10°,深失速工况翼段加涡流发生器后下俯14°升力系数要小于上仰14°。从平均攻角位置处压力分布看,相比深失速,轻失速工况中加涡流发生器翼段上表面前缘附近的下俯10°压力比上仰10°减小地更为显著,其余位置压力分布基本一致,而深失速工况中翼段上表面x/c为30%~70%的下俯14°压力比上仰14°明显更小。
从图9可看出,平均攻角位置处,深失速x/c=55%处和轻失速x/c=10%处加涡流发生器翼段下俯和上仰状态压力分布有较大差异,截取加涡流发生器翼段在平均攻角位置x/c=10%和x/c=55%处的速度型图,如图10。从图10中看出,在x/c=10%处,深失速和轻失速工况下俯状态速度均比上仰状态速度大,特别是在轻失速工况中。根据伯努利原理可知,加涡流发生器翼段上表面前缘附近下俯状态压力会比上仰状态压力更小,这现象在轻失速工况中表现地更加明显。在x/c=55%处,深失速工况中的上仰状态速度大于下俯状态速度。根据伯努利原理可知,深失速工况加涡流发生器翼段下俯状态压力大于上仰状态;而轻失速工况中两者速度相近,上仰状态和下俯状态压力基本一致。

图10 加涡流发生器翼段表面速度型图Fig.10 Velocity profile above blade segment surface with VGs
3 结论
1)涡流发生器能够抑制动态失速,表现为:对于深失速,涡流发生器能延迟翼段上仰段分离和加快下俯段附着,改善分离现象;对于轻失速,涡流发生器完全抑制了流动分离现象。
2)涡流发生器能够明显改善DU91-W2-250翼段动态失速下的气动性能,下俯段气动性能的提升效果比上仰段更显著。深失速下,翼段加涡流发生器后最大升力系数增加10%,最大阻力系数减少56.3%,下俯段平均升力系数增加29.4%,平均阻力系数减少59%。轻失速下,翼段加涡流发生器后最大升力系数增加13.7%,最大阻力系数增加约4%,下俯段平均升力系数增加34.8%,平均阻力系数减少32.2%。
3)由于深失速和轻失速的分离程度不同,涡流发生器对深失速和轻失速工况升力的影响不同,深失速下俯段升力系数小于上仰段,升力系数曲线为顺时针迟滞环,轻失速下俯段升力大于上仰段,升力系数曲线为逆时针迟滞环。
