相关能量分析中的后向检错方案*

1 引言

自1996 年Kocher 提出计时分析方法[1]以来, 侧信道分析这一不同于经典密码分析的独特密码分析方式, 经过20 多年的发展, 凭借其强大的分析能力及广阔的应用范围, 业已成为密码学界研究的热点. 侧信道分析的开展方式多种多样, 应用范围各有不同, 主要包括计时分析[1]、能量分析[2–4]、模板分析[5]、电磁分析[6,7]、碰撞攻击[8,9]、故障分析[10–12]、人工智能侧信道分析[13–15]等多种方式. 其中, 相关能量分析(Correation Power Analysis, CPA)[3]技术是侧信道分析领域最常用也是最有效的分析方式.

相关能量分析是Brier 等人[3]于2004 年提出的, 基本思想是利用密码设备运行时的能量消耗与其中间值之间的线性相关性, 通过猜测密钥, 计算中间值, 然后与采集到的能量波形求相关系数来判定此密钥猜测的正确性. 此法不仅效率远高于差分能量分析等传统方法, 而且实施简便、应用范围广, 不论是硬件密码芯片, 还是在CPU 中执行的密码算法程序, 都无法在无掩码等防护措施的情况下免疫此方法. 此法一经提出, 很快就取代了差分能量分析等第一代侧信道分析方法, 成为了侧信道分析领域应用最广泛的分析方法.

但是, 传统的CPA 方法也有其局限性, 由于其只使用一列点与猜测密钥生成的中间值的汉明重量/汉明距离求相关系数, 这就导致能量波形中大量其他的事实上也与密钥相关的点的信息被浪费了. 如果我们可以妥善利用这些信息, 则必然能够进一步提高分析效率, 降低对能量波形条数的要求. Oswald 等人[16]提出可以利用对应同一中间值的多个泄露点的信息, 按一定权重与中间值计算相关度, 以此提高效率, 减少恢复密钥所需的波形条数; Wang 等人[17]则更进一步, 提出利用AES 算法中S 盒输出值y 与列混合中会产生的2y、3y 中间值与其对应的波形共同求相关系数, 可以进一步提高CPA 的效率, 将所需的能量波形数减少80% 以上. 但是, 上述方案虽然利用了更多波形点的信息量, 然而其面对的共同问题是, 要想验证密钥猜测的正确性, 就必须恢复完整的密钥才行. 这时, 即使单个字节的密钥猜测准确率达到95%,完整恢复密钥的概率仍然只有44% 左右, 即使只错了一字节, 也只能否定整个密钥. 虽然有密钥枚举算法[18–20]可以利用CPA 产生的相关度序列对密钥空间进行有序遍历, 但是其搜索空间仍是整个密钥的范围. 如果能利用能量波形本身的特征来缩小搜索范围, 乃至判断某个子密钥猜测是否正确, 就可以极大地减小搜索空间, 甚至协助恢复密钥.

在文献[17] 的末尾, 作者提出了一种利用列混合处波形与对应中间值的相关系数判断密钥猜测是否正确的思想, 但未说明判断方法, 也未进行严谨地讨论. 受此启发, 我们提出了在进行标准CPA 之后, 利用列混合完成后的中间值与其对应的波形点求相关系数, 检验其对应的四字节密钥恢复是否正确的后向检错方案, 并依托此方案提出了一种基于阈值的四字节子密钥猜测正确性判别方案, 以此构建了一种能够将四个列混合分而治之, 四组子密钥分别恢复的密钥搜索方案. 经实验验证, 即使在单字节密钥猜测准确度不佳的情况下, 也可以将成功恢复密钥的概率提升至原先的两倍以上, 且能与各种对CPA 的优化方案无缝衔接.

本文余下部分的构造如下: 第2 节是预备知识, 主要介绍相关能量分析方法以及本文的分析对象: 世界上使用范围最广泛的分组密码算法—AES; 第3 节分两部分, 分别介绍了后向检错的基本原理以及基于此实现的基于枚举的后向检错算法; 第4 节为实验部分, 验证了阈值的存在以及算法的有效性; 第5 节总结全文, 并对下一步工作进行了一些展望.

2 预备知识

2.1 符号说明

lk密钥长度(字节)

lp明/密文长度(字节)

np明/密文数量

nt能量波形条数

lt各波形采样点数

k lk维行向量, 保存密钥

P np×lp矩阵, 按行向量形式保存明文

C np×lp矩阵, 按行向量形式保存密文

T nt×lt矩阵, 按行向量形式保存采集到的能量波形

Y np×lp矩阵, 按行向量形式保存明文通过白化密钥和字节代换之后的中间值

Z np×lp矩阵, 按行向量形式保存明文通过白化密钥、字节代换、行移位和列混合之后的中间值

ps单个字节密钥猜测准确率

ρS矩阵Y 中列向量与T 中列向量求得的相关系数

ρMC矩阵Z 中列向量与T 中列向量求得的相关系数

KeyCand 256×lp矩阵, 保存相关能量分析得到的按相关系数降序排列的候选密钥序列

Corr 256×lp矩阵, 保存与上述候选密钥一一对应的相关系数序列

2.2 高级加密标准

高级加密标准(Advanced Encryption Standard, AES)[21,22], 是一种由Joan Daemen 和Vincent Rijmen 设计的分组密码算法, 分组长度固定为128 比特, 密钥长度则可以是128, 192 或256 比特. 自2001 年被美国国家标准技术研究院选定, 接替超期服役十数年的DES 算法成为新一代标准算法以来, 经过近20 年的发展, AES 已然成为世界上使用范围最广的分组密码算法. 小到智能卡中的密码芯片, 大到国际互联网中的安全套接字层协议, 只要是需要保护数据安全的地方, 就有AES 的身影.

AES 算法主要由密钥扩展和轮函数两部分组成. 其中密钥扩展部分与本文工作关系不大, 以下主要介绍轮函数部分. 轮函数包含四个模块:

字节代换(SubByte) 利用GF(28) 域上的求逆和仿射变换实现的非线性字节替换操作, 又名S 盒;行移位(ShiftRow) 将16 字节输入视为4×4 矩阵, 对第i (0 ≤i<4) 行循环左移i 字节;

列混合(MixColumn) 将16 字节输入视为4×4 矩阵, 将各列左乘一个变换矩阵, 其中各元素的乘法和加法均在GF(28) 域上进行;

异或轮密钥(AddRoundKey) 将输入与密钥扩展所产生的轮密钥进行异或.

以AES-128, 即密钥长度128 字节的AES 算法为例, 其流程如图1 所示, 可见整个算法由白化密钥及十个依次执行的轮函数组成, 其中第10 轮不包括列混合部分. 图2 展示了隶属于同一列混合的四个字节的明文在第1 轮轮函数中经历的各项操作. 图中可见由于行移位操作的影响, 进入列混合的四个S 盒输出字节分别是y0、y5、y10和y15. 这四个字节经历了列混合之后, 将成为下一轮输入的前四个字节, 所以称它们为z0–z3. 中间值Y 和Z 将在后向检错方案中扮演十分重要的作用.

图1 AES-128 总体结构Figure 1 AES-128 structure

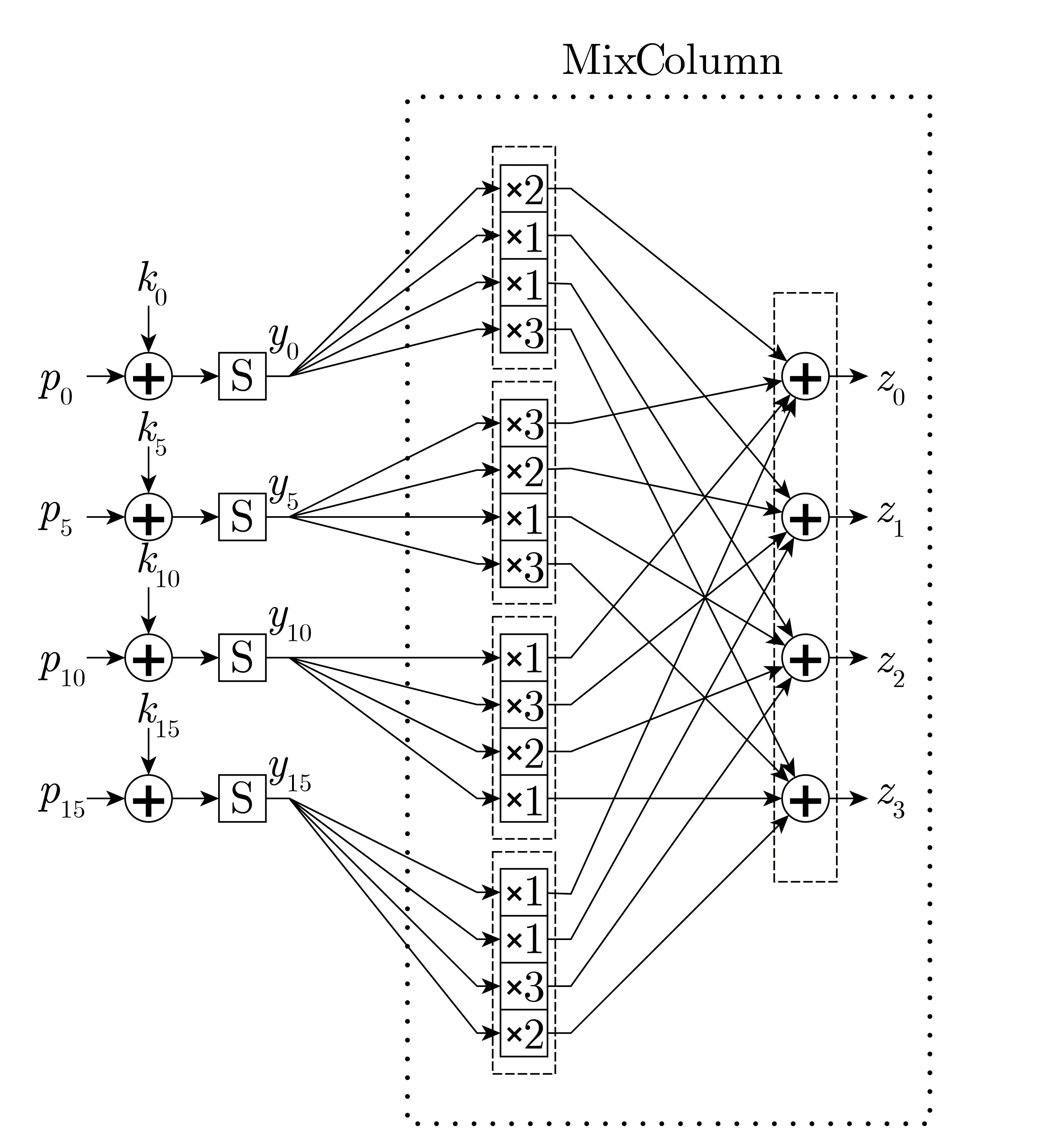
图2 第一轮细节Figure 2 Detail of first round

2.3 相关能量分析

相关能量分析[3]是侧信道分析领域广泛使用的经典算法,自2004 年提出至今始终是业界公认最为有效的侧信道分析方法. 此法是一种特殊的选择明文攻击, 目标一般是内部正在执行密码算法程序的CPU,即由软件实现的密码算法, 或是由数字电路硬件实现密码算法的集成电路芯片. 攻击者一方面需要拥有目标设备的访问权限, 可构造任意明文所对应的密文, 另外还需要知晓目标设备内部使用的密码算法类型,并需要能控制目标设备的外围电路, 以便采集其能量消耗. 基本思想是利用密码算法执行过程中产生的中间值与产生该值时的能量消耗的相关性来判断密钥猜测是否正确. 以下将以软件实现的AES-128 算法为例进行介绍, 此时lp= lk= 16, 中间值与能量消耗之间满足汉明重量(Hamming Weight, HW) 模型, 即其能量消耗与中间值的汉明重量线性相关.

2.4 密钥枚举方法

为了解决相关能量分析对侧信息利用率较低, 一旦密钥恢复失败便无能为力的问题, 提高密钥恢复的成功率,学界提出了多种方法[18–20],其中Veyrat-Charvillon 等人[18]提出的最优密钥枚举算法(Optimal Key Enumeration Algorithm) 最为典型. 此法是一种基于分治思想的确定性算法, 利用相关能量分析产生的256×16 个密钥的相关度序列, 将每字节对应的256 个相关度值分别归一化并降序排列之后, 分为八组, 组内按照各密钥候选值的相关度归一化值, 将面积1×1 的正方形切分成256×256 份, 从面积最大的矩形开始, 按照同行、列有方格在边界集中时，其他方格在此方格被搜索出队前不重复入队的原则构建边界集, 以此作为搜索序列. 再使用树状递归的方法, 依托两个字节的边界集, 依次构建四字节、八字节和十六字节的边界集以及搜索序列. 此方法巧妙地利用了相关能量分析的输出值信息, 将各候选字节的相关度值转化其恰为正确密钥的概率, 并给出了科学的枚举方案, 可有效降低找到密钥所需的搜索空间.

3 后向检错方案

在相关能量分析方法当中, 检验密钥猜测是否正确的方案只有一种, 即利用猜测的密钥对任意明文进行一次加密, 或者对任意密文进行一次解密, 观察其结果是否与正确密/明文相等. 显然, 此法的最大弊端就是必须在密钥完全恢复正确的情况下才能判定其正确性, 而就算密钥只有一字节出现错误, 其加密结果也必然是错误的, 而且攻击者无从确定错误的字节是哪一个, 只能对整个密钥空间进行搜索. 虽然有密钥枚举等方式进行协助, 但是如果有方法能推测出错误密钥的出现位置, 缩小搜索范围, 无疑可以大幅提升效率. 后向检错方案的设计目的正是完成这一任务.

3.1 后向检错方案的基本原理

如图2 所示, 在通过各个S 盒之后, 各中间值的下一站是列混合. 图中可见输入列混合的四个字节都参与到了每个输出字节的运算当中, 也就意味着只要有一个字节的密钥猜错了, 此处的所有字节都会受到影响. 而列混合运算也是要消耗能量的, 它的输出值的汉明重量也会反映在能量波形上, 也能与波形各列计算相关系数. 当密钥猜错时, 此相关度同样会比密钥猜对时更低. 以下称此相关度为ρMC. 那么, 应当如何利用此特性来缩小密钥搜索范围？探究这一问题之前, 我们可以先对错误本身的特性进行一些分析.

设单字节密钥猜测正确率为ps, 则根据二项分布原理可求出完整猜中密钥以及出现错误字节的概率.表1 展示了在单字节正确率为某值时, 出现某数量错误字节的可能性. 表中最后一列包括所有单字节错误以及出现两字节、三字节和四字节错误时, 错误字节落在同一列混合中的情况. 可见就算单字节恢复正确率达到95%, 完整恢复密钥的概率也仅有44%. 但是在此情况下, 错误出现在同一列混合中的概率, 已经达到了40%. 而当密钥恢复正确率进一步提高到97% 时, 可以发现就算只能恢复发生在同一个列混合中的错误密钥, 也能将总的密钥恢复成功率提高到61.43%+31.84% = 93.27%, 这无疑是一个很大的进步. 所以, 当单字节密钥猜测准确率较高时, 我们可以使用一种简单方法恢复大多数的密钥. 具体流程如算法1 所示.

表1 密钥错误字节数及其发生概率Table 1 Probability of number of wrong bytes

此方案可以确保当错误密钥确实只出现在一个列混合当中时, 攻击者可以准确找到此列混合, 并利用穷搜的方式恢复此密钥. 由于现代电脑计算能力的增强, 穷搜AES 的232密钥空间已不再是一个难以完成的任务, 即使在个人电脑上也只需要不到一小时即可完成. 但是, 只要错误字节分布在不同的列混合中,此法就断无可能恢复密钥. 为了解决此类同样常见的情况, 光靠现有的判断密钥恢复正确性的手段已经无法完成了, 我们需要更好的办法.

3.2 基于枚举的后向检错方案

如上所述, 简单后向检错方案仅能在ps≥95% 的情况下使用. 即使是ps的一点微小下降也会导致其成功率的暴跌. 其主要原因是此法仍然使用了利用加/解密结果正确性判断密钥猜测正确性的判别方式, 仅仅只是把容许的错误比特数量从零扩展到了同一列混合内的四字节而已. 如果有一种手段能够将正确和错误的列区分开的话, 就可以将标准CPA 中的分而治之思维运用到此处, 将四个列混合对应的密钥分别进行恢复. 实验发现, 可以采用阈值作为区分二者的标准. 另外, 为了提高搜索的效率, 我们利用文献[18] 中的密钥枚举算法, 对各列混合对应的四字节密钥进行枚举. 以下将分别介绍以上方法, 并将其组合成能对分散在多个列混合中的错误字节进行恢复的基于枚举的后向检错方案.

3.2.1 错误列判别

为了确定哪些列包含错误的字节, 攻击者需要确定一个阈值以区分正确和错误的密钥. 阈值可以通过观察简单算法中获得的各ρMC值进行估计. 在ps较高时, 出现四个列混合全有错的情况是极少的, 所以多数时候可以通过观察其最大值和最小值之间的差距来估计阈值的位置, 并且可以在恢复密钥过程中灵活调节. 如果四个列混合中只有一个列的ρMC值低于阈值, 则可以认为错误的密钥位于与该列混合相对应的四个字节中, 并且可以通过算法1 来恢复该密钥. 如果大于两个, 则通过加密结果判断密钥是否正确的方法将不再有效, 这时才需要利用基于枚举的方案.

3.2.2 密钥猜测正确性判别

如图2 所示, 列混合的计算仅与其对应的四字节密钥有关. 所以攻击者只需要猜测这几个密钥字节,就能获得列混合的中间结果, 而与其他密钥字节无关. 基于此种独立性, 上述阈值可用于估计猜测值的正确性, 即如果相应的ρMC高于阈值, 则此组密钥字节很可能是完全正确的. 但是, 以上思路有两点不足.首先, 一一计算所有232个ρMC显然是不可行的, 因为波形条数较多时, 相关系数的计算远比AES 算法本身更耗时; 第二, 既然恢复单个字节密钥时存在错误密钥的相关度高于正确密钥的情况, 那么类似的错误在此同样可能出现. 为解决上述两点不足, 我们采取了以下方法: 1、合理地安排候选密钥的顺序, 将具有较高正确概率的密钥字节先行猜测, 以提高搜索效率, 这即是密钥枚举算法的任务; 2、在枚举子密钥时,保存一些使列混合相关度超过阈值的子密钥, 形成候选子密钥集合, 枚举完毕后将各列混合对应的候选子密钥进行排列组合, 以此来提高找到正确密钥的概率.

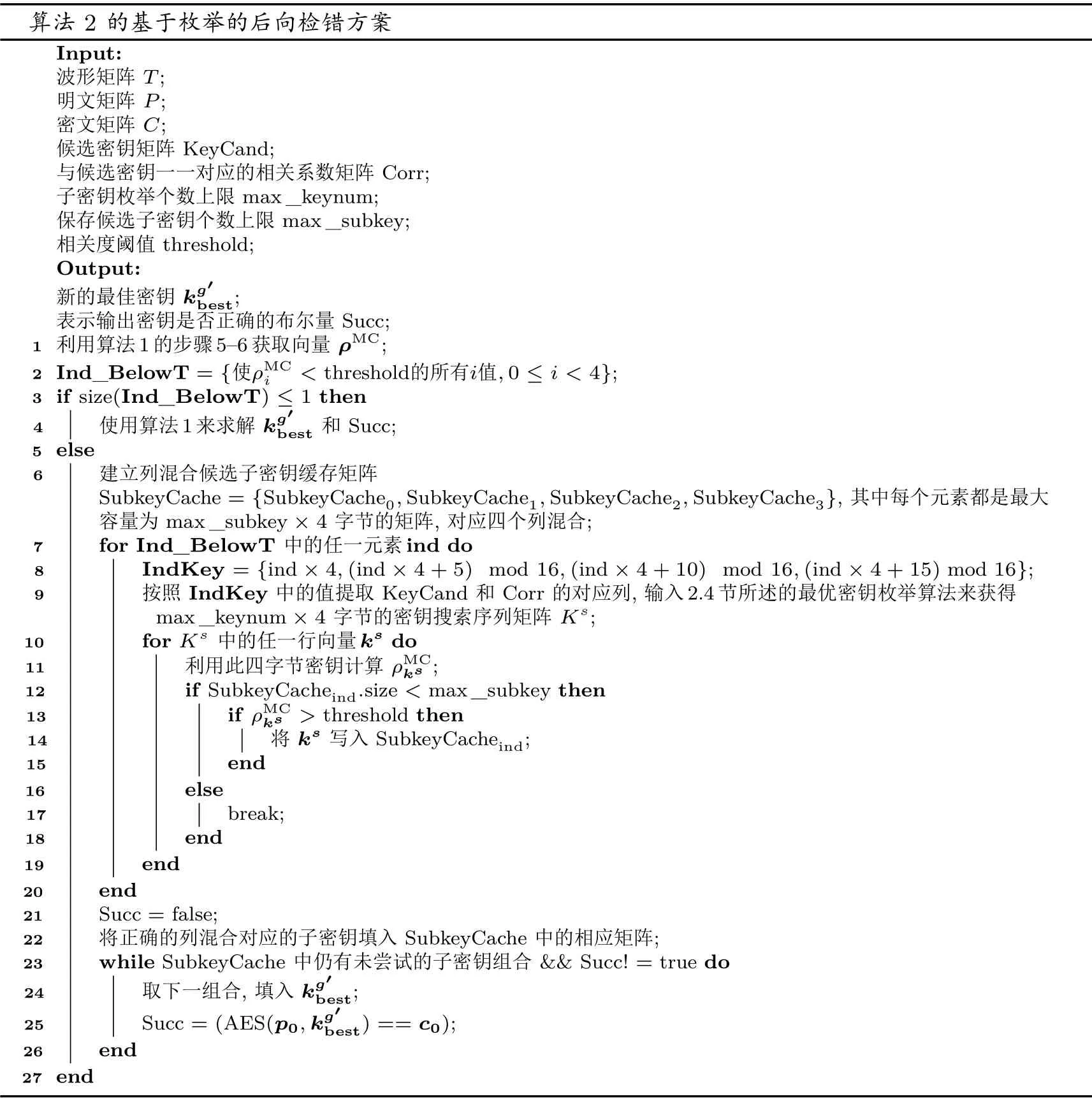
算法2 的基于枚举的后向检错方案Input:波形矩阵T;明文矩阵P;密文矩阵C;候选密钥矩阵KeyCand;与候选密钥一一对应的相关系数矩阵Corr;子密钥枚举个数上限max_keynum;保存候选子密钥个数上限max_subkey;相关度阈值threshold;Output:新的最佳密钥kg′best;表示输出密钥是否正确的布尔量Succ;1 利用算法1 的步骤5–6 获取向量ρMC;2 Ind_BelowT = {使ρMC i < threshold的所有i值,0 ≤i < 4};3 if size(Ind_BelowT) ≤1 then 4 使用算法1 来求解kg′best 和Succ;5 else 6 建立列混合候选子密钥缓存矩阵SubkeyCache = {SubkeyCache0,SubkeyCache1,SubkeyCache2,SubkeyCache3}, 其中每个元素都是最大容量为max_subkey×4 字节的矩阵, 对应四个列混合;7 for Ind_BelowT 中的任一元素ind do 8 IndKey = {ind×4,(ind×4+5) mod 16,(ind×4+10) mod 16,(ind×4+15) mod 16};按照IndKey 中的值提取KeyCand 和Corr 的对应列, 输入2.4 节所述的最优密钥枚举算法来获得max_keynum×4 字节的密钥搜索序列矩阵Ks;10 for Ks 中的任一行向量ks do 9 11 利用此四字节密钥计算ρMC ks ;12 if SubkeyCacheind.size < max_subkey then 13 if ρMC ks > threshold then 14 将ks 写入SubkeyCacheind;15 end 16 else 17 break;18 end 19 end 20 end 21 Succ = false;22 将正确的列混合对应的子密钥填入SubkeyCache 中的相应矩阵;23 while SubkeyCache 中仍有未尝试的子密钥组合&& Succ! = true do 24 取下一组合, 填入kg′best;25 Succ = (AES(p0,kg′best) == c0);26 end 27 end

3.2.3 密钥枚举

如2.4 节所述, 文献[18] 中给出的密钥枚举算法是自下而上构建搜索序列的, 也就是说此法不仅可以搜索完整的16 字节密钥, 对4 字节的子密钥也可使用. 我们只要提供相应字节对应的候选值-相关度序列, 就可以让算法按正确率从高到低的顺序输出密钥, 提供给上述正确性判别函数.

3.2.4 基于枚举的方案

有了以上基础, 就可以方便地建立起能够分别恢复各个列混合密钥的基于枚举的后向检错方案了, 其具体流程如算法2 所示. 需要说明的是, 虽然我们仍然需要对各列混合的候选子密钥集合进行排列组合,但是经过密钥正确性判别筛选之后, 我们只需保留10 到20 个候选值, 便可以较高的概率搜索到正确密钥, 其组合数目上限为105左右, 需要进行的计算量很小. 下文中我们以实验对算法的有消息进行了验证.

4 实验与对比

为了验证上述算法的有效性, 我们基于数缘科技的侧信道分析教学科研实验套件中的STC89C52 单片机、侧信道分析测评套件中的8 位和32 位CPU 智能卡三种场景进行了实验. 在以上三种设备之内,我们按照其设备特点分别实现了AES-128 程序, 主要差别是32 位卡中的列混合操作是利用32 位寄存器按列完成的, 即类似图2 中表现的那样, 而8 位卡和8051 单片机中的类似操作只能按字节完成. 这也就意味着在32 位卡上, 一个列混合对应的中间值是一个32 比特整数, 而在8 位卡和单片机上, 一个列混合对应四个8 比特整数, 二者不再对等. 考虑到如果密钥出错, 这四个字节的相关度都将下降, 所以我们采取的方法是直接将四个值的相关系数取平均值. 实验证明此法效果良好. 为确保实验的准确性, 我们在三种设备上均采集了5000 条固定密钥和随机明文, 包括整个第一轮的能量波形, 每次测试都随机从中抽取一定数量的波形来进行实验. 以下所有提到波形数量之处, 其波形均是如此抽取出来的.

4.1 阈值存在性检验

首先需要验证的是阈值是否存在. 此测试需要控制好参数, 使得各设备上的单个字节的猜测准确率ps基本相等. 在此测试中, 我们选择的ps值是0.9 左右. 为此, 我们将使用以下参数进行实验: 对于单片机,由于其电路集成度低, 功耗高, 能量泄露十分明显, 所以我们抽取13 条波即可达到此正确率; 对8 位卡,需要45 条波; 对32 位卡, 合适的波形数量则是50. 由于我们知道密钥, 所以可以在显示列混合相关度时标示出正确和错误的列混合. 测试效果如图3 所示.

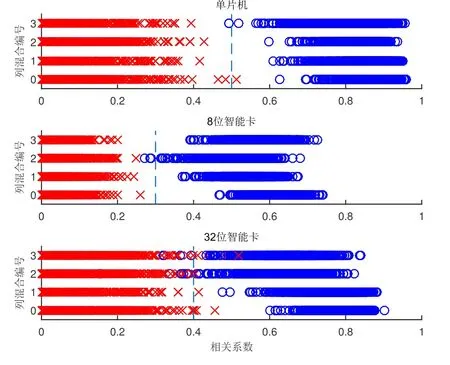
图3 三种设备对应能量波形的ρMC 分析Figure 3 ρMC analysis for power traces of three devices

“O” 形表示此列混合对应的子密钥完全正确, “X” 形反之, 各点的横坐标表示某一次测试时该列混合中间值与对应波形点的相关系数, 纵坐标为列混合编号, 图中竖向虚线标示了阈值. 根据之前的分析, 我们应当观察到绝大多数“O” 形点落在阈值右侧而绝大多数“X” 形点落在其左侧, 二者之间存在明显的分界.

图中可见, 虽然列混合之间有一定差异, 但是仍然只有极少数相关系数由于噪声的干扰而越过阈值,绝大多数相关系数值都落在了符合上述假设的位置上. 由此可见对三种实验设备而言, 列混合相关度的阈值均是存在的.

4.2 后向检错方案的效率对比

图4、5、6 展示了标准CPA、简单后向检错算法、枚举个数上限为216个的最优密钥枚举算法以及子密钥枚举个数上限为212个、候选子密钥上限为20 个的基于枚举的后向检错算法四种方案在各设备上的密钥恢复成功率, 另外列出了各点的单字节密钥猜测成功率ps作为参考. 图中横坐标为波形条数, 纵坐标对应1000 次实验的成功率. 其中单片机由于信噪比较高, 为确保其ps与智能卡大致相当, 故而使用的波形条数也相对较少. 值得注意的是, 由于基于枚举的后向检错方案存在候选子密钥排列组合的步骤, 所以我们采用了降低其子密钥枚举个数上限的方式来尽可能平衡复杂度差异.

图4 32 位智能卡波形的成功率对比Figure 4 Comparison of success rate of 32-bit smart card power traces

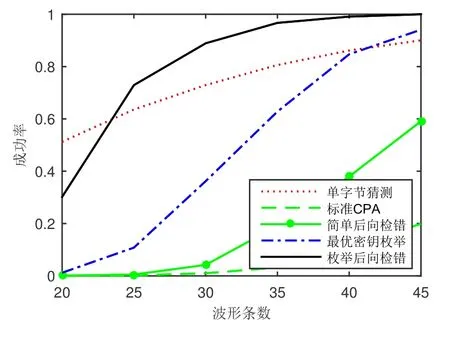
图5 8 位智能卡波形的成功率对比Figure 5 Comparison of success rate of 8-bit smart card power traces

图6 单片机波形的成功率对比Figure 6 Comparison of success rate of MCU power traces

图中可见, 不论在什么样的设备上, 简单后向检错和基于枚举的后向检错方案均比标准CPA 在成功率方面有显著提升, 而基于枚举的后向检错方案的成功率又比最优密钥枚举算法高出许多. 尤其是在ps低于80%的情况下, 此时就算使用密钥枚举算法也很难恢复密钥了, 而基于枚举的后向检错方案却仍能保持两倍以上的成功率, 这使得达到75% 成功率所需的能量波形减少了30% 到40%. 以上事实均说明基于枚举的后向检错方案确实起到了成功恢复多个列混合内的错误密钥字节的作用.

在时间方面, 基于枚举的后向检错方案由于需要进行较多的列混合计算, 所以必然比传统的最优密钥枚举算法要慢得多. 实验中的表现也确实如此, 在单字节正确率较低时, 最优密钥枚举算法完成搜索的平均时间约为0.021 秒, 而本方法则需要0.29 到0.95 秒, 视出错列混合数量而定, 从时间消耗上看确实差距较大. 但是侧信道分析主要的瓶颈出现在波形采集一端, 由于目标设备的访问控制、实际情况限制等诸多原因, 采集足量能量波形的任务不一定能够如期完成, 而只要得到了能量波形, 后续的分析工作完全可以不受干扰地进行, 时间方面并不存在瓶颈. 所以减少能量波形的使用量一般被视为侧信道分析方法优化的主要目标, 在这一点上本方案完全是合格的.

4.3 后向检错方案的适用范围

到目前为止的所有理论分析与实验均是以AES 算法为目标进行的, 但是由于现代分组密码算法结构的相似性, 利用攻击点之后的能量波形信息对密钥猜测值的正确性进行检验这一思路完全可以用在其他分组密码算法上. 以SM4 算法[23]为例, 此算法的轮函数中同样具有四个并列的8 比特S 盒以及以循环左移和异或组成的线性运算L(x)= x ⊕(x ≪2)⊕(x ≪10)⊕(x ≪18)⊕(x ≪24), 其中x 为位宽32比特的S 盒输出值. 此二者的组成恰与AES 中S 盒与列混合相对应, 所以我们的方法可以直接套用至软件实现的SM4 算法的侧信道分析中. 由于S 盒的位宽都是相同的, 所以连最优密钥枚举算法也可直接使用.

对其他分组密码算法也可用类似的方式进行处理, 只是可能需要调整密钥枚举算法而已. 如软件实现的DES 算法[24], 我们利用CPA 恢复首轮的子密钥后, 可以在本轮的P 置换、轮函数输出与明文的异或运算以及第二轮的E 置换等处进行后向检错, 由于DES 的位宽窄, 子密钥仅48 比特, 所以在执行后向检错时无需分治法也能达到比较好的效果.

5 结论

本文通过利用列混合处波形与中间值的线性相关关系, 设计了一种在相关能量分析完成后进行的后向检错方案, 能够在相关能量分析没能恢复密钥时, 寻找可能出错字节所对在的列混合, 缩小错误密钥字节的搜索范围, 最终对错误密钥进行修正. 方法是通过计算当前密钥猜测的列混合输出与能量波形的相关度,观察其是否越过阈值, 以此判断单个列混合对应的四字节子密钥猜测正确性, 再分别对各错误的列混合对应的四字节密钥分别进行搜索, 通过计算候选密钥产生的列混合输出与波形的相关性是否越过阈值来判断其正确性, 以此对各个出错的列混合分别进行修正, 而无需在完整恢复密钥之后才能得知其正确性. 另外,为了提高密钥搜索效率, 我们使用文献[18] 中的最优密钥枚举方法对单个列混合对应的四字节子密钥进行搜索, 提高了在232密钥空间中进行密钥搜索的效率. 上述方法极大地提高了密钥恢复成功率, 与最优密钥枚举方案相比, 在复杂度近似的情况下达到相同密钥恢复成功率时的能量波形使用量减小了30% 以上. 且适用于多种分组密码算法. 未来我们计划寻找更准确的区分正确与错误密钥候选值的方法, 使用能量波形中提供的更多信息, 以期找到更多有效的侧信道分析方法.