几类基于0-线性转换的置换多项式*
2021-03-19王丽莎
谢 茜, 王丽莎, 李 念
湖北大学 数学与统计学学院 应用数学湖北省重点实验室, 武汉430062
1 引言
设p 是素数, n 为正整数, Fpn 表示含有pn个元素的有限域. 若有限域Fpn 上的多项式F(x) 是从Fpn 到自身的一个一一映射, 则称F(x) 是Fpn 上的置换多项式. 平衡性是密码函数一项重要的安全性指标, 而有限域上的置换多项式能够有效地保证平衡性. 在密码算法设计中, 密码函数常由有限域上具有优良密码性质(如低差分均匀度、高非线性度、高代数次数等) 的置换构成. 基于置换多项式在密码学、编码理论和序列设计等领域的广泛应用, 构造新的置换多项式是一个值得深入研究的问题.
人们对置换多项式的研究已有150 多年的历史. 1863 年, Hermite[1]首先开创了对模素数p 的置换多项式的研究, 并提出了有限域Fp上置换多项式的一经典判别方法: Hermite 准则. 之后, Dickson[2]于1896–1897 年将置换多项式的概念推广到任意有限域Fpn上, 并对置换多项式作了深入探讨. 随后,越来越多的学者对置换多项式进行了研究. 目前, 已有利用迹函数和线性化多项式[3]、分段函数[4,5]、AGW 准则[6]等多种不同方法构造置换多项式. 2009 年, Coulter, Henderson 和Matthews[3]利用迹函数和线性化多项式构造有限域Fpn上的置换多项式. 同年, Charpin 和Kyureghyan[7]构造有限域Fpn上形式为G(x)+γ Tr(H(x)) 的置换多项式, 其中G(x) ∈Fpn[x], H(x) ∈Fpn[x], γ ∈Fpn, Tr(·) 表示Fpn上的绝对迹函数. 随后, Marcos 在文献[8] 中讨论形式为L(x)+γh(Tr(x)) 的置换多项式, L 为定义在Fpn上的Fp-线性置换, h(x) ∈Fp[x], γ ∈Fpn. 基于对以上形如G(x)+γh(f(x)) 的置换多项式的研究, Kyureghyan[9]提出由线性转换构造形式为L(x)+L(γ)h(f(x)) 的置换多项式F(x), 其中L 为定义在Fpn上的Fpm-线性置换, f(x) 为定义在Fpn到Fpm的函数, h(x) 为定义在Fpm到Fpm的函数, γ ∈F∗pn为f 的一个b-线性转换, m, n 为正整数, 且m|n. 同时, Kyureghyan 在文献[9] 中给出函数F(x) 为Fpn上置换的充要条件, 即对于某些适当的b ∈Fpm, x+bh(x) 为Fpm上的置换. 继而, Akbary,Ghioca 和Wang[6]将Kyureghyan 的构造推广到Fpn的任意子集上, 而不仅限于其子域上.

通过选择适当的函数f(x) 使F(x) 为Fpn 上的置换. 根据Kyureghyan[9]给出的结论, F(x) 在Fpn 上与g :u →u+bh(u) 在Fpm 上有相同的置换性质, 当b=0 时, g :u →u 为Fpm 上的置换, 此时F(x)为Fpn 上的置换. 因此, 通过找到存在0-线性转换的f 即可得到置换多项式F. 定义在Fpn 到其子域Fpm 上的函数能表示成如下迹函数的形式
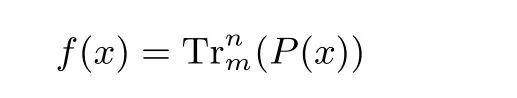
其中P(x) ∈Fpn[x] 且其不唯一[11]. 2017 年, Cepak, Charpin 及Pasalic[11]讨论了f(x) 为某些特殊稀疏多项式的情形及其存在线性转换所需条件. 本文主要考虑一类线性化多项式和一类二次齐次多项式f(x), 给出其存在线性转换所需满足的条件, 并进一步探讨其0-线性转换的存在性, 进而利用f 得到形式为(1)的置换多项式.
本文的结构如下: 第2 节给出一些预备知识; 第3 节主要讨论两类函数线性转换的存在性; 第4 节则讨论第3 节中两类函数存在0-线性转换的情况, 并构造两类形式为(1)的置换多项式; 第5 节总结全文.
2 预备知识
本节我们首先给出一些基本概念和相关已知结论.
定义1 设k, m, n 为正整数且满足n=km, f 为定义在Fpn到Fpm的函数. 令γ ∈F∗pn, 对于给定的b ∈Fpm, 若对任意的x ∈Fpn, u ∈Fpm均满足
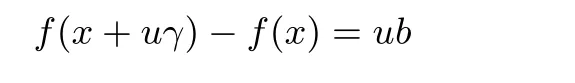
则称γ 为f 的一个b-线性转换. 特别地,当m=1 时,若对于任意的x ∈Fpn均满足f(x+γ)−f(x)=b,则称γ 为f 的一个b-线性结构.
定义2 设m, n 为正整数, m|n, 从有限域Fpn到Fpm的迹函数定义如下:
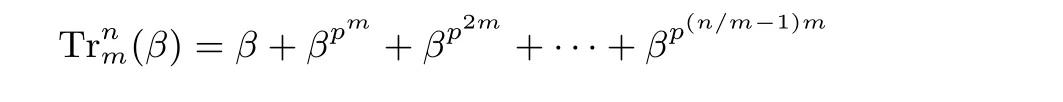
当m=1 时, 称其为Fpn 上的绝对迹函数.
定义3 设k, m, n 为正整数且满足n=km, 定义Fpn 上的Fpm-线性函数为
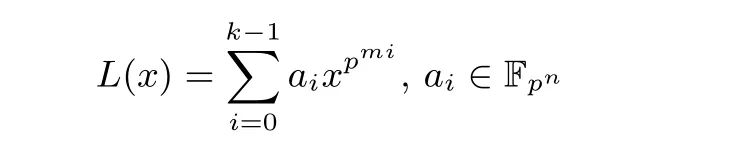
当L(x) 为Fpn 上的置换时, 则称其为Fpn 上的Fpm-线性置换.
关于形式如式(1)的多项式的置换性, 已有如下结论.

又因f(x)∈Fp, 则f(γ) 为Fp上的一个固定元, 故而, γ 为f(x) 的f(γ)-线性结构.
3 两类函数线性转换的存在性



4 置换多项式的构造
在第3 节的讨论中, 我们给出了一类线性化多项式和一类二次齐次多项式f(x) 存在线性转换的必要条件. 在本节中, 我们分别对下面线性多项式和二次齐次多项式f(x) 进行讨论:
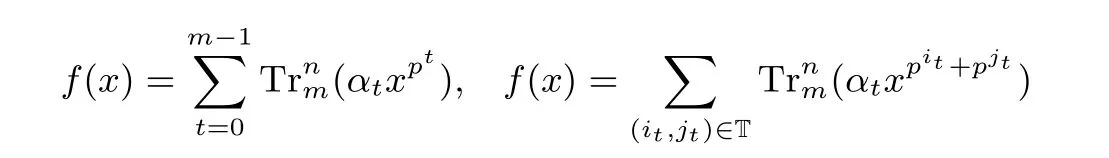
我们考虑f(x) 存在0-线性转换这一特殊情形, 此时g :u →u 为Fpm上的置换, 利用定理1, 我们可以得到形式为(1)的F(x) 为Fpn上的置换多项式.
首先, 我们讨论f(x) 是线性化多项式的情形.


且对任意的u ∈Fpm 有
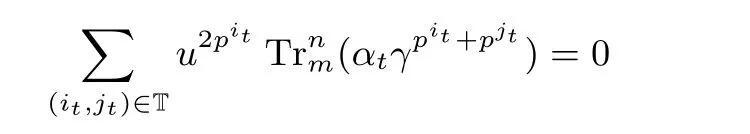
从而由题设条件可知, 满足条件的γ 为函数f(x) 的0-线性转换.
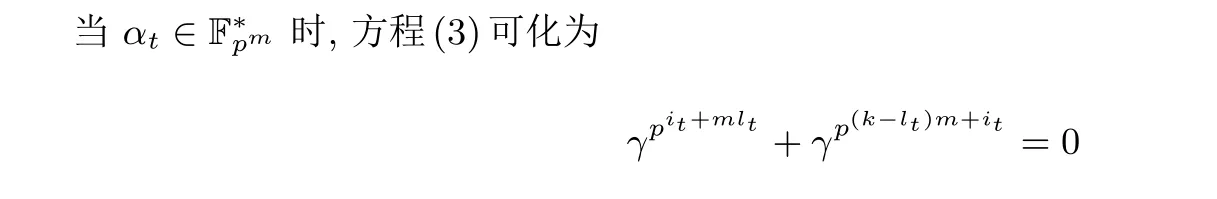
将等式两边分别同时pmlt−it次幂, 即可得γp2mlt−1=−1. 另一方面, 我们有
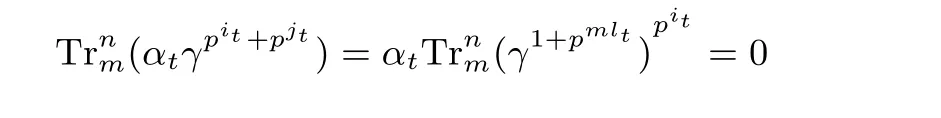
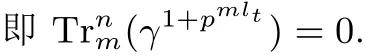

其中b1=a1+ml2, b2=a2+ml1, −k 证明: 由引理2 可知, f(x+uγ)−f(x) 与x 无关当且仅当 与x 无关. 由于pi1+pj1和pi2+pj2不属于关于pm模pn−1 的同一分圆陪集,即不存在整数−k 我们分以下三种情况讨论: (i) 若pi1, pj1属于同一分圆陪集且pi2, pj2属于同一分圆陪集, 则 由引理2 即可得证. (ii) 若pi1, pi2属于同一分圆陪集且pj1, pj2属于同一分圆陪集, 则存在整数−k 由等式(5)可得l1=l2. 此时, 上式(4)可化为 进而由引理3 和定理1 可推导出如下结论. 定理7 设k, m, n 为正整数满足n=km, L 为Fpn 上的Fpm-线性置换, h:Fpm →Fpm, 函数 且it, jt满足jt=it+mlt, −k 并且 本文讨论了从有限域Fpn到Fpm上的两类多项式(即线性化多项式和二次齐次多项式) 线性转换的存在性, 并通过深入研究其0-线性转换构造出了两类形式为式(1)的无限类置换多项式. 本文推广了Cepak 等人[11]的部分结论. 在本文的讨论中, 设计出形式为式(1)的置换多项式的关键在于确定存在线性转换的多项式f(x). 对于多项式f(x) 代数次数大于2 的情形, 讨论其线性转换的存在性可留做一个有趣的研究课题, 供读者思考.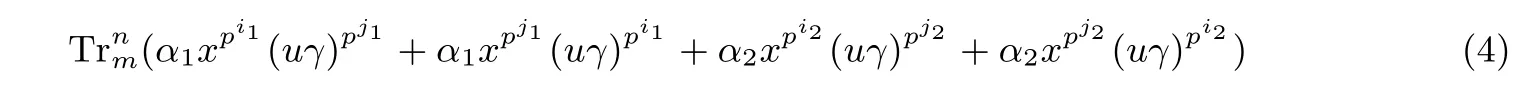

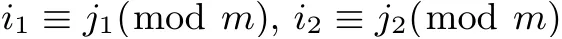
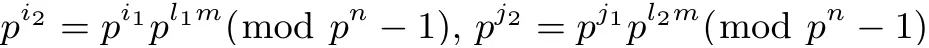


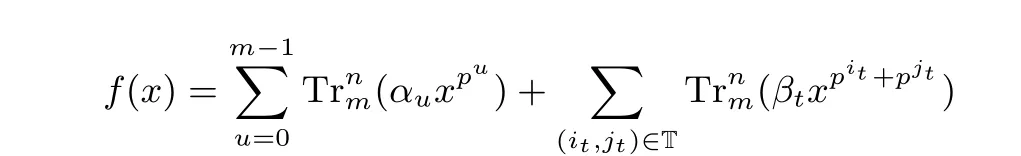
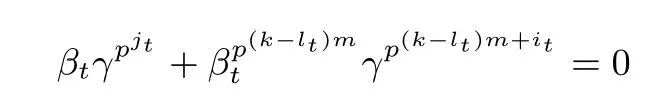
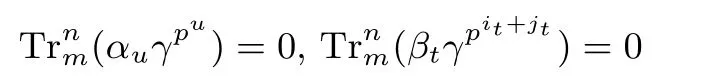

5 结论
