8 轮PRINCE 的快速密钥恢复攻击*

段春晖, 谭 林,2, 戚文峰,2

1. 中国人民解放军战略支援部队信息工程大学, 郑州450001

2. 数学工程与先进计算国家重点实验室, 郑州450001

1 引言

随着移动通信和物联网的发展, 射频识别系统(RFID) 和智能卡等设备的加密被广泛应用, 海量信息加密和有限资源处理间的矛盾日益突显, 传统的加密算法无法适用于资源受限的环境, 密码算法的轻量化越来越受到关注. PRESENT[1], SIMON 和SPECK 等[2]轻量级密码算法先后被提出, 它们使用小规模的密码组件, 在硬件实现方面有着明显的优势. PRINCE[3]密码算法是J. Borghoff 等在2012 年的亚密会上提出的一个轻量级分组密码, 它基于FX 结构[4]设计, 具有α-反射性质, 解密过程可以通过稍微改变密钥进行加密来实现. 这种特性使PRINCE 在硬件实现上具有优势, 但也使得其安全性受到担忧, H.Soleimany 等[5]针对某些特定的α 值在相关密钥模式下可以攻击全轮的PRINCE 变种, 但这里不包括PRINCE 算法的α 值.

学者们对PRINCE 算法的安全性进行了大量分析, 表1 罗列了目前在单密钥模式下对PRINCE 算法不同轮数版本的主要分析结果. J. Jean 等给出了4 轮和6 轮PRINCE 的积分攻击[6]. 王小云团队使用中间相遇攻击方法攻击了8 轮和9 轮PRINCE[7]. 虽然PRINCE 的轮密钥除了首尾白化外都相同, 但仍假设差分特征概率等于各轮差分概率的乘积, A. Canteaut 等[8]构造了5 轮和6 轮的多重差分区分器, 攻击了9 轮和10 轮PRINCE; 赵光耀等[9]给出了5 轮和6 轮的截断差分区分器, 并攻击了7 轮PRINCEcore. P. Derbez 等[10]将中间相遇方法和SAT 方法相结合, 攻击了10 轮PRINCE. P.Morawiecki 利用积分和高阶差分分析, 给出了4 轮至7 轮PRINCE 实际的攻击[11]. 随后, R. Posteuca等改进了6 轮PRINCE 的积分攻击, 降低了数据量和计算量[12]. 利用预存储技术, S. Rasoolzadeh 等改进了4 至6 轮的积分攻击和7 轮的高阶差分攻击[13]. L. Grassi 等利用子空间路径给出了只需要8 个选择明文的4 轮PRINCE 的截断差分攻击[14].

本文将文献[8] 的多重差分技术稍作改变, 考虑输入差分为固定值, 输出差分为选定的集合, 给出了目前轮数最长的7 轮PRINCE 区分器, 并对8 轮PRINCE 进行了密钥恢复攻击. 本文给出的7 轮差分区分器的概率为2−56.89, 8 轮PRINCE 的密钥恢复攻击所需的数据复杂度为261.89个选择明文, 时间复杂度为219.68次8 轮加密, 存储复杂度为215.21个16 比特计数器. 相比目前已知的8 轮PRINCE 密钥恢复攻击的结果, 包括将A. Canteaut 等的10 轮攻击方案减到8 轮, 本文的时间复杂度和D×T 复杂度都是最低的.

2 PRINCE 密码算法简介

图1 PRINCE 算法结构图Figure 1 Structure of PRINCE

将PRINCE 的64 比特状态X 看成一个4×4 的矩阵, 每一个块单元为4 比特, 本文中我们记X(l)为表示X 的第l 块, l ∈{0,1,··· ,15}, 块的顺序如图2 所示. 算法的轮函数可表示为R = AK ◦ARC ◦SR ◦M′◦S, 包括以下5 个变换:

图2 状态X 的16 个块标记Figure 2 State X

S 层: 16 个块同时查询一个4 比特的S 盒, S 盒如表2 所示.

表2 PRINCE 的S 盒Table 2 S-box of PRINCE

扩散层M′: 扩散层对应对角矩阵M′=diag( ˆM0, ˆM1, ˆM1, ˆM0), 作用在状态X 上为

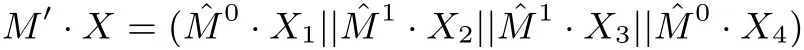
这里Xi表示X 的第i 列, 1 ≤i ≤4, 矩阵 ˆM0, ˆM1分别为:

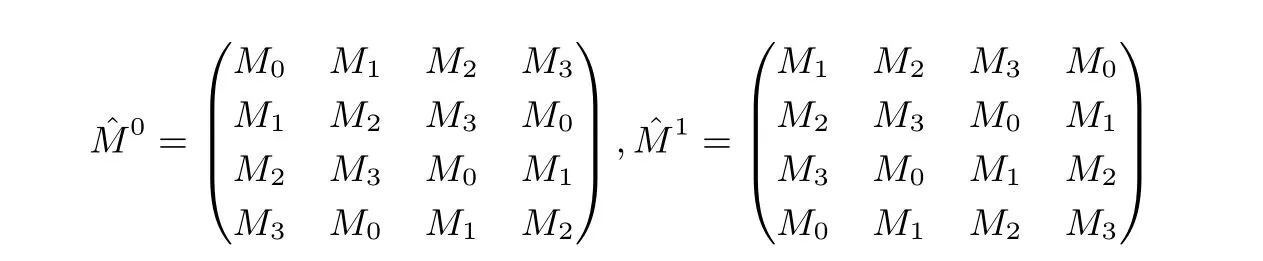
其中

行移位SR: 与AES 的行移位操作相同, 将状态的第i 行向左循环移动i 个块, 0 ≤i ≤3.

轮常数加ARC: 比特异或一个64 比特轮常数RCi,0 ≤i ≤11.

密钥加AK: 比特异或64 比特密钥k1.

3 准备工作

设∆in和∆out分别表示r 轮的输入差分和输出差分, 则r 轮差分概率

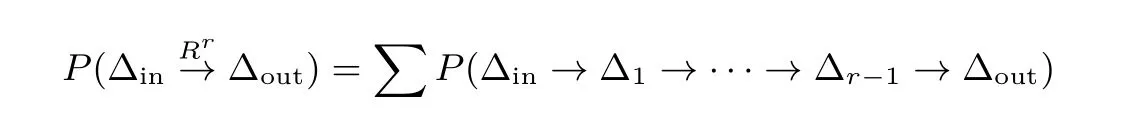
图3 差分模式∆i,i=1,2,··· ,8Figure 3 Difference pattern ∆i,i=1,2,··· ,8

文献[9] 指出了矩阵 ˆM0和 ˆM1具有如下性质: 如果δ ∈{1,4,5}, 则

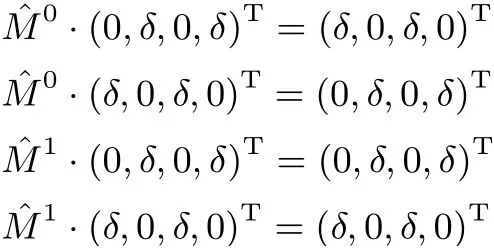
如果δ ∈{2,8,10},

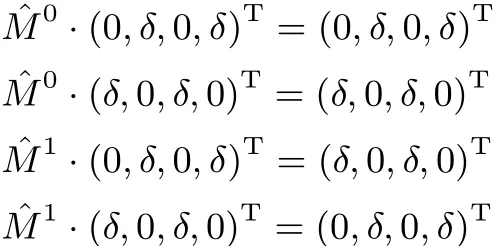
4 7 轮PRINCE 的差分区分器

由于轮密钥加和轮常数加不影响差分, 在下面的分析中我们将忽略这两个操作. 7 轮PRINCE 可以表示成:

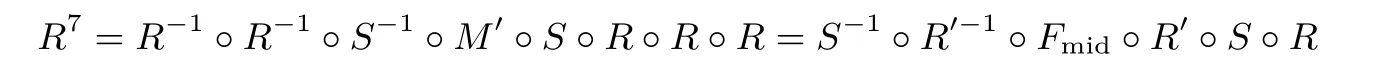
其中R = SR ◦M′◦S,R′= S ◦SR ◦M′,Fmid= M′◦SR−1◦S−1◦M′◦S ◦SR ◦M′. 为了计算7 轮PRINCE 在限定输入和输出差分集合的差分概率, 我们逐层考虑差分路径中各个节点的差分概率. 首先考虑R 层的输入差分集合

它们经过R 层的具体差分路径如图4 所示.

图4 R 层的4 条差分特征Figure 4 4 differential characteristics of R

由于扩散层中矩阵 ˆM0, ˆM1具有的特殊性质, 矩阵DR可以写成分块矩阵的形式:

其中

矩阵N 中有12 个值大于2−63, 也就是说我们得到7 轮PRINCE 的12×16 = 192 对概率大于2−63的差分, 由于计算时只使用了部分差分特征, 所以实际的差分概率要比DR7中给出的值更大.

5 8 轮PRINCE 的密钥恢复攻击

图5 8 轮PRINCE 密钥恢复攻击(ˆk)Figure 5 Key recovery attack on 8-round PRINCE(ˆk)

其中矩阵Z 为一个8×6 的矩阵:

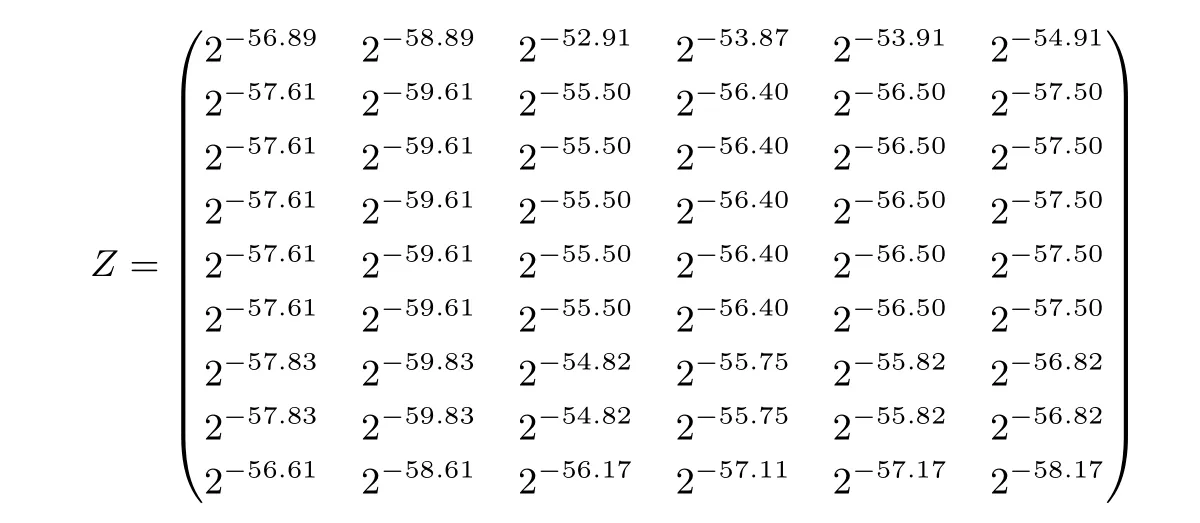
图6 8 轮PRINCE 密钥恢复攻击(k1)Figure 6 Key recovery attack on 8-round PRINCE(k1)

图7 应用文献[8] 区分器攻击8 轮PRINCEFigure 7 Attack on 8-round PRINCE using distinguisher given in Ref. [8]

6 结束语

本文利用改进的多重差分技术给出了目前轮数最长的7 轮PRINCE 区分器, 将其与随机置换区分需要数据复杂度约为257.89个选择明文, 计算复杂度约为256.89次密文异或. 利用此区分器我们给出了8 轮PRINCE 的密钥恢复攻击, 数据复杂度为261.89个选择明文, 时间复杂度为219.68次8 轮加密, 存储复杂度为215.21个16 比特计数器. 相比目前已知的8 轮PRINCE 密钥恢复攻击的结果, 包括将A.Canteaut 等给出的10 轮攻击方案减少到8 轮, 本文的时间复杂度和D×T 复杂度都是最低的. 能否将本文的攻击技术扩展到更高轮数将是我们后续研究的方向.