隐私保护的两方几何圆位置关系判定*
2021-03-19张明武张依梦
张明武, 张依梦, 谌 刚
1. 湖北工业大学 计算机学院, 武汉430068
2. 密码科学技术国家重点实验室, 北京100878
3. 桂林电子科技大学 计算机与信息安全学院, 桂林541004
1 引言
几何位置关系的判定在实际中应用非常广泛. 在军事系统中, 两雷达在不同范围半径进行位置探测,二者需要知道彼此探测区域的关系以判定是否彼此探测覆盖; 另外, 在社交网络中, 基于地理位置信息进行好友推荐, 并判断用户间的位置关系是社交网络的重要因素[1]. 随着大数据和人工智能等技术的发展,用户彼此间交互的信息量急速增加, 这可能造成用户信息的泄露[2,3]. 因此, 在参与多方有效判定各种位置关系的同时保护各自信息不被泄露是个不可忽视的问题[4].
安全多方计算(Secure Multi-party Computation, SMC)[5]为隐私保护的位置判定问题提供了有效的解决思路, 也为大多数学者的研究提供了一个重要方法. 安全统计分析[6,7]、安全几何计算[8,9]以及安全科学计算[10]等是常见的安全多方计算问题, 而隐私保护的几何位置关系判定问题, 是安全几何计算问题的核心问题之一. 针对该问题, 提出了具体的点与圆(多边形)[8,11–14]、点与直线[15,16]、及点与平面间[9,17]等位置判定的解决方案. Li 等人[14]提出隐私保护的点与凸(凹) 多边形位置关系判定协议, 首先提出的安全两方三角形面积计算协议, 然后通过判定三角形面积的符号位来解决凸多边形中的点包含问题. 基于文献[14] 中利用三角形面积判定的思想, Chen 等人[8]提出了点与凸多边形位置判定协议, 基于内积协议解决安全两方三角形面积计算问题, 然而该协议仅适用于解决凸多边形点包含问题. 而Zhang等人[11]提出利用高效的叉积协议以解决点与多边形的位置关系判定问题中, 其多边形可为任意多边形.文献[13] 中提出隐私保护的判定点与圆、点与凸多边形位置关系的协议, 用来秘密判定好友位置关系, 即用户选择任意范围, 通过与朋友进行安全的联合计算判断朋友是否在自己所选范围内, 且该协议采用安全两方余弦值计算协议, 避免了复杂的密码算法. 在解决隐私保护的点与直线间位置关系判定问题时, 利用安全内积协议来实现秘密点与秘密有向线间的位置判定由Yang 等人[15]提出, 而同态加密算法增加了其计算复杂度. Zhang 等人[16]提出保密判定点与线的位置关系协议, 该协议基于判定点是否为一个方程的解的思想并结合保密内积协议来解决该问题, 保密内积协议主要通过构造一个不可逆的矩阵来保护点与直线的隐私安全. 在解决隐私保护的平面间位置关系判定问题时, Li 等人[9]给出了隐私保护的判断点与平面的距离、直线与平面、以及两平面间的位置关系等问题的解决方案.
隐私保护的两圆位置关系判定中, 参与两方各自输入秘密的圆的半径和圆心等信息, 联合判定二方的位置关系且不会泄露各自输入的信息. 该类问题具有重要意义, 例如, 不同用户的社交圈中, 在不泄露自身好友信息的情况下判定是否具有共同社会交集且实现各用户社交信息的保密[18]. 为解决保密计算两圆公切线问题, Wang 等人[19]提出了安全计算两圆间的公切线协议, 并实现隐私保护的路径规划问题. Ye 等人[20]给出了计算两秘密输入的相交圆交点的协议. 文献[21] 提出了隐私保护椭圆相交判定方案. Liu 等人[22]基于安全两数和平方、安全两实数关系判定和安全两点距离计算等三个子协议提出安全两方圆计算协议, 然而, 他们只解决两圆相交、相离、外切三种关系的判定问题. 另外, 该协议需要多次调用子协议,所以这增加了系统的计算复杂度与通信开销. 针对以上提出的问题, 本文提出了一种新的方案以解决隐私保护的两圆间位置关系判定问题.
1.1 本文贡献
基于对传统的两圆位置判定方法的改进, 本文设计一个隐私保护的两方几何圆位置关系判定协议以实现安全的求解两圆间五种位置关系. 本文的主要贡献如下:
(1) 给出了隐私保护的欧几里德距离计算协议. 结合将Paillier 明文空间划分的思想以实现对解密结果进行正确映射, 提出了隐私保护的欧几里德距离计算协议, 提高了两方的计算效率.
(2) 提出一个隐私保护的两方几何圆位置判定协议. 基于隐私保护的欧几里德距离计算协议, 本文提出高效解决隐私保护的判定两圆位置关系问题的方案, 与相关方案采用不经意传输和内积协议相比, 本文方案具有较低的计算复杂度和通信开销.
(3) 支持判定两圆的五种位置关系. 除判定两圆相离、相切、相交三种位置, 本文协议还支持判定两圆内切、内含等位置关系.
2 预备知识
2.1 符号定义
为便于读者理解, 本节给出本文所用的基本符号.
κ: 系统安全参数
Pi: 协议参与方(i=a,b)
(pka,ska): Pa的Paillier 公私钥对
[[m]]: 消息m 的密文
(Sa,Sb): 半诚实模型下Pa,Pb的模拟器
ci: Pi拥有的几何圆
oi: ci的圆心
ri: ci的半径
(xi,yi): 圆心oi
2.2 两圆位置关系
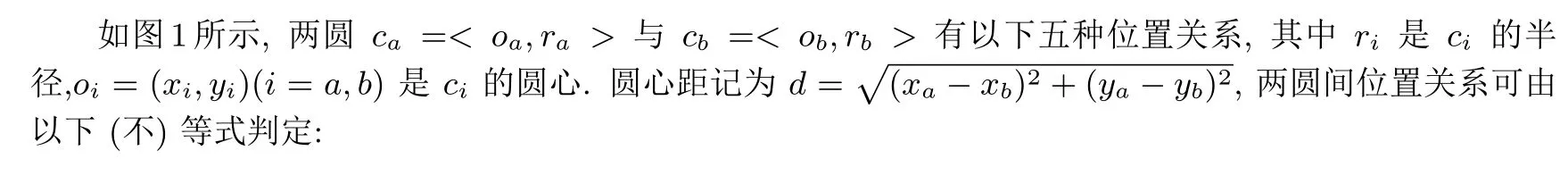
(1) 相离: d>ra+rb;
(2) 外切: d=ra+rb;
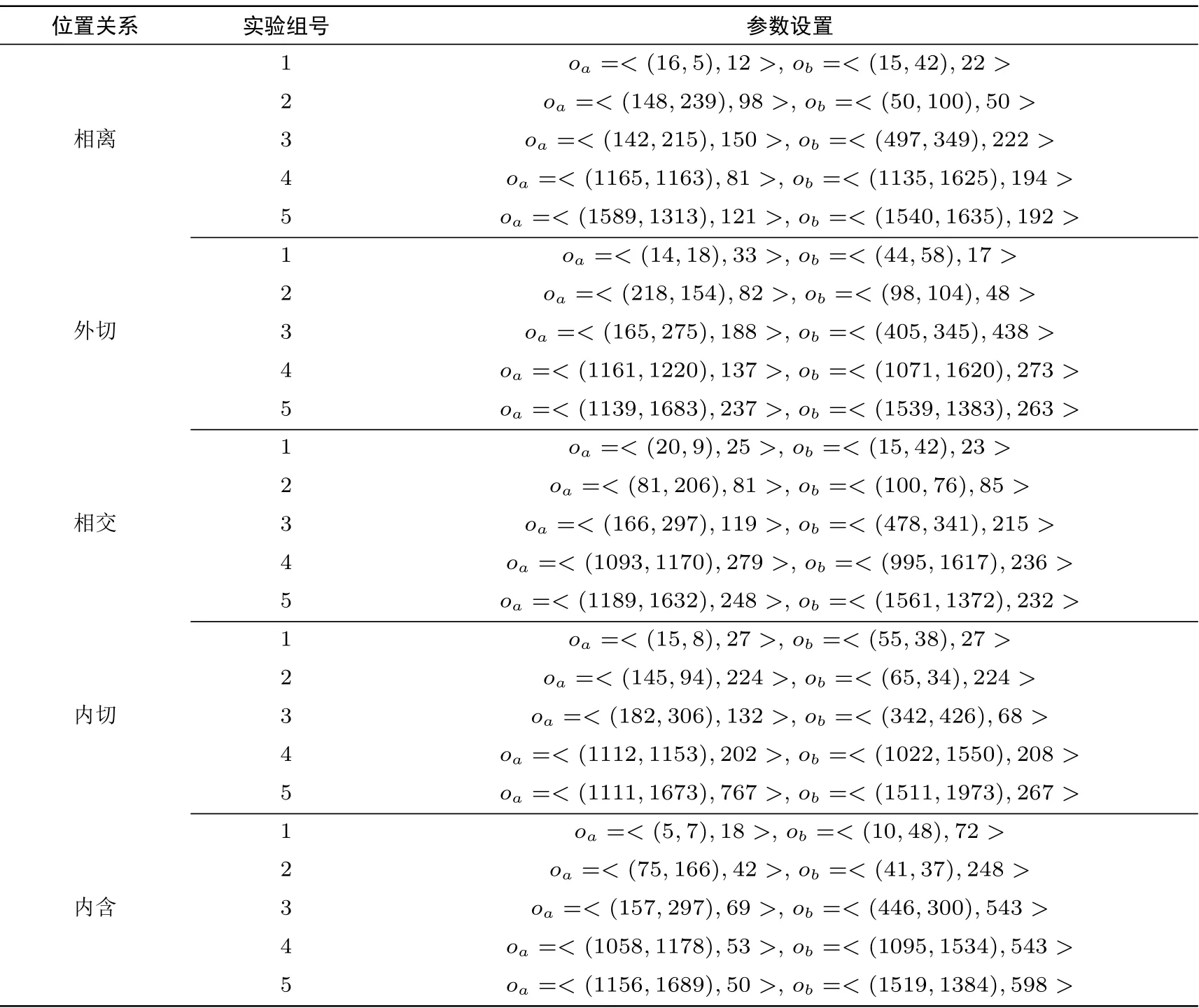
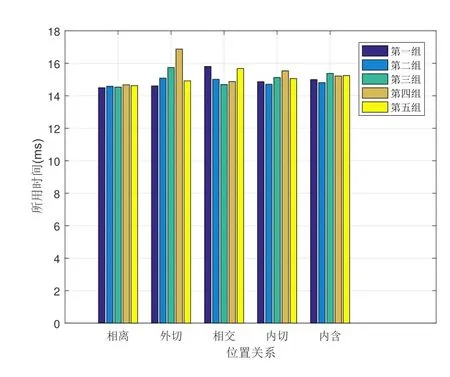
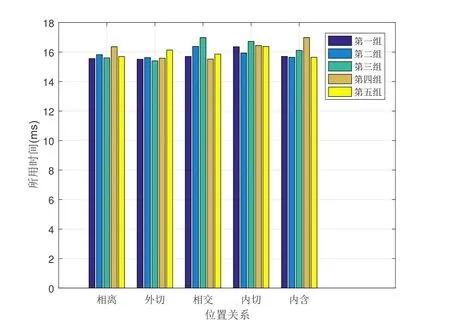
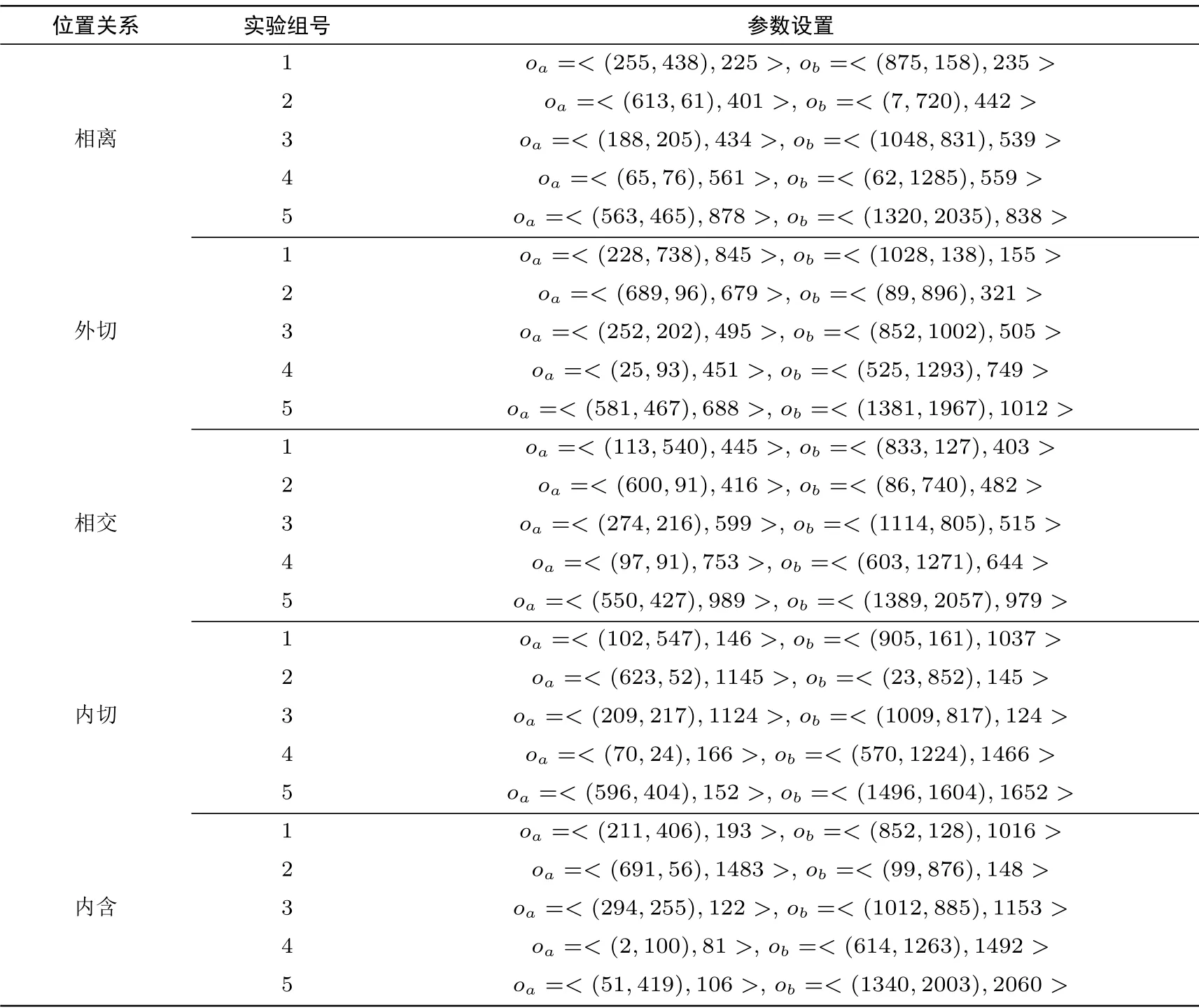
(3) 相交: |ra−rb| (4) 内切: d=|ra−rb|; (5) 内含: d<|ra−rb|. 为方便比较, 本方案将转化为计算d2=(xa−xb)2+(ya−yb)2. 在安全多方计算协议中, 敌手模型主要分为半诚实敌手模型与恶意敌手模型[23]. 由于本协议的参与方是半诚实的, 本文只给出半诚实模型及安全性定义. (1) 半诚实模型: 在半诚实模型下, 参与者能正确地执行协议, 在协议执行期间能得到所有中间结果,并试图根据所得的中间结果得到额外信息. 图1 两圆位置关系Figure 1 Positional relationship of two circles Paillier 加密算法是一种常用的加法同态加密算法[24], 对于明文空间的任意两个消息m1和m2的密文[[m1]] 和[[m2]], 以及随机数α(α ∈Zn), 该算法满足以下面性质: Paillier 加密算法包括三部分, 具体描述如下: • 密钥生成算法(Gen): 给定安全参数为κ, 生成两个大素数p 和q, |p| = |q| = κ, 且n = pq, 计算λ = lcm(p −1,q −1), 其中lcm(a,b) 表示两数a 和b 的最大公约数. 随机选取a ∈Zn, 置g =1+an(modn2), 定义函数L(x)=(x −1)/n. 置公钥pk=(n,g) 和密钥sk=λ. 定理1[25]Paillier 加密方案中不能直接对负数进行加密. 调用解密算法得到: 若要恢复出−m, 则需满足1+λkmn=1(modn2). 由于gcd(λ,n)=1, 则要求n|λkm. 通常k=κp,k=κq, 所以当m=0(modn) 才能正确解密消息,这与m 为负数相矛盾. 本文采用以下方法实现Paillier 中的负数表示及加密: 设明文空间为[0,n], 将其划分为两等长区间[0,(n −1)/2] 和[(n+1)/2,n], 将[0,(n −1)/2] 内代表正数, [(n+1)/2,n] 内代表负数. 对于待加密明文范围是[−(n −1)/2,(n −1)/2], 若待加密明文范围是[−(n −1)/2,0], 则转化为加密−m+n=n −m. 则加密过程表示为: 解密过程表示为: 协议1 隐私保护的欧几里德距离协议, 具体协议如图2 所示. 在初始阶段, Pa通过安全参数κ 产生一对Paillier 公私钥对(pka,ska), 将公钥pka发给Pb, 保留私钥ska. Pa方解密c 后的解密结果记为m′. 根据所述编码方式, 判断m′的取值范围, 得到正确的解密结果m. 若m′∈[0,(n −1)/2], 则m=m′; 反之, 若m′∈[(n+1)/2,n], 则m=m′−n. 进一步, 图2 协议1: 隐私保护的欧几里德距离计算协议Figure 2 Protocol 1: Privacy-preserving calculation protocol of Euclidean distance 本节在隐私保护的欧几里德距离计算协议基础上, 提出两圆间位置关系的隐私保护条件下的判定协议. 本节给出隐私保护的两圆间位置关系判定协议具体实现过程, 该协议是基于2.4 节提到的隐私保护的欧几里德距离计算协议. 协议2 隐私保护的两圆间位置关系判定协议, 如图3 所示. 图3 协议2: 隐私保护的两方几何圆位置关系判定协议Figure 3 Protocol 2: Privacy-preserving positional determination protocol of two geometry circles 协议2 实现过程如下: 输入: Pa输入ca= 输出: Pa和Pb均知道ca和cb的位置关系, 但是不知道彼此额外的信息. 说明: 输出结果记为flag, flag=1,2,3,4,5 分别表示两圆相离、外切、相交、内切、内含的位置关系. 步骤1: Pa运行Paillier 密钥生成算法, 生成一对公私钥对(pka,ska), 将pka发送给Pb, 保留ska. 步骤2: 基于隐私保护的欧几里德距离计算协议, Pa用pka加密ca的圆心(xa,ya), 计算如下: 将 步骤3: Pb收到 Pb利用自己坐标值(xb,yb) 在密文上计算下式: Pb将 步骤4: Pa用ska解密c24, 解密结果记为m. (1) 若f1>0, ca和cb相离, flag=1; (2) 若f1=0, ca和cb外切, flag=2; (3) 若f1<0, f2>0, ca和cb相交, flag=3; (4) 若f2=0, ca和cb内切, flag=4; (5) 否则, 若f2<0, ca和cb内含, flag=5. Pb将flag 发送给Pa, Pa和Pb均得到判定结果. 为证明协议2 的正确性, 本文需要对以下两点进行证明:Paillier 算法的加法同态性计算得到c24, 即 该协议安全性要求, 半诚实的两方Pa和Pb在共同执行完该协议后, Pa没有泄露圆ca的信息, Pb没有泄露圆cb的信息. 定理2 协议2 保密地实现圆ca与圆cb之间的位置关系. 证明: 由于该判定协议的输出为f(ca,cb) = fa(ca,cb) = fb(ca,cb) = flag, fa(ca,cb) 和fb(ca,cb)分别为Pa和Pb执行该协议后所得的结果, 这里分别构造Pa方的模拟器Sa和Pb方的模拟器Sb, 使其分别满足式(1)和式(2). 1) 构造模拟器Sa来模拟Pa去执行协议的过程如下: (4) Pb计算后得到判断结果, 记为flag∗, 并发给Sa. 在协议执行过程中, 我们得到: 又因为fb(ca,cb)=OUTPUTb(ca,cb), 故下式成立: 2) 构造模拟器Sb模拟Pb去执行协议2, 过程如下: 又因为fa(ca,cb)=OUTPUTa(ca,cb), 故下式成立: 综上, 由1) 和2) 可知, 协议2 在半诚实模型下是安全的. 本文运用Paillier 同态加密技术提出隐私保护的欧几里德距离计算协议, 对该协议进行扩展, 我们提出了隐私保护的两方几何位置判定协议(即协议2). 本节主要对协议2 进行性能分析. 协议2 设计安全两方模型解决两圆位置判定问题, 并运用Paillier 保证协议的安全性, 分析协议2 的计算复杂度时, 这里只考虑Paillier 算法加密操作、解密操作以及模幂操作的执行次数. 由此, 协议2 中Pa方需要执行2 次加密操作和1 次解密操作, Pb方需要执行3 次加密操作和2 次模幂操作, 即协议2 需执行5 次加密操作, 1 次解密操作以及2 次模幂操作. 通信开销 协议2 需要进行2 轮通信, 且Pa方需要发送两个密文和待比较数l0(明文空间内), Pb方需要发送一个密文和判断结果flag. 若安全参数是512, 假设待比较数l0的长度为256 bits, 则执行该协议的通信开销为6400 bits. 实验分析 协议2 解决了隐私保护的两圆间位置关系判定问题, 所判定的相对位置关系为相离、外切、相交、内切和内含等五种, 为分析各种位置关系下协议2 的执行情况, 本文对协议2 进行了仿真实验. 仿真实验的运行环境如下: Windows 10 64 位操作系统, 内存为8.00 GB, 处理器为Inter(R) Core(TM)i5-8250U CPU @1.60 GHz 1.80 GHz, 使用java 语言在IntelliJ IDEA 上运行的. 在实际情况中, 待判断的两圆可能距离很近也可能距离很远, 且两圆均有以下五种位置关系: 相离、外切、相交、内切与内含, 为充分分析协议2 在各种情况下的性能, 我们的仿真实验分如下两种情况进行: 情况一: 两圆相距比较近; 情况二: 两圆相距比较远. 具体来说, 本实验主要从两个方面展开: 一是协议2 在情况一下两圆位置分别为相离、外切、相交、内切以及内含时的性能; 二是协议2 在情况二下两圆位置关系分别为以上五种时的性能. 为便于理解, 本文对情况一和情况二的参数分别设置为0 本实验所选取的Paillier 加密算法的安全参数为512, 表1 和表2 是两种情况下各种相对位置关系仿真参数, 表中的第一列给出五种位置关系, 第二列给出每种位置关系下五组参数的实验编号, 第三列中对于每组位置关系随机选取5 组仿真参数, 这5 组参数是根据圆心距增大来进行选择的, 其中表中的参数列表示: oa=<(xa,ya),ra> 和ob=<(xb,yb),rb>. 根据表1 和表2 中所给的参数, 我们对每组参数进行1000 次的仿真实验, 并取其平均值, 实验结果如图4 和5 所示. 图4 和图5 从两个方面进行比较, 一是对于相同组数据, 比较各种位置关系下的性能, 二是对于同种位置关系, 比较每组参数下的性能. 表1 的第一组参数到第五组参数中, 圆心距逐渐增大. 图4 中显示, 在情况一下, 随着圆心距的增大,相对于位置关系为外切或相交时, 两圆相离时协议2 的执行时间波动不大, 并且当两圆相距极近时(如第一组), 每种位置关系下的第一组时间未呈现最低值. 另外, 在同组仿真参数下, 位置关系为外切时的总时间总是大于相离时的总时间. 图5 为情况二下五种位置关系是每组参数执行的总时间. 从图5 中看出,对于位置关系分别为相离、外切、相交、内切以及内含时, 第一组到第五组参数下执行协议2 的总时间未呈线性增长, 同时两圆相距较远时(如第五组), 执行总时间未呈现最大值, 且相同组参数在不同位置关系时执行的总时间均相差不大. 图6 给出了两圆相隔较近以及相隔较远两个情况下, 五种位置关系时协议2 的总时间比较. 从表6 可看出, 在情况一与情况二下, 相对位置分别为相离、外切、相交、内切和内含时, 协议2 执行时间相差较近, 且总时间均低于18 ms, 计算效率高. 综上, 两圆在相距较近和相距较远的情况下, 改变两圆相对位置关系均不会使协议2 的总时间呈线性增长. 圆心距相差较小时, 不同相对位置关系下协议2 执行时间相差小; 在两圆相距较近或相距较远的情况下执行协议2, 增大两圆间的圆心距的同时保持两圆相对位置关系不变, 协议2 的总时间未随圆心距的 增大而增加. 由此, 协议2 在两圆相距较近和相距较远的情况下来解决两圆相离、外切、相交、内切和内含等位置判定时均适用, 且执行总时间不高. 表1 情况一下五种相对位置关系仿真参数表Table 1 Simulation parameters of five kinds position relationship in Case 1 图4 情况一中五种位置关系时每组参数执行总时间Figure 4 Running time of each group of parameters in five position relationships in Case 1 图5 情况二中五种位置关系时每组参数执行总时间Figure 5 Running time of each group of parameters in five position relationships in Case 2 表2 情况二下五种相对位置关系仿真参数表Table 2 Simulation parameters of five kinds position relationship in Case 2 针对隐私保护的位置判定问题, 本文通过运用Paillier 同态加密技术, 并将Paillier 明文空间划分为两等长区间以实现对解密结果进行编码的方法, 给出了隐私保护的欧几里德距离计算协议. 基于该协议,我们提出一个隐私保护的两方几何圆的位置关系判定协议, 该协议避免圆心距分别与半径和、半径差间的直接比较, 将问题转化为与一方半径的比较. 另外, 与已有的保密判定两圆位置关系协议比较, 除了判定两圆相离、外切、相交外, 本文的协议还支持判定两圆内切、内含等位置关系. 实验分析表明, 在两圆相距较近与相距较远的两个情况下判定以上五种位置关系, 本文的协议均适用, 并具有计算复杂度不高和通信开销低等优势. 此外, 在后续的工作中, 本文的协议可扩展为解决隐私保护的两球体间位置关系判定问题.2.3 安全模型
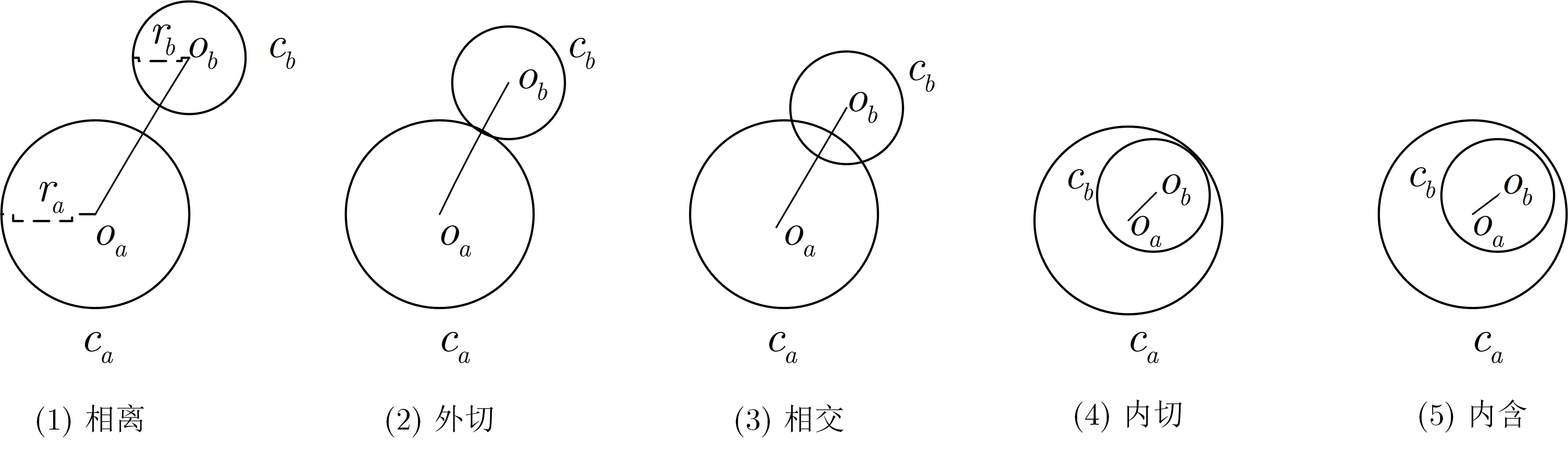

2.4 同态加密算法
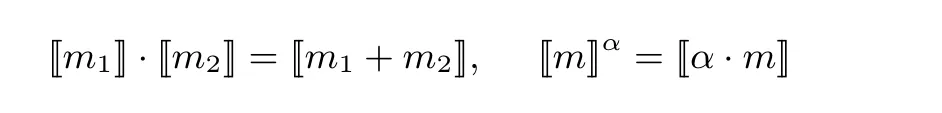
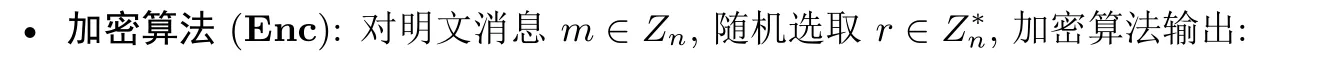
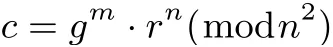

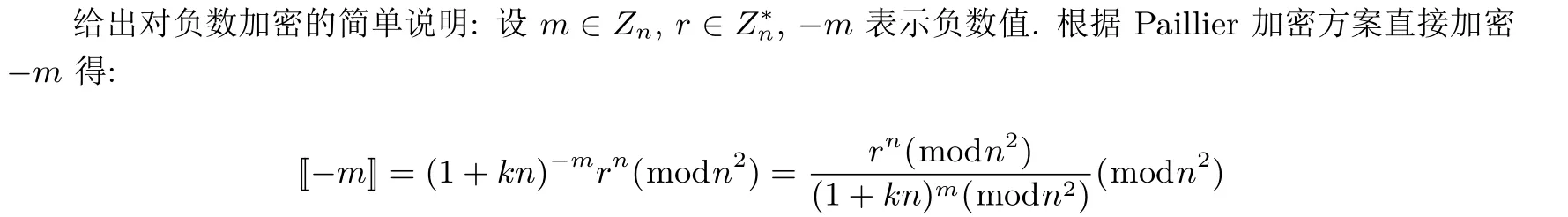

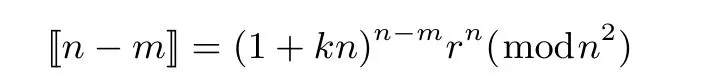
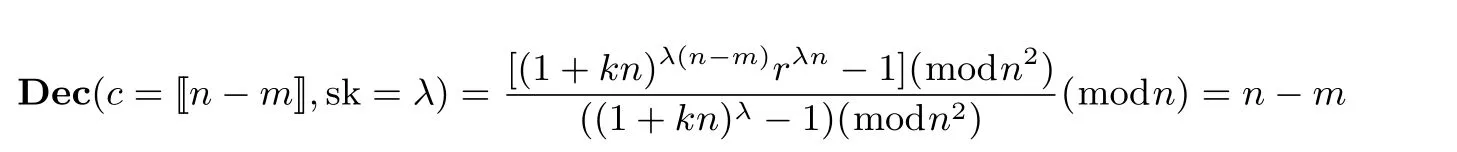
2.5 隐私保护的欧几里德距离计算协议



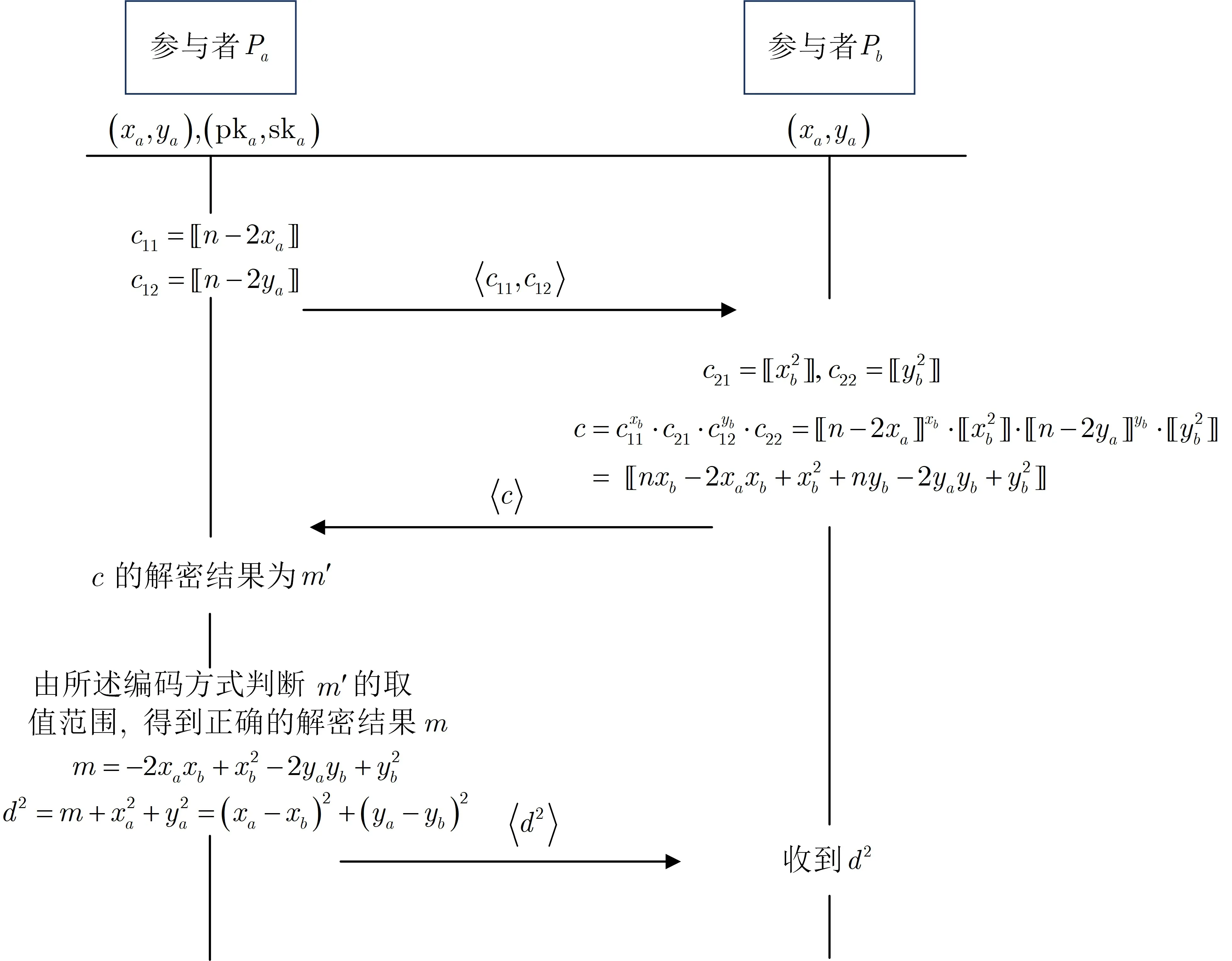
3 隐私保护的两圆间位置关系判定
3.1 问题描述

3.2 方案原理

3.3 具体方案
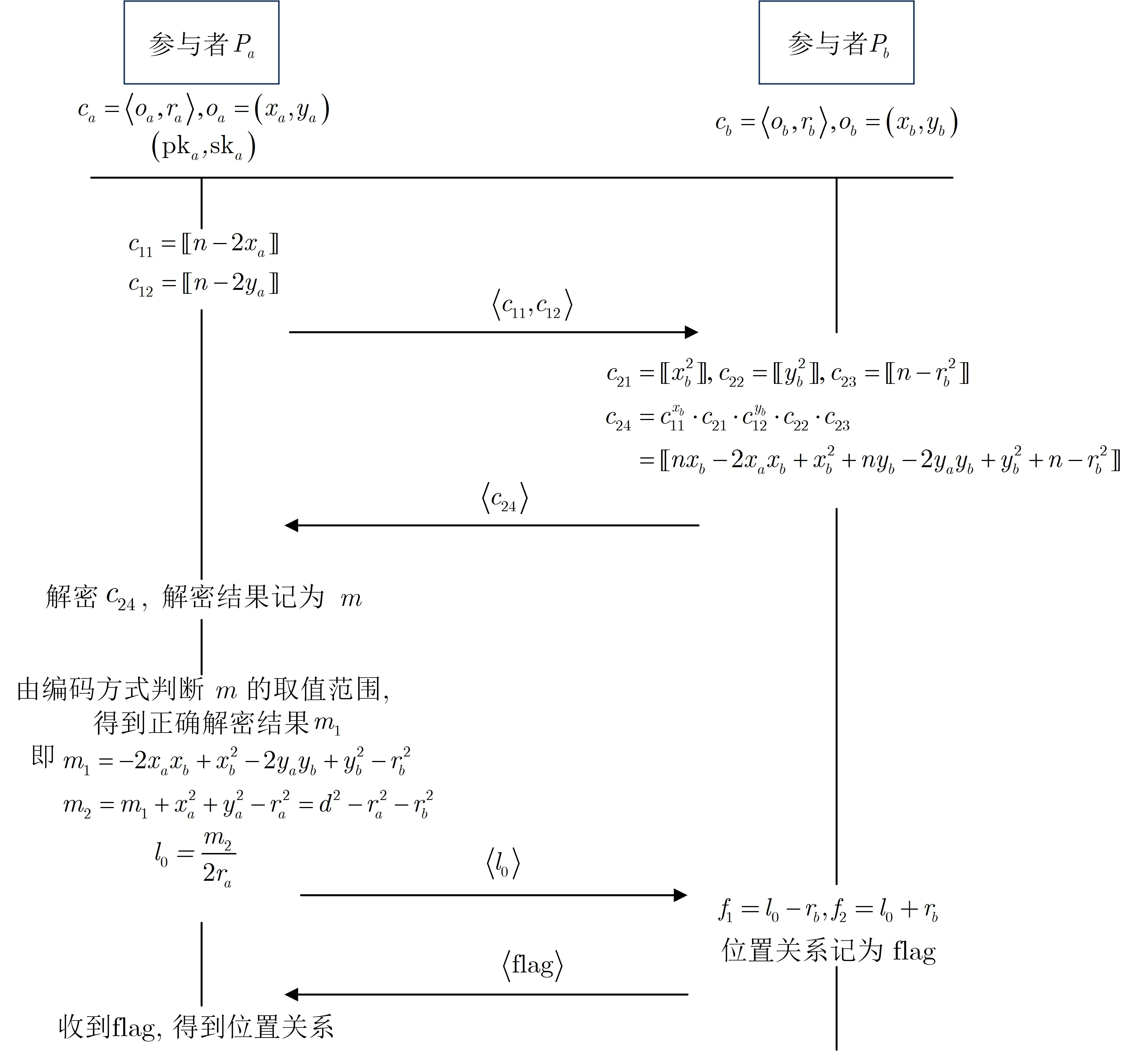

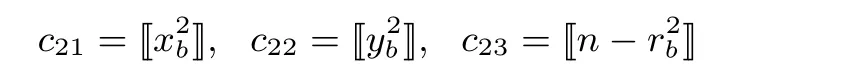
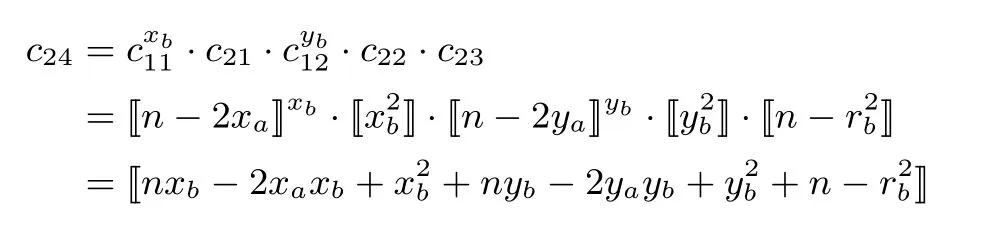

4 正确性及安全性
4.1 协议正确性分析


4.2 安全性分析

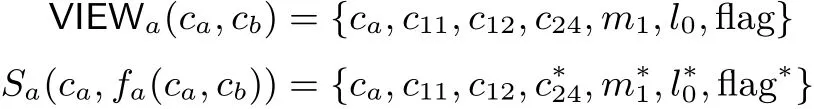
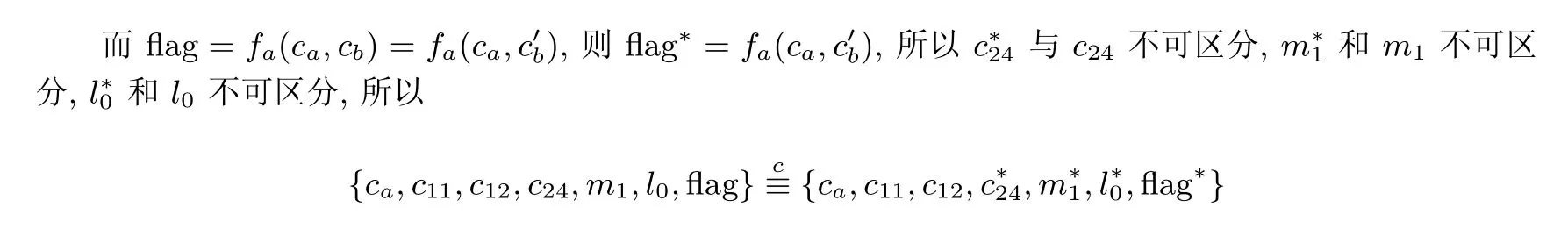


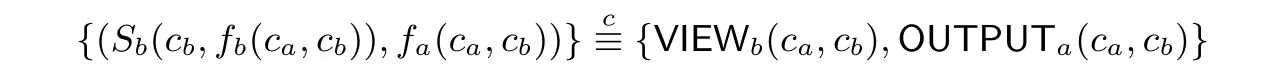
5 性能分析
6 结论
