命中位置对引爆重型爆炸反应装甲影响数值模拟
2021-03-19余庆波钟世威肖艳文赵宏伟
余庆波, 钟世威, 肖艳文, 赵宏伟
(1.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081; 2.陆军装备部装备项目管理中心,北京100072;3.火箭军研究院,北京 100094)
爆炸反应装甲可大幅度提升装甲车辆对破甲战斗部的防护能力,是目前反装甲弹药研发面临的主要技术挑战之一,也是国内外研究的热点方向. Held等[1-2]研究了射流与反应装甲靶板相互作用关系,并基于射流形成定常理论提出了定常侵彻模型. Z.Rosenberg等[3-4]采用数值模拟和实验相结合方法,研究了反应装甲对聚能射流的干扰破坏规律. Dejan Mickovic等[5]提出了聚能射流侵彻爆炸反应装甲的系列影响因素. 孙建军等[6]研究了反应装甲的干扰射流能力,并给出了最佳防护位置. 张雪朋等[7]采用静爆实验和理论分析相结合的方法,对活性射流作用反应装甲侵彻爆炸联合毁伤效应进行了研究. 李向荣等[8-9]提出了聚能射流打击主战坦克的毁伤评估方法,得到了射流临界侵彻深度. 以上研究更多采用实验方法研究反应装甲的防护能力,针对双层楔形反应装甲的引爆行为研究明显不足. 本文针对引爆问题,采用LS-DYNA进行数值模拟分析,重点研究命中位置对射流引爆重型反应装甲性能和飞板飞散及干扰时间等影响特性.
1 有限元建模
1.1 计算模型
目前,针对披挂反应装甲的装甲目标,通常采用两级串联破甲战斗部进行毁伤,前级小口径破甲战斗部用于引爆反应装甲,而后级大口径破甲战斗部用于毁伤装甲内部,本文主要研究前级战斗部对反应装甲引爆问题. 为此,数值模拟中采用小口径聚能战斗部,该战斗部主要由壳体、主装药和药型罩组成,战斗部口径为Ф48 mm,壳体为2 mm厚的45#钢,装药直径为Ф44 mm,装药选用8701炸药,装药高度为1.1倍装药口径,药型罩为锥角50°、壁厚为1 mm的紫铜药型罩,起爆方式为正起爆. 聚能战斗部结构示意图如图1所示.

图1 聚能战斗部计算模型Fig.1 Model of shape charge warhead
爆炸反应装甲模型主要由装甲盒、主装甲和上下两层“三明治”结构爆炸反应装甲组成,单层反应装甲结构如图2所示. 反应装甲外形尺寸为长320 mm、宽240 mm、高122 mm,主装甲为装甲钢,厚度18 mm,装甲盒厚度为3 mm,两层反应装甲之间的夹角为9°,飞板材料均为45#钢,厚度3 mm,装药均为PBX炸药,厚度为8 mm. 为观察装药爆炸情况,在反应装甲上下两层爆炸装甲装药内分别设置5个参考点,如图3所示. 计算采用流固耦合算法,其中,药型罩和空气域采用ALE算法,反应装甲采用拉格朗日算法,在ALE边界上设置流出边界条件. 另外,由于计算模型存在轴对称性,采用了1/2模型,计算模型采用前处理软件TrueGrid建立,并对模型进行3维网格划分,计算区域网格0.1 mm×0.1 mm×0.1 mm.

图2 单层反应装甲结构图Fig.2 Structure of the single ERA

图3 爆炸反应装甲计算模型及参考点设置Fig.3 Calculation model of ERA and reference points
1.2 材料模型
在本文数值模拟计算中,主装药采用JWL状态方程来描述.
(1)
式中:A,B,R1,R2,ω为炸药的材料参数;ν为爆表产物的相对比容;E为初始内能密度.
药型罩模型采用Steinberg材料模型和Gruneisen方程描述. Steinberg模型剪切模量为
(2)
式中:p为压力;v为比体积;Ec为冷压缩能量;Em为熔化能量;Ei为比热力学能;R′=Rρ/A;R为气体常数;ρ为密度;A为摩尔质量;G0、b、h、f为试验确定的材料参数. 屈服强度为
(3)
Gruneisen状态方程描述金属材料在高压下的状态特性. 由方程定义的压缩材料压力为
(γ0+αμ)E
(4)
式中:C为冲击波速度vS-vP曲线的截距;γ0为Gruneisen系数;a为修正系数,S1、S2、S3为vS-vP曲线斜率的系数.
飞板用Johnson-Cook模型和Gruneisen状态方程描述. Johnson-Cook模型的屈服强度为
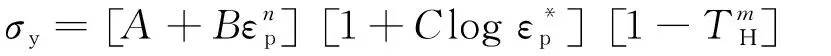
(5)
反应装甲夹层装药用Lee-Tarver点火增长模型描述. 该模型适用于炸药冲击起爆过程
G1(1-F)cFdPy+G2(1-F)eFfPz
(6)
式中:F为反应分数,它在模拟爆轰过程中控制着炸药化学能的释放;t为时间;ρ0为初始密度;ρ为当前密度;p为压力;I、G1、G2、b、x、a、c、d、y、e、g和z都是常数.
主装药主要参数列于表1,药型罩的计算模型主要参数列于表2,飞板基本材料参数列于表3,反应装甲夹层装药点火增长参数列于表4,材料参数来源于Autodyn材料库.

表1 主装药材料参数Tab.1 Material parameters of the main charge

表2 药型罩材料参数Tab.2 Material parameters of the liner

表3 飞板材料参数Tab.3 Material parameters of the flying board

表4 夹层装药点火增长参数Tab.4 The ignition and growth parameters of the explosive
聚能射流引爆爆炸反应装甲弹靶作用模型如图4所示,聚能射流形成方向与爆炸反应装甲法线方向呈58°角. 为了研究命中位置纵向和横向的移动对聚能射流侵彻爆炸反应装甲作用行为产生的影响. 选择有代表性的5个点,分别为靶板的中心点O,左1/4点A,左1/8点B,上1/4点C,左上1/4装甲中心点D,命中位置如图5所示,共5组工况.

图4 弹靶作用模型Fig.4 Model of projectile and targets
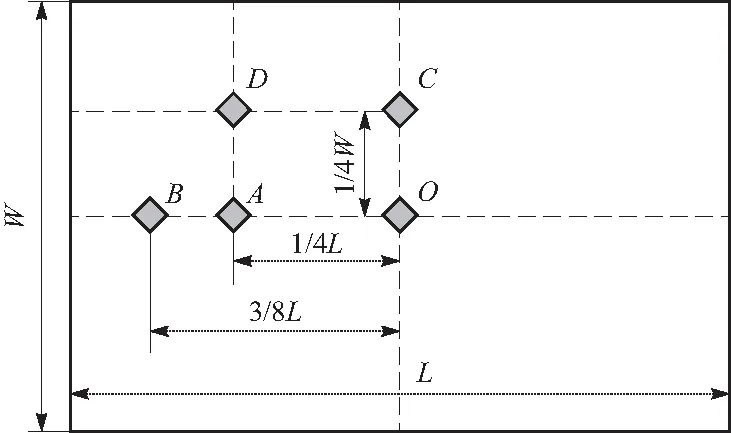
图5 装甲盒上命中位置(俯视图)Fig.5 Target position on the box(top view)
2 数值模拟结果及分析
2.1 侵爆性能分析
为了分析命中位置对爆炸反应装甲侵爆性能产生的影响,针对聚能射流对重型反应装甲的侵彻作用行为进行了数值模拟,典型数值模拟结果如图6所示. 命中位置是影响弹靶作用的关键因素,命中位置的改变会影响聚能射流的形态和完整性,进而影响射流头部速度及其侵彻性能,炸药层的爆轰特性也会随之改变. 从图中可以看出,随着命中位置从点O移动到点A,因射流穿透反应装甲主靶板后继续拉伸,射流形态变细变长,射流偏转角度增大,射流引爆上层装甲的位置更靠近装甲中心位置. 从上方观察,命中点O时,起爆位置更靠近飞板边缘,爆轰波到达飞板边缘的时间更短,稀疏波较快的进入炸药层中. 稀疏波的卸载作用降低了炸药爆轰波压力峰值和正压作用时间,缩短了炸药加速持续时间,降低了飞板的运动速度. 因此,命中点O时,飞板的变形程度小于点A;命中点C的变形程度小于点D.
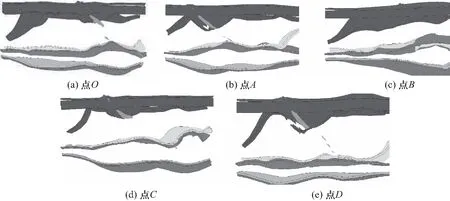
图6 不同命中位置的聚能射流对反应装甲的侵彻效应(450 μs)Fig.6 Penetration effect of shaped charge jets on reactive armor at different targets(450 μs)
从数值模拟结果看出,射流在引爆上层反应装甲后,受到反应装甲飞板的干扰作用,头部速度降低,出现颈缩断裂现象,连续性遭到破坏,失去继续侵彻和引爆下层反应装甲的能力. 但从压力曲线上看,下层反应装甲出现明显爆轰现象,由此得出,起爆原因是运动飞板的冲击效应. 运动飞板碰撞下层反应装甲,同时向炸药中传入冲击波将惰性装药起爆. 针对不同命中位置下的炸药引爆特性,选取炸药层中各5个参考点观察炸药,结果如图7所示.

图7 不同命中位置的炸药层引爆特性Fig.7 Detonation characteristics of explosive layers at different hit positions
由图7可知,在命中点为点O时,夹层装药的爆轰波峰值压力高于点A,正压作用时间没有明显变化. 在上层反应装甲炸药层中的5个观察点处,压力峰值大致相同没有发生衰减,正压作用时间约为40 μs. 根据压力脉冲到达相邻观测点的间隔时长,可以计算出爆轰波传播的平均速度,上层炸药的爆轰波速维持稳定、变化不大,说明上层炸药发生了稳定爆轰,爆轰波传播的速度约为7 800 m/s;靠近装甲边缘的观测点(6、7、10)出现了压力峰值降低以及正压作用时间延长的现象. 这说明了爆轰波在不断的衰减,波速降低至 2 000 m/s,在靠近装甲边缘处爆轰转为爆燃和燃烧. 下层反应装甲爆轰过程的强度显著低于上层反应装甲.
2.2 飞板飞散影响
针对命中位置变化对驱动飞板飞散的影响,选取双层楔形反应装甲的飞板,考察飞散特性随时间变化的趋势,图8和图9分别是命中位置不同的反应装甲各飞板飞散运动时速度-时间曲线和加速度-时间曲线.

图8 命中位置不同的反应装甲各飞板的速度-时间曲线Fig.8 Speed-time curve of each flying armor of the reaction armor with different hit positions
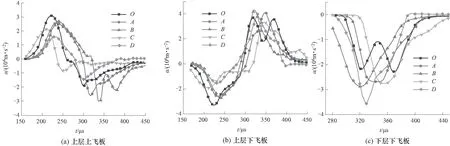
图9 命中位置不同的反应装甲各飞板加速度-时间曲线Fig.9 Acceleration-time curve of each flying armor of the reaction armor with different hit positions
从图9(a)中可看出,点O加速度的峰值为3.4×106m/s2,点A加速度的峰值为2.7×106m/s2,加速度峰值在命中位置沿x方向移动的过程,越靠近中心位置命中的工况飞板的加速度越大. 爆炸产生的冲击波传播到板边缘,会反射回一组稀疏卸载波,减弱爆轰产物的加载驱动现象. 点O较点A离飞板边缘更远,稀疏卸载波进入爆轰产物的时间变长,稀疏卸载作用减缓,因此点O的加速度峰值较点A更大. 同理,在沿y方向移动的过程中,点C加速度峰值较点O略小,是因为点C更靠近飞板自由表面,稀疏波进入变快.

图9 前级战斗部侵彻及飞板飞散示意图Fig.9 Front-level warhead and flying plates
命中位置影响飞板开始飞散运动的时刻和持续时间,由于上层反应装甲与主装甲之间存在一个夹角,命中位置影响射流侵彻装甲、引爆炸药所需的时间. 具体来说,命中点为点O的时间小于点A、B,点O的飞板开始运动的时刻较早,从图8(b)中可以看出,命中位置为点O、C的加速度峰值出现时间明显早于其他点,加速持续时间较短. 这是由于率先起爆装药驱动飞板沿外法线方向运动,撞击主靶板所需的时间更短,由于主装甲近似于静止状态,飞板加速度迅速减小至负值,加速阶段终止,进入塑性碰撞阶段.
而在命中位置沿x方向移动的过程,命中点更靠近中心的飞板速度更高,在y方向,命中点远离中心的飞板速度更高. 由运动学知识,在加载时间大致相当时,速度由加速度决定,因此飞板速度峰值随命中位置的分布规律与加速度的分布规律类似,越靠近中心位置越大.
2.3 干扰时间分析
干扰时间是反装甲两级串联战斗部设计的关键,干扰时间定义为射流起爆到引爆反应装甲的时间t1与飞板飞离射流流经区域的飞散时间t2之和. 为了分析反应装甲对串联战斗部的干扰时间飞板偏移出射流运动区域的时间,进而确定干扰时间,需要将飞板的飞散速度分解到坐标轴方向,如图10所示,飞板飞离方向为x方向和z方向. 飞离时间由最后飞离的飞板决定,此时爆炸反应装甲完全丧失对聚能射流的干扰能力,主战斗部起爆,直接打击主战坦克,对有生力量和武器装备造成有效杀伤.

图10 主战斗部侵彻及飞板速度分解示意图Fig.10 Main warhead and the speed of the flying plate
聚能射流的直径远远小于飞板的尺寸,在分析中可以忽略,射流流经的区域可用一条通过命中位置且方向与射流入射速度方向相同的直线等效替换,飞板边缘通过直线即视为飞离射流流经区域. 由表5可以得出,时间为450 μs时,各飞板加速度趋近于0,爆轰加载过程结束,飞板速度趋于稳定,忽略飞板速度衰减,将450 μs时刻的瞬时速度视为飞离流经区域的平均速度,命中位置为点O和点B的反应装甲飞板在450 μs时刻的速度分量列于表6.
由表6可知,命中位置为点O的工况下x方向飞离时间为29.04 ms,z方向飞离时间为38.5 ms,则干扰时间应为29.04 ms以上. 反应装甲起爆后,爆轰产物沿反应装甲飞板法线方向驱动飞板飞散,飞板主要是获得了x和y方向的速度,运动形式主要是以平动为主. 在飞板飞散的过程中,飞板受强大的冲击波作用产生了形变,飞板中心隆起,边缘出现弯曲,爆轰产物不再是平面加载,而是在变形的飞板表面进行曲面加载,运动形式变为平动与旋转的复合运动,飞板获得一个较小的z方向速度. 因此在点O,z方向的飞离时间更长. 各位置的干扰时间如表7所示.

表6 靶板450 μs时刻速度分量Tab.6 Velocity component of Target plates at 450 μs
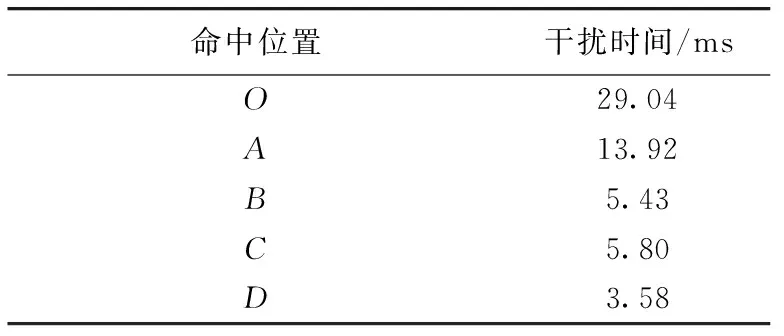
表7 不同命中位置下的干扰时间Tab.7 Interference time at different hit positions
由表7可知,命中位置的改变对干扰时间产生了较大的影响. 由图9可知,命中位置在x方向发生改变时,越接近中心位置,在上层反应装甲的起爆点逐渐向上移动,飞板飞离时间t2增加,干扰时间延长. 而命中位置在z方向发生改变时,越靠近装甲边缘,飞板飞离射流流经区域的时间t2越短. 因此,更靠近边缘的点C干扰时间比点O短.
3 结 论
采用LS-DYNA非线性动力学软件针对命中位置对引爆重型爆炸反应装甲影响进行了数值模拟,主要结论如下.
① 命中位置影响爆轰波到达自由表面的时间和稀疏波进入炸药层的时间,炸药加速持续时间和加速度都会变化,炸药爆轰波压力峰值和正压作用时间随命中位置改变而发生改变.
② 命中位置的变化会使飞板获得的加速度、速度峰值变化,越靠近装甲边缘,峰值越小,且飞板边缘区域出现翘起扭曲等现象,影响飞板的整体速度方向,飞板的旋转运动更加明显.
③ 命中位置影响反应装甲干扰时间,通过速度分量图得出了飞板的飞离时间,飞离时间由命中位置离边缘的距离决定,确定了在不同命中位置处反应装甲对聚能射流的干扰时间.
