一种子目标和水平集方法融合的AUV动态航路规划新算法

盛亮， 苏宁， 罗荣， 冯炜

(1.海军航空大学 航空基础学院，山东，烟台 264001； 2.锦西工业学校，辽宁，葫芦岛 125001；3.海军研究院，北京 102442)

自主水下潜航器(autonomous underwater vehicle，AUV)在复杂的海洋环境中航行时，一是事先不可能预知航路范围内的所有固定障碍物和威胁区；二是突发的移动障碍物，比如大型鱼类、鱼群、其他水下潜航器等也可能出现在预先规划好的航路上；三是预先规划的全局航路上也可能会遇到时空变化剧烈的海流. 以上这些情况都会危及AUV的航行安全，故其必须具备良好的自主实时避障、避险航路规划能力. 基于此，众多学者开展了AUV实时避障航路规划方法的研究.

文献[1-10]中开展了水下潜航器的实时避障航路规划研究，如进化计算[1]、遗传算法[2]、粒子群算法[3-4]、蚁群[5]、人工势场法[6,7]、几何方法[8]、生物启发方法[9]以及启发式搜索的D*Lite算法[10]等，仿真表明这些算法都能够有效地规避未知的静止障碍物和突发运动障碍物，但这些算法都存在一个明显的先天不足之处：未知障碍物建模为圆形或球形，且假定圆心或球心和半径可由传感器获得的信息直接得出. 而在实际航行中，AUV很难获得障碍物的具体尺寸和中心位置. 文献[11-13]中基于虚拟子目标的思想研究了机器人的避障路径规划，原理清晰、简单，实现方便. 此外，从AUV实时避障航路规划的众多研究中可知，绝大多数的实时避障研究仍在二维平面内进行，少量的三维空间避障规划也是将空间分成了水平面和垂直面进行规划，理论基础仍是二维平面内的实时避障航路规划. 因此，当前AUV自主实时避障航路规划的研究重点仍在二维平面内的航路规划上.

本文将这种思想融入到水平集算法之中，基于AUV的前视声呐探测的障碍物情形，预估障碍物尺寸和中心位置，据此得出安全可靠的子目标点，提出了一种基于子目标法和水平集方法[14]的二维自主实时航路规划新算法. 新算法能确保建立更为符合实际的避障航路，且在完全避障的情况下，尽可能利用海流航行至终点.

1 基于AUV前视声呐探测的障碍物模型

1.1 前视声呐探测模型

AUV用于避障探测的传感器主要是前视声呐，其获取的实时信息为其自主实时避障航路规划提供依据. 本文以某型水下AUV搭载的前视声呐为例进行说明. 图1是其探测区域示意图，它是一种多波束的主动型声呐，通常安装在水下潜航器的前端，通过发射多束声波对前方环境进行水平和垂直扫描探测，图中所示水平探测角度范围为[-αso/2,αso/2]，垂直探测范围[-βso/2,βso/2]. 若前方有障碍物且在声呐探测范围内时，反射回的声波被声呐接收处理生成原始的声呐图像，再通过相应的图像处理和特征提取算法得到栅格化的轮廓边缘. 通过反射回的声波还可以得到AUV到障碍物边缘的距离以及相应的方位. 以上述获取的信息为基础，即可开展后续的自主实时避碰航路规划[15]. 本文不涉及图像处理和特征提取研究，故而假定通过声呐探测已直接获取了栅格化的障碍物轮廓.

图1 AUV前视声呐探测范围Fig.1 The detection range of AUV’s forward-looking sonar

海洋环境中，AUV在遇到障碍物时，不考虑转弯角限制，可在AUV前方的三维空间众多方向上实施机动避障，若进行航路规划时都考虑到，算法将极为复杂，且规划效率低. 因而，本文将声呐探测、障碍物建模及自主实时避障航路规划均限定在水平面内. 故而，前视声呐的探测范围可以表示为图2形式. 其中，Rso为其有效的最大探测半径，[-αso/2,αso/2]仍为其角度探测范围.

图2 前视声呐二维探测范围模型Fig.2 The 2D model of detection range of AUV’s forward-looking sonar

1.2 未知固定障碍物模型

AUV沿着全局最优航路航行过程中，前视声呐在探测到未知的固定障碍物时，并不能完全获知障碍物的尺寸和中心位置，仅能够探测到障碍物的部分边缘位置及其距离AUV的距离，如图3所示. 将未知固定障碍物限定为凸集，非凸集的部分用补缺的方法转换为凸集[16]，进而采用凸集的外切圆对障碍物建模.

图3 声呐探测的障碍物边缘Fig.3 The edges of the obstacle detected by sonar

设某时刻t时，AUV在其预定的航向上发现有障碍物，此时，可探测到的障碍物边缘与AUV及其声呐的探测范围如图4所示3种相对位置关系.

图4 声呐探测区与障碍物位置关系Fig.4 The relationship between sonar detection area and obstacle position

图4(a)中，声呐发出的声波无法探测到障碍物的边缘，而在未知障碍物边缘的情况下，无法基于此时的局部障碍物边缘信息进行建模并航路规划，因此，AUV应减速，并判断两侧以最大探测角发出的声波线与障碍物相交的点Q1和Q2哪个离AUV距离更远，图中所示为右侧Q2点. AUV为确保更高的安全性，减速航行的同时向更远点Q2方向逐步转向，每一步的转向角设为Δαso，转向直至发出的最大探测角的声波线与障碍物边缘相切，记下此时的点Q′2. 构建外切圆形障碍物模型时将以点Q1和点Q′2为基准. 图4(b)中，声呐发出的声波探测到了障碍物的某一侧(右侧)边缘，与障碍物相交于点Q4. 此时构建外切圆形障碍物模型时将以点Q3和点Q4为基准. 图4(c)中，声呐发出的声波探测到障碍物的所有边缘，分别与障碍物相交于点Q5和点Q6. 故此时构建外切圆形障碍物模型时将以点Q3和点Q4为基准.

不失一般性，以图4(b)中情形为例进行建模，图4(a)和图4(c)中情形在建模时方法一样. 在图4(b)中，由于能探测到障碍物的右侧边缘，故可认为右侧信息较左侧更完备，障碍物建模的可信度更高，因此航路规划时选择右侧通过安全性更高，因而下一步子目标点选择时选择从障碍物模型右侧选点. 基于点Q3和点Q4为基准的圆形障碍物建模如图5所示.

图5 基于探测基准点的圆形障碍物模型Fig.5 The circular obstacle model based on detection datum point

则中心点Q7坐标可表示为

由三角函数公式可知点Q3和点Q4间距离为

(1)

另可得∠OlmsQ4Q3为

(2)

易知∠OlmsQ4Q3=∠O4QobQ7,故

(3)

故而，Q4Oob距离为

(4)

则障碍物模型的圆心在AUV随体坐标系下的坐标为：(d1，d4). 圆的半径为：r=d4. 航路规划时，通常将AUV当做一个质点，因而，障碍物建模时通常按照AUV的尺寸进行膨胀处理，亦即最后得到的障碍物模型为圆心在坐标(d1，d4)处，半径为r=d4+l0，式中l0为AUV的长度.

对于图4(a)中的障碍物情形，以点Q1和点Q′2为基准，完全参照上述方法建模；对于图4(c)中的障碍物情形，选择从距离AUV较远的交点Q6侧绕行，故以该点作为外切点对障碍物建模，方法不变.

1.3 突发移动障碍物模型

海洋环境下，突发的移动障碍物的尺寸和圆心建模，参照未知固定障碍物的建模思路进行. 除此之外，由于移动障碍物具备一定的速度，且方向和大小往往是随机的，在上述模型的基础上需要加上动态不确定性.

海洋中的突发移动障碍物主要是指鱼类、鱼群、AUV平台或潜艇等，它们在水下运动的过程中有较大的随机性，因而本文将突发的移动障碍物模型统一设定为一个随机的离散时间系统[17]，即

(5)

式中Wi为障碍物的状态表示，代表了障碍物位置、速度及随机性. 可进一步表示为

Wi=[WpWvWυ]T

式中：Wp=[WpxWpy]为障碍物圆心的期望坐标；Wυ表示障碍物圆心坐标的不确定性，其随不确定性参数dυ的变化而变化；Wv=[WvxWvy]为障碍物的运动速度，表示对地速度，由海流速度和自身速度合成；障碍物的随机性运动由Ui -1表示，代表一个叠加在障碍物速度上的随机扰动，其服从正态分布：Ui -1～N(0,σ2). 模型化后，突发移动障碍物的状态可表示为

(6)

方程组可变为矩阵形式

Wi=G0Wi -1+U0Ui -1+I0dυ

(7)

式中：

突发移动障碍物模型的仿真见图6所示.

图6 海流环境中的突发移动障碍物模型Fig.6 The model of sudden moving obstacle in current environment

从图6中可以看出，障碍物模型包含了原来的圆形模型和新加入的运动因素和随机因素，建成了一种用于自主实时避障航路规划的近似话筒型的移动障碍物模型.

2 基于子目标法和水平集方法的自主实时航路规划算法

AUV在自主航行过程中，因受到水下声波探测距离的限制，能够获取的环境信息有限，为确保避障成功和航行安全，每一次自主实时航路规划都是规划空间较小的局部航路规划. 因而，需要在每次探测到航向上存在障碍物或可能与障碍物交会的情况下，在局部规划空间中设定一个合适的子目标点以取代预先规划的下一航路点，再利用水平集方法快速规划出能够到达子目标点且确保能避开障碍物、充分利用海流的局部最优航路.

2.1 子目标点的选取

对于未知固定障碍物和突发移动障碍物，子目标的选取方法有所不同，下面分开进行说明.

2.1.1遭遇未知固定障碍物时子目标点的选取

遭遇未知固定障碍物时，不失一般性，以图5所示模型为基础进行选取. 此时，选取方式如图7所示.

图7 未知固定障碍物时的子目标点Fig. 7 Sub-target for unknown fixed obstacle

子目标点选取的过程如下：先将图5中的障碍物圆形模型进行膨胀处理，膨胀后圆心位置不变，半径增加AUV的自身长度，即l0，形成膨胀后的障碍物圆形模型，即图7中大网格状圆表示区域. 在实施自主实时航路规划过程中，大网格圆区域将作为规划空间中的禁航区一直存在. 沿着半径增加的方向OobQ4继续延伸l0长度到达一点Q8，此点即为当前选定的子目标点. 可求出子目标点的坐标为：(d1，2l0).

2.1.2遭遇突发移动障碍物时子目标点的选取

突发移动障碍物出现在AUV预计的航路上或可能在预计航路上交会时，将会出现障碍物向AUV预计航路的左方移动、障碍物向AUV预计航路的右方移动、障碍物在AUV预计航路上与其相向运动或在预计航路上与其同向运动且速度小于AUV的速度等4种情形.

① 障碍物向AUV预计航路的左方移动.

此种情形下有可能会与AUV在其预定的航道上相遇. 为了确保完全避障，需要规划出一条局部优化避障航路. 可在初次探测到障碍物所在位置的右方选取子目标点Q9，如图8所示. 此时，AUV应向预计航路的右侧转弯航行.

图8 障碍物向AUV预计航路的左方移动Fig.8 The moving obstacle to the left of the AUV’s intended course

② 障碍物向AUV预计航路的右方移动.

此种情形子目标点的选择方法与图8中类似，应在初次探测到障碍物所在位置的左方选取子目标点.

③ 障碍物在AUV预计航路上且两者相向运动.

此种情形碰撞威胁的风险较高，需要以较大的转弯角进行改航回避，且此时应尽可能先降低航行速度. 子目标通常选择第二次探测到障碍物时的最近点左方或右方垂直距离2l0处，如图9中的Q10点所示.

图9 障碍物在AUV预计航路上且两者相向运动Fig.9 The moving obstacle on the predicted route of AUV and in opposite direction

④ 障碍物在AUV预计航路上且两者同向运动.

此种情形下若障碍物的速度高于AUV的速度，则不用考虑避障规划问题，AUV可以完全按照预计航路航行；若障碍物的速度低于AUV的速度，AUV有可能在预计的这段航路上追上障碍物，因而需要开展避障规划，此时子目标点选择方法如图10所示.

图10 障碍物在AUV预计航路上且两者同向运动Fig.10 The moving obstacle on the predicted route of AUV and in same direction

在图9中点Q10选取的是在预计航路的左侧，与第二次探测到障碍物时的最近点相距l0，且两者的连线与预计航向垂直. AUV到达点Q10后再次进行判断前方航路上与障碍物交会的可能性，此时的情形类同于本小节①中图8的情形，继续进行子目标点的选取和航路规划；若无交会的可能，则按照自主实时规划的局部航路航行至终点.

2.2 水平集方法

考虑海流影响，将水平集方法用于AUV的航路规划时[10]，设海流速度为v(X,t)，AUV的运动由0水平集的运动决定，水平集演化方程中的演化速度则由海流速度和AUV自身速度合成，演化方程为

由式(8)生成模拟海流

(8)

式中：vx(r)，vy(r)分别为水平和纵向方向的涡流速度分量；κ、ξ分别用来描述涡流强度、涡流半径坐标；ri为第i个涡流中心的位置，仿真中，涡流中心位置随机生成，n为叠加的涡流个数；vcx，vcy分别为定常流vc在水平、纵向方向的速度分量.

初始条件为：φ(X,0)=|X-Ys|，Ys为AUV的初始位置. 其中，FAUV(X,t)为AUV自身速度，亦即AUV相对海流的速度. 为保证所求路径为时间最优，要求FAUV(X,t)的方向为水平集函数的梯度方向，则式(8)可进一步化为如下Hamilton-Jacobi方程，亦即基于水平集方法的AUV航路规划演化方程

(9)

当AUV航行至终点附近时，终点落在了0水平集内. 通过式(10)进行回溯求解，即得最优航路. 回溯方程为

(10)

2.3 算法步骤

基于子目标法和水平集方法的自主实时航路规划算法包含针对未知固定障碍物的算法和针对突发移动障碍物的算法两部分，现给出遭遇未知固定障碍物时算法步骤.

① 初始化规划空间为二维栅格笛卡尔空间，初始化AUV速度、起始点和终点坐标，初始化已知固定障碍物和威胁区. 设定演化参数和AUV速度，按式(8)初始化模拟海流场.

② 依照水平集方法规划出当前海洋环境下的最优航路，并按照该航路开始航行并启动前视声呐探测.

③ 声呐探测发现当前航向上存在未知固定障碍物，按照1.2中的方法对障碍物进行建模并处理成禁航区；按照2.1.1中的方法选取子目标点Qi，记录下当前点位置和子目标点位置.

④ 依照水平集方法从当前位置点和刚刚选取的子目标点Qi间以及该子目标点Qi和终点间规划出两条优化航路i和′i，然后沿航路i航行至点Qi，在点Qi处开启声呐探测，当探测到航路′i的当前航向上仍然存在障碍物时，i++，转③；若无障碍物，则沿航路′i向终点航行，将此时探测到的未在航路上的障碍物边缘按1.2中的方法进行建模并处理成禁航区后与先前的禁航区合并.

其算法流程图如图11所示.

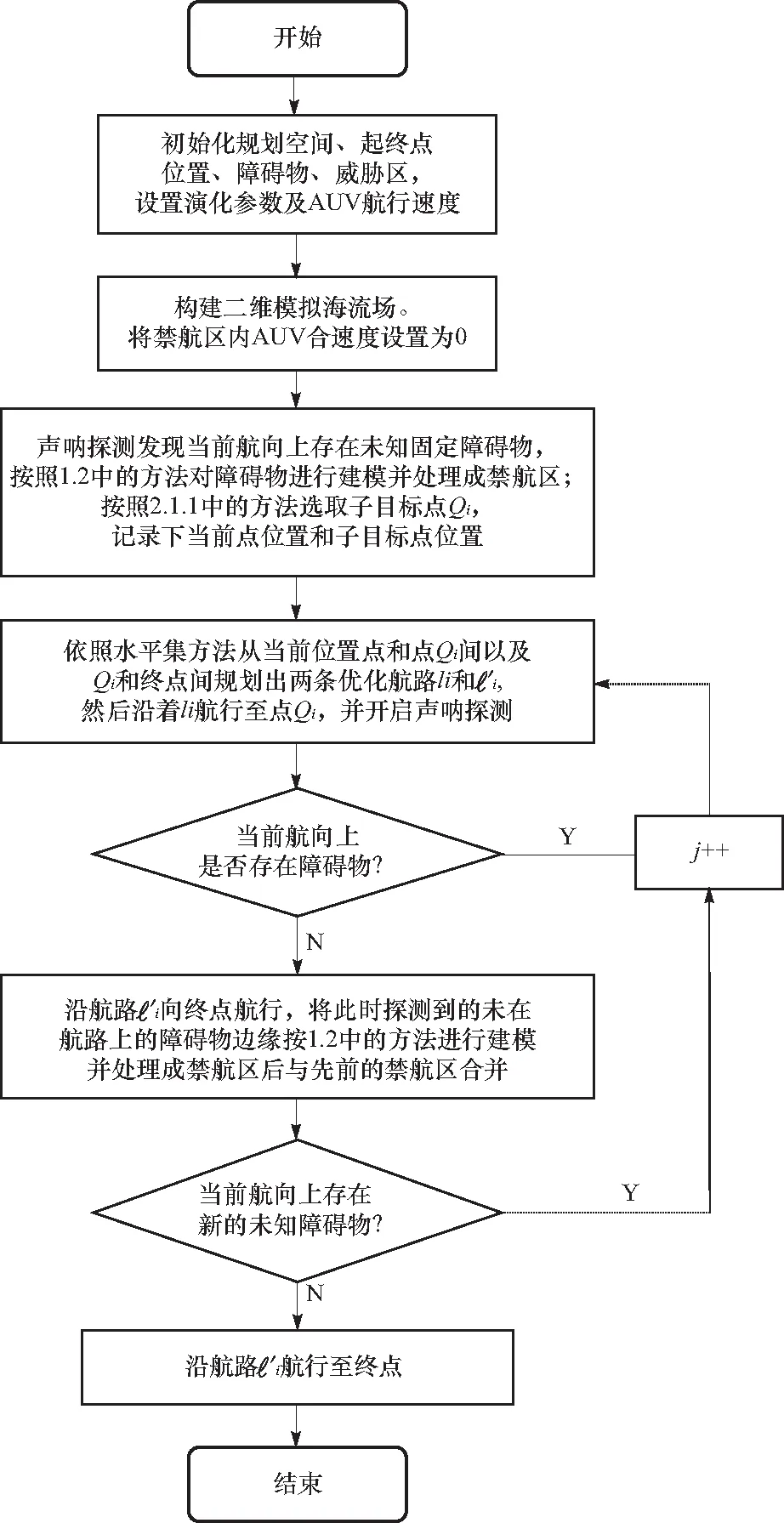
图11 遭遇未知固定障碍物时自主实时航路规划混合算法Fig.11 Hybrid algorithm for autonomous real-time route planning when encountering unknown fixed obstacles

遭遇突发移动障碍物时的算法步骤与遭遇未知固定障碍物时的算法步骤类似，其算法流程图如下图12所示.

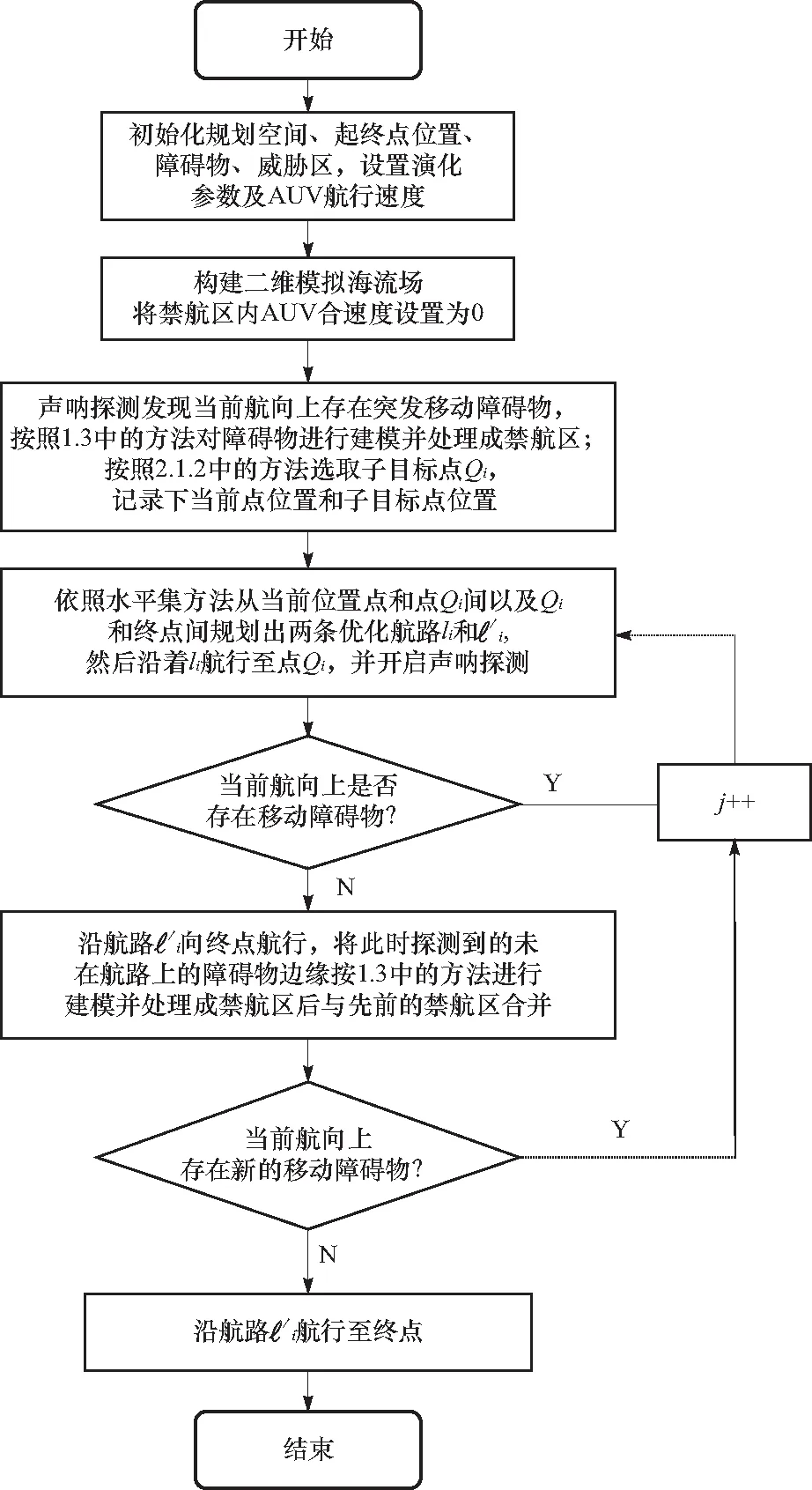
图12 遭遇突发移动障碍物时自主实时航路规划混合算法Fig.12 Hybrid algorithm for autonomous real-time route planning when encountering sudden moving obstacles

3 案例仿真与结果分析

本节对新算法开展仿真研究，验证模型和算法的可靠性和有效性.

3.1 案例一：未知固定障碍物情形

未知固定障碍物环境下，设定规划空间为1 000 m×1 000 m的二维笛卡尔坐标空间. 栅格间距为1 m. 起始点坐标为(10，35)，终点坐标为(90，70). 真实海流的模拟由5个随机涡流和斜向右上方的定常流叠加而成. 已知障碍物与威胁区的设置：2个敌对探测威胁区域分别为：威胁1圆心坐标(350,500)，威胁半径为5.5 m. 威胁2圆心坐标(650,400)，威胁半径7 m. 2个障碍物建模为5边形模型，障碍物1的5个顶点坐标为：(510,760)，(460,742)，(471,620)，(563,620)，(572,729)；障碍物2的5个顶点坐标为：(399,351)，(370,340)，(361,272)，(430,258)，(430,340). 算法首先基于已知的障碍物和威胁区通过水平集航路规划方法生成一条全局最优航路，即图13中所示虚线所示航路.

图13 遭遇未知固定障碍物时的航路规划仿真Fig.13 Simulation of route planning when encountering unknown fixed obstacles

AUV先沿着规划的虚线所示航路潜行，至6角星点处，前视声呐探测到有未知的固定障碍物，则启动障碍物建模和子目标点选取，依据探测到的障碍物边缘信息建立的模型即图中的“+”号边缘圆，子目标点即为米字点所在位置，坐标为(698.972,791.523). 在AUV当前点(6角星点)和子目标点(米字点)、子目标点和终点之间分别进行最优航路规划，所得即为图中实线表示的拼接后的航路. 从图14中可知，AUV能够在充分利用海流的情况下，安全避开障碍物航行至终点. 此外，整个自主实时航路规划仅取了一个子目标点就实现了至终点的避碰航路规划.

图14 障碍物向预计航路的左方移动时航路规划仿真Fig.14 Simulation of route planning when obstacles move to the left of the predicted route

预先规划的全局最优航路和自主实时规划后的实际航路数据如表1所示.

从表1可知，避障规划后，实际航行长度较预先规划的航路要长2.32%，航行时间要长2.06%. 增加值很小，因此，2.3.1节中提出的针对未知固定障碍物的避障混合算法不仅能够完全避障，而且避障后规划的航路仍然是最优的. 算法的可靠性和有效性得到了验证.

表1 两种航路性能对比Tab.1 Performance comparison of two routes

3.2 案例二：突发移动障碍物情形

突发障碍物情形是在案例一规划空间基础上加入未知的移动障碍物，这些障碍物的位置具有不确定性. 按照1.3节的方式对移动障碍物建模. 障碍物速度分布在-3 m/s和3 m/s之间，方向由速度分量的不同所决定，位置的不确定性随时间的增长而线性增加，为简化分析，假定从声呐探测到障碍物到AUV安全完成避障的整个过程中障碍物的移动方向大致上不变. 图14～图17分别为4种情形下的避障航路规划仿真示意图.

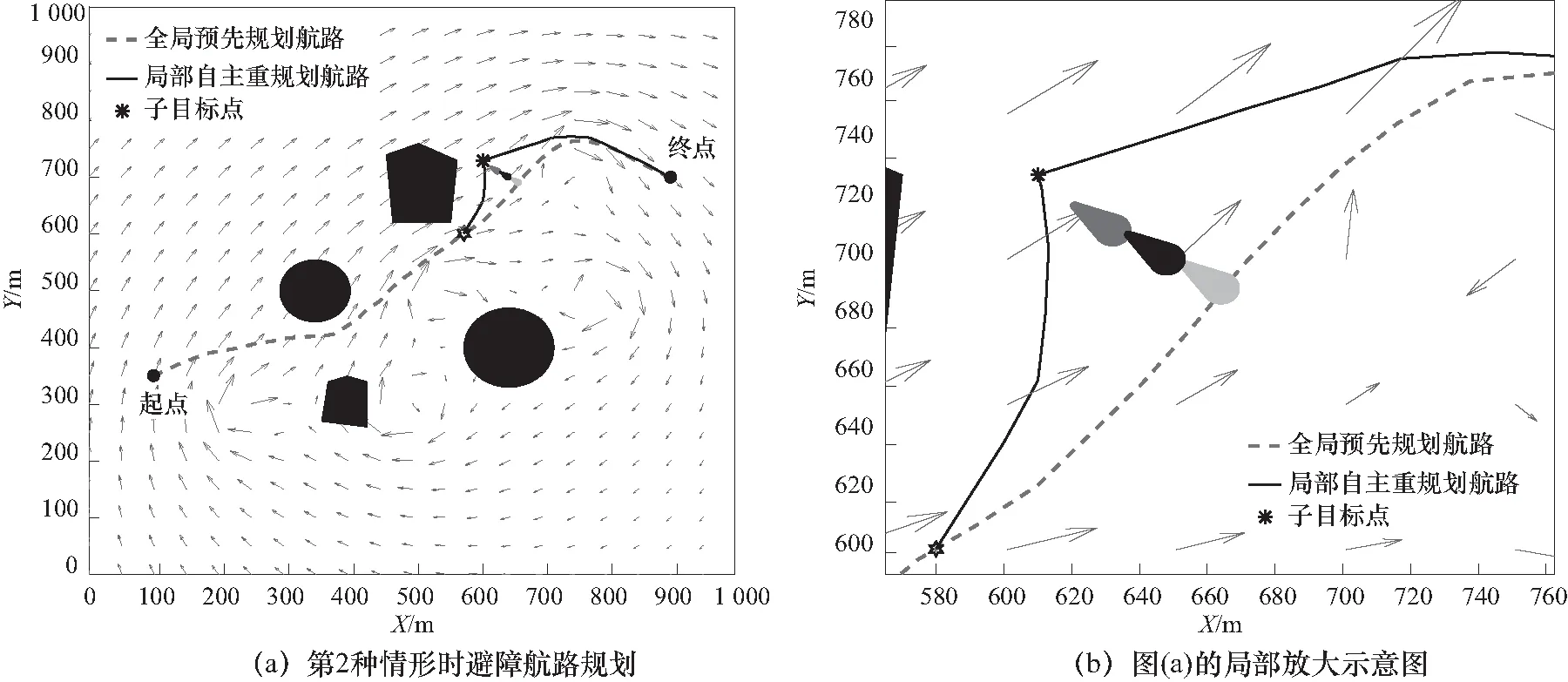
图15 障碍物向预计航路的右方移动时航路规划仿真Fig.15 Simulation of route planning when obstacles move to the right of the predicted route

图16 障碍物在预计航路上且相向运动时航路规划仿真Fig.16 Simulation of route planning when obstacles move in opposite direction on the predicted route

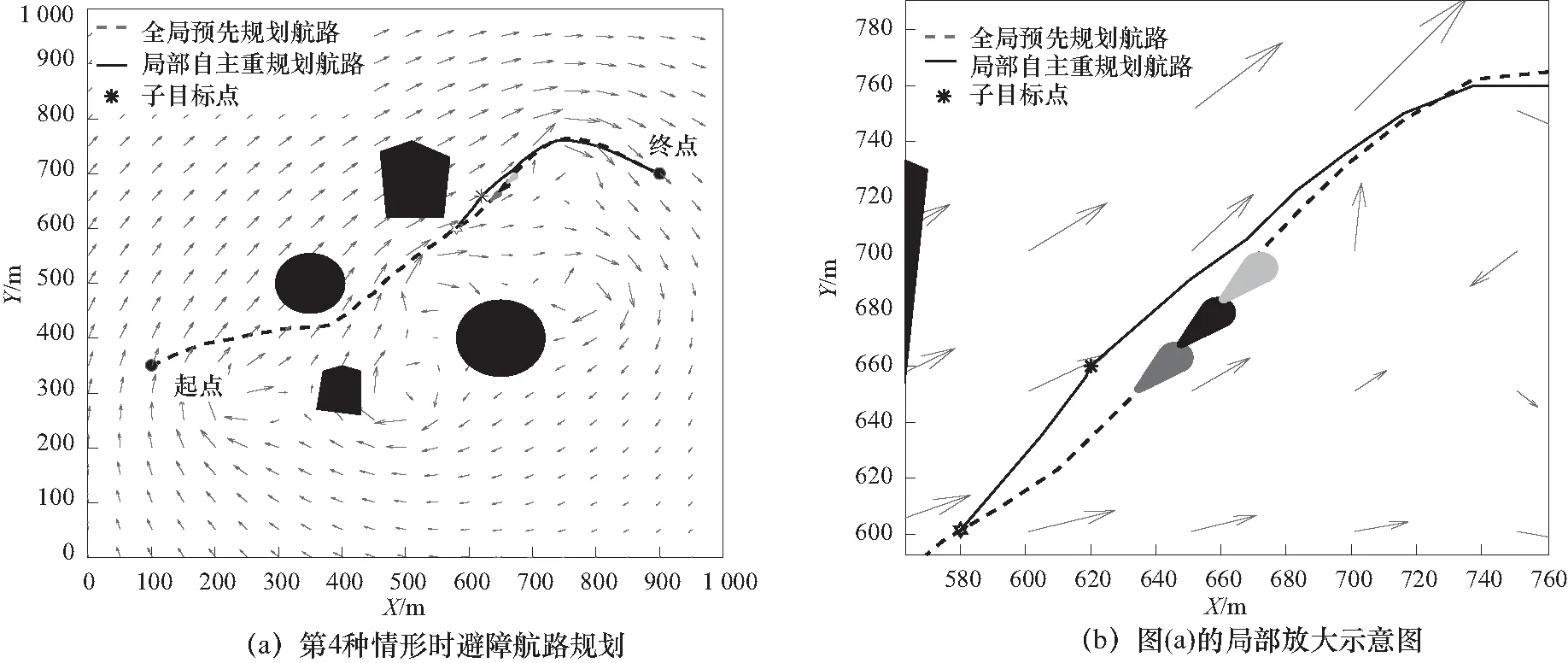
图17 障碍物在预计航路上且相向运动时航路规划仿真Fig.17 Simulation of route planning when obstacles move in same direction on the predicted route

显然，从图14～图17中易知，4种情形下采用图12中的算法进行自主实时避障航路规划是完全成功的. 预先规划的全局最优航路和4种情形下自主实时规划后的AUV实际航路取平均后得到数据如表2所示.

表2 两种航路性能对比Tab.2 Performance comparison of two routes

从表2易知，避障规划后，实际平均航行长度较预先规划的航路要长1.87%，航行时间要长4.77%. 航路长度增加值很小，但航行时间增加值稍有些大，主要原因在于为了成功避开移动的障碍物，自主实时规划的航路上海流所起的正作用不如全局预先规划航路上的海流正作用大. 总体而言，在保证100%规避突发移动障碍物的情况下，本文算法规划的自主实时航路的性能较原来的全局最优航路的性能下降量很小，说明本文算法规划的航路是可靠和有效的，算法是符合实际要求的.

4 结 论

由于水下环境的不可完全预知，故本文针对海洋环境中的未知固定障碍物和突发移动障碍物开展了AUV的自主实时避障航路规划技术研究. 在AUV前视声呐探测模型的基础上，分别对未知固定障碍物和突发移动障碍物进行了建模，提出了2类较为符合实际的二维障碍物模型；在2类模型的基础上，进一步研究了航路规划中子目标点的选取方法. 针对未知固定障碍物，提出了一种基于外切膨胀障碍物圆的子目标点选取方法；针对突发的移动障碍物，基于其运动方向与AUV预计的航向的关系，给出了4种不同的选取子目标点的方法. 最后结合子目标点法和水平集方法，对未知固定障碍物和移动障碍物中的4种运动情形进行了自主实时避障航路规划，仿真结果表明，本文提出的算法均能做到完全的避障，且避障后的航路性能质量较原来全局最优航路的性能质量下降得很小.