海上养殖平台系泊系统耦合动力分析

2021-03-19张晓莹林国珍李晓文

船舶与海洋工程 2021年1期

张晓莹，扈喆，林国珍，李妍，李晓文

（集美大学 a.轮机工程学院；b.福建省船舶与海洋工程重点实验室，福建厦门 361021）

0 引言

近年来，随着人们开发利用海洋生物资源的步伐逐步加快，各种海上养殖平台设计概念不断出现。由于海上养殖平台通常需在海洋中长期作业，因此保证其具有良好的水动力性能和系泊系统的安全性至关重要。相比船舶和石油平台等常规海洋结构物，海上养殖平台设计灵活、形式多样，目前尚无统一完善的标准或规范可循。对于具体的设计方案而言，应根据海上养殖平台的结构形式特点，采用合适的理论和技术手段评估其水动力性能和系泊系统安全性。

目前工程上主要采用三维势流理论评估水动力性能，例如：杨子恒等基于SESAM软件分析预报了某远洋渔船的波浪载荷；雷林等采用AQWA软件计算了某多体浮式消波堤的附加质量；周叶等基于RANKINE源法建立了近岛礁浮体水动力性能直接分析耦合模型，分析了考虑近岛礁海底地形之后浮式平台的运动和载荷响应特性；孙建群等基于三维频域势流理论分析了某多模块浮桥的水动力性能，并进行了试验对比。在平台-系泊系统耦合动力学分析方面：冯亮等采用Orcaflex软件，通过时域耦合动力分析的方法计算了某波浪能发电平台系泊缆的动张力响应；MA等采用异步耦合算法计算了某浮式平台-锚泊系统的耦合动力响应；SUN等研究了波流共同作用下某多杆型平台与其系泊系统的时域耦合动力响应。

本文以某浮式管架结构养殖平台为例，采用SESAM软件计算其水动力性能和在随机海况下的平台-系泊系统耦合动力响应；同时，分析平台运动幅频响应特性、锚链载荷谱、波频振荡与二阶力特性、最大锚链拉力变化和平台运动规律等，为类似平台的设计和安全性评估提供参考。

1 基本参数

该平台为浮式管架结构，总长71m，作业水深40m，立柱直径2m，间距10m，高度5m。系泊系统采用四角辐射形式，3 根锚链为1 组，共4 组锚链。选取AR3 级D60 有档锚链，单根长度为240m，在静水中的触底长度为140m，破断强度为3147kN，重78.84kg/m。平台与系泊系统布置示意见图1，其中坐标系原点定在平台中心处，高度与静水面持平，x 轴为平台长度方向。

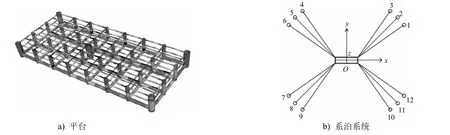
图1 平台与系泊系统布置示意

2 基本理论

由于平台是由小尺度构件组成的，故采用Morison公式进行水动力分析，有

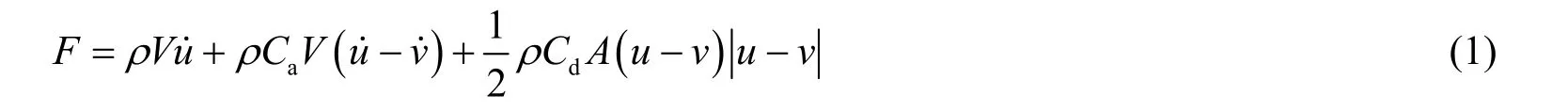
式(1)中：ρ 为流体密度；V 为杆微元体积；u 和u˙分别为流体速度和加速度；v 和v˙分别为杆微元速度和加速度； C为附加质量系数； C为阻力（拖曳力）系数。等式右端第1项为Froude-Krylov力，第2项为水动力惯性力，第3项为阻力（拖曳力）。对于圆柱形管件，取 C=1 。规范建议阻力系数 C的取值范围为0.6～1.2，实际取值多考虑雷诺数Re的影响，文献[10]建议采用表1计算阻力系数。本文所述平台管件雷诺数Re大于5.0×10，故取 C=0.7。

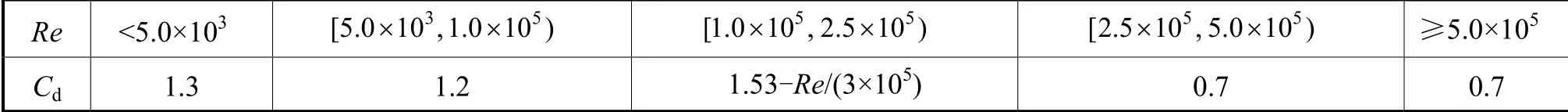
表1 阻力系数取值随雷诺数Re变化

将Morison公式线性化之后得到平台六自由度运动方程为

式(2)中：M 和M分别为质量矩阵和附加质量矩阵；C 为黏性阻尼矩阵；K 为静水回复力矩阵；K为系泊系统的附加刚度矩阵；F 为外界激励；X 为平台六自由度运动位移。一般系泊系统具有非线性特性，但在对平台主体进行水动力分析时，采用准静态方法将系泊系统线性化。

得到平台水动力系数之后，采用时域方法求解平台-系泊系统的耦合动力学方程，并采用有限元法计算系泊缆的强度。以上计算分别在SESAM.HydroD模块和SESAM.DeepC模块中进行。

3 平台水动力计算结果

建立平台主体水动力模型，该模型由4243个梁单元组成，节点数为3259个。根据平台实际重量分布建立平台质量模型，该模型由18240个梁单元和6334个板单元组成，节点数为22936个。浪向角取为0°～180°，每15°为1个间隔，共计13个浪向。圆频率范围为0.2～1.8rad/s，每0.05rad/s为1个间隔。计算结果表明，纵荡和横荡等无回复力运动响应最大值出现在低频范围内，当波浪频率增大时，响应幅值迅速减小。与之相反，平台横摇和纵摇响应最大值出现在常规波频范围内，分别为1.05rad/s和0.75rad/s，对应波长分别为56m和107m，一般该波长范围内组成波的波幅不会很大，表明平台抗横摇和纵摇的性能较好。垂荡响应最大值出现在低频范围内，大小接近于1，表示平台随长波的整体沉浮，除了最大值以外，另有一处极大值出现在0.55rad/s波频处，对应波长为180m；此时响应RAO幅值约为0.7，小于波幅，表明垂荡运动不会被波浪运动放大。平台的质量分布均匀且对称性较好，艏摇运动整体较小。

4 平台-系泊系统耦合动力响应计算结果

根据作业海域的实际特点选取计算工况。观测结果表明：作业海域最大流速对应的水流方向常年不变，故流向角恒取350°，流速取50a一遇最大值1.7m/s；-45°～135°范围内的波浪较大，其他方向的波浪常年较小，故浪向角取为0°、45°、90°、135°和315°，浪高取50a一遇值（见表2）。风速取50a一遇最大值，即27m/s，方向与浪向相同。计算工况分为完整工况和破损工况，其中破损工况指任意一根锚链损坏时的自存工况。完整工况和破损工况下的安全系数分别取1.67和1.25，每个工况模拟时长为3h的短期海况，时间步长为0.2 s。

表2 作业区域50a一遇浪高

采用SESAM.DeepC时域模拟平台-系泊系统的耦合运动响应，基于挪威船级社规范，取锚链纵向拖曳力系数和横向拖曳力系数分别为C=1.4、C=2.6，取NPD（Norwegian Petroleum Directorate）谱为风谱模型，取三参数JONSWAP谱为波浪谱模型。平台和锚链的浪载荷、流载荷均采用Morison公式计算。为简便起见，在计算风载荷时，将平台水面以上部分简化为具有相同长、宽、高的密实长方体，采用文献[11]相关规定计算风载荷。由于平台水面以上部分较小，风载荷不大，故不会产生大的误差。

以完整工况45°浪向角为例，给出6 号锚链顶端拉力的时历曲线和拉力响应谱，其中时历曲线呈随机变化特征（见图2）。响应谱主峰值对应频率为0.93rad/s，对应波频振荡；在0.67rad/s 频率附近出现一处小峰值，对应低于波频的二阶力；在极低频（趋于0rad/s）附近也出现一个小峰值，对应二阶力中的定常部分，由平台的整体漂移导致。将图2 中的拉力时历曲线进一步分解为低频部分（二阶力）和高频部分（波频振荡），结果见图3。由于包含了漂移力，低频部分的平均拉力较大，但拉力变化范围较小；高频部分曲线在0 点附近振荡，拉力变化范围较大。由于锚链强度与最大拉力有关，因此锚链强度对定常漂移力更加敏感。

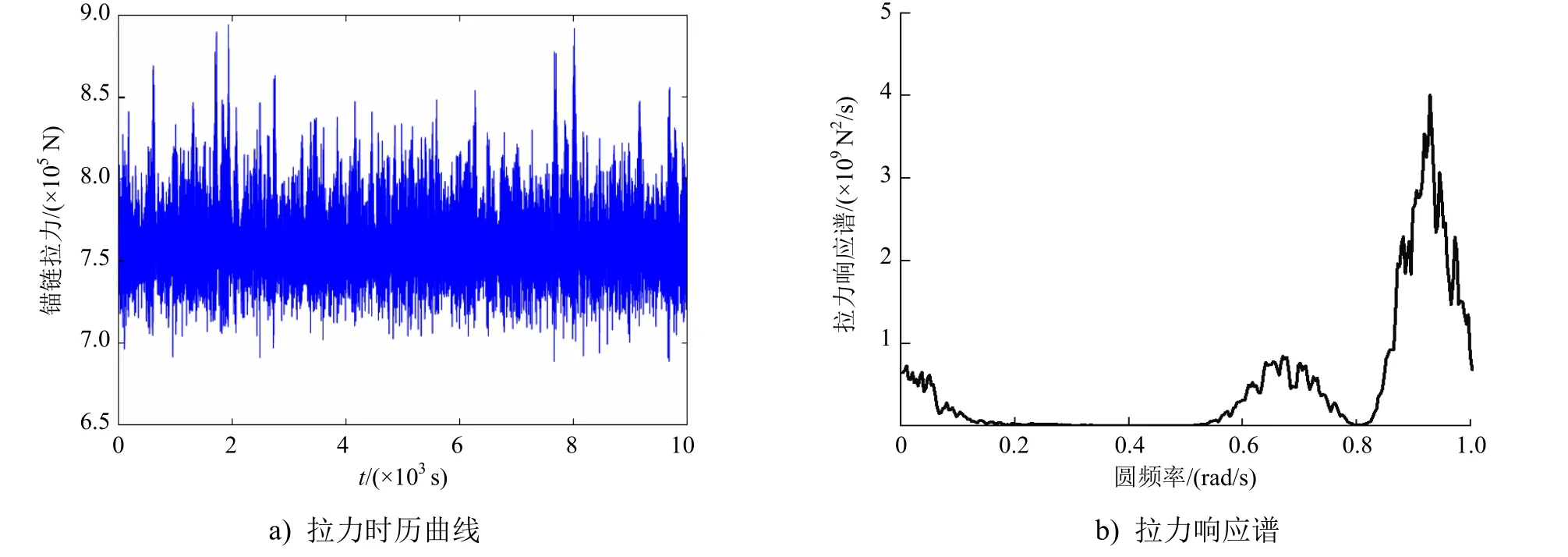
图2 完整工况45°浪向角下锚链6 顶端拉力时历及频谱

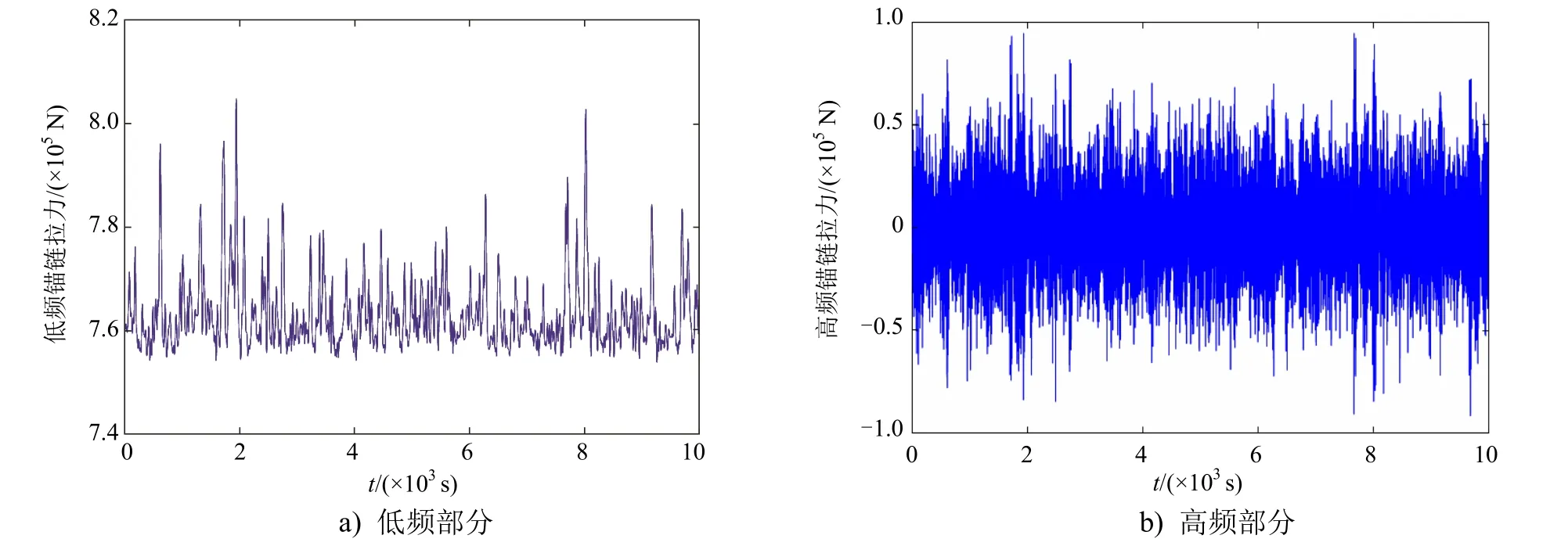
图3 完整工况45°浪向角下锚链6顶端拉力时历高低频分解

图4 为完整工况不同浪向角下各锚链的最大拉力。由图4可知，45°浪向角下的锚链拉力最大，315°浪向角下的锚链拉力最小，且最大拉力总出现在6号锚链处，距离6号锚链较远的锚链拉力较小，这是由于6号锚链与流向接近共线，而海流是导致整体漂移力增大的关键因素。图4中不同浪向角下的锚链拉力相差不大，这也表明波和风载荷的影响较小。完整工况下最大锚链拉力为895kN，小于许用拉力1884kN。

根据工程经验，一般最大受力锚链相邻的锚链损坏是最危险的情况，基于以上讨论，破损工况取为45°浪向角下4～9 号锚链任意一根锚链破损。图5 为破损工况下各锚链最大静态拉力。由图5 可知，4～9 号锚链中任意一根锚链破损均会导致相邻锚链有不同程度的载荷增加，其中5 号锚链破损导致的载荷最大，而1～3号锚链和10～12 号锚链的载荷变化不大。除了6 号锚链自身破损以外，其余破损工况下的最大载荷均出现在6 号锚链上。破损工况下最大锚链拉力为1244kN，相比完整工况增加了39%，小于许用拉力2517kN。