C与SiO2反应的热力学分析

潘书恒 程萍

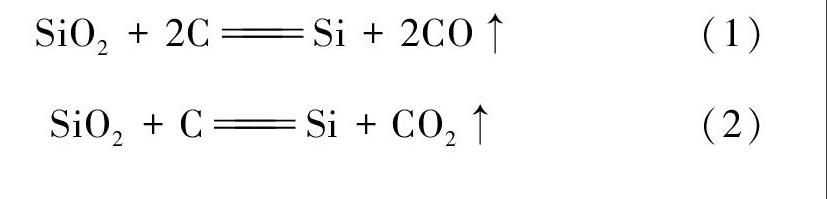
摘要： 从热力学角度分析C与SiO2反应生成CO而非CO2的原因;指出在实际生产温度下，Si和SiO2均呈液态，理论上不应引用298K时的生成焓与标准熵;计算了2200K时反应的热力学函数，并进一步讨论了298～2500K温度范围内反应焓变与熵变对298K时相应数值的偏离情况，绘制了较精确的ΔrGθm-T图;发现对于C与SiO2的反应而言，在此温度范围内，热力学函数对298K时相应数值的偏离程度较小。

关键词： C与SiO2反应; 非常温反应; 物态变化; 热力学分析

文章编号： 1005-6629（2021）02-0091-08

中图分类号： G633.8

文献标识码： A

1  问题的提出

在高中元素化合物知识的学习中，学生常常会对一些化学反应产生疑惑，其中一例便是： 为什么C与SiO2反应得到的产物是CO，而不是CO2？对于这一问题，如果教师以“实验事实就是如此”回应学生，将不利于学生探究与质疑精神的发展，甚至可能给学生留下“化学反应不讲理，需要死记硬背”的不良印象。从热力学角度对该反应展开讨论，分析C与SiO2反应生成CO的原因，同时分析不同温度下反应的焓变与熵变对298K时相应数据的偏离情况，可为从热力学角度研究非常温反应，尤其是物质的物态与298K时不同的反应，提供一种思路。

2  C与SiO2的反应

对于C与SiO2反应为什么生成CO这一问题，有些教师一般解释为： 由于实际生产中C是过量的，即使反应生成了CO2，后者在高温下也会进一步与C反应，最终生成CO。这样的解释乍一看很合理，然而可能會引起学生这样的认识： 如果是少量C与过量SiO2反应，应该就能生成CO2。实际情况真是如此吗？

2.1  C与SiO2反应的热力学分析

化学热力学研究化学反应的方向和限度问题，对于一个等温等压不做非体积功的反应，如果以反应中各物质的浓度或压力为1mol·kg-1或100kPa为研究状态，那么可以用标准摩尔反应吉布斯自由能变ΔrGθm（简称为反应自由能）判断反应的自发性。若ΔrGθm<0，表示反应在标准状态下能正向自发进行;反之，若ΔrGθm>0，则反应在标准状态下逆向自发进行。ΔrGθm与反应温度相关，在一定温度（T）下，ΔrGθm（T）=ΔrHθm（T）-TΔrSθm（T），其中ΔrHθm与ΔrSθm分别为标准摩尔反应焓变（简称为反应焓）和标准摩尔反应熵变（简称为反应熵），若它们的量值随温度变化较小，常用298K时的量值代替。ΔrHθm与ΔrSθm可由反应中各物质的标准摩尔生成焓ΔfHθm（简称为生成焓）与标准摩尔熵Sθm（简称为标准熵），通过公式ΔrHθm=∑νBΔfHθm（B）与ΔrSθm=∑νBSθm（B）计算得出，式中B表示反应物或生成物，νB表示反应物或生成物在方程式中的计量数，对生成物νB取正值，反应物νB取负值[1]。

对于C与SiO2反应得到何种氧化产物的热力学分析，即是考察下述反应（1）和（2）的反应自发性。反应中相关物质在298K时的生成焓与标准熵如表1所示注： 本文中所有热力学数据均取自叶大伦主编《实用无机物热力学数据手册（第2版）》[2]。;根据表1不难算得两个反应的焓变和熵变，进而得到反应自由能的表达式;令ΔrGθm=0，即可得到反应的转化温度，如表2所示。

SiO2+2CSi+2CO↑（1）

SiO2+CSi+CO2↑（2）

从表2可看出，两个反应都是吸热、熵增的反应，升高温度有利于反应正向进行。当反应温度高于1914.2K时，反应（1）（生成CO）在热力学上能自发进行;当温度高于2808.0K时，反应（2）（生成CO2）在热力学上能自发进行。工业上制粗硅的实际生产温度在1800～2000℃[3]，即2073～2273K，超过了反应（1）的转化温度，但未达到反应（2）的转化温度。故在实际生产条件下，C还原SiO2得到的氧化产物为CO。

将两个反应的ΔrGθm随温度的变化情况绘于图1，从图中不难看出，随着温度升高，两个反应的ΔrGθm数值都越来越小，说明反应倾向性逐渐增大。但需要注意的是，仅凭此图不宜作出如下判断： 由于同一温度时，反应生成CO的ΔrGθm始终低于生成CO2的ΔrGθm，

说明反应更倾向于生成CO，因而C还原SiO2始终只能得到CO。这一判断的问题在于，忽略了ΔrGθm只能用于判断一个反应自身的反应自发性，而不能用于比较不同反应的倾向性大小。吴国庆教授曾写文指出[4]，不能用Fe3O4的生成自由能ΔfGθm数值比FeO、 Fe2O3更小，来说明Fe在O2中燃烧为何生成Fe3O4，因为不同反应的ΔrGθm之间不具有可比性;而要对比铁和氧化合生成上述三种氧化物的反应倾向性大小，最简单的理论模型是考察它们相互转化反应的自发性，如反应4Fe3O4+O26Fe2O3的ΔrGθm。

那么，反应生成的CO是否有可能进一步还原SiO2而得到CO2呢？不妨考察下述反应（3）的自发性：

SiO2+2COSi+2CO2（3）

由表1不难求得，298K时反应（3）的ΔrHθm=342.43kJ·mol-1， ΔrSθm=7.66J·K-1·mol-1，同样是吸热、熵增的反应，但转化温度高达44704K，即反应（3）实际上无法发生，故C与SiO2反应生成CO在热力学上是稳定的。

2.2  高温致物态发生变化的反应热力学分析

仔细审视图1不难发现问题： 直线不可能无限延伸。根据ΔrGθm=ΔrHθm-TΔrSθm可知，直线的斜率即-ΔrSθm。严宣申教授指出[5]，不同温度下反应的ΔrHθm和ΔrSθm近似为定值的条件是各物质的物态应和298K时相同。而随着反应温度的提高，Si和SiO2的物态将由固态变为液态，甚至是气态;因而在物态发生变化后，理论上不应再引用298K时的ΔrHθm和ΔrSθm数值，ΔrGθm-T图也不会是直线。

事实上，Si和SiO2的熔点分别为1685K和1996K，在实际生产温度下（2073～2273K）均为液态，因而上述分析中引用298K时的ΔrHθm和ΔrSθm数值并不严谨。

在本文引用的《实用无机物热力学数据手册》中，可以查到反应中各物质在2200K时的生成焓与标准熵，经计算可得反应的反应焓、反应熵与转化温度，如表3所示。

从表3可以看出，2200K时两个反应的ΔrHθm和ΔrSθm与298K时的数值相比，变化并不大;转化温度的差值也不足30K。由于反应（3）（SiO2+2COSi+2CO2）的焓变和熵变可通过盖斯定律得到： （3）=（2）×2-（1），因而可推断反应（3）的相应数值也无明显变化。故2.1的结论在2200K时仍然成立。

这是偶然现象吗？还是说，由于Si和SiO2在2200K时都呈液态，且一为反应物一为生成物，这种相变引起的物质热力学函数的变化在计算反应的热力学函数时被抵消了？是不是当反应中只有一种物质发生相变时，这种差异就会显著出现呢？要回答这些问题，需要对不同温度下反应焓变与熵变对298K时数值的偏离情况进行研究。

2.3  不同温度下ΔrHθm（T）和ΔrSθm（T）对ΔrHθm（298K）和ΔrSθm（298K）的偏离

当一定温度范围内，反应中各物质均不存在物态变化时，根据反应焓、反应熵与温度的关系，有[6]：

ΔrHθm（T2）=ΔrHθm（T1）+∫T2T1ΔCpdT（1）

ΔrSθm（T2）=ΔrSθm（T1）+∫T2T1ΔCpTdT（2）

式中ΔCp=∑νBCp， m（B）， Cp， m（B）表示反應物或生成物的等压摩尔热容，νB表示物质在反应中的计量数。

Cp， m、 ΔCp与T的关系可以用经验式表示[7]：

Cp， m=A1+A2×10-3T+A3×105T-2+A4×

10-6T2（J·K-1·mol-1）（3）

ΔCp=∑νBCp，m（B）=ΔA1+ΔA2×10-3T+ΔA3×

105T-2+ΔA4×10-6T2（4）

式中Ai为常数，ΔAi=∑νBAi（B）， i=1～4。

而当温度范围内存在物态变化时，由于相变物质Cp， m的变化，及相变焓与相变熵的存在，反应的焓变与熵变需分段计算。

C与SiO2的反应中，各物质的A1～A4数值及相变焓与相变熵如表4所示。取表4中各物质的公共温度范围（298～2500K）为研究对象，以物质的A1～A4数值出现变化为依据对公共温度范围分段，可算得两个反应在各温度段下的ΔA1～ΔA4。

将ΔA1～ΔA4代入∫T2T1ΔCpdT与∫T2T1ΔCpTdT，得到关于T的多项式，运用Origin 2017软件的函数计算功能，可得积分项在各温度区间内的数值范围及变化情况，如表5所示。

物态变化对ΔrHθm和ΔrSθm的影响可通过图2的反应模型得到： 当生成物发生相变时，

相变焓与相变熵对反应的焓变与熵变有正贡献;相反，当反应物发生相变时，相变焓与相变熵对反应的焓变与熵变有负贡献。以计算1000K时反应（1）的ΔrHθm为例： 在298K到1000K的温度范围内，在543K时反应物SiO2发生了晶型转变，若用ΔHCT（SiO2）表示SiO2晶型转变中的相变焓，则有ΔrHθm（1000K）=ΔrHθm（298K）+∫543298ΔCpdT-ΔHCT（SiO2）+∫1000543ΔC′pdT;反应熵变的计算方法与此类似，不作赘述。

TM（B）：A（s）ΔrHθm（TM，1）B（s）

ΔH=0ΔHM（B）

TM（B）：A（s）ΔrHθm（TM，2）B（1）

ΔrHθm（TM，2）=ΔrHθm（TM，1）+ΔHM（B）

TM（A）：A（s）ΔrHθm（TM，1）B（s）

ΔHM（A）ΔH=0

TM（A）：A（1）ΔrHθm（TM，2）B（s）

ΔrHθm（TM，2）=ΔrHθm（TM，1）-ΔHM（A）

注： TM（B）表示B的熔点，ΔHM（B）表示B的相变焓;TM（A）和ΔHM（A）含义类似。相变熵对反应熵变影响的分析与此相同。

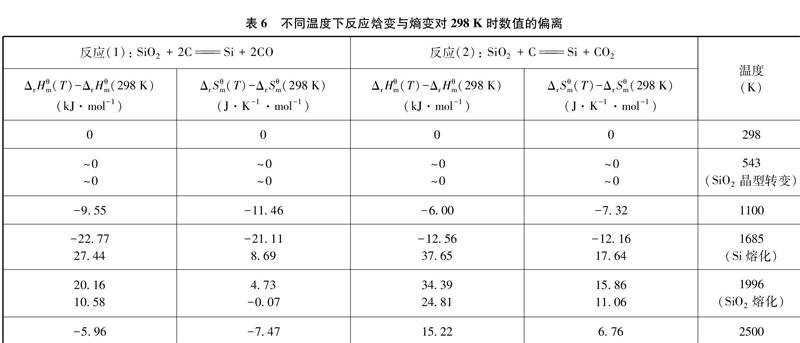
同时考虑积分项与物态变化对ΔrHθm和ΔrSθm的影响，可得不同温度下反应焓变与熵变对298K时数值的偏离情况，如表6、图3和图4所示。

从上述图表中不难得到以下信息： 对于C还原SiO2的反应而言，不论生成CO还是生成CO2，在温度较低、各物质物态与298K相同时（298～543K），ΔrHθm和ΔrSθm对298K时数值的偏离很小，可几乎视为定值;而当反应中仅反应物的物态与298K不同时（543～1685K），随温度升高，这种偏离逐渐增大;当反应中生成物也发生物态变化时，这种偏离可能因抵消而减小[图4中1685K前后反应（1）的情况]，也可能反向增大[图3中1685K前后两个反应的情况，及图4中1685K前后反应（2）的情况];而从整体来看，在298～2500K的温度范围内，对反应（1）而言，ΔrHθm（T）对ΔrHθm（298K）（687.27kJ·mol-1）的最大偏离值为27.44kJ·mol-1，最大偏离率为4.0%;ΔrSθm（T）对ΔrSθm（298K）（359.04J·K-1·mol-1）的最大偏离值为-21.11J·K-1·mol-1，最大偏离率为5.9%。对反应（2）而言，ΔrHθm（T）对ΔrHθm（298K）（514.85kJ·mol-1）的最大偏离值为37.65kJ·mol-1，最大偏离率为7.3%; ΔrSθm（T）对ΔrSθm（298K）（183.35J·K-1·mol-1）的最大偏离值为17.64J·K-1·mol-1，最大偏离率为9.6%;两个反应的最大偏离点均位于Si熔化前后，最大偏移率均在10%之内。

同时不难发现，一个反应的焓变与熵变对298K时相应数值的偏离程度未必随温度的升高而增大;物态变化也未必导致偏离程度的增大;偏离程度取决于反应的ΔCp及相变情况（包括与298K时的物态相比，存在一次相变还是多次相变，相变物质是反应物还是生成物，相变焓与相变熵的相对大小等），需要具体问题具体分析。

2.4  不同温度下反应的ΔrGθm与温度的关系

将表6中各温度区间内反应焓变与熵变对298K时相应数值偏离值的均值，作为该温度区间反应焓变与熵变偏离值的代表。例如，1100～1685K范围内反应（1）的焓变偏离值，即取表6中1100K和1685K时相应偏离值（-9.55和-22.77）的均值-16.16，此时这种近似处理引入的最大误差为[（-16.16）-（-22.77）]/687.27=1.0%。

经计算，对两个反应在各温度区间内的反应焓变与熵变偏离值做这种均值近似处理

引起的误差≤2.1%，可以忽略不计。用此种均值近似方法得到的反应焓变、熵变、自由能，与2.1中将反应焓变与熵变视为298K下定值时算得的自由能，前者对后者的偏离值如表7所示，两种方法得到的ΔrGθm-T对比图如图5所示。

从图5可看出，C与SiO2反应的ΔrGθm-T图并非是一条直线，但与将反应焓变与熵变视为定值得到的ΔrGθm-T直线图间的偏离不大;可见，在298～2500K的温度范围内，即使物质的物态发生了变化，引用298K时的反应焓变与熵变也不致引起较大偏差。

但需注意的是，这一结论不能无限外推，尤其是当反应中一种物质的物态变为气态后，

反应熵可能出现明显的变化，此时ΔrGθm-T图可能出现明显的转折点，见图6[8][沸点： b.p.（Hg）=630K， b.p.（Mg）=1364K， b.p.（Ca）=1757K]。

3  结语

热力学分析表明，C与SiO2反应倾向于生成CO;在实际生产温度下，生成CO2的反应是非自发的。当Si和SiO2的物态与298K时不同时，理论上不应引用298K时物质的生成焓与标准熵数据。但通过计算发现，对于C与SiO2的反应而言，在298～2500K的温度范围内，反应的焓变与熵变对298K时数值的偏离程度不大（10%以内），最大偏离点位于Si熔化前后;同时，该温度范围内反应的ΔrGθm-T图，接近将反应焓变与熵变视为定值得到的ΔrGθm-T直线图。但这一结论不能无限外推，对于一般的反应而言，这种偏离程度需根据反应的ΔCp及相变情况作具体分析。

参考文献：

[1][6]傅献彩， 沈文霞， 姚天扬等. 物理化学·上册（第5版）[M]. 北京： 高等教育出版社， 2005： 105， 113.

[2][7]叶大伦， 胡建华. 实用无机物热力学数据手册（第2版）[M]. 北京： 冶金工业出版社， 2002.

[3]人民教育出版社， 课程教材研究所， 化学课程教材研究开发中心. 化学（必修第二册）[M]. 北京： 人民教育出版社， 2020： 22.

[4]吴国庆. 铁丝在氧气里燃烧的产物[J]. 中学化学教学参考， 2002， （6）： 9～10.

[5]嚴宣申. 谈化学热力学状态函数的运用[J]. 化学教育， 2011， 32（1）： 73～77.

[8]严宣申. 化学原理选讲[M]. 北京： 北京大学出版社， 2012： 35.