预防暂态低频减载的储能容量配置多目标动态优化方法
2021-03-18刘庆楷刘明波陆文甜
刘庆楷,刘明波,陆文甜
(华南理工大学电力学院,广州市 510640)
0 引 言
电网频率是衡量电力系统中有功功率与负荷平衡的重要指标。如果大型电力系统由于发电损失而导致有功功率不足,将会使得系统频率下降。频率的下降首先由同步发电机的旋转惯性阻止,然后同步发电机调速器动作,阻止系统频率的进一步下降,这2个事件一般在事故发生后的几十秒内完成。当系统遭遇大扰动如直流闭锁或大机组脱机时,电网频率快速跌落,当其达到系统频率的限制值时,电网的低频减载将会启动,自动切除部分负荷,以保证系统稳定运行。实际上,在某些故障下,系统有足够的能力使稳态频率恢复到低频减载的触发频率值之上,然而由于暂态过程中系统频率的快速跌落,仍会导致暂态低频减载的触发[1]。如果能在系统受到大扰动时,快速向电网注入一定的有功功率,就能避免暂态低频减载事件的发生,这对于增强电力系统的可靠性、减少切负荷导致的经济损失而言,具有重要意义。储能由于具有充放灵活,响应速度快的特点[2-6],可以快速响应系统频率变化,被认为是预防电网暂态低频减载的重要手段之一。
近年来,针对储能参与电网快速调频的研究已经取得了不少成果。文献[7]将储能等值成虚拟同步发电机,结合小信号线性化的系统模型,优化整个线性系统的H2范数以获得最优的储能虚拟惯性控制参数。文献[8]提出了一种基于线性二次型调节器的储能自适应控制方法,通过线性二次型调节器技术,确定最优的状态反馈增益,并根据系统的实时频率反馈调节储能参数,以满足系统的调频需求。文献[9]提出了一种基于储能的自调节虚拟同步发电机控制方法,在虚拟同步发电机运行期间连续搜索最优参数,以最小化系统频率的变化幅度。然而,上述研究在设计储能的控制策略或优化储能的控制参数时主要关注系统整体的频率响应质量,忽略了控制过程中储能的功率和能量限制。并且,上述控制方法均没有对暂态调频过程中的系统频率值进行硬性限制,不能预防电网暂态低频减载事件的发生[10]。
为了合理考虑储能的功率和能量容量限制,同时预防电网暂态低频减载,文献[11]针对墨西哥某实际独立电网,以最小化储能配置成本为目标,将储能的容量约束和系统频率约束加入到动态模型中,联合优化储能的控制系数和参与快速调频的储能容量,以避免电网在严重事故发生时触发低频减载。文献[12]针对澳大利亚的某个实际微电网,采用灰狼优化算法,同时优化储能参数和参与微电网快速调频的能量值,以最小储能配置成本获得满足系统要求的频率响应。文献[13]从理论上推导了暂态过程中系统频率变化的非线性表达式并对其进行线性近似,并在此基础上得到预防电网暂态低频减载的最优储能参数与容量配置。上述文献将储能的容量约束和系统频率约束加入到动态优化模型中,并以最小化储能成本为目标对预防电网暂态低频减载的储能进行配置。然而,上述文献对储能的输出功率约束均采用简单的上下限不等式约束描述,不能准确描述储能的输出功率限制。由此得出的储能功率容量配置结果为功率不加限制时的储能输出功率最大值,不一定为储能在最优控制参数下对应的最优储能功率容量,在最优控制参数下,存在更小的储能功率容量可以满足系统频率安全约束[14]。为了解决以上问题,本文采用基于储能饱和输出限幅环节的分段函数约束对储能的输出功率进行精确表达。
此外,上述预防暂态低频减载的储能容量配置模型中,都只考虑储能的配置成本目标,由此得到的最优储能配置方案在应对预想的大扰动时,将使得系统频率的最低点容易靠近低频减载的触发值,缺乏安全裕度[15]。因此,本文提出一种预防暂态低频减载的储能容量多目标动态优化模型,旨在同时考虑储能配置成本和暂态频率调节性能2个相互冲突的目标。为精确表示储能的功率输出限制,采用具有分段函数约束的储能动态模型,并采用大M法对分段函数约束引入的非线性问题进行处理。然后采用隐式梯形积分法将多目标动态优化模型转化为多目标混合整数二次规划模型。最后采用规格化法平面约束法和CPLEX求解器获得上述多目标储能容量配置问题的帕累托最优解。
1 电力系统等值频率响应模型
本文主要研究电力系统需要储能参与快速调频的场景,主要考虑电力系统的固有频率特性与一次调频过程,而二次调频由于时间尺度较大,不在本文的考虑范围之内。在一个具有N台发电机的多机系统之中,假设所有发电机以相同的频率摆动,可以获得图1所示的含储能的电力系统等值频率响应模型[1]。

图1 电力系统等值频率响应模型Fig.1 Equivalent frequency response model of power system
假设t=t0时,电力系统发生了一个大的扰动(如直流闭锁、机组脱机、负荷突增等),根据图1的频率响应模型,可以得到频率与不平衡功率之间的微分方程表达式:
(1)
式中:Heq为多机系统的等值惯性常数;f0为电力系统标称频率;Deq为负荷阻尼系数;Δf(t)为电力系统实际频率与标称值的偏差值;ΔPm(t)为发电机一次控制器提供的机械功率增量;ΔPess(t)为储能注入网络的功率;ΔPe(t)为大扰动中损失的功率或者突增的负荷功率。
等值惯性时间常数的计算公式为:
(2)
式中:SB,i为系统中同步发电机i的额定功率;Hi为同步发电机i的惯性常数;SB为系统的基准功率。
根据图1,同步发电机一次控制器提供的机械功率增量可以用含等值调速器-涡轮机时间常数Tg和等值下垂系数R的一阶模型表示,写成微分方程的形式为:
(3)
等值下垂系数R可由各发电机的下垂系数Ri计算得出:
(4)
在本文中,储能采用PD控制器及限制环节进行等效。采用PD控制,储能部分的注入功率与系统的频率变化率成正比,可以有效降低暂态过程中的系统频率变化率。而且在频率下降的过程中,PD控制器可以快速感知电网的频率变化,迅速增加储能的输出功率,提供快速调频服务,起到支撑电网频率的作用[16]。由于限制环节的存在,储能的实际输出功率为分段函数形式。假设储能初始的输出功率为0,储能的实际输出功率ΔPess(t)可表示为:
(5)
式中:Pmaxess为储能输出功率上限,即为储能所需要配置的功率容量;ΔPchoose(t)表示采用PD控制器后不加限制的储能理想输出功率,根据图1可表示为:
(6)
式中:KD、KP代表PD控制器的控制参数;Tess代表储能的时间常数;X(t)为引入的中间变量。
2 含分段函数约束的多目标动态优化模型
本文考虑的多目标优化问题包括2个目标:一是最小化储能容量配置成本;二是最优化系统的暂态频率调节性能。储能配置成本分为功率容量成本和能量容量成本。储能的功率容量决定了储能在整个频率响应过程中输出功率的上限,能量容量决定了储能参与调频过程的持续时长。为了量化系统的暂态频率调节性能,本文将暂态过程中频率偏差平方的积分值作为目标之一加入到优化问题之中,结合第1节的电力系统等值频率响应模型,构造出具有分段函数约束的多目标动态优化模型。
2.1 目标函数
第1个目标函数为最小化储能的配置成本,考虑储能的功率容量与能量容量,可得:
minf1=c1Pmaxess+c2Emaxess
(7)
式中:Emaxess为储能需要配置的能量容量;c1和c2分别为单位功率与单位能量成本。
第2个目标为最优化调频过程中的性能指标。由于暂态过程中频率偏差的正负性不定,所以本文将频率偏差的平方值在整个暂态过程中的积分值作为目标函数,用于衡量储能参与系统快速调频的效果[2]。
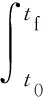
(8)
式中:t0为暂态过程开始的时刻;tf为暂态过程结束的时刻。
2.2 约束条件
2.2.1系统动态频率特性约束
在本文中,系统的动态频率特性包括系统的固有频率特性约束、发电机一次调频特性约束以及储能的输出功率约束,即为由式(1)、式(3)、式(5)、式(6)组成的微分方程组,用紧凑的形式来表达,如式(9)所示:
f(x,Pmaxess)=0
(9)
式中:x=[Δf(t), ΔPm(t), ΔPess(t), ΔPchoose(t)]T,为电力系统等值频率响应模型的状态变量。
2.2.2储能运行约束
储能在参与调频的动态过程中,除了需要满足式(5)和式(6)所示的输出功率约束之外,还须满足如下运行约束条件:
(10)
ΔPd(t)+ΔPc(t)=ΔPess(t)
(11)
ΔPd(t)·ΔPc(t)=0
(12)
(13)
式中:ΔPd(t)代表储能系统放电功率;ΔPc(t)代表储能系统充电功率;ηd代表储能系统的放电效率;ηc代表储能系统的充电效率。式(10)代表储能的能量转移约束。
同时,为了延长储能的使用寿命,避免储能过充过放,储能的荷电状态(state of charge,SOC)应维持在合理的范围之内:
CSOCminEmaxess≤Eess(t)≤CSOCmaxEmaxess
(14)
式中:CSOCmin、CSOCmax分别为储能荷电状态的下限和上限。
2.2.3系统运行安全约束
如上文所述,配置储能的目的是在系统发生严重事故后,通过储能的快速出力避免暂态低频减载的发生,因此引入了暂态过程中系统运行的安全约束:
Δfmin≤Δf(t)≤Δfmax
(15)
(16)
式中:Δfmax和Δfmin分别为最大和最小频率偏差值。式(15)为系统频率的安全约束,在暂态过程中系统的频率不得小于低频减载的触发频率,同时也不能大于系统规定的频率上限;式(16)为系统频率变化率(rate of change of frequecny, RoCoF)约束,在暂态过程中系统的频率变化率不得大于系统规定的最大值以保证系统的安全运行。
3 将多目标动态优化模型转化为多目标混合整数二次规划模型
第2节所提的多目标动态优化问题难以直接求解,本节采用大M法[17]和隐式梯形积分法,将本文提出的多目标动态优化模型转化为多目标混合整数二次规划模型。
3.1 微分方程与积分方程代数化
将式(8)由积分方程写成代数方程,可得:
(17)
式中:tk代表第k个具体的时刻;h代表步长;n代表总时刻数。
通过隐式梯形积分法将微分方程式(1)、式(3)、式(6)转化为代数方程,可得:
(18)
ΔPm(tk+1)-ΔPm(tk)=
(19)
(20)
(21)
ΔPimba(tk)=ΔPm(tk)+ΔPess(tk)-
ΔPe(tk)-DeqΔf(tk)
(22)
将储能能量转移约束的积分表达式式(10)代数化。设储能参与调频的初始能量值为最大能量值Emaxess的α倍(0<α<1),把式(10)由积分形式改写成差分形式:
Eess(0)=αEmaxess
(23)
Eess(tk+1)=Eess(tk)-h[ΔPd(tk)/ηd+ΔPc(tk)ηc]
(24)
3.2 储能运行约束线性化处理
本文采用大M法对非线性约束式(12)及分段函数式(5)进行线性化处理。
1)对非线性的式(12),在时刻tk引入一个整数变量U1(tk),得到差分后的ΔPd(tk)与ΔPc(tk)的线性化表达式:
0≤Pd(tk)≤M[1-U1(tk)]
(25)
-MU1(tk)≤Pc(tk)≤0
(26)
式中:M为一个充分大的正数。
2)对储能输出功率的分段函数表达式,将式(5)改写为:
(27)
式中:Nbig是一个充分大的正数。
在时刻tk引入3个0-1变量Z1(tk)、Z2(tk)、Z3(tk),以及3个连续变量ΔPess1(tk)、ΔPess2(tk)、ΔPess3(tk),通过大M法可以将式(27)式转化为:
ΔPess(tk)=ΔPess1(tk)+ΔPess2(tk)+ΔPess3(tk)
(28)
Z1(tk)+Z2(tk)+Z3(tk)=1
(29)
-Nbig-ΔPchoose(tk)≤M[1-Z1(tk)]
(30)
ΔPchoose(tk)-(-Pmaxess)≤M[1-Z1(tk)]
(31)
-Pmaxess-ΔPchoose(tk)≤M[1-Z2(tk)]
(32)
ΔPchoose(tk)-Pmaxess≤M[1-Z2(tk)]
(33)
Pmaxess-ΔPchoose(tk)≤M[1-Z3(tk)]
(34)
ΔPchoose(tk)-Nbig≤M[1-Z3(tk)]
(35)
-MZ1(tk)≤ΔPess1(tk)≤MZ1(tk)
(36)
-MZ2(tk)≤ΔPess2(tk)≤MZ2(tk)
(37)
-MZ3(tk)≤ΔPess3(tk)≤MZ3(tk)
(38)
ΔPess1(tk)≤-Pmaxess+M[1-Z1(tk)]
(39)
ΔPess1(tk)≥-Pmaxess-M[1-Z1(tk)]
(40)
ΔPess2(tk)≤ΔPchoose(tk)+M[1-Z2(tk)]
(41)
ΔPess2(tk)≥ΔPchoose(tk)-M[1-Z2(tk)]
(42)
ΔPess3(tk)≤Pmaxess+M[1-Z3(tk)]
(43)
ΔPess3(tk)≥Pmaxess-M[1-Z3(tk)]
(44)
至此,经过大M法和隐式梯形积分法的处理,本文提出的多目标动态优化模型可以转化为如下的多目标混合整数二次规划问题:
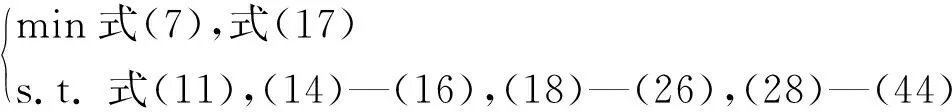
(45)
对于转化后的多目标混合整数二次规划问题,可以采用规格化法平面约束法[18-19]将其转化为一系列单目标混合整数二次规划问题,再对得到的单目标优化问题调用CPLEX求解器进行求解。本文所提方法的流程如图2所示。
4 算例分析
为验证本文所提多目标动态优化模型与所提算法的可行性与有效性,本文采用IEEE 24节点系统进行仿真计算。储能的类型采用主流的磷酸铁锂电池,其充放电效率都设为90%,即ηd=ηc=0.9,储能的单位功率成本c1为1 100元/kW,单位容量成本c2为2 000元/(kW·h)[20]。该系统的接线如图3所示。其总负荷为2 850 MW,该系统的基准功率为100 MV·A,额定频率为50 Hz,低频减载触发的触发频率为49.5 Hz[5],系统允许的最大频率变化率为0.5 Hz/s,仿真的持续时间为100 s,储能的接入节点为22号节点。系统频率响应模型的等值参数[21]、SOC上下限[22]以及优化所需的其他参数如表1所示。
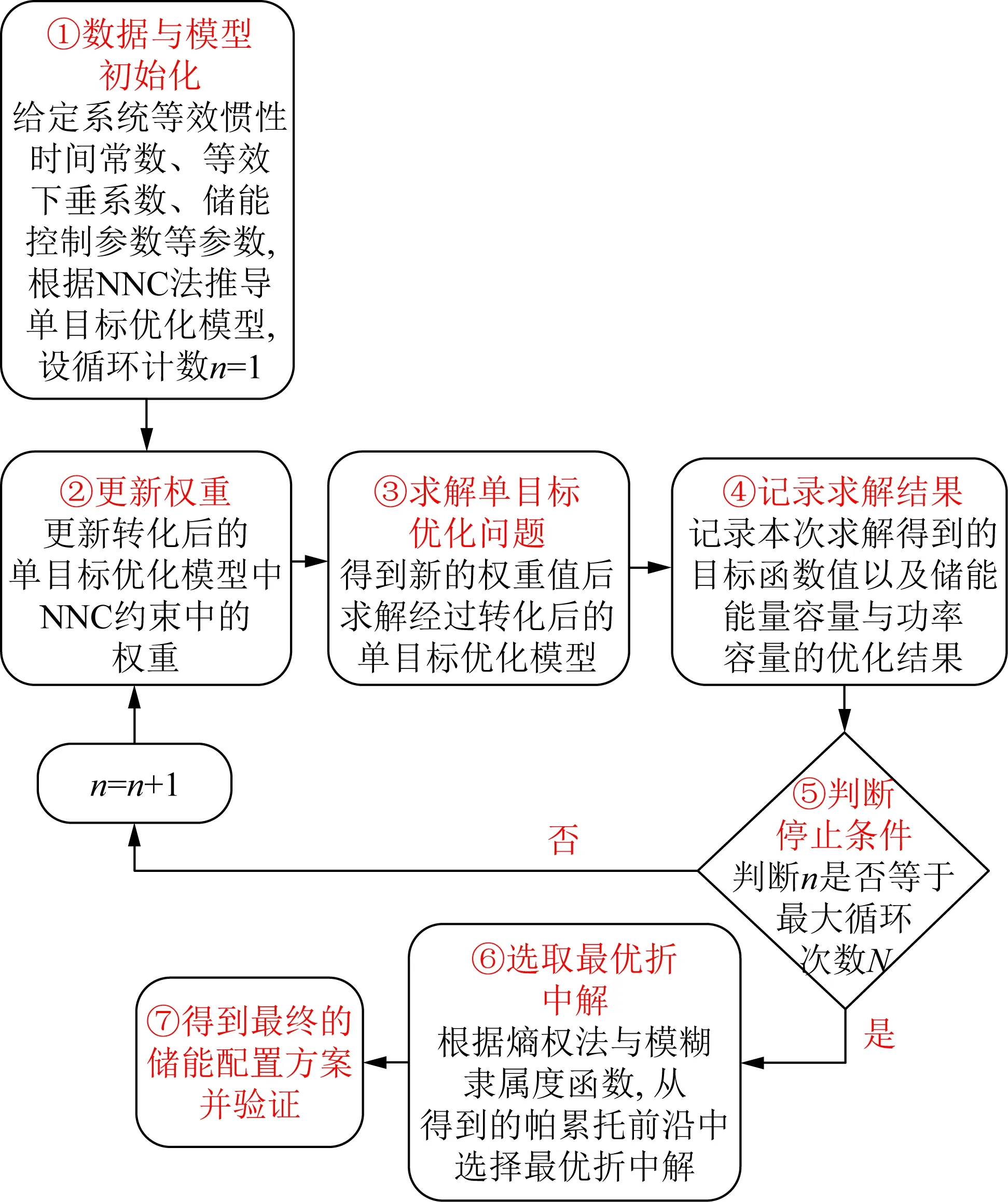
图2 多目标动态优化流程Fig.2 Flowchart of the multi-objective dynamic optimization
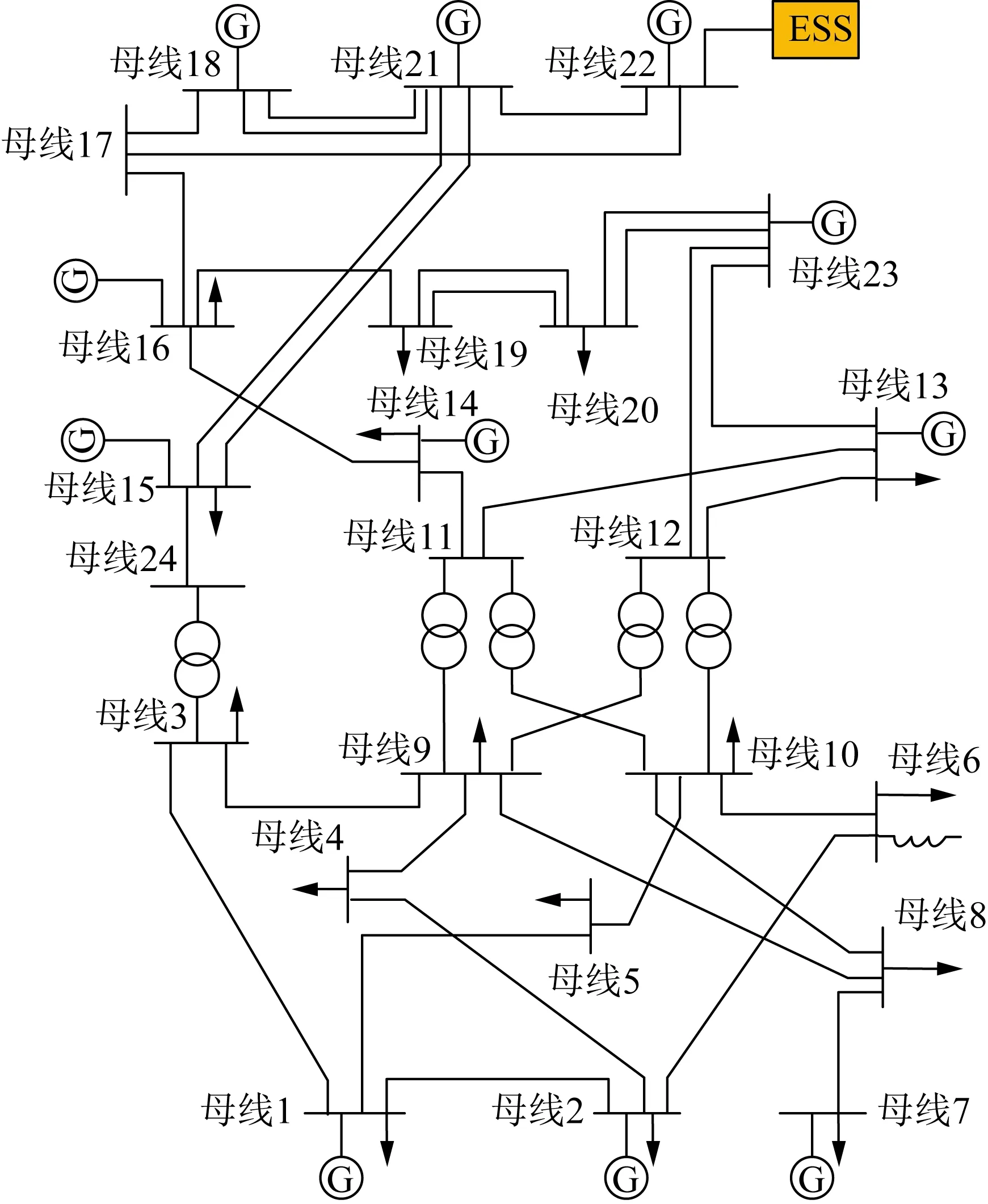
图3 IEEE 24节点系统接线图Fig.3 Connection diagram of IEEE 24-bus system
假设位于母线18的输出功率为400 MW的发电机脱机是预想的整个系统中最严重的事故,针对此极限场景进行多目标储能配置,用本文的方法求得的多目标问题的帕累托前沿如图4所示。

表1 IEEE 24节点系统参数Table 1 Parameters of IEEE 24-bus System

图4 储能配置两目标优化模型的帕累托前沿Fig.4 Pareto frontier of bi-objective optimization model for energy storage configuration
由图4可知,采用本文方法求得的帕累托前沿分布均匀,具有较好的求解效果。通过模糊隶属度函数和熵权法[23],可以得到最优折中解。
为了验证本文所提多目标模型的有效性,将多目标模型所得的储能配置(方案1)与单目标模型结果对比。其中,仅优化目标函数1的储能配置为方案2,仅优化目标函数2的储能配置为方案3。具体结果如表2所示。
由表2可以看出,方案2配置的储能功率和能量容量最小,其所对应的储能配置成本目标值f1最小,然而此时系统的频率偏差平方的积分值f2最大;方案3配置的储能功率和能量容量最大,使得系统的频率偏差平方积分值最小,但是却使得储能配置成本最高。而在方案1中,由于同时考虑了成本和调频效果目标,可以在改善系统频率的同时降低储能的配置成本。3种配置方案对应的系统频率变化、系统频率变化率以及储能输出功率对比如图5—7所示。其中图5—7均通过将储能配置方案输入搭建的Simulink仿真模型进行仿真得到。
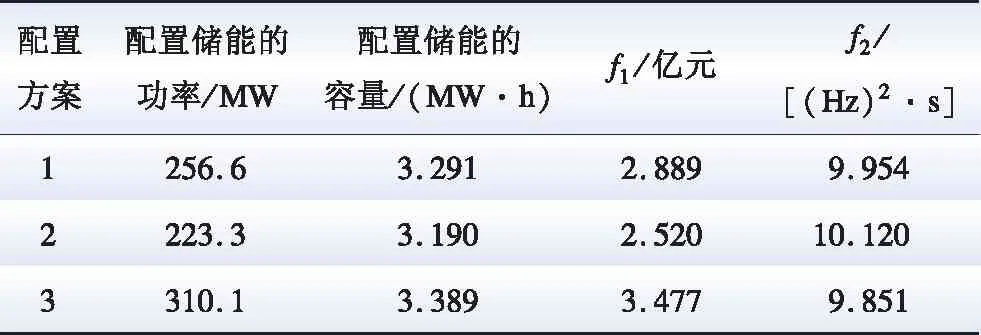
表2 3种储能配置方案比较Table 2 Comparison of three schemes for energy storage configuration
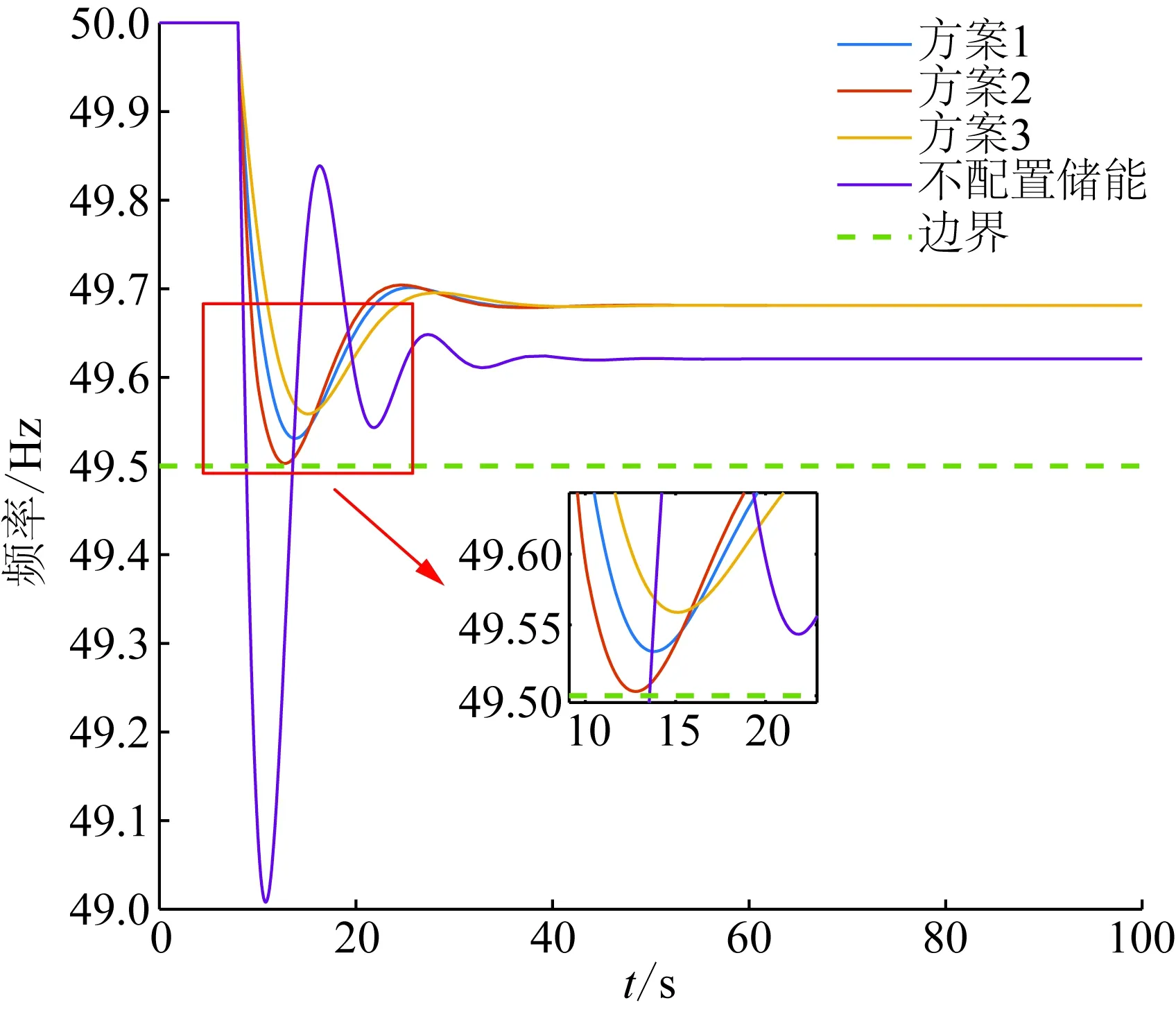
图5 3种配置方案的系统频率曲线Fig.5 System frequency response curves under three schemes for energy storage configuration

图6 3种配置方案的系统频率变化率曲线Fig.6 Curves of rate of frequency change under three schemes for energy storage configuration
从图5和图6可知,采用多目标优化得到的最优折中解,可以以更低的成本得到几乎与方案3配置一样的频率调节效果。与仅优化储能配置成本的配置方案2相比,方案2的系统频率最低点十分靠近低频减载的触发频率,而方案1的频率最低点则相对远离边界值,保持了一定的安全裕度,体现了多目标优化的效果。采用最优折中解配置方案,与不配置储能相比,频率最低点提升了0.55 Hz,频率变化率提升了0.4 Hz/s,起到了较好的配置效果。
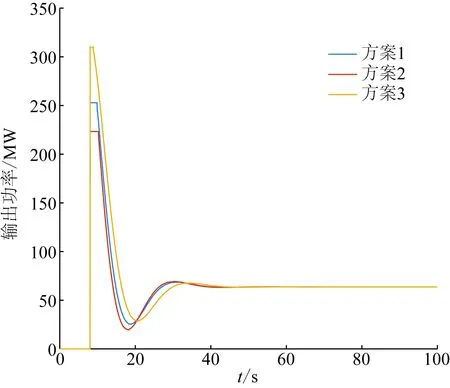
图7 3种配置方案的储能输出功率曲线Fig.7 Output power curves of energy storage under three configuration schemes
图8为储能配置方案1的SOC变化曲线。由于储能的初始SOC为0.8,仿真事故为脱机事故,需要储能系统注入功率,所以使得储能系统一直处于放电状态,SOC一直处于下降的状态。储能系统的SOC在0.2~0.8的区间内变化,满足了储能的安全运行需求。由此得知,经过多目标优化之后选取的最优折中解的方案1,既能保证系统遭遇严重事故时避免暂态低频减载的发生,又能保证储能运行在合理的范围之内。

图8 对应配置方案1的储能SOC变化曲线Fig.8 SOC curve under energy storage configuration scheme 1
为了验证所提方法的准确性,将求解多目标动态优化模型得到的系统频率变化曲线与将储能配置方案作为Simulink仿真系统参数得到频率仿真曲线进行对比,结果如图9所示。其中用于对比的方案为最优折中解的配置方案。

图9 采用仿真模型与计算模型得到频率变化曲线对比Fig.9 Comparison of system frequency-response curves from simulation and calculation model
从图9可以看出,采用仿真模型得到的系统频率变化曲线与采用多目标优化计算模型得到的频率变化曲线吻合的精度较高,验证了多目标动态优化计算模型的准确性。
5 结 论
本文基于电力系统等值频率响应模型提出了适合储能容量配置的具有分段函数约束的多目标动态优化模型,同时考虑了储能配置成本和暂态频率调节性能2个相互冲突的目标,重点解决了如何将其转化为多目标混合整数二次规划模型。
通过IEEE 24节点系统的仿真分析,结果表明,采用本文提出的储能容量配置多目标动态优化方法,在400 MW的发电机脱机时,通过配置255.3 MW/4.931 MW·h的储能后,频率最低点提升了0.55 Hz,频率变化率提升了0.4 Hz/s,在电网遭遇较大的事故时,可以有效地避免暂态低频减载的触发,并且保留了一定的暂态频率安全裕度,上述结果验证了所提多目标储能配置模型的有效性。
