促进间歇性可再生能源发电消纳的水电定价与能量管理策略

王一铮，李忠憓，黄晨宏，胡亦玺，郑真，马小丽，颜华敏，文福拴

(1.浙江大学电气工程学院，杭州市 310027；2.国网上海青浦供电公司，上海市 201700；3．浙江省能源业联合会，杭州市 310012)

0 引 言

可再生能源发电具有清洁、可持续的特征，系解决环境污染、气候变暖与化石能源枯竭等问题的重要途径[1-2]。近年来，我国的风电与光伏装机规模持续增大，利用水平不断提高。2019年，风电与光伏的发电量较上一年分别增长了10.9%和26.3%，占总发电量的比重已经分别达到了5.5%和3.1%[3]。风电与光伏发电是典型的间歇性可再生能源(intermittent renewable energy，IRE)，大量IRE发电的消纳通常需要与源[4-6]、荷[7]、储[8]、气[9]等进行协同配合。其中，水电站可依托河流或水库的库容能力，调节发电出力在日内的分布，来促进大量IRE发电的消纳。

在IRE与水电的协同调度方面，已有一些相关研究报道。文献[4]基于风电与光伏的随机出力时序模拟以及水电的短期优化调度，构建了水、火、风、光多类型能源的协调互补模型；文献[5]研究了大规模风电接入电网后的水电运行方式，以最大化间歇性可再生能源的发电量；文献[6]针对多能互补系统，从分系统与联合系统两个角度提出了适用于风、光、水互补特性的评价指标；文献[7-9]则分别研究了IRE发电与数据中心、储电设备和电气耦合设备的协同调度。

在现有研究中，水电的优化调度模型主要针对单一的决策主体。文献[10]研究了大、小水电站的短期协同调度，以电力系统整体的发电经济性最优与电力不足概率最小为优化目标；文献[11]研究了大规模水电系统的短期联合优化调度，分别考虑了给定时段内总弃水量最小、总调峰电量最大等优化目标；文献[12]研究了受端电网与水电站的协同优化调度，以受端的电负荷减去各水电站总出力后得到的净负荷水平最低为优化目标。

然而，在我国部分地区的小规模水电(小水电)的开发与利用中，往往涉及电网公司与水电站等多个独立的利益主体，水电的定价与能量管理也相互影响。部分地区针对小水电实行了固定电价、峰谷电价等多种水电定价与能量管理措施，但利益主体之间的互动性较差，往往存在以下问题：一是无法保障水电站的发电利润和电网公司的电能购买成本在合理水平；二是水电出力的时间分布不合理，影响了大量IRE发电的消纳。将博弈引入能源定价能量管理中，可以增加利益主体之间的互动性，保障各方利益。考虑多主体博弈的能量管理方法已有一些报道[13-16]，但鲜有涉及水电方面；在IRE发电与小水电站的协同调度方面也缺乏研究报道。

在上述背景下，本文针对小水电站的水电定价与能量管理策略开展研究，兼顾对IRE发电的消纳。首先，基于Stackelberg博弈提出水电定价与能量管理框架。接着，构建包含上层电网公司与下层水电站的双层优化决策模型。之后，将双层的非凸非线性问题转化为混合整数线性规划(mixed integer linear programming, MILP)问题, 并采用Yalmip/Gurobi求解器求解。最后，通过算例对所提方法进行验证。

1 水电定价与能量管理框架

首先针对包含小水电站和大量IRE发电的区域电力系统，构建水电定价与能量管理框架。水电站依靠河道或水库的库容能力，可在一定程度上灵活调节发电出力在日内的分布，与其他类型的电源进行协同互补，以促进对大量IRE发电的消纳。可按小水电站的调节特性将其分为统一调度水电站(coordinately-scheduled hydropower station, CHS)和自主调度水电站(independently-scheduled hydropower station，IHS)两类，如表1所示。其中，CHS由电力调控中心调度，并根据政府相关机构确定的固定电价对发电量进行结算。IHS则根据水电峰谷电价，自主调整日出力曲线，在水电电价较高时段多发电，以最大化发电收益。

表1 小水电站的分类与特点Table 1 Classification and characteristics of small hydropower stations

如图1所示，电力调控中心直接调度CHS，并在政府相关政策的约束下制定针对IHS的水电峰谷电价，确保各个IHS的平均水电电价在合理水平。通常可采用成本加成电价、受电市场倒推电价和标杆水电电价等作为参照。此外，电力调控中心还通过优化水电出力曲线，以提升消纳IRE发电的能力。IHS根据水电峰谷电价确定日出力曲线，对电价做出响应。在水电定价与能量管理过程中，电网公司在政府相关政策的约束下具有优先决策权，这样可构建基于Stackelberg博弈的双层优化决策模型，其中电网公司与IHS分别扮演领导者与追随者的角色。Stackelberg博弈与经典博弈有所不同：在Stackelberg博弈中，局中人并非同时做出决策，而是先由领导者决策，接着追随者对领导者的决策做出最优响应，之后领导者再根据追随者的响应做出最优决策，如此循环，直至获得均衡状态。

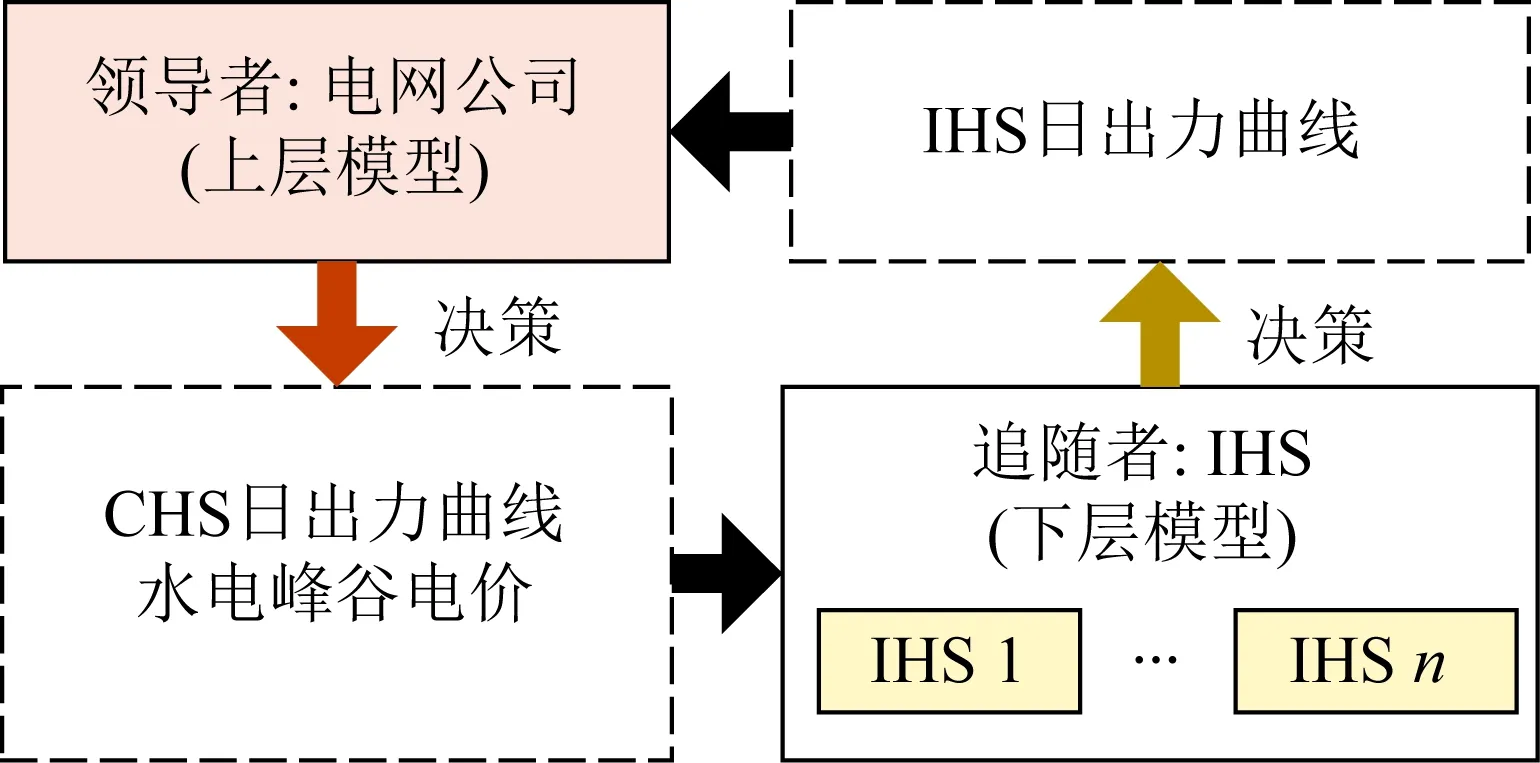
图1 基于Stackelberg博弈的水电定价与能量管理框架Fig.1 Framework of hydropower pricing and energy management based on the Stackelberg game

2 水电定价与能量管理的决策模型

2.1 上层电网公司的决策模型

2.1.1目标函数

假定在区域电力系统中包括CHS、IHS以及容量较大的光伏发电站(photovoltaic station, PVS)和风力发电站(wind power station, WPS)。在决策模型的上层，电网公司以弃风弃光量u11与CHS的弃水量u12的加权和最小为优化目标，可描述为：

minu1=τ1u11+τ2u12

(1)

其中：

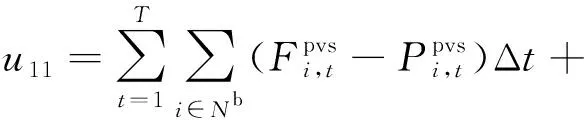
(2)

(3)

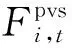
2.1.2约束条件

1)电功率平衡约束。

节点功率平衡约束:

(4)

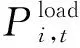
其中：

(5)

(6)

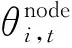
2)PVS与WPS发电机组出力约束：

(7)

(8)

3)外部电网输入/输出功率约束：

(9)

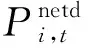
4)水电电价约束。

这里以水电标杆电价作为基准，来确定电网公司购买水电的平均电价水平适当。水电峰谷电价中包含峰值与谷值，如式(10)所示。电网公司从每个IHS购买电能的价格不能过多高于或低于水电标杆电价，如式(11)所示：

(10)

(11)

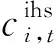
水电峰谷电价的每段峰值与谷值都需要持续一定的时间，即存在最小值，式(12)和式(13)分别表示水电峰谷电价的每段峰值与谷值的持续时间约束：

(12)

(13)

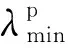
5)CHS发电机组出力约束。

CHS发电机组的出力受调度周期内计划发电量和装机容量的约束，分别如式(14)和(15)所示；发电机组存在爬坡(滑坡)速度约束，如式(16)所示；发电机组需要满足最小开机/停机持续时间约束，如式(17)和(18)所示：

(14)

(15)

(16)

(17)

(18)

2.2 下层IHS的决策模型

2.2.1目标函数

在下层模型中，每个IHS均为决策主体，分别独立地针对电网公司的决策进行最优响应，目标为最大化发电收益。实际运行数据表明，IHS的出力曲线可近似用若干段水平线来表示，且IHS通常尽可能减少出力调节，以降低人工成本和运行维护成本。假定IHS的人工成本与运行维护成本中的可变部分与其出力调节幅度有关，则IHS的目标函数可描述为：

(19)

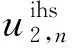
2.2.2约束条件

1)IHS出力约束。

IHS的发电功率受装机容量约束，如式(20)所示；IHS存在爬坡(滑坡)速度约束，如式(21)所示：

(20)

(21)

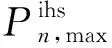
2)IHS出力调节约束。

IHS的最大发电出力与单位时间通过的水流量有关，考虑到弃水现象，其发电出力需满足式(22)所描述的约束。将单位时间内的上游来水量与通过水流量之差定义为“拦水量”，则IHS当日的累计拦水量可由式(23)描述。IHS的上游水位与其累计拦水量有关：累计拦水量过大会导致水电站的上游水位上升，累计拦水量过小(可为负值)则导致水电站的上游水位下降，带来安全与生态影响。因此，IHS拦水量的调节范围有限，如式(24)所示：

(22)

(23)

(24)

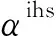
2.3 模型的转化与求解

在由式(1)—(24)构成的双层优化问题中，式(11)中包含变量的乘积项，式(19)中包含绝对值项，这样其为非线性优化模型。为提高求解效率，对模型进行线性化处理，并将双层优化问题转化为单层优化问题。

2.3.1下层目标函数的线性化

对于式(19)中的绝对值项，可引入两个非负的辅助变量进行线性化处理，将式(19)改写为：

(25)

需要增加以下约束：

(26)

dn,t≥0

(27)

en,t≥0

(28)

式中：dn,t和en,t均为非负的辅助变量。

2.3.2双层优化问题的转化

如图2所示，上层电网公司的优化决策问题与下层IHS的优化决策问题构成了双层优化问题。在基于Stackelberg博弈的双层优化问题中，可应用KKT条件等效替代下层的IHS优化决策问题，并将所得到的线性化KKT条件[17]作为上层问题的附加约束，从而实现双层优化问题向单层优化问题的转化。

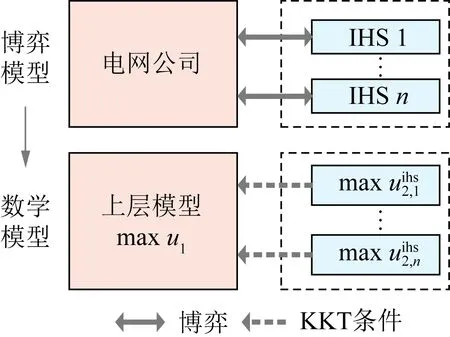
图2 水电定价与能量管理的博弈模型及其数学模型Fig.2 Gaming model and mathematic model of the hydropower pricing and energy management

下层问题的拉格朗日函数如式(29)所示，所得到的线性化KKT条件如式(30)所示，具体可表示为附录A中的式(A2)—(A32):

(29)

(30)

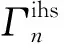
2.3.3上层约束条件的线性化

对于式(11)中的变量乘积项，可采用强对偶理论[18]得到附录A中的式(A33)，进而将式(11)改写为式(31)所示的线性形式：

(31)

2.3.4问题求解

至此，所构造的双层非凸非线性优化问题就转化为式(32)所描述的MILP问题，可在Matlab环境中采用商业求解器Yalmip/Gurobi求解，如此得到的最优解即为博弈的均衡点。

(32)

3 算例与结果

3.1 参数设置

以IEEE 9节点标准电力系统为基础，构建了图3所示的算例系统。在该系统中，有多座小水电站和较大容量的PVS，电力负荷水平较低，消纳IRE发电与清洁电能外送都有一定的困难。外部电网通过节点1与该系统连接；IHS 1、IHS 2和IHS 3分别与节点1、2和3相连，CHS与节点2相连，PVS与节点8相连；节点5、7和9是电力负荷节点。水电站与PVS的相关参数分别如附录B中的表B1和图B1所示，电力负荷与电网输入/输出功率上限如附录B中的图B2所示，其他参数如附录B中的表B2所示。下面针对如下4个场景进行分析：

场景1：小水电站处于丰水期，IHS的发电量按水电峰谷电价结算。

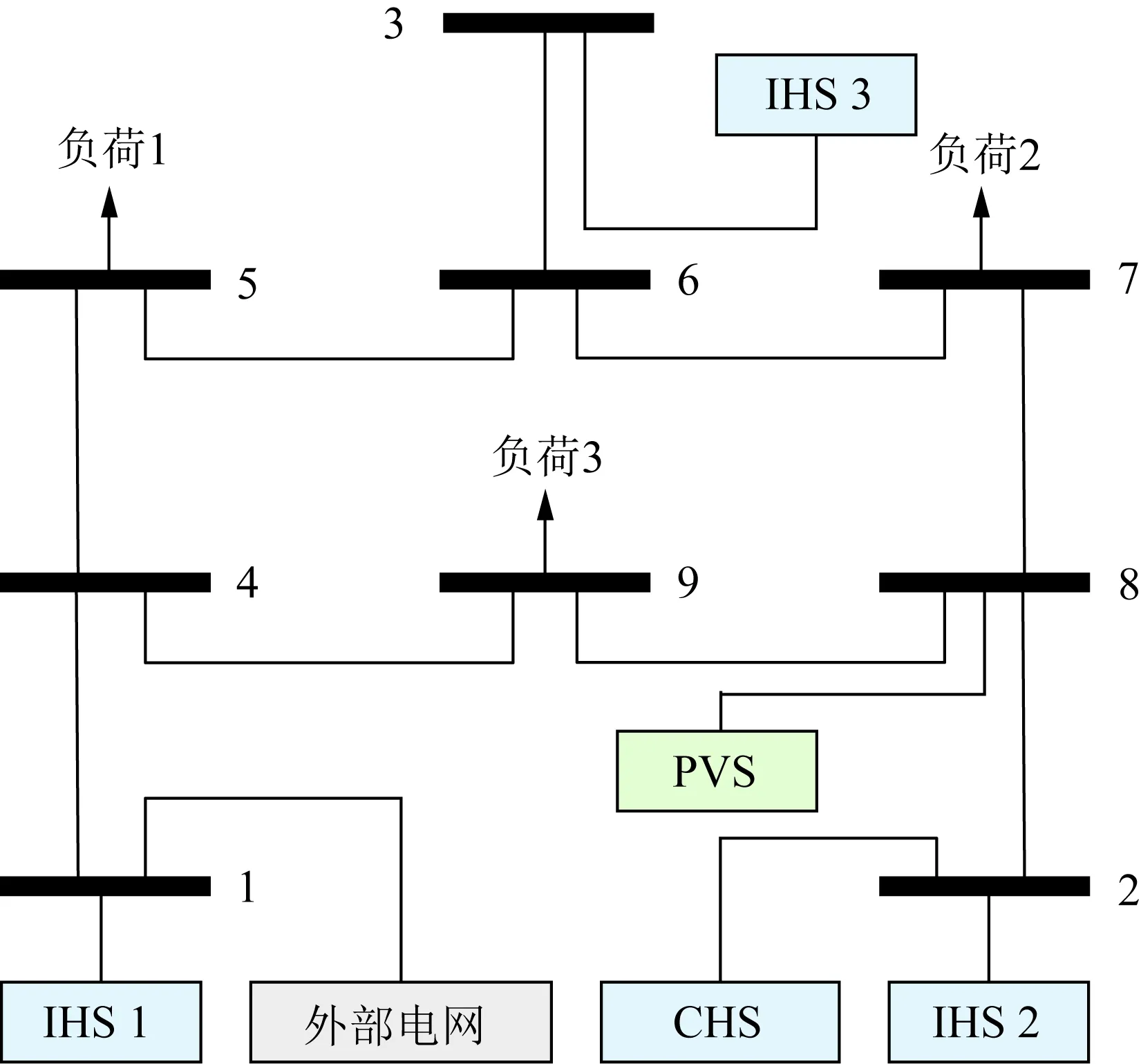
图3 算例系统Fig.3 A sample power system

场景2：小水电站处于枯水期，IHS的发电量按水电峰谷电价结算。

场景3：小水电站处于丰水期，IHS在日内均匀出力，其发电量按水电标杆电价结算。

场景4：小水电站处于枯水期，IHS在日内均匀出力，其发电量按水电标杆电价结算。

3.2 结果与分析

3.2.1水电电价与水电站出力分析

3个IHS在场景1和2的水电峰谷电价如图4所示，在4个场景下各发电厂/站的日发电出力曲线、与外部电网的日输入/输出功率曲线、日总负荷曲线如图5所示。在场景1和2中，电网公司针对3个IHS分别制定了水电峰谷电价；IHS对电价做出响应，在电价峰值时段提高机组出力，在电价谷值时段降低机组出力或直接停机，以此最大化发电收益。CHS则受电力调控中心直接调度，根据系统运行需要灵活调整发电出力。引入水电峰谷电价也影响对CHS的优化调度：相较于场景3和4，在场景1和2中CHS出力调节幅度较小，这是因为IHS的出力具有灵活性，可满足系统部分调峰需求。

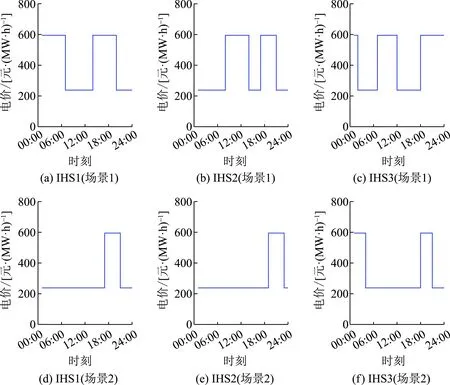
图4 3个IHS在2种场景中的水电峰谷电价Fig.4 Peak-valley prices of hydropower of 3 IHSs in two scenarios

在场景1中3个IHS的水电电价峰值时长分别为12、10和12 h；在场景2中3个IHS的水电电价峰值时长分别为3、3和4 h。在场景1和2中，电价峰值时长相差较大，这一方面是由于IHS在丰水期的调度时期内可调节发电量较大，可通过设置多个峰价时段来引导IHS灵活调整出力；另一方面则是因为差异化的峰值时长能保证电网公司的电能购买成本处于合理水平。如表2所示，电网公司从IHS 1、IHS 2和IHS 3购买电能的平均价格与标杆水电电价的偏差均在允许范围内。

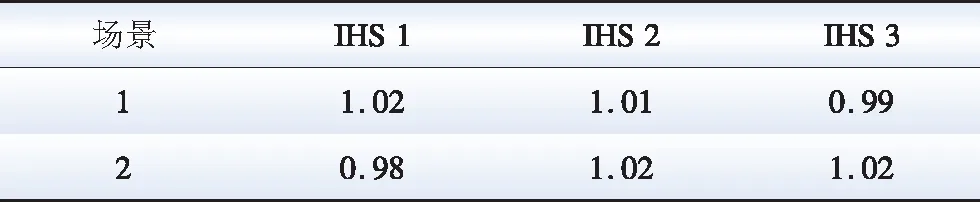
表2 两种场景中的水电平均电价与水电标杆电价的比值Table 2 Ratios of average hydropower prices to the benchmark hydropower price in two scenarios

3.2.2光伏发电消纳分析

图5展示了4种场景中的小水电站发电出力与PVS出力。在场景1中，IHS 2、IHS 3和CHS在光伏发电的峰值时段 (11:00—16:00)均降低了发电出力，为消纳光伏发电提供了空间。在场景3中，CHS在14:00—16:00时段内降低了发电出力，促进了对光伏发电的消纳。在场景2与4中，由于处于枯水期， PVS与水电站的日出力曲线均呈现出“峰谷交错”的特征，光伏发电被全部消纳。

如表3所示，场景1的弃光率远小于场景3，这是由于3个IHS在水电峰谷电价引导下进行有序发电，实现了水电与光伏两种发电资源的协调互补。而在场景2与4中，光伏发电被系统全部消纳，这是因为水电站在枯水期的日发电量较小，故而可以更为灵活地在日内调整发电出力，为消纳光伏发电提供了较为充分的空间。

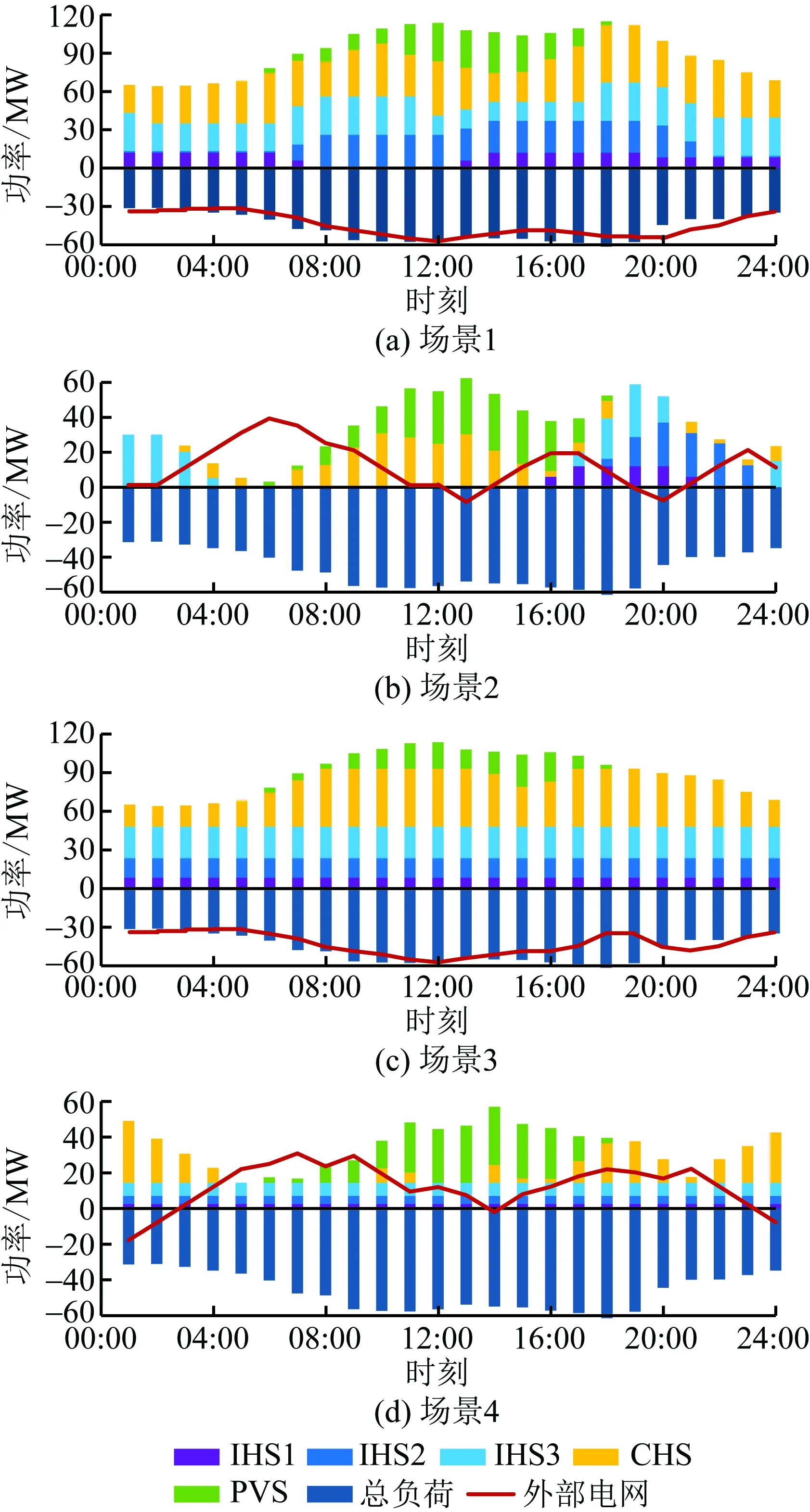
图5 4种场景中的小水电站发电出力与PVS出力Fig.5 Power outputs of small hydropower stations and PVSs in four scenarios

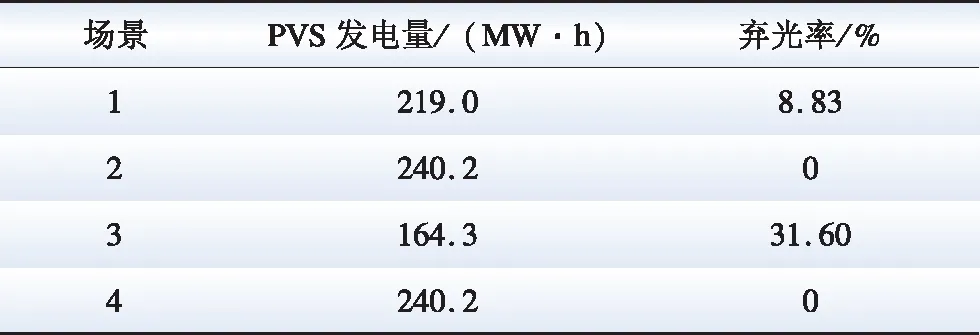
表3 4种场景中的光伏发电消纳情况Table 3 Accommodation status of photovoltaic power generation in 4 scenarios

3.3 敏感性分析

现在对所构建模型的敏感性进行分析。逐次调整PVS的装机容量，分析在现有水电资源条件下区域电力系统消纳IRE发电的能力。如图6 (a)所示，随着PVS装机容量的提高，丰水期的弃光率逐渐增加,且场景1的弃光率始终低于场景3，而枯水期的弃光率仍旧保持在较低水平。可以看出，在水电峰谷电价引导下，IHS可提高电力系统的运行灵活性，在保证电网公司与水电站利益的同时，促进对IRE发电的消纳；与此同时，IRE发电的开发与利用需要综合考虑区域内已有的水电等其他类型电源的发电出力情况。

现在分析水电站来水量对区域电力系统消纳IRE发电的影响。如图6 (b)所示，随着水电站来水量的增大，丰水期的弃光率逐渐增大，这是因为随着水电出力的增加，光伏发电的消纳空间减小。此外，场景1与3的弃光率逐渐接近，这是因为较大的来水量降低了IHS发电出力的灵活性，从而削弱了水电峰谷电价对IHS的引导作用。

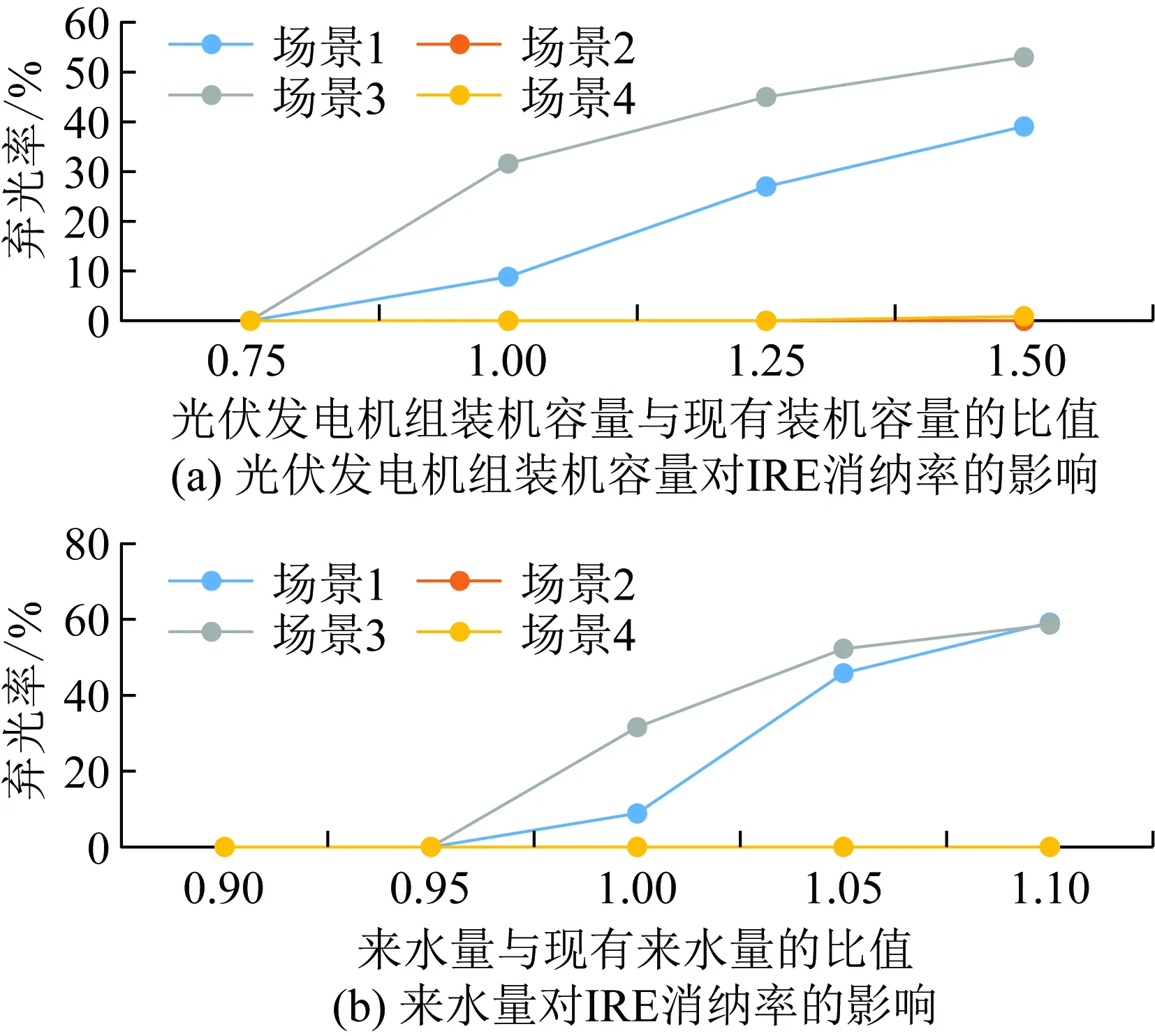
图6 所构建模型的敏感性分析Fig.6 Sensitivity analysis of the presented model

4 结 语

针对IRE发电的消纳问题，提出了一种考虑多主体博弈的水电定价与能量管理策略。在Stackelberg博弈的框架下，构建了包含上层电网公司与下层水电站的非凸非线性双层优化决策模型：上层的决策目标是弃风弃光量与弃水量的加权和最小，下层的决策目标则是IHS的发电收益最大。之后，将该非凸非线性双层优化问题转化为MILP问题并采用Yalmip/Gurobi求解器求解，其最优解即为Stackelberg博弈的均衡点。对算例系统的仿真结果表明，由电力调控中心直接调度的CHS和由水电峰谷电价引导的IHS均可增强电力系统的运行灵活性；应用所提出的水电定价与能量管理策略，能够保障电网公司与水电站的合理利益，促进IRE发电的开发与利用。

本文从水电定价角度探究了水电能量管理策略，在后续研究中将考虑水电参与辅助服务市场的运营策略等问题。