弱电网下负序控制对变流器并网系统稳定性影响分析

2021-03-18李丹丹张爱军袁辉邢华栋甘青山辛焕海

电力建设 2021年3期

李丹丹，张爱军，袁辉，邢华栋，甘青山，辛焕海

(1.内蒙古电力(集团)有限责任公司内蒙古电力科学研究院，呼和浩特市 010020；2. 浙江大学电气工程学院，杭州市 310027)

0 引言

随着电力电子技术的快速发展以及国家大力推动清洁能源建设，风电、光伏等以变流器为接口的发电装备在电网中占比逐渐增高，新能源接入的局部电网呈现弱电网趋势(本文针对低短路比电网)[1-3]。此外，由于三相系统中单相负荷分配不均衡、不对称故障等原因，电网往往存在三相电压不平衡问题[4]。并网点电压不平衡会引起基于锁相环(phase locked loop，PLL)矢量控制的变流器出现功率波动和电流畸变等问题，该问题在弱电网中更加突出[5-6]。

为改善并网变流器输出功率/电流质量，国内外关于不平衡电网下变流器的控制设计已取得不少研究成果[7-16]。早期有学者提出采用正反转同步坐标系双电流环PI控制，可以同时实现对正负序分量的无差调节[7-9]。然而，该控制一方面由于陷波器的引入会导致相位延时，进而影响动态性能；另一方面，由于新增了反转同步坐标系电流环，控制实现较为复杂[10]。为避免双同步坐标系双电流环控制的缺陷，文献[11-13]提出在原有电流内环PI控制上并联(准)谐振控制器(即比例积分-(准)谐振控制)实现负序电流的无差调节，该控制无需陷波器和附加反转同步坐标系电流环控制，控制结构相对简单、易于实现。此外，也有学者提出基于静止坐标系的负序控制[14]、模型预测控制[15]、内模控制[16]等。

以上文献主要集中于负序控制设计，而负序控制作为一种附加控制，不可避免改变了变流器原有针对平衡电网下设计的基于锁相环矢量控制结构，从而影响变流器并网系统控制性能和稳定性。文献[5]指出为实现正、负序分离而嵌入的陷波器，会恶化电流环的动态性能，此外在不对称故障发生和消失的过程中变流器可能会失稳，然而文中仅通过仿真说明，没有详细解释失稳机理。文献[17]指出谐振系数增大，会恶化转子电流动态性能。然而，上述文献较少关注负序控制如何影响变流器并网系统稳定性。

广义阻抗法是基于频域理论的阻抗分析法的一种[18]。该类分析方法通过测量得到变流器和电网的外特性，进而定量分析系统的稳定性，其优势在于分析过程中无须知道变流器的详细控制参数。研究表明，广义阻抗法可将变流器并网系统从一个多输入多输出系统问题转化为单输入单输出系统问题，进而基于Nyquist判据可对原系统进行定量稳定性分析。此外，与传统阻抗分析法相比，广义阻抗法具有一定的优势：相较于正负序阻抗分析法，广义阻抗法考虑了阻抗矩阵中的非对角元素项，理论依据更严格；相较于基于广义Nyquist判据的dq阻抗法，其能够将系统振荡问题解释为电路的串并联谐振问题，具有一定的物理意义。此外，文献[19]进一步探讨了广义阻抗的物理意义，提出了原-对偶复电路的概念。原-对偶复电路与实际物理系统具有对应关系，能够解释广义阻抗的物理意义。

本文针对平衡弱电网下变流器并网系统稳定性问题，以比例积分-准谐振(proportional-integrational quasi-resonant，PIR)控制器(下文中提到的负序控制都特指PIR控制策略)为例，研究负序控制策略带来的结构改变对平衡电网下系统稳定性的影响。首先，对负序控制策略进行介绍，并在系统极坐标系中建立平衡电网中考虑负序控制策略影响的变流器并网系统幅相阻抗模型以及原-对偶复电路。其次，通过分析负序控制策略对变流器侧导纳矩阵元素的影响，判断负序控制策略可能对系统稳定性的影响；采用广义阻抗判据进一步分析负序控制策略如何影响系统稳定性，并采用特征值分析，验证上述分析结果。研究表明，负序控制策略设计不当可能会引发次同步和100 Hz频率附近稳定问题。最后，通过时域仿真验证理论分析的正确性。

1 不平衡电网下并网变流器PIR控制策略

图1给出单变流器并网系统单线框图、PIR控制结构以及考虑负序控制前基于锁相环的矢量控制(这里有功外环控制特指直流电压控制)[12]。其中，Udc、Usabc、Uabc、Eabc分别为直流电压、变流器端口三相电压、变流器三相端电压、无穷大电源电压；下标d(d+)、q(q+)分别表示正旋转坐标系下d轴和q轴分量；下标d-、q-分别表示反旋转坐标系下d轴和q轴分量；上标n、p分别表示负序和正序分量；上标ref表示参考指令；Lf、Cf为滤波电感、电容；L1表示线路电感。

电网电压不平衡时，不考虑零序分量，标幺值下变流器网侧输出复功率S可表示为：

(1)

式中：上标“∧”表示共轭；ω为电网频率；Udq+=Ud++jUq+，Idq+=Id++jIq+；e表示自然常数。

将式(1)展开，瞬时有功及无功功率表达式为：

(2)

式中：P0、Q0分别为瞬时有功、无功功率的直流分量；Pc2、Ps2和Qc2、Qs2分别代表有功功率和无功功率的2倍频分量幅值。

(3)

由式(2)可知，电网电压不平衡时变流器输出功率出现2倍频波动，进而会引发直流电压出现2倍频波动和并网电流发生畸变。

本文所介绍并网变流器PIR控制策略控制目标为抑制网侧有功功率2倍频波动，该控制目标在负序控制策略设计中较常见[12]。由图1可知，PIR控制策略根据测量得到的有功功率P(包括P0、Pc2、Ps2)、无功功率Q(包括Q0、Qc2、Qs2)计算正负序dq轴电流分量参考值，基于正序电流内环PIR控制，实现有功功率2倍频波动抑制。受篇幅所限，这里不详细介绍电流参考值推导过程，具体可参考文献[12]。当无功功率参考值为0时，电流参考值具体表达式为：

图1 基于PIR控制的变流器并网系统Fig.1 The one-line diagram of grid-connected inverter with PIR controller

(4)

由图1可知，除去正负序电流参考指令计算环节，并网变流器PIR控制策略在原有基于锁相环的矢量控制基础上，主要做了两方面改进：1)正负序分量分离；2)准谐振控制器的引入。

1.1 解耦双同步旋转坐标系锁相环

不平衡电网下，实现负序控制首要解决的问题是如何快速准确地提取正负序分量，这需要有动态性能良好的锁相环技术。解耦双同步旋转坐标系(decoupled double synchronous reference frame，DDSRF)锁相环采用正负序双同步坐标系结构，能够精确分离不平衡电网下正负序分量，是一种较常用的适用于不平衡电网下的锁相技术，具体控制结构如图2所示[12,20]。

考虑电网电压不平衡，变流器端电压表示为：

(5)

式中：Ua、Ub、Uc分别为变流器a、b、c三相端电压分量；φ为端电压初始相角。

图2 基于解耦双同步旋转坐标系锁相环Fig.2 Diagram of PLL based on decoupled double synchronous reference frame

(6)

(7)

1.2 准谐振控制器

为实现电流参考指令的无差调节，电流内环需要对正序直流分量和负序2倍频电流分量同时进行无静差控制。然而，PI控制仅能实现直流电流分量无差调节。准谐振控制器仅在指定频率处一定频带内表现较大增益，其余频段增益近似为0，故可实现特定频率交流量的精确跟踪。为此，电流内环在原有PI控制环节并联准谐振控制器，实现2倍基频负序电流无差调节。准谐振控制器传递函数Gqr(s)为：

(8)

式中：Kr为谐振系数；ω2为谐振频率，即2倍频电网频率；ωc为截止角频率，本文取10 rad/s。

2 平衡电网下考虑负序控制系统数学模型

本节构建了平衡电网下考虑负序控制的变流器系统数学模型。首先，推导了平衡电网下考虑负序控制策略的变流器侧幅相阻抗模型，并与考虑负序控制前变流器幅相阻抗模型对比，说明负序控制对变流器侧幅相阻抗模型中导纳元素的改变；其次，介绍电网侧幅相阻抗模型；最后，构建考虑负序控制变流器并网系统原-对偶复电路。

2.1 变流器侧幅相阻抗模型

观察图1和图2可知，变流器的负序控制策略对变流器侧动态主要有两部分的改变：1)电流内环d轴和q轴分量参考指令；2)电流内环PI环节动态。

2.1.1电流d轴和q轴参考指令

(9)

式中：Glp(s)=1/(1+T2s)为低通滤波环节，T2为时间常数。

结合式(4)和(9)可得，正负序电流d轴和q轴参考指令表示为：

(10)

其中，P0根据图1可表示为：

P0=Udc(Udc-Udcref)Gdc(s)

(11)

式中：Udcref为直流电容电压参考值；Gdc(s)=kdcp+kdci/s为直流电压外环传递函数，kdcp、kdci分别为比例系数和积分系数。

因此，变流器电流d轴和q轴参考指令为：

(12)

2.1.2电流内环PI环节动态

由图1可知，电流内环PI环节(Gi(s))变为比例积分-准谐振环节(G′i(s))，即

G′i(s)=Gi(s)+Gqr(s)

(13)

式中：Gi(s)=kip+kii/s为电流内环传递函数，kip、kii分别为比例系数和积分系数。

变流器侧其余部分动态参考附录A。线性化变流器侧动态模型，可求得考虑负序控制后变流器侧幅相阻抗模型：

(14)

(15)

式中：下标“0”表示稳态值，这里规定电流以流向变流器方向为正方向；Yg11n(s)和Yg22n(s)为变流器侧幅相阻抗矩阵中导纳元素，详细推导请参考附录A。

此外，不考虑负序控制时变流器侧幅相阻抗模型的形式与式(14)相同，其中对角导纳元素Yg11(s)和Yg22(s)的具体表达式为：

(16)

式(16)的具体推导参考附录A。

对比Yg11n(s)和Yg11(s)、Yg22n(s)和Yg22(s)可知，负序控制带来的控制结构改变影响了幅相导纳元素Yg11(s)和Yg22(s)的动态。此外，负序控制策略带来的结构改变可以看成是对变流器侧幅相阻抗模型的摄动，即考虑负序控制时变流器侧幅相阻抗模型表示为：

(17)

(18)

2.2 变流器原-对偶复电路

基于2.1节变流器侧幅相阻抗模型，复空间下设备侧复电路形式可表示为：

(19)

(20)

(21)

(22)

式中：为表述方便，偏差量“Δ”以及代表导纳动态的“(s)”已省略；U、I分别表示电压和电流振荡分量；下标P和D分别表示原分量和对偶分量；Ye1n_VSC、Ye2n_VSC、Ye3n_VSC分别为考虑负序控制影响后设备侧动态构成的广义导纳；Ye1_VSC、Ye2_VSC、Ye3_VSC分别为考虑负序控制前设备侧广义导纳；Δ1、Δ2、Δ3表示负序控制对各个设备侧广义导纳的摄动，具体推导参考附录A。

电网侧复电路可表示为[19]：

(23)

式中：E为扰动电压的振荡分量，本文不考虑外部扰动源的影响，故后续分析时认为ΔEP=0，ΔED=0；Ye2_L、Ye3_L、Ye2_C、Ye3_C为网络侧广义导纳。

(24)

(25)

(26)

图3给出考虑负序控制影响的并网变流器系统原-对偶复电路框图。从复电路的角度可以看出，负序控制带来的结构改变可看成是对各个设备侧广义导纳的摄动。

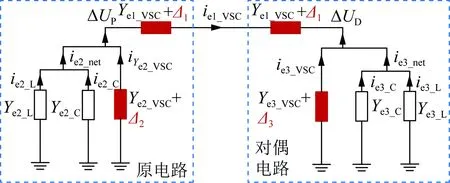
图3 系统的等效原-对偶复电路Fig.3 Primal-dual complex circuit of the system

3 负序控制对系统稳定性的影响

本节分析了负序控制带来的结构改变对变流器并网系统稳定性的影响。首先，分析了负序控制对设备侧幅相导纳的影响，判断负序控制如何影响系统稳定性；其次，基于广义阻抗判据分析了负序控制对变流器并网系统稳定性的影响，并采用特征值分析验证分析结果的有效性。另外，从复电路的角度解释了变流器并网系统失稳振荡机理。

3.1 负序控制对设备侧导纳元素的影响

为反映负序控制对设备侧幅相阻抗模型中导纳元素Yg11和Yg22的影响，图4给出考虑负序控制前后Yg11和Yg22的Bode图。由图4可知，负序控制的影响主要有2种情况：情况1，主要影响了Yg11次同步频段的幅值和相角，以及Yg22在次同步频段表现的幅值；情况2，主要影响了Yg11和Yg22在100 Hz附近的幅值和相角。这说明负序控制主要影响变流器并网系统次同步频段以及100 Hz频率附近的稳定性，当变流器并网系统在这2种情况下表现为弱阻尼时，负序控制带来的结构改变可能会使系统存在失稳风险。

进一步地，由图4可得出结论：情况1主要与电流内环参考值动态的改变有关，情况2主要与准谐振控制器动态有关。由图4可知，随着谐振系数的增加，负序控制对情况1的影响基本不变，对情况2的影响越来越大，特别地当Kr=0(即不考虑准谐振控制器)时，负序控制影响情况2很小。这说明准谐振控制器主要影响情况2，对情况1基本不影响。另外，根据第2节的分析可知，负序控制对原有控制结构的改变主要有2个部分：1)电流内环参考值动态的改变；2)准谐振控制器的引入。故情况1主要是由于负序控制对电流内环参考值动态的改变造成的。

3.2节将进一步基于广义阻抗判据和特征值分析研究负序控制对变流器并网系统稳定性的影响。这里主要对系统存在次同步或100 Hz左右弱阻尼这2种场景进行讨论。

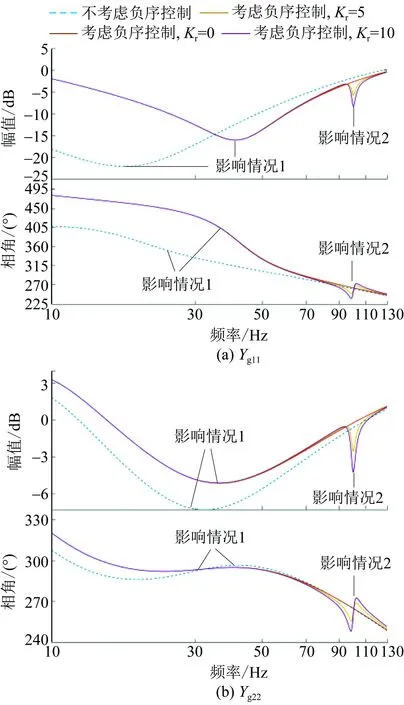
图4 考虑PIR控制前后变流器侧Yg11和Yg22的Bode图Fig.4 Bode plot of Yg11 and Yg22 when considering PIR control or not

3.2 负序控制对系统稳定性影响

变流器并网系统闭环特征方程可转化为：

1+ZG_grid/ZG_VSC=0

(27)

式中：ZG_grid/ZG_VSC为系统开环传递函数，具体推导参考附录B。

根据广义阻抗判据可知[18]，当ZG_grid/ZG_VSC的Nyquist曲线不包围(-1, 0)点时，系统是稳定的，反之，系统不稳定。

结合上文分析可知，负序控制带来的结构改变主要影响系统次同步或100 Hz附近系统的稳定性。因此，本节将基于系统存在次同步或100 Hz附近这2种弱阻尼模态场景，分别分析负序控制带来的电流内环参考指令和PI控制环节两者动态改变对系统稳定性的影响，2种场景下变流器并网系统的参数和最弱特征根变化如表1和表2所示。2种场景下考虑PIR前后系统开环传递函数Nyquist图如图5、6所示。

表1 变流器并网系统的参数Table 1 Parameters of the grid-connected converter

表2 变流器并网系统最弱特征根Table 2 Weakest eigenvalue for different cases

图5 场景1下考虑PIR前后系统开环传递函数Nyquist图Fig.5 Nyquist plot of the system’s open-loop transfer function for case 1 when considering PIR control or not

1)场景1：系统存在次同步弱阻尼模态。

由图5可知，考虑负序控制前后，系统Nyquist曲线由不包围(-1, 0)点变为包围(-1, 0)点，说明负序控制恶化了系统稳定性，此外，随着Kr的增大，Nyquist曲线变化不大，这说明系统稳定性恶化与准谐振控制器的引入关系不大，即因负序控制带来的电流参考指令改变恶化了系统稳定性。由表2可知，考虑负序控制前后系统最弱特征根由稳定变为不稳定(振荡频率在8 Hz左右)且当Kr由0增大到5时，系统最弱特征根基本不变，特征根计算结果与Nyquist曲线分析结论一致，说明了理论分析的有效性。此外，通过计算发现Yg11n(j 53.303)≈0，结合图3，从复电路的角度可以得出结论：考虑负序控制后(即在Δ1、Δ2、Δ3的摄动下)，系统在次同步频段更容易出现图7(a)所示串联电路谐振。

图6 场景2下考虑PIR前后系统开环传递函数Nyquist图Fig.6 Nyquist plot of the system’s open-loop transfer function for case 2 when considering PIR control or not

图7 特殊频段下系统谐振时等效原-对偶复电路Fig.7 Primal-dual complex circuit for system resonance in special frequency band

2)场景2：系统存在100 Hz附近弱阻尼模态。

由图6可知，当考虑负序控制时，系统Nyquist曲线向左移动，这说明负序控制引入会恶化系统稳定性，此外，当准谐振控制器增益系数Kr由5变化到10时，系统Nyquist曲线由不包围(-1, 0)点变为包围-1, 0)点，说明随着准谐振控制器增益系数Kr的增大，系统稳定性会进一步恶化。由表2中场景2最弱特征根结果可知，随着负序控制引入系统稳定性变差，且当Kr由5增大到10时，系统由稳定变为不稳定(振荡频率100 Hz左右)，最弱特征根对比结果与Nyquist曲线分析结论一致。此外，由于Ye1_VSC(j 694.30)≈0(即Yg11n(j 694.30)≈Yg22n(j694.30))，结合图3从复电路的角度可得结论：考虑负序控制后，可能会使系统出现图7(b)所示并联谐振。

综上可知，负序控制导致的电流参考值动态的改变和准谐振控制器环节的增加会使变流器并网系统存在次同步以及100 Hz附近的失稳风险。更进一步地，准谐振控制器增益系数的增加会进一步恶化100 Hz附近的系统稳定性。

4 仿真验证

为进一步验证上述分析结果，基于MATLAB/ Simulink环境搭建了图1所示系统的电磁暂态模型，控制参数如表1所示。首先，基于不平衡电网，验证负序控制策略的有效性；其次，基于平衡电网，验证上述关于负序控制对系统稳定性影响结论的有效性。

4.1 不平衡电网中负序控制策略有效性验证

该负序控制策略采用PIR控制，以抑制网侧有功功率2倍频波动为目标。当t=2 s时，A相电网电压下降到50%，B、C相电压保持不变。电网三相电压和变流器输出有功功率如图8所示。

由图8可知，对比加入负序控制前后，变流器输出有功功率波动得到有效抑制，验证了PIR控制策略的有效性。

图8 不平衡电网电压下有功功率对照Fig.8 The comparison of active power under unbalanced grid voltage

4.2 负序控制对系统稳定性影响验证

图9、图10分别为场景1和场景2数字仿真结果。考虑场景1时，刚开始变流器不考虑负序控制，t=1.00 s时，电网电压发生0.01 pu跌落，0.01 s后电压恢复，t=5.00 s时，变流器切换到负序控制策略(考虑到Kr数值变化对次同步频段稳定性影响较小，这里仅以Kr=0为例给出相应仿真结果)。由图9可知，当控制策略由不考虑负序控制切换到考虑负序控制时，变流器输出电流波形由收敛变为发散，且振荡频率在8 Hz左右，说明负序控制可能会恶化系统稳定性。

图9 场景1变流器输出电流波形Fig.9 Current output of the converter in case 1

图10 场景2变流器输出电流波形Fig.10 Current output of the converter in case 2

考虑场景2时，刚开始变流器不考虑负序控制，t=1.00 s时，电网电压发生0.01 pu跌落，0.01 s后电压恢复，t=3.00 s时，切换到负序控制策略Kr=5.0且电网电压发生0.01 pu跌落，0.01 s后电压恢复，t=5.00 s时，Kr增大到10。由图10可知，随着负序控制的接入，系统输出电流收敛速度变慢，且当Kr=10时，系统输出电流波形发散且振荡频率在100 Hz左右，说明负序控制可能会恶化100 Hz附近系统稳定性，且增益系数越大，系统越有可能发生100 Hz振荡。综上所述，仿真分析结果与3.2节理论分析结论一致。