基于深度Q学习的电热综合能源系统能量管理
2021-03-18王新迎赵琦赵黎媛杨挺
王新迎,赵琦,赵黎媛,杨挺
(1.中国电力科学研究院有限公司,北京市 100192;2.天津大学电气自动化与信息工程学院,天津市 300072)
0 引 言
随着社会的不断发展进步,人类对于能源的需求不断增大,而石油、煤炭等传统化石能源日渐枯竭,发展环境友好的可再生能源、提高能源利用效率是当今世界共同关注的焦点。综合能源系统(integrated energy system, IES)可实现能源的梯级利用以及多种能源的协调互补,是缓解环境压力的重要选择[1-2]。在能源需求中,电能与热能是人类生活的基本能源需求,也是综合能源系统的两大主要能源形式[3]。电热综合能源系统并非2个独立供能系统的直接叠加,而是通过对多种能量单元的协同管理,在更大范围内实现系统资源的优化配置。
多种能量单元的共存和使用使得如何对电热综合能源系统进行能量管理以实现系统的运行优化得到广泛关注。针对综合能源系统的能量管理,文献[4]研究了含光伏、风机、储能及热电联供机组等单元的微网运行优化问题,将模型转化为混合整数线性规划问题求解;文献[5]利用改进的遗传算法,进行工业园区综合能源系统的能量管理方法研究;文献[6]研究了含可再生能源发电的电热综合能源系统的优化调度问题,利用改进的粒子群优化算法求解能量调度方案。上述研究在综合能源系统的能量管理和优化调度方面取得了一定的成果,但这些工作均是在对可再生能源出力和负荷需求进行预测的基础上进行的,求解效果依赖于预测的准确性。然而,受天气变化的影响,可再生能源发电是高度间歇性和随机性的。这些不确定性的资源与亦具有不确定性的用户负荷相结合,导致系统中供需双侧随机变化,为系统的能量优化管理带来巨大挑战。
为了应对综合能源系统中的不确定性,文献[7-8]采用随机规划方法对不确定性进行建模,分析不确定性因素的概率分布。然而,传统随机规划方法中误差场景的数目直接影响能量管理模型的求解效果。若场景数目过少,则难以真实反映可再生能源的不确定性;而场景数目过多,则求解难度及求解时间会大幅增加。此外,文献[9-10]采用鲁棒优化技术将不确定性因素采用不确定性集进行刻画,求取在最坏情况下的最优运行方案。然而,鲁棒优化算法采用不确定性集对不确定性因素进行刻画,往往难以选取合适的不确定性集[11]。
为了克服上述方法的缺点,本文引入无模型的强化学习(reinforcement learning, RL)方法以应对电热综合能源系统能量管理问题中可再生能源(源)和异质负荷需求(荷)的不确定性问题。基于马尔可夫决策过程(Markov decision process, MDP)理论的强化学习是一种重要的机器学习方法,具有强大的自主学习能力和适应能力[12]。强化学习中的智能体通过和环境进行交互,通过“试错”的方式不断自适应地学习探寻到最优策略[13]。强化学习不需要系统不确定因素的分布知识,是解决含不确定性因素的优化问题的很有潜力的方法,已被作为潜力解决方案引入智能电网、建筑等的运行优化和能量管理中[14-15]。
在采用强化学习进行综合能源系统的能量管理方面,已有学者进行了初步探索。文献[16]将综合能源微网的调度问题建模为马尔可夫决策过程,采用纳什(Nash)博弈和Q-learning算法实现能量管理及多主体运行策略的制定。文献[17]为应对系统中光伏出力和异类负荷的随机不确定性,提出了一种基于Q-learning的冷热电联供微网能量调度方法。文献[18]提出了一种基于强化学习的智慧能源枢纽运行优化方法,所提方法不需要系统动力学的任何知识,能够同时降低电费和天然气费用。然而,传统的强化学习是表格型的方法,仅适用于离散状态空间或小状态空间问题。如果直接采用强化学习处理综合能源系统的能量管理问题,需要将系统的状态量进行离散,离散化得到的状态数量随着自由度的增加会呈指数倍增长,从而出现维数灾难问题[19]。为应对该问题,本文将深度强化学习引入所研究的问题中,提出一种基于深度Q学习网络(deep Q-learning network,DQN)的电热综合能源系统能量管理方法。深度Q学习网络采用深度学习对Q-learning进行函数近似,避免对状态空间的离散化操作。此外,不同于传统方法,本文所提方法不需要可再生能源出力以及电热负荷需求的预测信息,能够自适应地对源和荷的随机波动做出响应。
文章首先对强化学习方法进行详细介绍,然后确定电热综合能源系统的能量优化管理问题的目标和约束,并将该问题表述为马尔科夫决策过程,进而采用DQN求解电热综合能源系统的能量管理问题。
1 强化学习方法
1.1 马尔科夫决策过程
强化学习的经典研究是基于马尔科夫决策过程[19],即系统下一时刻状态仅与当前时刻状态和动作有关。其问题模型通常被表示为一个元组
智能体在当前状态s采取动作a∈A(s),收到环境反馈的奖励r(s,a),并且以T(s,a,s′)的概率转移到下一状态s′∈S,其中A(s)表示在状态s可采取动作的集合。此过程可无限进行下去,也可以到终止状态处结束。策略π为状态到动作的映射:S×A→[0,1]。智能体的目标是通过调整策略来最大化累积奖励。通常可以使用状态-动作值函数Qπ(s,a)来衡量某个策略π的优劣程度。给定一个策略π,状态-动作值函数定义如下:
(1)
式中:Eπ[·]是策略π下的期望;s0是初始状态;a0是初始动作;t是时间槽的索引;rt是时间槽t时的奖励;γ∈[0,1]为折扣因子,表示未来奖励在累积奖励中所占的影响比重,γ越大表示越重视对未来的奖励。
1.2 Q学习算法
Q学习算法是解决马尔科夫决策过程的经典方法,是一种不基于环境模型的强化学习算法。在Q学习算法中,内部维护一个状态-动作值函数表Q(st,at),采用Q(st,at)值代表在状态st执行动作后获得的累积折扣奖励。智能体通过与环境反复地交互,利用获得的反馈信息不断地训练更新值函数,最终学习到完成目标的最优策略。Q函数的迭代更新公式表示如下:
Qt+1(st,at)=Qt(st,at)+αδt
(2)
式中:α为学习率;δt表示时间差分误差,表示为:
δt=rt+1+γQt(st+1,a′)-Qt(st,at)
(3)
式中:a′是状态st+1时能够执行的动作。
1.3 DQN算法
经典强化学习是表格型的方法,在处理高维状态空间或连续状态空间的问题时,存在维数灾难的问题。受深度学习[20]强大表征能力的启发,研究人员将深度学习和强化学习相结合,得到了深度强化学习。深度强化学习采用深度学习对强化学习进行函数近似,利用深度神经网络强大的函数逼近能力,使智能体不需要遍历每个状态或状态-动作对就可以对值函数进行表征,因此避免了维数灾难问题。深度强化学习使强化学习能够扩展到一些以前难以处理的问题,比如高维状态空间下的决策问题[21]。
DeepMind公司在Q学习算法和深度学习的基础上,提出了深度Q学习网络(DQN)[22]。DQN使用了经验回放机制和目标网络技术,其训练过程如图1所示。

图1 DQN训练过程示意图Fig.1 The training process of DQN
经验回放机制:强化学习中的样本是有关联的,训练结果难以收敛。经验回放机制通过存储智能体的经验et=(st,at,rt,st+1)形成记忆序列。训练时,每次从经验回放池中随机提取小批量的经验,然后根据随机梯度下降法更新网络参数。
目标网络:为了使DQN算法的性能更稳定,建立2个结构一样的神经网络,即一直在更新神经网络参数的Q网络和用于更新Q值的目标Q网络。DQN使用参数为θ的深度神经网络(Q网络)来逼近动作值函数,表示为Q(s,a;θ) ≈Qπ(s,a)。训练过程中,通过最小化损失函数进行参数更新:
Lt(θt)=E(s,a,r,s′)[(y-Q(s,a;θt))2]
(4)
式中:Lt(·)为t时的损失函数;θt为t时Q网络的参数;E(·)表示数学期望;y为Q网络的优化目标值,表示为:
(5)
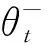
E(s,a,r,s′)[(y-Q(s,a;θt))θtQ(s,a;θt)]
(6)
2 电热综合能源系统的能量优化管理问题
2.1 电热综合能源系统
电热综合能源系统通常由能量转化单元、能量存储单元、能量传输网络和用户负荷组成,同时能够与上级主电网和天然气供应商进行能量交互。为进行具体分析,本文以如图2所示的电热综合能源系统为例进行研究,系统中的能量转化单元包括热电联供机组(combined heat and power, CHP)、燃气锅炉(gas boiler, GB)、电锅炉(electric boiler, EB)、可再生能源发电(renewable generation, RG)单元光伏,能量存储单元为蓄电池(battery, BA),用户负荷包括电负荷和热负荷。
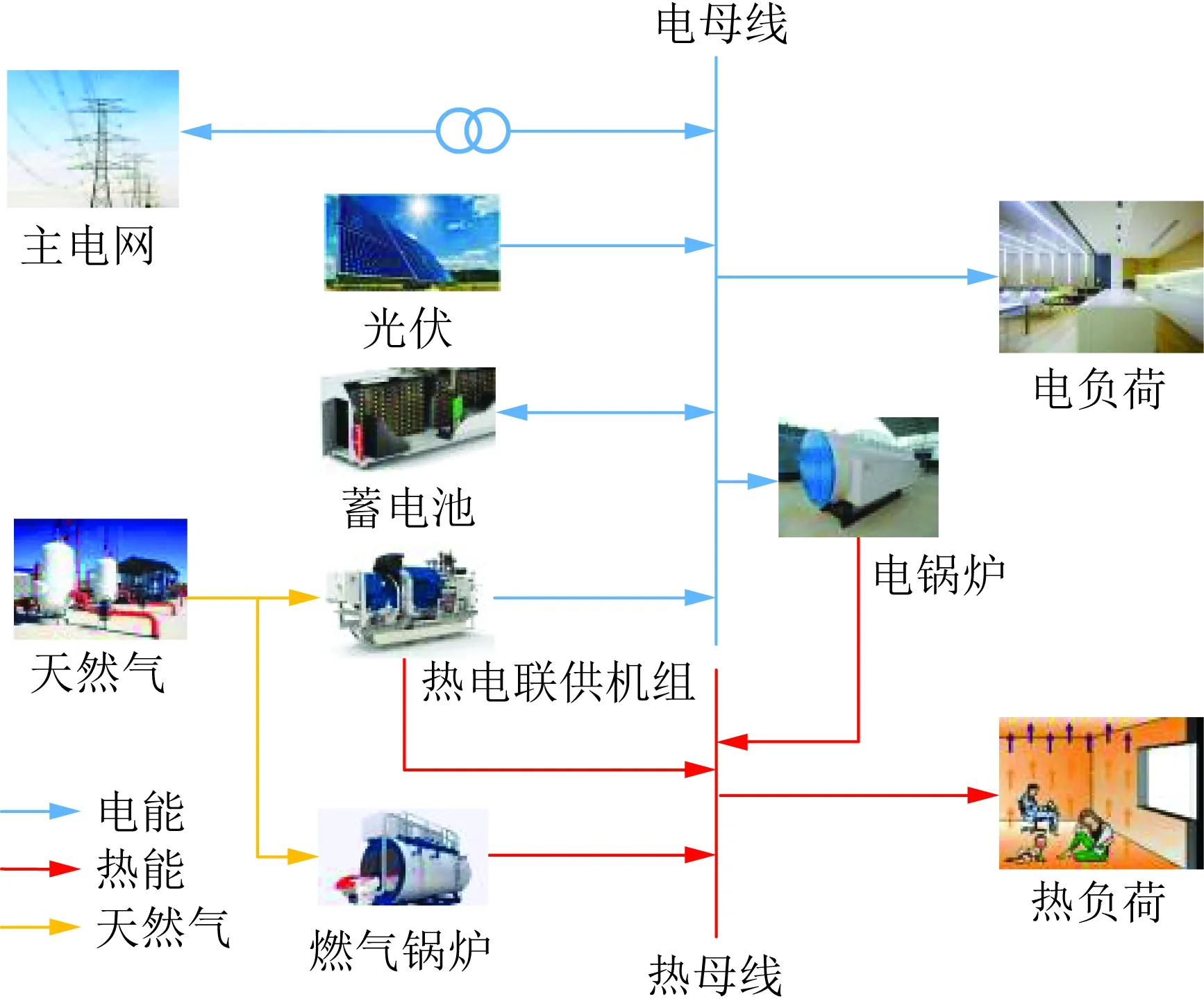
图2 电热综合能源系统示意图Fig.2 Schematic diagram of the integrated electricity-heat energy system
电热综合能源系统各个元件特性详述如下:
1)热电联供机组。
热电联供机组是实现综合能源系统热、电联供的重要设备,其消耗天然气提供电能和热能。热电联供机组在时间槽t时输出的电功率计算如下:
PCHP(t)=vCHP(t)HNGηCHP
(7)
式中:PCHP(t)为时间槽t时热电联供机组输出的电功率;vCHP(t)为热电联供机组消耗的天然气量;HNG为天然气热值;ηCHP为热电联供机组的电效率。
热电联供机组输出热功率与电功率的比值为热电比b,可表示为:
(8)
式中:HCHP(t)时间槽t时热电联供机组输出的热功率。
2)燃气锅炉。
燃气锅炉消耗天然气提供热能,燃气锅炉在时间槽t时输出的热功率计算如下:
HGB(t)=vGB(t)HNGηGB
(9)
式中:HGB(t)为燃气锅炉输出的热功率;vGB(t)为燃气锅炉消耗的天然气量;ηGB为燃气锅炉的效率。
3)电锅炉。
电锅炉消耗电能产生热能,电锅炉在时间槽t时输出的热功率计算如下:
HEB(t)=PEB(t)ηEB
(10)
式中:HEB(t)为电锅炉输出的热功率;PEB(t)为电锅炉的输入电功率;ηEB为电锅炉的效率。
4)蓄电池。
蓄电池在时间槽t的荷电状态(state of charge, SOC)为:
SSOC(t)=SSOC(t-1)-ηBA·PBA(t)·Δt/QBA
(11)
式中:PBA(t)是蓄电池的运行功率,为正时表示其处于放电状态,为负时表示其处于充电状态;QBA是蓄电池的容量;Δt是相邻两个时间槽的时隙长度;ηBA是蓄电池的充/放电系数,表示为:
(12)
式中:ηch∈(0, 1]为蓄电池的充电效率;ηdis∈(0, 1]为蓄电池的放电效率。
2.2 系统能量优化管理问题的数学描述
2.2.1目标函数
综合能源系统能量管理问题的目标是协调系统中各单元出力,获得最小化系统运行成本。系统运行成本主要由与主网能量交互成本、消耗的天然气成本、蓄电池的折旧成本构成。系统总成本表示为:
minC=min(CMG+CNG+CBA)
(13)
式中:C为系统总成本;CMG为与主网能量交互成本;CNG为消耗的天然气成本;CBA为蓄电池的充放电折旧成本[23]。各项成本具体表示如下:
(14)
(15)
(16)
式中:PMG(t)为时间槽t时综合能源系统与主网的电力交换功率,为正时表示向主网购电,为负时表示系统向主网售电;εMG(t)为时间槽t时的电价,PMG(t)为正时电价为购电电价,PMG(t)为负时电价为售电电价;εNG(t)为时间槽t时的天然气单价;ρBA是蓄电池的折旧成本系数;T为对系统进行能量管理所考虑的总时间槽个数。
2.2.2约束条件
综合能源系统能量管理问题的约束条件包括电功率平衡约束、热功率平衡约束、外部能源供应约束和元件运行上下限约束。
1)电功率平衡约束。
式(17)为时间槽t时系统电功率平衡约束的数学表述。等式左侧包含系统与主电网的电力交互功率、可再生能源发电单元的输出功率、蓄电池的充/放电功率及热电联供单元的输出电功率,等式右侧包括电锅炉的耗电功率及用户的电负荷。
PMG(t)+PRG(t)+PBA(t)+PCHP(t)=
PEB(t)+Pload(t)
(17)
式中:PRG(t)为可再生能源发电单元RG的输出功率;Pload(t)为时间槽t时的用户电负荷。
2)热功率平衡约束。
式(18)为时间槽t时系统热功率平衡约束的数学表述。等式左侧包含热电联供单元的输出热功率、燃气锅炉的输出热功率及电锅炉的输出热功率,等式右侧为用户的热负荷。
HCHP(t)+HGB(t)+HEB(t)=Hload(t)
(18)
式中:Hload(t)为时间槽t时的用户热负荷
3)外部能源供应约束。
综合能源系统与主网间的功率交互有上下限约束:
(19)
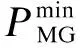
对于天然气供应,需满足以下约束:
(20)
vNG(t)=vCHP(t)+vGB(t)
(21)

4)元件运行上下限约束。
综合能源系统中各元件均需满足相应的运行范围约束,对于热电联供单元的输出电功率、燃气锅炉及电锅炉的输出热功率和蓄电池的充/放电功率,分别要满足如下运行上下限约束:
(22)
(23)
(24)
(25)
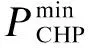
对于蓄电池,为了避免深度充放电对蓄电池造成损害,蓄电池的荷电状态被限定在一定范围内:
(26)
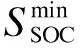
3 基于深度强化学习的系统能量优化管理
3.1 能量管理问题的马尔科夫决策过程描述
电热综合能源系统能量优化管理的目标是最优地管理系统中各元件在每个时间槽的出力,从而降低系统总运行成本。由于综合能源系统中间歇性可再生能源出力和电负荷、热负荷需求是随机的,综合能源系统的能量管理问题可以看作是不确定条件下的序贯决策问题。在本节中,将电热综合能源系统的能量管理问题表述为马尔科夫决策过程,定义状态、动作、状态转移函数和奖励函数。
1)状态空间描述。
在时间槽t,智能体接收到环境的观测状态,即综合能源系统的状态st。系统状态包括用户负荷(电负荷和热负荷)、可再生能源发电功率、蓄电池的荷电状态,以及所处的运行时间槽t。因此,状态st表示如下:
st=[Pload(t),Hload(t),PRG(t),SSOC(t),t]
(27)
2)动作空间描述。
电热综合能源系统能量管理的目标是最优地确定热电联供单元的输出电功率和输出热功率、蓄电池的充/放电功率、综合能源系统和主网的交互功率、GB的输出热功率、EB的输入电功率和输出热功率。由于PCHP确定后,HCHP可由式(8)计算得到;HGB确定后,HEB可根据式(18)确定;进而PEB、PMG也可分别通过式(10)、(17)计算确定。也就是说,在PCHP、PBA、HGB确定后,其他量可以迅速得到。将PCHP、PBA、HGB按各自范围分别划分为K1、K2、K3个离散的动作选择,分别均匀离散化为动作空间ACHP、ABA和AGB:
(28)
(29)
(30)
故电热综合能源系统的动作可以表示为:
(31)
这里,a∈A,k1∈[1,K1],k2∈[1,K2],k3∈[1,K3]。
3)状态转移函数建立。
环境状态st转移到状态st+1表示为:
st+1=f(st,at,ωt)
(32)
式中:ωt表示随机量。式(32)表示状态转移不仅受动作at的控制,而且还受随机性的影响。对于Pload、Hload和PRG,由于下一时刻的用能需求和可再生能源出力未知,状态转移受随机性影响。由于很难为随机性建立一个精确的模型,本文并未对其进行建模,而是利用神经网络学习状态转移。
4)奖励函数构建。
在IES状态st时,智能体执行动作at后获得奖励rt。电热综合能源系统能量优化管理的目的是最小化系统运行成本,因此,在时间槽t,智能体获得的奖励可表示为:
rt(st,at)=-[CMG(st,at)+CNG(st,at)+
CBA(st,at)]×0.001
(33)
其中,乘以0.001是对成本值进行缩小。
电热综合能源系统能量管理动作a的优劣程度可以使用状态-动作值函数Qπ(s,a)来评估,其目标是找到最优策略π*以最大化状态-动作值函数。
(34)
3.2 基于DQN的系统能量管理方法
由于电热综合能源系统中未来的可再生能源出力和用户负荷需求是未知的,因此很难解析地确定最优能量管理策略π*。强化学习不需要随机过程的统计模型,是一种无模型的学习方法,因此非常适用于本文的含不确定性因素的电热综合能源系统能量优化管理问题。
然而,由于本文中的电热综合能源系统能量管理问题的状态空间(如式(27)中所示的电负荷、热负荷、可再生能源发电等)是连续的,需要极其大的表来近似Q函数,并且更新如此大的表也是非常有挑战性的,故传统的强化学习方法已无法适用。因此,本文采用DQN算法进行电热综合能源系统的能量优化管理。基于DQN的综合能源系统能量管理方法流程如图3所示。
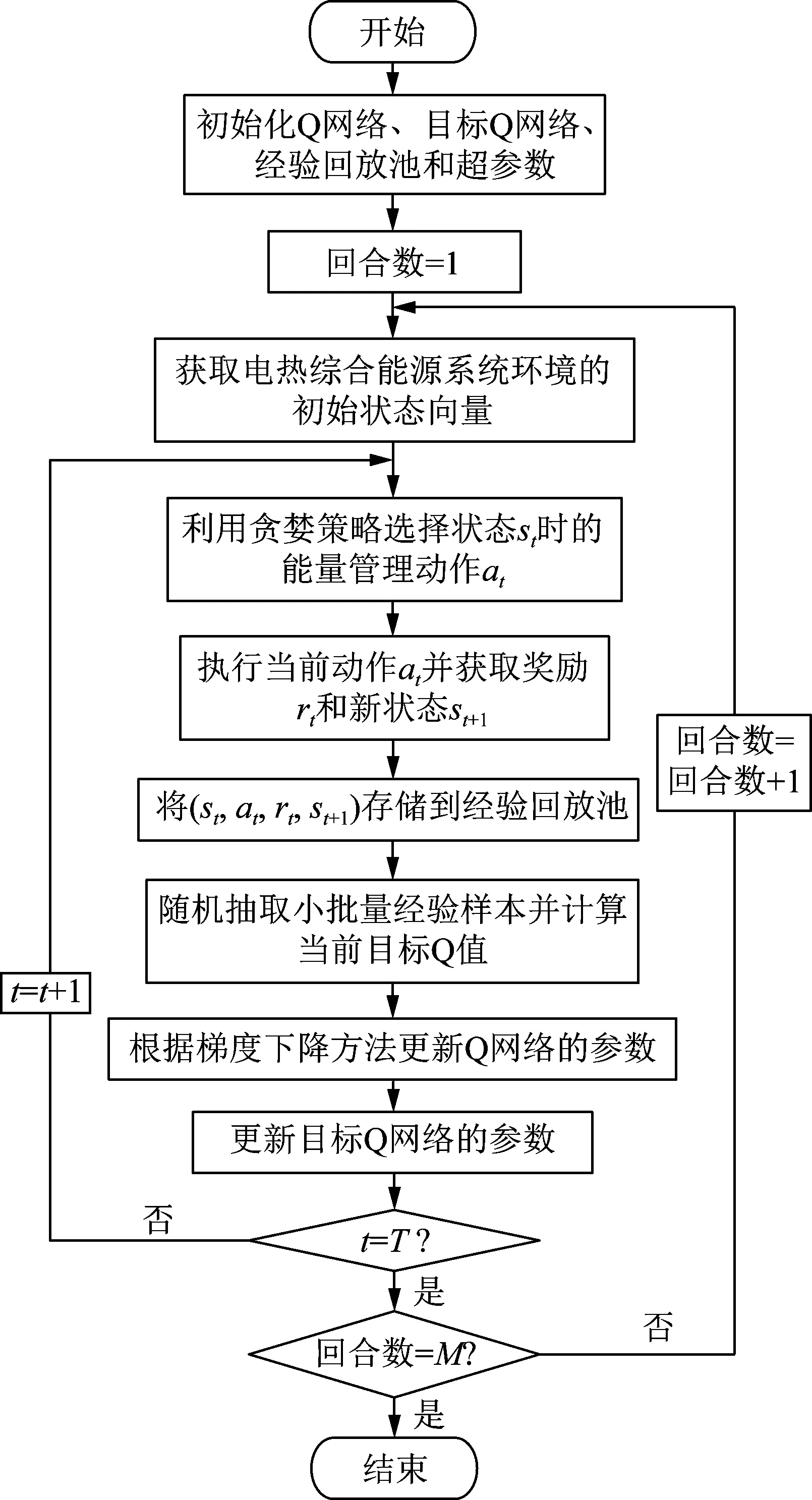
图3 基于DQN的综合能源系统能量管理流程图Fig.3 Flowchart of the DQN-based IES energy management method
4 算例分析
4.1 仿真算例设置
本节对所提方法进行仿真分析,以验证所提出的基于DQN的综合能源系统能量管理策略的有效性。以图2所示的电热综合能源系统作为算例,其中,可再生能源发电装置为太阳能光伏装置。电负荷、热负荷和光伏数据基于开源的CREST模型[24]产生。该模型已经过定性验证,且在很多研究中广泛应用[25-26]。该模型产生的数据包含随机性,模拟了真实电热综合能源系统环境中源和荷的不确定性。由CREST模型生成了12月至次年3月的数据,每月前23天的数据用于训练,每月的剩余天数用于性能评估。系统能量管理时段长度设置为1天,Δt为15 min。
电热综合能源系统中元件的运行参数如表1所示。与主网交换电功率的范围为[-3 , 3] MW,与天然气供应商交换功率的范围为[0 , 4] MW,蓄电池的容量是1 000 kW·h,综合能源系统其他参数见表2。电价采用分时电价,购电价格方面,谷电价为0.17元/(kW·h) (23:00—07:00),峰电价为0.83元/(kW·h) (12:00—19:00),其他时刻为平电价0.49元/ (kW·h);售电价格为购电价格的0.4倍。天然气的单价为3.45元/m3,天然气热值为9.88 kW/m3。
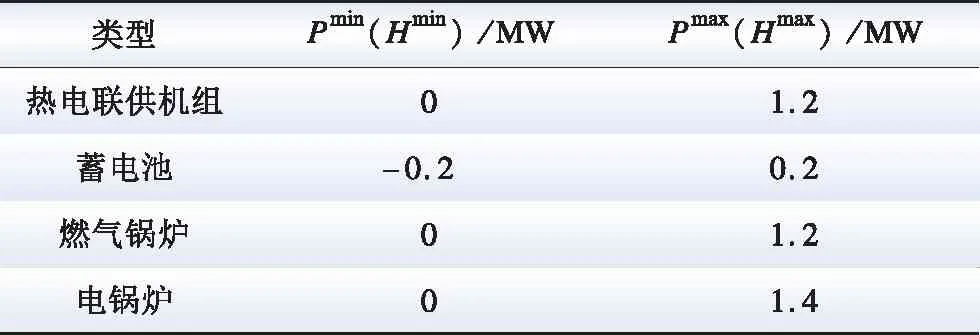
表1 综合能源系统中元件的运行参数Table 1 Operational parameters of the IES
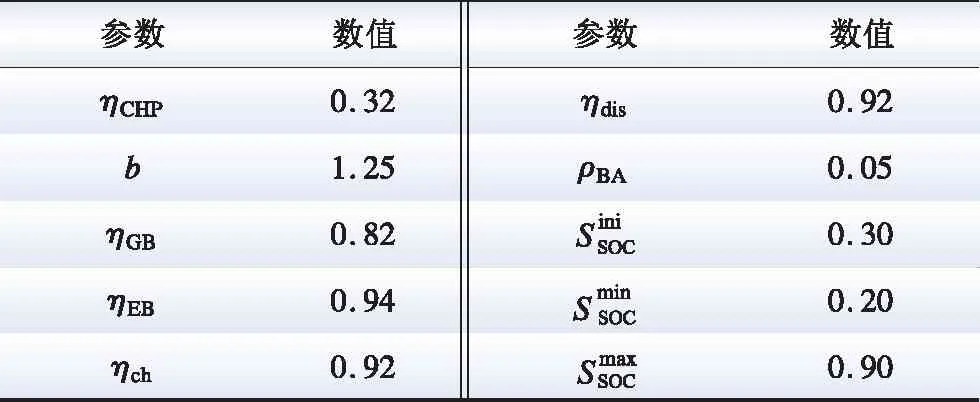
表2 综合能源系统的其他参数Table 2 Other parameters of the IES
所提深度强化学习方法是使用TensorFlow平台实现的。DQN网络的输入为5维状态向量st,输出为状态-动作对的Q值,本文将PCHP(t)、PBA(t)、HGB(t)分别以0.2 、0.1 、0.2 MW为间隔进行离散,即CHP的可选动作为{0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2}MW,蓄电池BA的可选动作为{-0.2, -0.1, 0, 0.1, 0.2}MW, 燃气锅炉GB的可选动作为{0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2}MW。超参数,如深度神经网络隐含层的层数和每个隐含层的神经元数目,根据深度学习社区[27]推荐的常用做法选取,并根据训练数据进行试错调整。折扣因子为0.99,学习率为0.001,mini-batch大小为128,经验池大小为10 000,隐含层层数为2层,每层分别有128、256个神经元,激活函数为线性修正函数 (rectified linear units, ReLU)。
4.2 能量管理结果分析
在将所建深度Q学习网络应用于系统能量管理之前,首先训练DQN的参数。智能体接收电负荷、热负荷及光伏出力的观测数据,然后根据3.2节中的训练过程调整DQN网络的参数,即权重θ。在利用训练数据对DQN网络进行离线训练后,得到的网络被保存以用于系统的能量优化管理。离线训练完成的标志是随着迭代次数的增加,奖励值变化幅度较小,不再呈明显增加趋势,即网络达到收敛。应用训练好的DQN对系统进行能量管理,输入数据是当前电负荷、热负荷、光伏发电量、蓄电池SOC及时间槽,输出是CHP的电功率、蓄电池的充/放电功率和燃气锅炉的热功率。
为了说明所提方法的能量管理结果,选取测试集中的数据进行测试,首先以一个冬季典型日(1月25日)为例进行说明,结果如图4和图5所示。图4为电能管理结果,包括和主网的电功率交换、光伏发电、热电联供机组输出电功率、蓄电池运行功率和电锅炉的输入电功率,分别表示为GRID、PV、CHP-E、BA和EB-E;电锅炉消耗电功率,因此其电能管理结果用负值表示。图5为热能管理结果,包括燃气锅炉、电锅炉、热电联供机组输出的热功率,分别表示为GB、EB-H和CHP-H。

图4 基于DQN的电能管理结果Fig.4 Electric power management results based on DQN method
由图4可以看出,系统向主电网购电情况基本跟随电价变化。在谷电价和平电价阶段,向主网购电以满足用户电负荷需求。在峰电价阶段,电负荷主要由热电联供单元满足。在电负荷较小而热负荷较大时,热电联供单元多生产的电能售回电网,如13:00—14:00时段等。蓄电池在谷电价时充电,并在峰电价时放电以减少系统运行成本,如12:15—12:30时段和13:45等。

图5 基于DQN的热能管理结果Fig.5 Heat power management results based on DQN method
由图5可以看出,系统中的热能供应来自于CHP、GB和EB。EB为谷电价时热能的主要来源,谷电价阶段且热负荷高于1.4 MW时,EB所制热不能满足热负荷需求,GB制热进行补充,如05:45—06:45时段。在平电价阶段,热负荷主要由GB提供,当热负荷高于1.2 MW时,GB的出力不能满热负荷需求,通过增加EB或EB与CHP的出力进行补充。在峰电价时,热负荷主要由CHP和GB提供,当两者出力之和不能满足热负荷需求时,通过增加EB的出力进行补充。这表明本文提出的基于DQN的能量管理方法能够不断优化各设备出力以降低系统运行成本。
4.3 对比结果分析
为了验证所提方法的有效性,将本文提出的基于DQN的综合能源系统能量管理方法与基于Q学习的能量管理方法以及依赖预测信息的调度方法进行比较。其中,Q学习方法的动作空间划分与DQN方法的一致。对于依赖预测信息的调度方法(传统方法),采用神经网络对光伏出力和电、热负荷进行预测,然后类似文献[4],采用优化软件进行求解。对采用3种方案在测试集数据运行得到的日运行成本进行比较,统计结果如表3所示。图6给出了从测试集中随机选取的10个测试日的日运行成本结果。

表3 不同能量管理方法的日运行成本统计结果Table 3 Statistics of the daily operation costs under different methods元
由表3可以看出,基于DQN的能量管理方法的平均日运行成本为17 621元;基于Q学习方法的平均日运行成本为18 516元,较DQN方法增加了5.08%;基于预测信息的调度方法的平均日运行成本为18 133元,较DQN方法增加了2.91%。从日运行成本的最大值、最小值、平均值以及随机选取的测试日的日运行成本来看,DQN能量管理方法较其他2种能量管理方法获得了更好的经济性能,能有效地降低系统运行成本。
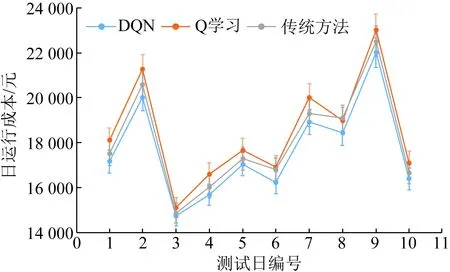
图6 不同方法的系统运行成本对比Fig.6 Comparison of system operation costs under different methods
5 结 论
本文提出了一种用于综合能源系统运行优化的能量管理方法。将电热综合能源系统的能量管理问题表述为一个马尔科夫决策过程,其中考虑了可再生能源发电和负荷需求的不确定性。为求解该马尔科夫决策过程,提出了一种基于DQN的电热综合能源系统能量管理方法。所提方法不依赖于综合能源系统中不确定因素的预测信息及分布知识,可以根据系统的观测状态直接确定系统的能量管理策略,因此避免了由于预测或建模不准确而导致的后续能量管理策略的不可靠和大偏差。将所提方法在测试集上进行测试,结果表明所提方法能够不断优化各设备出力以降低系统运行成本。将该方法与基于传统Q学习的能量管理方法进行对比,对运行得到的日运行成本的平均值、最大值和最小值进行比较,验证了所提方法的有效性,表明了本文所提出的基于DQN的综合能源系统能量管理方案能够更好地实现系统的能量管理与运行优化。
