光伏并网与有源滤波的统一控制策略研究

伍思孟，郝正航，雷廷浩，陈卓

光伏并网与有源滤波的统一控制策略研究

伍思孟，郝正航，雷廷浩，陈卓

（贵州大学 电气工程学院，贵州 贵阳 550025）

将光伏并网与有源滤波相结合的统一控制策略可解决光伏发电系统在光照不足时设备利用率低、有源滤波器功能单一、成本高等问题。但传统的最大功率跟踪控制扰动观测法通过施加扰动量寻找最大功率点，会使光伏模块的输出电流持续振荡，严重影响谐波补偿电流从检测到输出的精度。与传统方法不同，在光伏并网与有源滤波相结合的控制策略中改进分段式变步长电导增量法，消除光伏电池输出电流振荡，并加强特定奇次谐波补偿，改进系统工作模式及判据，进而提高电能质量。通过MATLAB/SIMULINK对所提控制策略在环境和负载持续切换的条件下进行对比仿真验证，仿真结果体现了该改进控制策略的有效性。

光伏并网；有源滤波；统一控制策略；分段式变步长INC算法；特定奇次谐波补偿

0 引言

传统的燃料能源是人类生存和发展的重要物质基础，随着能源危机和大气污染的日益严重，太阳能以其最丰富和最洁净的特点成为当今国内外最具发展前景的新能源之一[1]。由于天气阴晴和昼夜交替的原因，光伏发电存在间歇性、非线性、逆变器容量利用效率不高的问题[2]。光伏逆变器中的大量电力电子元器件，在逆变过程中不可避免会产生谐波，并对电网会造成谐波污染[3]。随着分布式光伏发电在电网中应用率的提高，如何利用逆变器剩余容量治理电能质量问题已成为目前国内外研究的热点[3-4]。

基于瞬时无功功率理论的有源滤波器（APF）可补偿谐波电流和无功功率，其电压型全桥结构与三相光伏并网发电系统中的并网逆变器主电路完全一致[5]。文献[6-11]提出了基于光伏并网和有源滤波的统一控制策略，将电能输送和电能质量治理集于一体，有效降低光伏并网的谐波含量并提高功率因数，但均未在并网指令电流的合成中考虑到逆变器的容量问题，且只进行光照或负载的单一变量单次变化实验，未对比验证系统在持续的环境和负载变化中的统一控制效果。文献[12]考虑谐波抑制和无功补偿的顺序和大小，确定并网指令电流合成方案具有一定的参考价值，但其设计的16种不同谐波和无功补偿情况十分复杂。文献[13]采用电导增量法（INC）稳定光伏电池最大功率，但其L型电路系统网侧电流谐波含量≥5%，超出国家标准，未研究光伏电池输出电流的振荡，在并网指令电流合成环节影响谐波补偿精度，对系统谐波治理产生影响。

为解决上述问题，本文基于光伏并网、谐波抑制与无功补偿三重功能相结合的统一控制策略，改进分段式变步长电导增量法，重点消除光伏电池输出电流振荡对谐波补偿电流的影响。本文还优化逆变器容量的判定依据，依据光照条件和非线性负载变化，设计合理的工作模式，使系统同时实现响应速度和谐波治理效果的提高，并采用MATLAB/SIMULINK仿真进行对比验证。

1 光伏并网与有源滤波的统一控制策略

1.1 控制原理

结合有源滤波功能的光伏并网系统结构主要由光伏电池PV、DC-DC升压斩波电路、三相全桥逆变器和传统的扰动观察法（P&O）最大功率跟踪模块、谐波和无功电流检测模块、指令电流合成及工作模式判定模块组成，如图1所示。

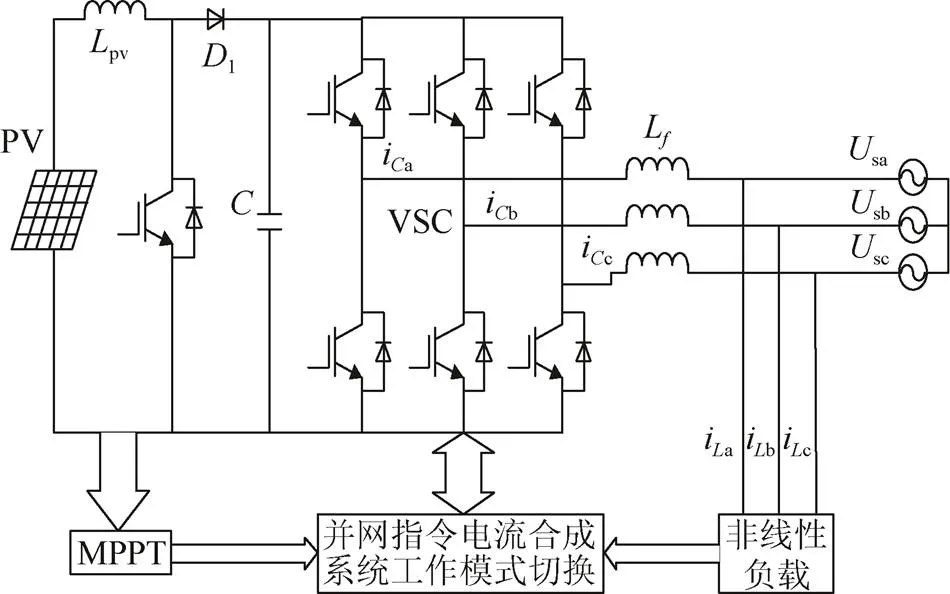
图1 系统结构

白天光照充足，光伏电池以最大功率发电的同时，系统根据容量限制谐波补偿；在阴天等光照不足时，加强谐波抑制并进行无功补偿。夜晚系统工作在仅APF模式，以提高设备的利用率[14-15]。

1.2 存在的问题

如图2所示，P&O算法通过扰动输出电压后观察光伏电池功率的变化，用两点功率差(k)–(k–1)近似代替微分d[16]。这种方法追踪速度快，但在系统最大功率点附近始终存在功率扰动、能量损失问题[17]。系统网侧电流通常存在白天谐波含量较高，超出5%，还需设置LCL电路再次滤波；但系统网侧电流夜间谐波含量却极低，说明问题并非源于谐波电流检测算法，应是白天传统P&O算法控制光伏电池，以定步长在最大功率点附近来回扰动而使输出电流持续振荡，导致系统补偿电流工作偏离原检测精度，网侧谐波含量昼夜偏差较大，应考虑更换MPPT算法。

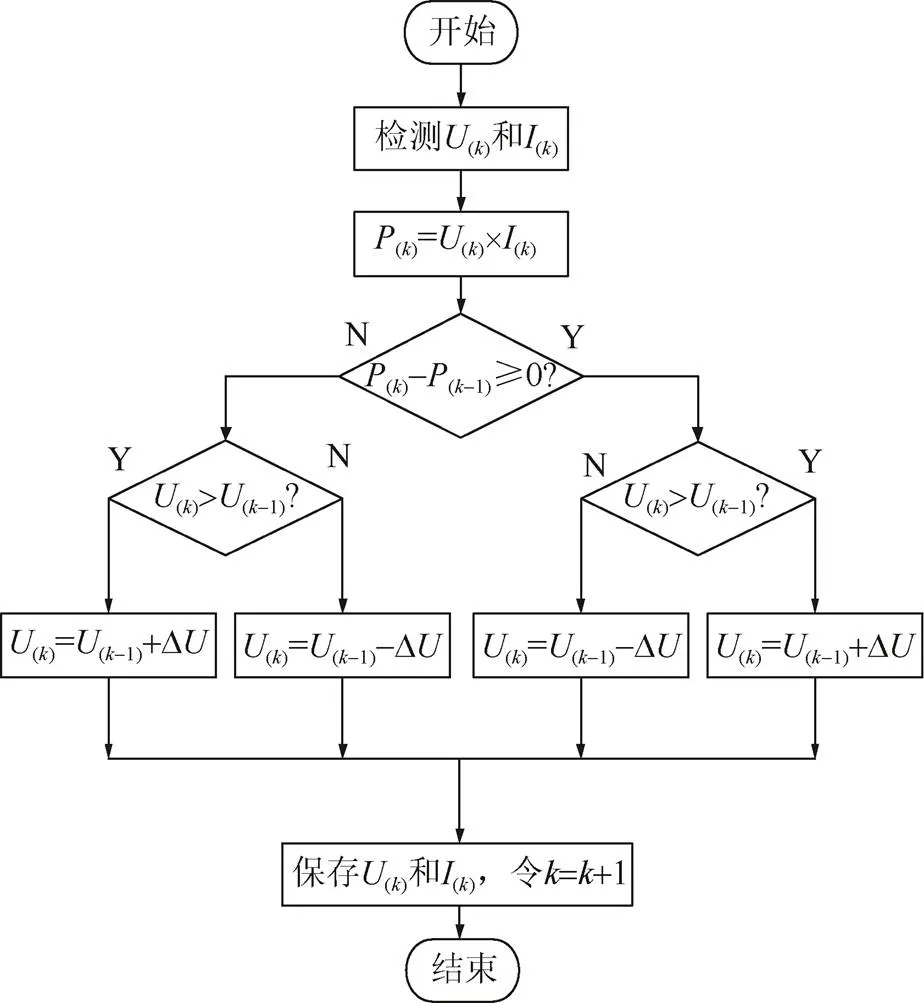
图2 传统的P&O流程图

传统的控制实验中光照条件改变仅在光伏电池输出功率波形的升降上验证。实际上，电网侧提供给负载的电流幅值也应随光照的提高而略微减小，或随光照的降低而略微增加。因此，不仅过于复杂的传统工作模式及判定方案需整合改进，系统的并网指令电流合成环节亦有待优化。

2 改进的分段式变步长电导增量法MPPT

P&O算法使光伏电池输出电流不断振荡，在并网合成环节持续影响谐波补偿电流的正常工作。INC算法虽然可减小功率的扰动和电流的振荡，找到d/d=0的点，但其精度的要求越高，跟踪的速度就越慢。因而对系统的统一控制策略优化，并非直接将传统的P&O算法更换为INC算法，还应考虑d/d的变化特征，对步长选取进行改进。

根据图3所示，光伏电池-特性曲线，选取|d/d|与斜率阈值的大小关系，将光伏电池-特性曲线划分为I、II、III段分别进行分析。在远离最大功率点的I、III段，采用较大的定步长提高响应速度；在靠近最大功率点II段，采用较小的变步长保持稳态精度。

图3 光伏电池P-U特性变化分段曲线

第I段对应|d/d|>且d/d>0的情况，此时|d/d|变化较大，应采用定步长Δ向右前进。

第II段对应|d/d|<的情况，|d/d|变化较小。若功率在最大功率点左侧，则d/d>0，系统选取持续变化的|d/d|与步长系数1的乘积1为采样步长向右逼近；若功率在最大功率点右侧，则d/d<0，系统选取持续变化的|d/d|与步长系数2的乘积2为采样步长向左返回。

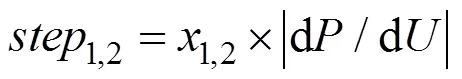
第III段对应|d/d|>且d/d<0的情况，此时|d/d|变化较大，应采用定步长Δ从右返回。

如图4所示，改进的分段式变步长INC算法流程以(k)–(k–1)=0和(k)–(k–1)=0临界条件，选取变步长3,4为步长系数3,4与变化的|d|的乘积。

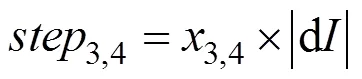
3 并网合成环节及工作模式的优化

3.1 并网指令电流的合成

并网合成环节的优化旨在无需占用逆变器更多容量的条件下，提升系统谐波治理效果。传统控制策略在光照充足使光伏电池输出功率过高时，逆变器容量或不足以全额补偿谐波；光照稍弱但系统重载谐波电流过高时，也可能存在有源滤波后网侧电流≥5%的问题。

如图5所示，通过改进基于瞬时无功功率原理的谐波电流检测法，针对干扰最大的5次、7次和11次谐波，加强特定奇次谐波的限幅补偿以降低系统谐波含量。

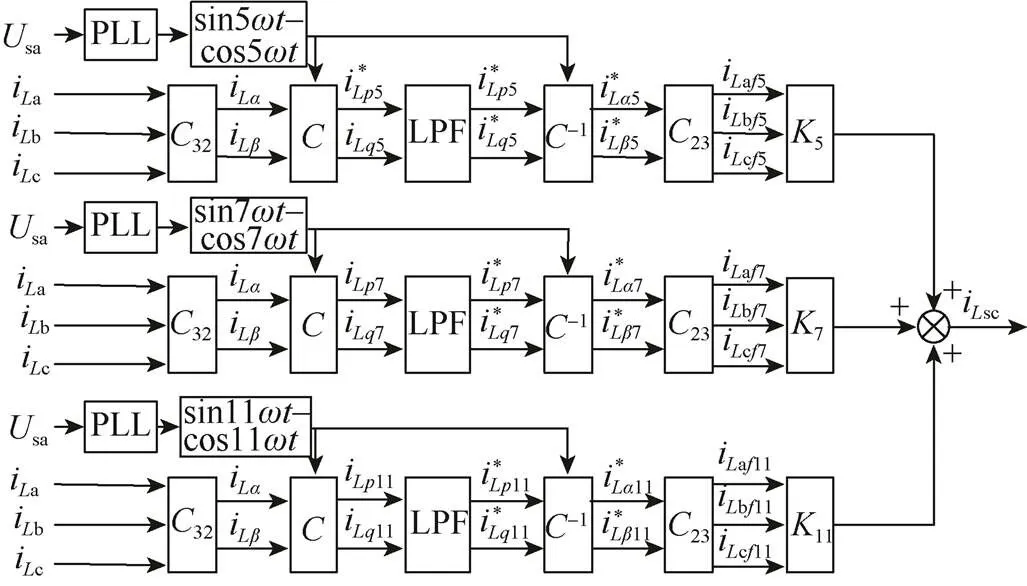
图5 基于ip–iq算法强化特定奇次谐波电流检测控制策略

将特定奇次谐波强化分量isc与谐波补偿信号ihc、无功补偿信号iqc叠加生成补偿电流hqs。

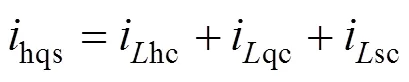
白天光伏有功基波信号pv与hqs在旋转坐标系

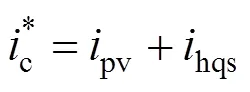
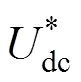
图6 直流侧电压控制结构

3.2 系统工作模式及判定

综合光照、温度等环境因素和网侧电流谐波含量、功率因数、逆变器容量等系统情况，设置系统运行于5种不同的工作模式：

（1）当光照强度较高且较低时，系统只进行光伏发电，无需进行谐波治理或无功补偿。

（2）当光照强度较高且较高时，系统优先输送有功能量，暂不考虑无功补偿。

（3）光照强度略低时，系统除光伏发电外，系统尽可能同时实现有源谐波和无功补偿的功能。

（4）光照略低且系统重载，模式3补偿后仍有≥5%，需单独对特定奇次谐波电流优化补偿。

（5）夜间系统运行在并联型APF模式。

本文改进比较条件，用光伏逆变器所允许的最大输出电流c_max代表逆变器容量，对前4种工作模式的判定流程如图7所示。

图7 容量分配及其判断流程图

4 仿真结果及分析

为对比验证该改进策略的有效性，根据图1采用MATLAB/SIMULINK搭建仿真模型，电网电压为380 V，系统频率为50 Hz，VSC容量为15 kVA，pv取4.6 mH，f取4 mH，直流侧电容为2 200 μF，直流侧电压设定800 V。光伏电池oc为468 V，m为400 V，sc为15.88 A，m为14.88 A，温度设定25 ℃，光照初始值1 000 W/m2，斜率阈值取3，步长系数1、2、3、4分别取0.5、0.1、0.002 9、0.000 1，仿真时长共3 s。

4.1 光伏电池MPPT控制

在优化后并网合成环节的统一控制策略中，分别采用改进后分段式变步长INC算法、传统P&O算法仿真对比，仅观察前1 s光照条件改变对光伏电池输出的影响。

光伏电池功率输出波形如图8所示，两种算法约在0.04 s追踪最大功率到5 952 W，此时传统P&O算法功率在最大功率点附近持续扰动且幅值相对较大约为350 W，而改进后INC算法功率扰动幅值非常小，约为3 W，其功率追踪的精度更高。0.5 s光照突然降低至600 W/m2，两种算法最大功率降低约3 570 W，此时传统P&O算法的扰动幅值立刻降低至2 W，而改进后INC算法最大功率扰动幅值也在瞬时微增后迅速稳定至1.5 W，其波动程度仍优于在前者。

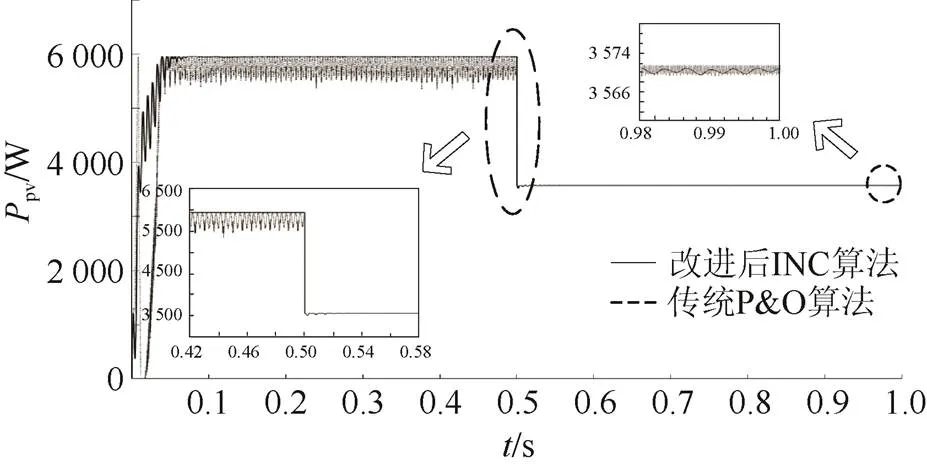
图8 改进后INC和传统P&O算法光伏电池输出功率波形对比

对比图9光伏电池电流输出波形，由于传统P&O算法始终在最大功率点附近以定步长来回扰动，导致光照降低前对应光伏电池输出电流约在13~15.6 A间保持上下振荡，而改进后INC算法能以变步长稳定追踪至d/d=0的点，电流幅值变化较小，约为14.82~14.92 A；光照降低后传统P&O算法光伏电池输出电流减小，但仍在8.9~9.04 A间振荡，而改进后INC算法的光伏电池输出电流振荡更小，仅为8.9~8.94 A，具有更好的稳态性能。

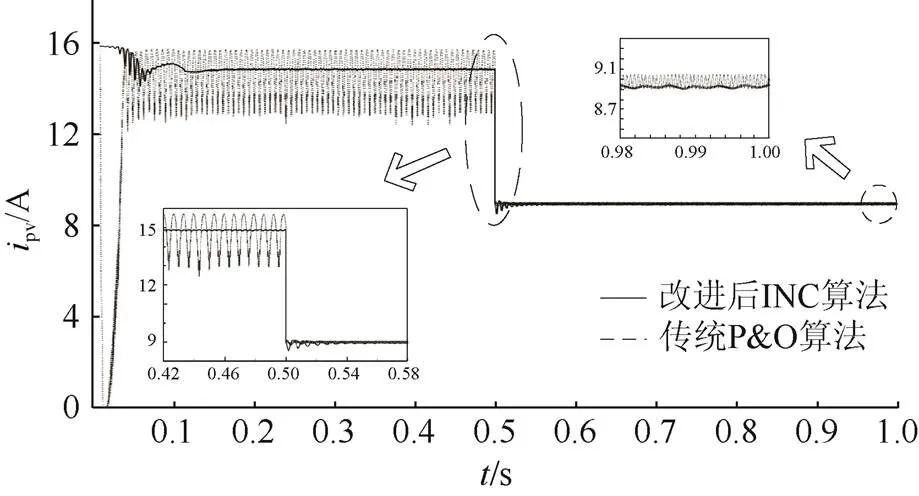
图9 改进后INC和传统P&O算法光伏电池输出电流波形对比

改进后INC算法拥有几乎相同的响应速度和更高的追踪精度，尤其是光伏电池输出电流扰动的消除，使并网指令电流中补偿电流稳定工作而不因光伏电流的振荡而偏离其检测的精度，间接提升处于模式2、3、4的系统谐波抑制效果。

4.2 系统统一控制

在1.5 s重新提高光照条件至1 000 W/m2，2.5 s再次降低为600 W/m2，1 s接入重载系统工作于模式3；非线性负载在2 s时刻继续加重系统切换至模式4，网侧电流可能超出国标要求。

图10（a）（b）（c）分别为0.5 s、1.5 s、2.5 s光照改变时网侧a相电流的波形。图10（a）（c）中电流幅值分别在0.5 s、2.5 s略微增大，表示光照降低光伏电池提供给负载的电流变小，电网提供的电流变大；图10（b）中电流波形幅值在1.5 s出现略微降低，表示光照提高光伏电池提供给负载的电流变大，电网提供的电流变小，网侧电流大小随光照变化立刻响应，显示并网合成环节的优化非常有效。

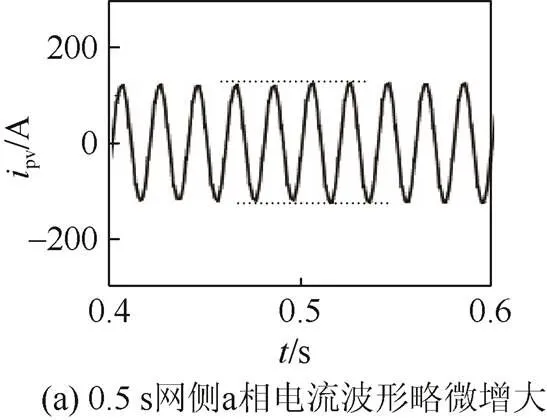
对图10（b）所示的1.5 s电流波形变化前后进行频谱分析，改进后INC算法控制的谐波含量分别如图11（a）（c）所示；对应时刻传统P&O算法1.5 s电流波形变化前后的频谱分析分别如图11（b）（d）所示。

光照提高前系统处于模式2，改进后INC算法网侧电流值为3.99%，而对应时刻传统P&O算法网侧电流值为4.56%；光照提高后系统处于模式3，如图12（a）并网指令电流中并无特定奇次谐波强化分量，改进后INC算法网侧电流值为4.45%，而对应时刻传统P&O算法网侧电流值为6.14%。在其他条件一致的情况下，改进后INC算法在一定程度上可解决传统的统一控制策略谐波电流补偿精度的偏移。

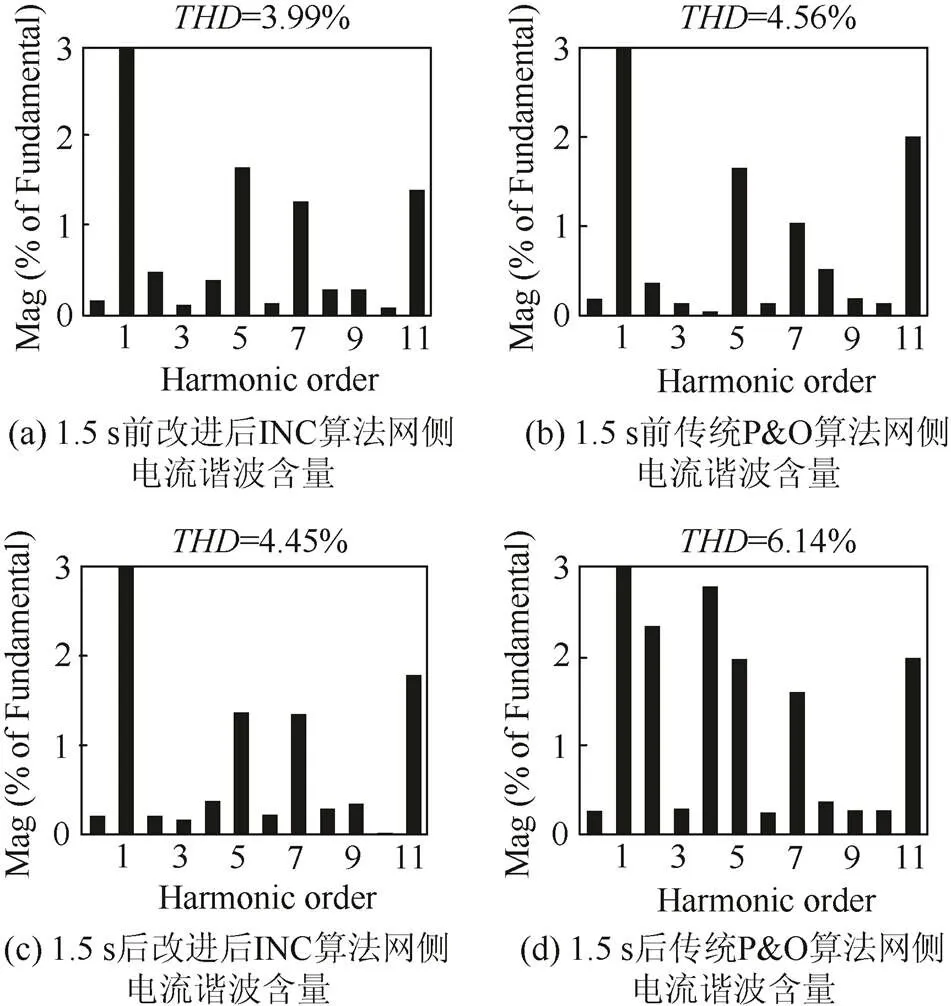
图11 改进后INC和传统P&O算法1.5 s前后网侧电流谐波含量对比

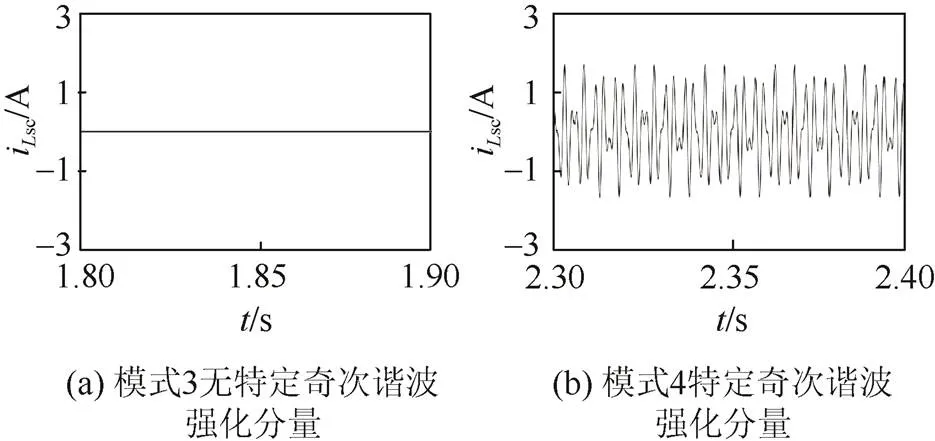
图12 模式3与模式4系统并网指令电流中iLsc波形对比

对图10（c）所示的2.5 s电流波形进行频谱分析，改进后INC算法控制的谐波含量分别如图13（a）（c）所示，对应时刻传统P&O算法1.5 s电流波形变化前后的频谱分析分别如图13（b）（d）所示。光照降低前系统处于模式4，如图12（b）所示。并网指令电流中加入特定奇次谐波强化分量，改进后INC算法网侧电流值为5.16%，而对应时刻传统P&O算法网侧电流值为7.16%；光照降低后系统退回模式3，并网指令电流中取消特定奇次谐波强化分量，改进后INC算法网侧电流值为4.77%，而对应时刻传统P&O算法网侧电流值为5.31%。在重载的情况下，网侧电流幅值更小，谐波对其影响更大，而改进后INC算法在强光照的条件下对系统谐波治理的效果提升更显著。

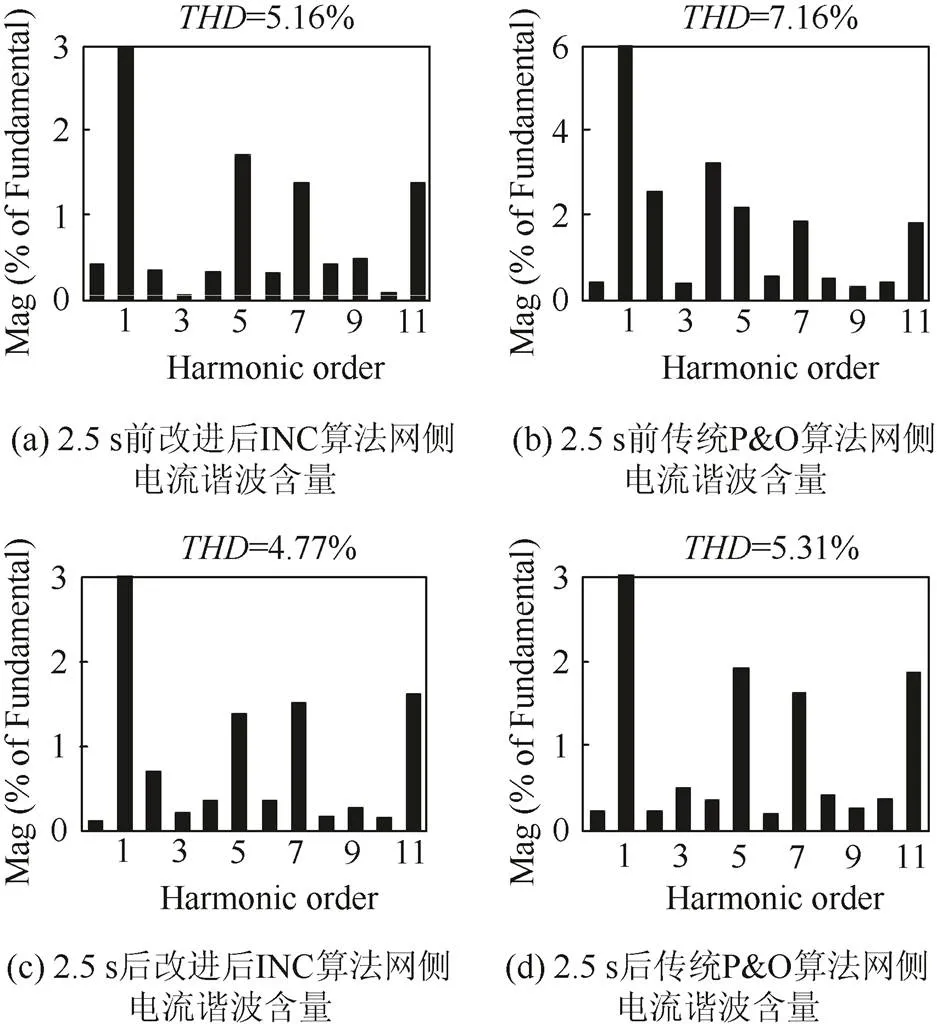
图13 改进后INC和传统P&O算法2.5 s前后网侧电流谐波含量对比

两种MPPT算法对系统统一控制的影响还会出现在随环境和负载切换的逆变器直流侧电压波形变化对比上。如图14所示，两种算法控制的直流侧电压波形都能在负载切换和光照变化的情况下基本保持稳定。在强光照的条件下，传统P&O算法控制的直流侧电压波形波动始终略大于改进后INC算法控制的直流侧电压波形，同时也验证了该改进策略的正确性和可行性。

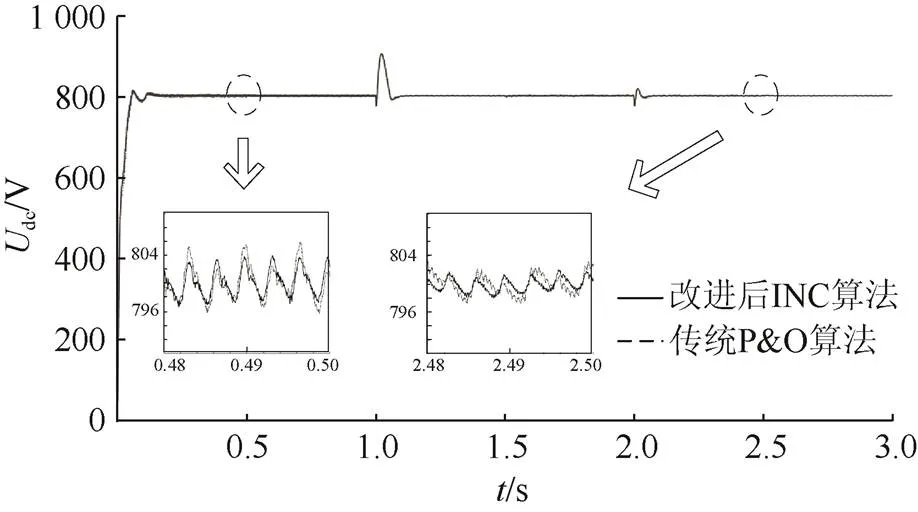
图14 改进后INC和传统P&O算法直流侧电压对比图

5 结论

本文基于L型滤波电路，通过优化三相光伏并网与有源滤波的统一控制策略，使系统在环境变化和负载切换中均能迅速准确地响应并治理谐波。其中，采用改进后分段式变步长INC算法迅速消除光伏电池输出电流振荡，有效抑制谐波检测电流的偏离，进而降低网侧电流谐波含量；调整逆变器容量分配和系统模式切换方案使其易于工程实现，均对优化光伏并网电能质量、降低谐波治理成本、提高光伏逆变器的设备利用率具有积极意义。

[1] 王飞, 余世杰, 苏建徽, 等. 太阳能光伏并网发电系统的研究[J]. 电工技术学报, 2005, 20(5): 72-74. WANG FEI, YU SHIJIE, SU JIANHUI, et al. Research on photovoltaic grid-connected power system[J]. Transactions of China Electrotechnical Society, 2005, 20(5): 72-74(in Chinese).

[2] 陈炜, 艾欣, 吴涛, 等. 光伏并网发电系统对电网的影响研究综述[J]. 电力自动化设备, 2013, 33(2): 26-32. CHEN WEI, AI XIN, WU TAO, et al. Influence of grid-connected photovoltaic system on power network[J]. Electric Power Automation Equipment, 2013, 33(2): 26-32(in Chinese).

[3] 侯庆庆. 基于MPC的三相离网逆变器控制方法的研究[D]. 合肥: 安徽大学, 2016(in Chinese).

HOU QINGQING. Study on control method of three-phase off-grid inverter based on MPC[D]. Hefei: Anhui University, 2016.

[4] 玄兆燕, 马振宇, 景会成, 等. 具有谐波和无功治理的LCL型并网逆变器研究[J]. 电力电容器与无功补偿, 2018, 39(5): 106-111. XUAN ZHAOYAN, MA ZHENYU, JING HUICHENG, et al. Study on LCL type grid-connected inverter with harmonic and reactive power control[J]. Power Capacitor & Reactive Power Compensation, 2018, 39(5): 106-111(in Chinese).

[5] 黄玉水, 吴永利, 周明建. APF在光伏发电系统中的应用与研究[J]. 电源技术, 2015, 39(11): 2441-2443. HUANG YUSHUI, WU YONGLI, ZHOU MINGJIAN. Application and research of active power filter on photovoltaic power generation system[J]. Chinese Journal of Power Sources, 2015, 39(11): 2441-2443(in Chinese).

[6] 马永翔, 王一君, 闫群民, 等. 基于HAPF的光伏微电网谐波抑制研究[J]. 可再生能源, 2018, 36(12): 1776-1780. MA YONGXIANG, WANG YIJUN, YAN QUNMIN, et al. Study on harmonic suppression of photovoltaic microgrid based on HAPF[J]. Renewable Energy Resources, 2018, 36(12): 1776-1780(in Chinese).

[7] 於锋, 胡国文. 具有改善电能质量的光伏发电并网控制器研究[J]. 低压电器, 2010(22): 21-24. YU FENG, HU GUOWEN. Study on control strategy for photovoltaic grid-connected generation with electrical energy quality improved[J]. Low Voltage Apparatusa, 2010(22): 21-24(in Chinese).

[8] 张贵涛, 龚芬, 王丽晔, 等. 光伏并网逆变器电能质量控制策略[J]. 电力科学与技术学报, 2017, 32(4): 50-56. ZHANG GUITAO, GONG FEN, WANG LIYE, et al. Power quality control strategy of photovoltaic grid-connected inverter[J]. Journal of Electric Power Science and Technology, 2017, 32(4): 50-56(in Chinese).

[9] 张国荣, 张铁良, 丁明, 等. 光伏并网发电与有源电力滤波器的统一控制[J]. 电力系统自动化, 2007, 31(8): 61-66. ZHANG GUORONG, ZHANG TIELIANG, DING MING, et al. Combined control of active power filter and PV grid connected generation[J]. Automation of Electric Power Systems, 2007, 31(8): 61-66(in Chinese).

[10] 汪海宁, 苏建徽, 张国荣, 等. 光伏并网发电及无功补偿的统一控制[J]. 电工技术学报, 2005, 20(9): 114-118. WANG HAINING, SU JIANHUI, ZHANG GUORONG, et al. Unified control of PV grid connected generation and reactive compensation[J]. Transactions of China Electrotechnical Society, 2005, 20(9): 114-118(in Chinese).

[11] 黄辉, 黄玉水, 王小明, 等. 三相光伏并网与有源滤波的统一控制仿真研究[J]. 电气传动, 2014, 44(10): 27-30. HUANG HUI, HUANG YUSHUI, WANG XIAOMING, et al. Unified control simulation for three-phase photovoltaic grid-connected and APF[J]. Electric Drive, 2014, 44(10): 27-30(in Chinese).

[12] 张杰, 郭晓霞, 赵威. 光伏并网与有源滤波统一控制系统的研究[J]. 现代电力, 2015, 32(1): 64-69. ZHANG JIE, GUO XIAOXIA, ZHAO WEI. Unified control of grid-connected photovoltaic and active power filter[J]. Modern Electric Power, 2015, 32(1): 64-69(in Chinese).

[13] 王震. 具有APF功能的三相光伏并网发电系统的设计与研究[D]. 成都: 电子科技大学, 2016.

WANG ZHEN. The design and research of three-phase photovoltaic grid power system with APF function of APF[D]. Chengdu:University of Electronic Science and Technology of China, 2016(in Chinese).

[14] 孔维功, 李丽荣. 基于有源滤波的并网逆变器仿真研究[J]. 实验室研究与探索, 2017, 36(7): 103-107. KONG WEIGONG, LI LIRONG. Simulation research on the grid-connected system inverters based on active power filter[J]. Research and Exploration in Laboratory, 2017, 36(7): 103-107(in Chinese).

[15] 张杰, 赵威, 姚凯, 等. 融合电能质量控制的光伏逆变技术研究[J]. 电源技术, 2015, 39(10): 2189-2192. ZHANG JIE, ZHAO WEI, YAO KAI, et al. Research on functions of power quality control of photovoltalic grid-connected technology[J]. Chinese Journal of Power Sources, 2015, 39(10): 2189-2192(in Chinese).

[16] 李孟帅. 光伏发电MPPT算法及控制研究[D]. 淮南: 安徽理工大学, 2019.

LI MENGSHUAI. Research on MPPT algorithm and control of photovoltaic power generation[D]. Huainan:Anhui University of Technology, 2019(in Chinese).

[17] 刘晓博, 郭中华. 光伏最大功率点跟踪变步长电导增量法的算法优化[J]. 科学技术与工程, 2018, 18(13): 61-67. LIU XIAOBO, GUO ZHONGHUA. Algorithm optimization of variable step-size incremental conductance method for photovoltaic maximum power point tracking[J]. Science Technology and Engineering, 2018, 18(13): 61-67(in Chinese).

Research on Unified Control Strategy of Photovoltaic Grid-connected Generation and Active Power Filter

WU Simeng, HAO Zhenghang, LEI Tinghao, CHEN Zhuo

(The Electrical Engineering College, Guizhou University, Guiyang 550025, China)

The unified control strategy of the photovoltaic grid-connected generation and active power filter can solve the problems of low equipment utilization rate, single function and high cost of active filter functionof photovoltaic power generation system when the illumination is insufficient. But the traditional control of perturbation and observation method finds the maximum power point by applying the disturbance voltage. The output current of the photovoltaic modules will continue to oscillate, which will affect the accuracy of the harmonic compensation current from detection to output. Different from the traditional method, under the unified control strategy of photovoltaic grid-connected generation and active power filter, a new improved piecewise variable-step incremental conductance method is adopted to eliminate the output current oscillation of photovoltaic cells; reinforce the specific odd harmonic current compensation and design the system working mode to improve the power quality. The proposed control strategy is simulated and verified by MATLAB/SIMULINK under the condition of continuous change of environment and load, and the results show the effectiveness of the improved control strategy.

photovoltaic grid-connected generation; active power filter; unified control strategy; piecewise variable-step incremental conductance method; the special odd harmonic compensation

10.3969/j.ISSN.1672-0792.2021.02.002

TM711

A

1672-0792(2021)02-0009-08

2020-10-10

贵州省科技计划项目（[2018] 5615）

伍思孟（1994—），男，硕士研究生，主要研究方向为电力电子与电力传动；

郝正航（1972—），男，教授，主要研究方向为智能电网及其仿真技术；

雷廷浩（1994—），男，硕士研究生，主要研究方向为智能电网及其仿真技术；

陈 卓（1980—），女，教授，主要研究方向为电力系统稳定与控制。

郝正航