混合高斯噪声背景下基于多目标优化的节点选择方法

闫青丽 陈建峰

①(西安邮电大学计算机学院 西安 710121)

②(西北工业大学航海学院 西安 710072)

1 引言

由于声音具有不受光线和能见度限制，隐蔽性强、不易受到电子干扰以及容易获取等优点，声源定位技术被广泛应用于工业自动化、医疗护理、智能交通、智能安防以及抢险救灾等民用领域。根据用来估计声源位置的信号参数，目前，常见的声源定位方法有3种：(1)基于信号到达方向角(Angle Of Arrival, AOA)的定位方法；(2)基于到达时间(Time Of Arrival, TOA)或基于到达时间差(Time Difference Of Arrival, TDOA)的方法；(3)基于接收信号能量(Received Signal Strength, RSS)的方法。由于每个节点单独执行AOA估计，不同节点处的信号不需要同步。且AOA计算原理和方法非常简单，因此，AOA定位技术得到广泛的关注和研究[1–4]。

理论上传感器节点越多定位性能越好，对于分布式的定位系统而言，使用全部的传感器节点可能会带来过度的数据冗余，而且传感器节点越多传感器能量和通信开销越大。另外，节点始终处于工作状态会缩短系统的寿命，增加系统成本。选择部分传感器节点实现目标位置估计是延长系统生命周期、降低成本的一个有效方法。但传感器节点数量减少会使得对应的定位精度随之降低。因此，如何根据目标位置的先验信息来动态选择最优的节点，实现节点个数和定位性能达到一定的平衡状态，是实际应用过程中需要解决的一个问题[4–11]。

Ertin等人[4]通过计算互信息，即预测的目标状态和当前节点测量的相互信息来确定不同传感器的信息增益。Wang等人[5]提出了基于熵的节点选择方法，减少了计算复杂度。文献[6]提出了利用马氏距离来评估信息效用的测量方法。这种方法计算效率高，但只适用于测距传感器。Kaplan[7,8]提出了两种节点选择方法，一种是首先选择两个与声源位置不在同一条直线上的节点，然后利用贪婪算法逐个选择能够最小化均方差(Mean Square Error, MSE)的节点；另外一种是随机选择若干个节点，然后通过将剩余节点代替选择的节点，根据定位性能的改变状态来改进节点选择集。在定位性能约束条件下，文献[9]中针对非线性测量模型，提出了3种基于凸优化的节点选择方法。针对线性测量模型，文献[10]研究了相关噪声背景下的节点选择问题。郝本建等人[11]研究了基于TDOA定位技术的节点选择方法，通过将非凸问题转化为半正定规划问题，实现节点的选择。

近几年，由于定位系统的应用背景越来越复杂，当传感器节点存在一定不确性时的传感器节点选择问题也逐步受到关注[12–14]。Cao等人[15]研究了在不确定传感器网络中，分别利用互信息和Fisher信息作为性能指标时的节点选择问题。Zhao等人[16]研究了非视距传播环境中基于到达时间差的节点选择方法。

当各个节点的估计误差服从高斯分布时，基于互信息和Fisher信息矩阵的节点选择方法选择结果具有一致性。但是对于节点存在一定不可靠性的定位系统而言[17,18]，基于这两个准则的节点选择结果往往具有一定的差异性。如何综合考虑两种定位性能准则进行节点选择是目前研究中的空白。

2 AOA定位算法

基于AOA的定位技术通过估计声源到达节点的方向，然后利用三角定位法确定声源位置。假设声源真实位置为 x =[x,y]T，声源到各个节点的真实方向角(AOA)为 θi， 节点si=[xi,yi]T估计的声源到达角为。和θi存在如式(1)的关系

其中， θi=arctan((y −yi)/(x −xi)), ni为角度 测量误差，理想情况下，通常假设其服从高斯分布。当节点失效或受到脉冲噪声干扰时，ni不再服从简单的高斯分布，而是服从一种严重拖尾的分布。本文中用L项的高斯混合模型来表示节点的估计误差

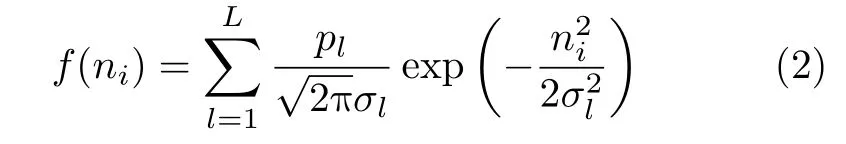
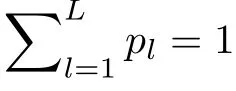
3 节点选择准则

3.1 贝叶斯Fisher信息矩阵

对于被动定位系统，声源的精确位置是未知的，但可以粗略预估目标可能出现的区域。假设已知声源的先验分布f(x)，对应贝叶斯Fisher信息(Bayesian Fisher Information, BFI)矩阵，BFI通常包含两部分

当目标位置的先验分布为f (x)时 ，Iprior可以表示为

由于Ii=∫(x)f(x)dx，条件信息矩阵为

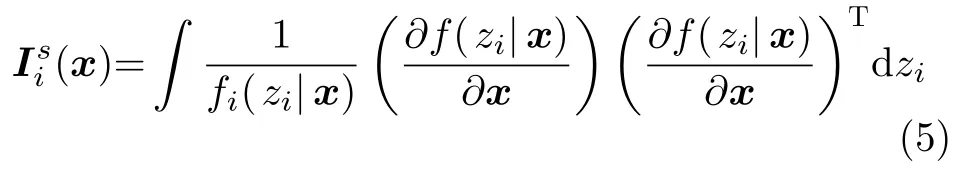
对于AOA定位问题，zi=θi(x)+ni,i=1,2,···,N，则条件概率密度函数为

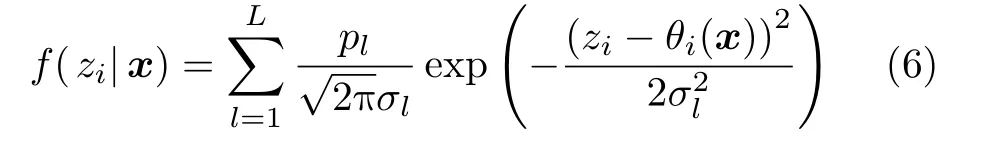
通过简单的计算可以得到

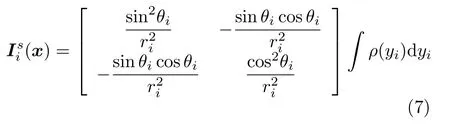
其中

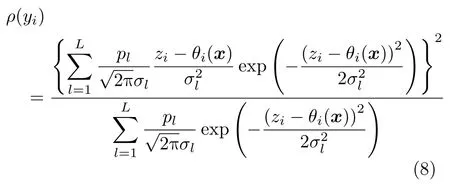
图1给出了当背景噪声保持不变，干扰噪声不断增大时的信息因子的变化趋势。从图1可以看出，当σ2/σ1≈1时，即估计误差服从高斯分布时，Iscalar达 到最大值，随着干扰噪声的出现，Iscalar减小。值得注意的是，FI信息因子并不是随着σ2/σ1的增大而单调减小，当 σ2/σ1<4时，FI的比例因子随着σ2/σ1的增大而减小。在这种情况下，干扰噪声只稍微大于背景噪声，很难识别此类干扰，因此信息因子会随着干扰项的增大而减小。当σ2/σ1≈4时，信息因子具有最小值。相反，当σ2/σ1>4时，FI的比例因子会出现轻微上升并逐渐趋于稳定的趋势，这是因为 σ2/σ1>4时，干扰项变得越来越明显，相对容易识别，干扰噪声的影响反而变小。

3.2 互信息

互信息(Mutual Information, MI)通过衡量x与zi的相关性，即评估不同的节点观测值所带来的关于目标位置x的信息，选择具有最大互信息值的节点，节点si的互信息可表示为

图1 信息因子与σ 2/σ1的关系

H(zi)为 预测的传感器节点测量值的熵，H (zi|x)实际上是对所有可能目标位置平均期望熵。与图1类似，这里观察MI与 σ2/σ1的关系，MI与σ2/σ1的关系如图2所示。从图中可以看出，MI随着 σ2/σ1的增大逐渐减小，后趋于稳定，并且 p1越大，互信息也越大，说明节点的不可靠性的确给MI带来了影响。

4 基于多目标优化的节点选择方法

4.1 基于多准则的节点选择方法

为了综合考虑不同的节点选择准则，本文考虑将BFI和MI同时作为优化的函数。由于在实际应用中，一般并不知道需要具体选择的节点数目。一种实际的方法是综合考虑节点个数和对应的定位性能来合理地选择传感器节点，因此，本文将选择的节点个数也作为一个优化目标。基于此，本节提出将节点选择问题表示为多目标优化问题。为了消除量纲的影响，本文对所有的目标函数进行归一化处理

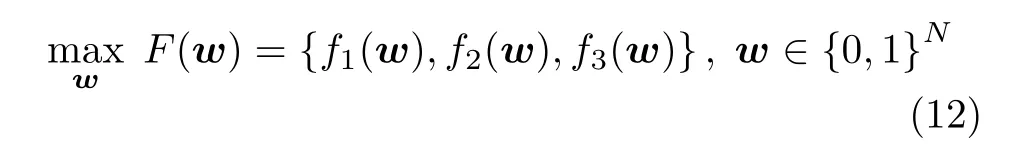
其中

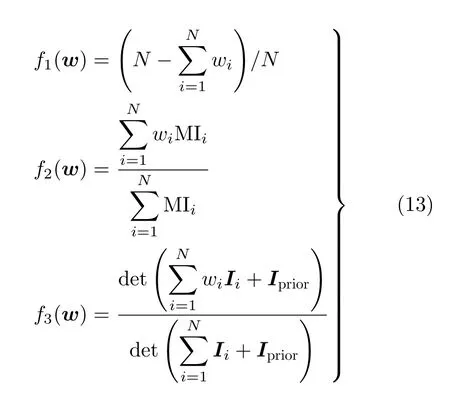
图2 互信息与σ 2/σ1的关系

第1个目标函数 f1(w)为选择的传感器节点个数，理想的情况是选择的节点个数越少越好，因此第1个目标函数实际是一个最小化问题。第2个和第3个目标函数分别为选择的传感器节点对应的MI和BFI；节点个数一定的时候，对应的MI和BFI越大越好，因此，后两个目标函数为最大化问题。为了将所有目标函数统一为最大化问题，本文将第1个目标函数转化为总的传感器节点个数N和选择的节点个数之间的差。理论上讲，传感器节点个数越多，所对应的定位性能越好，因此，式(12)中的3个目标函数是互相冲突的。为了求解式(12)所述的多目标优化问题，下文将利用多目标优化方法寻找使得3个目标函数达到某种平衡状态的最优解。

4.2 多目标优化方法概述

对于多目标优化问题(Multi-objective Optimization Problem, MOP)

目前，基于分解的多目标优化方法(Multi-Objective Evolutionary Algorithm based on Decomposition, MOEA/D)由于计算复杂度低，能得到较为均匀分布的Pareto最优解，其得到了较为广泛的应用[19]。本文采用MOEA/D的方法来解决节点选择中的多目标优化问题(MOEA/D based Sensor Selection, MOEA/D-SS)，其中利用切比雪夫法来实现多目标聚合。

4.3 基于与理想解相似的偏好排序技术的最终选择节点决策

值得强调的是传感器节点选择的最终目的是获得一组单一的选择结果，而多目标优化的结果是一系列的Pareto最优解，因此如何从这些候选解中选择最终的解是一个决策问题。在节点选择问题中，往往要在节点个数和定位性能之间进行权衡。对不同的定位系统，往往是人为地去设置性能需求，因此，不同的偏好或者需求要求人们选择不同的结果。基于此，本文利用与理想解相似的偏好排序技术(Technique for Order of Preference by Similarity to Ideal Solution, TOPSIS)[20]进行最终的决策。在介绍这两种方法前，首先对统一的符号进行定义：fij： 第i个解对应的第j个目标函数；Fij: fij归一化后的值； vij: fij或 Fij的权值；wj：第j个目标函数的权值。

根据TOPSIS，所选择的最优解应该到理想解(也称为正理想解)的欧氏距离最小以及到负理想解的欧氏距离最大。理想解是给定最优解中每个目标最佳值的组合(在最大化问题中就是最大值)。相反，负理想解是给定最优解中每个目标最坏值的组合。

步骤 1 构建归一化的K ×3目标矩阵

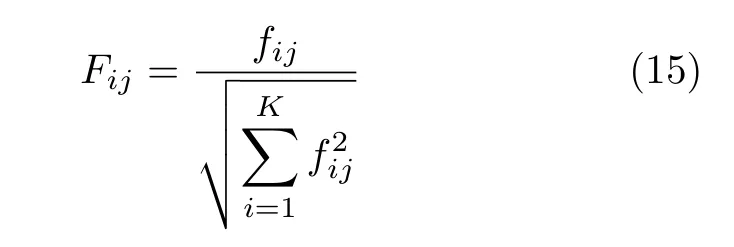
步骤 2 构建归一化的K ×3加权目标矩阵

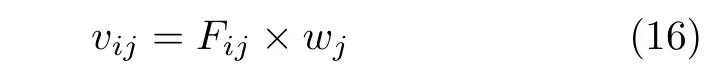
步骤 3 确定正理想解 A+，即为每个目标函数的最大值和负理想解 A−即为每个目标函数的最小值；

步骤 4 计算每个解到正理想解和负理想解的距离

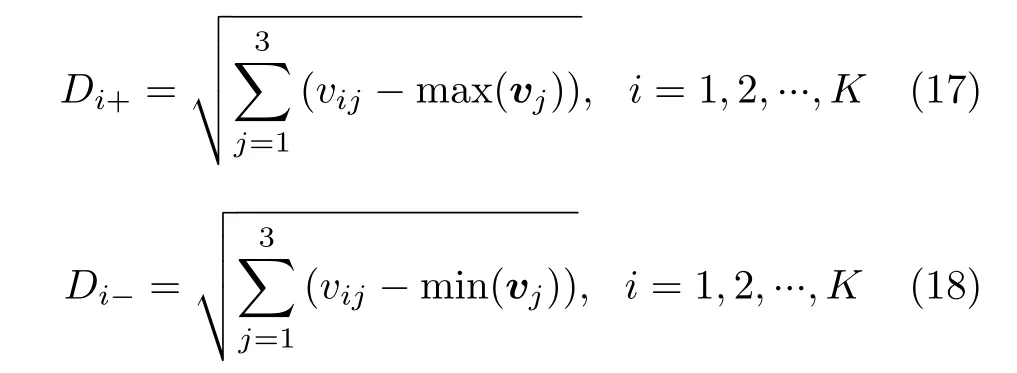
步骤 5 计算每个最优解的贴近度

具有最大值的最优解即为最终要选择的解。因此，根据MOEA/D求解的PS，应用TOPSIS技术即可进行最终决策。

4.4 算法复杂度分析

本文所提基于多目标优化的节点选择方法，首先需要计算两个性能参数。根据文献[5]，将目标先验分布和节点观测角度分别均匀分割为 n ×n个离散点时，N个节点的互信息计算复杂度为O(Nn4),Fisher信息矩阵的计算复杂度为O(4Nn4)。值得注意的是，互信息和Fisher信息矩阵计算完成后，在节点选择算法执行过程中可重复使用不必重复计算。

在MOEA/D的方法中，主要的计算成本在随机选择两个遗传算子的解，每计算一个目标函数，执行向量相乘的复杂度为O(N)，执行比较和赋值的复杂度为O(m)，因此，时间复杂度为O(mN)；计算T个解的切比雪夫值，每个计算步骤复杂度为O(mN)，总体复杂度为O(mTN)。因此，MOEA/D总体复杂度为O(mKTN)。

T O P S I S 算法，第1 步的计算复杂度为O(mK)，第2步执行了m次长度为K的向量与一个标量的乘积，其计算复杂度为O(mK)，第4步计算复杂度为O(2 m K), T O P S I S 算法复杂度为O(2mK)。

综上所述，本文节点算法的计算复杂度为O(4Nn4+ mKTN)。本文所提节点选择问题中有3个目标函数，因此m=3。

5 仿真结果

本文的仿真基于以下参数：25个传感器节点均匀地布放在 100×100 m2的测试区域内，如图3所示。每个节点都有已知的可靠概率。角度测量误差模型为混合高斯噪声，其中背景噪声和干扰噪声的标准差为σ1=0.5◦, σ2=30◦。假设目标的先验区域为a1≤x ≤b1,a2≤y ≤b2, 图3中菱形表示不同的(a1,a2) 值 ，且| b1−a1|=|b2−a2|=5。图3中圆圈表示传感器节点，其右侧的整数表示节点对应的索引值，下方的浮点数表述节点的可靠概率。为了简化计算，本文将目标的先验区域均匀网格化为50×50个点，将式(3)以及式(9)中的积分离散化为近似的求和计算。

5.1 基于MOEA/D的Pareto解

本文采用的多目标优化算法MOEA/D中采用遗传进化算法，其中选择单点交叉算子和标准的变异方法[20]；变异概率和交叉概率分别为1和1/N(N为传感器的节点个数)。每一个权向量的邻居规模大小为 T =20。种群规模大小为325。最大的进化次数为400。以第4个声源位置为例，本节将基于MOEA/D的优化结果与基于NSGA-II的优化结果进行比较，如图4所示。从图4中可以看出，基于MOEA/D的方法可以找到相对比较均匀的非支配解。相同的节点个数(即f1相同)时，选择不同的节点组合对应的BFI和MI也不相同。

5.2 不同目标位置区域的节点选择结果

为了直观地观察不同节点选择策略的选择结果的区别，图5显示了两个不同声源位置的节点选择结果。为了进行对比，本文分别利用文献[9]提出的基于凸优化的节点选择方法和文献[5]提出的基于MI的方法选择与MOEA/D-SS相同节点的个数。

图3 25个传感器节点布局

图4 基于MOEA/D和NSGA-II的Pareto解

从图5可以看出基于凸优化的选择方法往往选择距离声源位置较近的节点，即使它们具有较低可靠概率，而基于MI的方法总是选择具有高可靠概率的传感器。例如对于图5(b)所示目标位置，s19的可靠概率仅有0.35，但是距离声源非常的近，基于凸优化的节点选择方法选择了该节点，而基于MI的选择策略由于其较低的可靠概率而舍弃了该节点。这与文献[15]中的研究一致。通过综合考虑BFI和MI两种性能评估准则，本文所提节点选择方法舍弃掉接近声源位置但具有较低可靠概率的节点s9, s15, s23，反而选择了距离稍远但可靠概率较高的节点s5, s7, s22，这与MI的选择结果相似。但与MI不同的是MOEA/D-SS选择了距离声源非常接近的节点s19，这一点与BFI相似，因此，利用MOEA/D-SS选择方法会综合考虑MI和BFI两种性能指标来选择节点。结果还表明，一个好的选择策略非常重要，因为一个不同的传感器可以显著提高定位性能。

5.3 权值对选择结果的影响

若对于第i个目标位置，利用多目标优化方法及决策方法有ki个节点被选择，为了说明提出的基于两种性能指标的优化方法的优越性，下文利用基于MI的方法和基于BFI的方法分别选择ki个节点，然后利用文献[14]提出的基于迭代的重新加权的最小二乘法实现定位，最大迭代次数设为50次。对于每个网格点均进行1000次的独立重复试验，最终的每个网格点的RMSE的平均值作为定位性能指标。为了研究权重向量对选择结果的影响，图6绘制了不同权重向量下选择的传感器数量。

如图6所示，当选择的传感器节点个数的权重值较小时，表示与系统代价相比，定位性能更为重要，因此将选择更多的传感器来提高定位性能。当w=[0.4,0.45,0.15]时，对应的定位误差的平均RMSE如图7所示，从图7中可以看出基于MOEA/D-SS的节点选择策略选择的节点往往具有更好的定位性能。

5.4 节点估计误差对选择结果的影响

由4.2节可知， σ2与σ1的相对大小对信息因子Iscalar和 互信息值的影响不同，本节将通过仿真对σ2与σ1的相对大小对节点选择的影响进行分析。以第6个声源和第10个声源为例，当背景噪声固定为σ1=0.5◦，干扰噪声逐渐增大时，3种不同节点选择策略的定位结果的平均RMSE如图8所示。从图8中可以观察到对第6个声源，基于BFI选择的传感器节点往往比MI选择的节点具有更差的定位性能。对于第10个声源位置，BFI和MI选择的传感器节点在不同的干扰噪声时的定位性能不一样，并且不能简单认为哪一种性能选择准则更好，也说明了本文提出的基于多目标优化方法的必要性。图8表明对于两个声源位置，利用提出的多目标优化方法选择的传感器节点具有更稳定和更优的定位精度。

图5 不同声源位置时的节点选择结果

图6 TOPSIS中不同权值时选择的节点个数

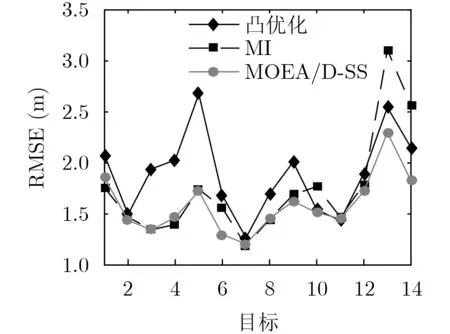
图7 不同目标位置的平均RMSE

图8 σ 2逐渐增大时第6个声源和第10个声源对应的定位误差

6 结论

为了解决节点选择不一致的问题，本文提出将不同的性能指标同时作为目标函数，利用多目标优化方法寻找使得这些优化目标函数达到一定平衡状态的解集，即Pareto最优解。并利用TOPSIS进行最终决策。仿真结果表明，利用多目标优化进行节点选择可以充分考虑节点的可靠概率和节点与声源的相对位置，选择的节点对应的定位性能优于只利用单一性能指标作为优化目标选择节点的定位性能。