一种类箕舌线函数的变步长归一化自适应滤波算法

火元莲 龙小强 连培君 王丹凤

(西北师范大学物理与电子工程学院 兰州 730070)

1 引言

随着滤波算法的不断更新迭代，目前自适应算法已经成为信号处理和现代通信等领域的重要组成模块，常应用于信道均衡、回波消除、自适应控制、波束形成、噪声抵消和系统辨识等领域[1—9]。

在众多自适应滤波算法中，由Widrow和Hoffman于1960年提出的自适应滤波算法(Least Mean Square, LMS)[10,11]因其原理简单，便于实现，鲁棒性以及稳定性好等特性得到了大量的关注，继而归一化最小均方滤波算法(Normalized Least Mean Square, NLMS)[12]也得到了发展。但LMS和NLMS都存在相同的缺陷，即对收敛速度和稳态误差两者不可兼得，所取步长越大，收敛速度越快，但稳态误差也随之增大；步长越小，稳态误差变小，但收敛速度变慢。为了改善这一不足，变步长滤波算法被相继提出[13—22]。

而变步长自适应滤波算法的基本原则是步长因子µ (n)随着算法做动态调整[13]，以便保证在算法收敛初期，提供较大的步长取值使算法有较快的收敛速度；在算法收敛完成阶段，提供较小的步长取值使算法的稳态误差变小，有更好的稳定性。如覃景繁等人[14]提出的基于Sigmoid函数的变步长LMS算法(Sigmoid Variable Step Least Mean Square,SVSLMS)，兼顾了收敛速度与稳态误差间的矛盾，但在算法收敛阶段，误差e (n)的微小变化都会引起步长因子 µ (n)较大变化，从而影响算法的稳态误差；在Sigmoid函数的基础上，刘宪爽等人[15]给出了一种改进的双Sigmoid函数变步长自适应算法，该算法的稳定性和实际应用时的准确度在传统SVSLMS算法基础上得到了提升，但其收敛速度和稳态误差却也随之下降；事实上，在基于Sigmoid函数的变步长自适应算法中，由于求步长因子µ(n)时需要进行指数运算，用查表法很繁琐而且占用硬件存储空间。为此基于箕舌线函数(阿格尼丝箕舌线函数“the witch of Agnesi or Versoria”，中文简称为箕舌线函数“Versoria”)的变步长自适应滤波算法得到了发展，如邓江波等人[16]提出的基于箕舌线的变步长LMS自适应算法，改善了SVSLMS算法收敛速度、稳定性以及跟踪速度等性能，但在时变环境下跟踪能力和收敛速度性能仍然不足；为再次提升性能，韩允等人[17]搭建了新的步长调整函数，提出了基于箕舌线的变步长归一化最小均方算法，该算法很好地协调了系统的抗干扰性能和快速跟踪性能间的矛盾，但却加大了系统的失调量。所以如何在收敛速度、稳态误差、计算量、跟踪速度等各方面做到兼顾是自适应滤波算法设计中的关键。本文算法的主要思想是：借鉴箕舌线函数计算复杂度小、易于实现、在稳态阶段步长因子很小且变化不大等特性，采用类箕舌线函数对步长因子µ (n)进行调整，在大大增强算法稳定性的同时大幅度提升算法的收敛速度、跟踪速度等特性。

2 本文算法原理及性能

2.1 算法原理

图1 类箕舌线函数曲线调整过程曲线图

从图1可以看出，曲线2和曲线3都符合自适应滤波算法的步长调整原则，即在算法初期(算法收敛初始阶段)，步长调整函数为算法提供较大的步长取值，以提高算法的收敛速度，使其快速过渡到算法收敛完成阶段；在收敛完成阶段，提供较小的步长取值，使算法在该阶段保持更好的稳定性。式(1)可以看作一种新的非线性步长因子µ (n)调整函数模型，再引入曲线调整参数 α, β 和γ 控制步长的大小等[18]，得到了类箕舌线函数模型

其中，参数α >0 控制函数形状，参数β >0控制函数的幅值， γ为算法收敛速度控制参数。由此，本文类箕舌线的归一化变步长自适应滤波算法为

其中，X (n)是 第n 时 刻的输入信号矢量；e (n)是误差信号； d (n) 是 期望输出；W (n)是n 时刻的滤波器抽头系数； µ (n)是 第n 次迭代时的步长；XT(n)是输入信号X (n)的 转置矩阵；XT(n)X(n)是归一化函数，可以看作n 时刻的信号能量；δ 为一个极小的数，用来微调归一化的值，可忽略不计。

2.2 算法性能分析

为了更好地分析步长调整函数模型中参数 α，β对步长因子波动和参数γ 对算法收敛速度的影响，下面将分别对各参数的取值原则和范围进行讨论，为了直观有效地分析，在步长曲线调整中取γ =0 时讨论 α， β 的情况，图2(a)为α 相 同、β 不同时步长因子µ (n)与 误差e (n)调整曲线图；图2(b)为α不 同、β 相同时步长因子µ (n)与 误差e (n)调整曲线图；图3为参数γ 取不同值时的算法收敛速度图。

图2(a)中3条曲线是 β分别取0.002, 0.005,0.010(α =8)时所对应的步长调整曲线，从图中可以看出， β取值越小，步长因子在误差接近零处变化越小，但在算法收敛初期不能够为算法提供较大的步长取值，算法收敛速度较慢；当 β取值较大时，能够提供较大的步长取值使算法有较快的收敛速度，但同时步长因子在误差接近零时受误差的影响也将增大，综上 β的取值范围应在0.005～0.500，在本文中取β =0.010，此时算法的收敛速度、跟踪能力等性能表现最优。图2(b)中3条曲线是α 分别取2, 4, 8( β =0.010)时所对应的步长调整曲线，从图中可以看到，当 α越大时，为算法在收敛初期提供的步长取值越大，但算法在收敛完成阶段的稳定性下降；当 α越小时，算法在收敛完成阶段越稳定，但算法的收敛速度较慢；考虑到均衡稳定性与收敛速度，在本文中取 α =4 。图3为参数γ 对算法收敛速度的影响效果图，可以看出， γ越大时算法的收敛速度越快，但 γ也不宜过大，γ 过大时算法的稳态误差增大，会使 γ对算法收敛速度的控制作用大大下降， γ的选取可以在实际应用时根据情况而定，需要较快的收敛速度时取较大值，对收敛速度需求不高时则选取较小的值，为兼顾收敛速度与稳态误差，在本文中取γ =0.20。

2.3 几种算法模型性能对比分析

为有效直观地验证本文算法的性能，现将本文算法步长调整函数模型同SVSLMS算法、文献[15]算法、文献[16]算法、文献[17]算法进行比较。图4为5种算法的步长调整曲线图，从图中可以看出，5种算法的步长调整函数模型都符合变步长自适应滤波算法步长因子的调整原则，即在算法收敛初期步长取值较大，使算法有较快的收敛速度，在算法收敛完成阶段(误差 e(n)接近零处)，步长变化较小，使算法在稳态阶段保持较好的稳定性。

但在图中也可以看到，文献[16]算法步长调整函数模型在算法收敛初期的步长取值是最小的，这使得该算法收敛速度较慢，本文算法步长调整函数模型提供的步长取值最大(算法收敛初期)，确保算法有较快的收敛速度，使算法能够快速地过渡到稳态阶段；在算法收敛完成阶段(误差接近零处)，本文算法步长因子也能够保持较小的变化，使算法在稳态阶段保持较好的稳定性，所以本文提出的类箕舌线函数模型表现更优。

µ(n) e(n)图2 步长因子 与误差 调整曲线图

图3 γ不同时算法收敛速度图

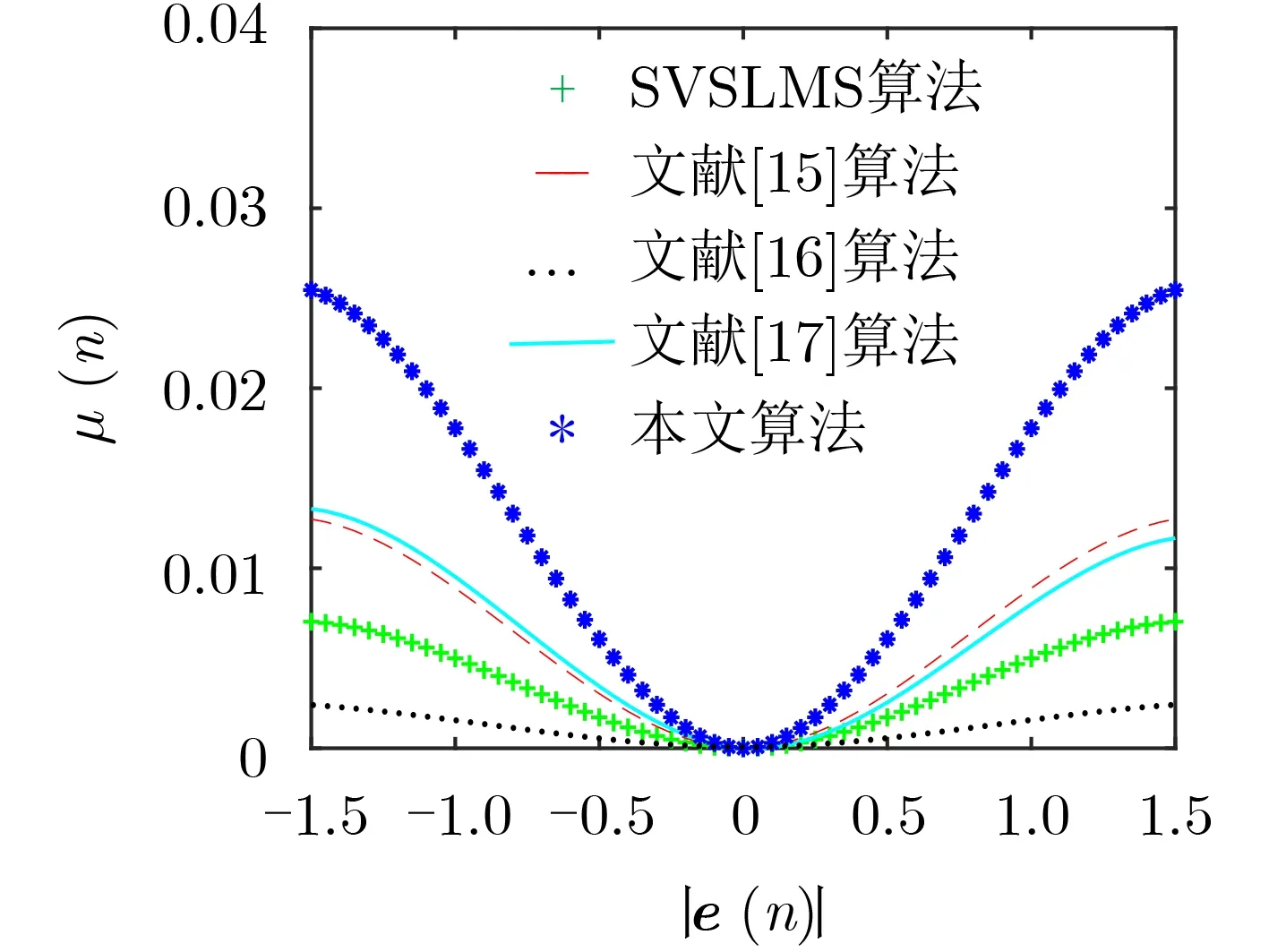
图4 5种算法步长调整曲线图

3 模拟仿真结果与对比分析

为了检验本文算法的收敛速度、跟踪能力等性能表现以及参数 α, β 和γ 对算法收敛性能的影响，基于Matlab平台对算法进行模拟仿真，实验仿真条件同文献[14]：(1) 自适应滤波器阶数 L=2;(2) 未知系统的FIR系数为 W∗=[0.8,0.5]T，在第500个采样点时刻未知系统发生时变，系数矢量变为W∗=[0.4,0.2]T; (3) 参考输入信号X (n)是零均值，方差为1的高斯白噪声；(4) v(n)为 与X (n)不相关的高斯白噪声，其均值是零，方差为σv2=0.04。分别做 200次独立的仿真，采样点数为 1000，然后求其统计平均，在不同信噪比背景下得出学习曲线。

图5为5种算法均方误差(Mean Square Error,MSE)变化曲线对比图，从图中可以看出在3种噪声背景下(信噪比(SNR)分别为10, 20, 30)，文献[16]中算法的收敛速度最慢，本文算法收敛速度最快；而且本文算法在收敛完成阶段也能够保持较小的均方误差以及更好的稳定性。

为了对比检验本文算法同其它4种算法在面对时变系统以及不同噪声背景下的跟踪性能，同等仿真条件下，算法在迭代到500次时未知系统发生时变，图6为在不同信噪比背景下5种算法面对时变系统时的跟踪能力曲线图。

从图6可以看出，在不同信噪比背景下，当系统发生时变时文献[16]中算法的跟踪能力较差，本文算法在5种算法中表现最好；且随着信噪比增大，这一优势更为明显。为了进一步证明本文算法的良好性能，对5种算法在不同信噪比条件下完成收敛过程的次数也进行了比较，如表1所示。

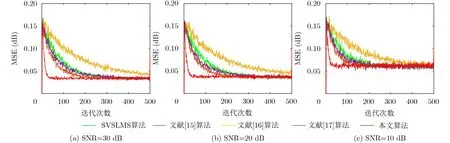
图5 不同信噪比背景下5种算法MSE对比图

图6 不同信噪比背景下5种算法面对时变系统时的跟踪性能对比图

表1 不同信噪比下算法收敛次数比较

4 结束语

本文提出了一种类箕舌线函数的变步长归一化自适应滤波算法，其算法思想是采用类箕舌线函数来代替Siogmoid函数作为步长迭代公式，引入基于相关误差的变步长调整原则。改进后的算法兼顾了收敛速度、稳态误差、跟踪性能、计算复杂度等性能间的矛盾，相比于SVSLMS算法、文献[15]算法、文献[16]算法、文献[17]算法，本文算法有更快的收敛速度、更好的跟踪能力以及较小的稳态误差和较强的鲁棒性。