数学建模活动“教”“学”“评”一致的实践与思考

2021-03-17黄炳锋

福建基础教育研究 2021年2期

黄炳锋

（福州第三中学，福建福州 350003）

随着教育部制定的《普通高中数学课程标准（2017 年版）》（下文简称“《课标（2017 年版）》”）的发布，数学核心素养被广为推介，学科核心素养是育人价值的集中体现，高中数学课程如何落实以学科核心素养为纲，引发热议.数学建模是高中数学学科六大核心素养之一，而“数学建模活动与数学探究活动”又是数学课程内容的四条主线之一，作为核心素养的“数学建模”与课程内容的“数学建模活动”有何区别，“数学建模素养”与“数学建模活动”有何联系，“数学建模活动”如何开展、评价，核心素养是可教、可学、可测评的，“数学建模活动”如何做到“教”“学”“评”一致等问题，引起关注与思考.本文拟以《普通高中教科书·数学（人教A 版）》必修一的数学建模活动“建立函数模型解决实际问题”为例，从教学建议、学法指导与评价实例三个角度加以阐述.

一、数学建模活动辨析

（一）数学建模活动是数学课程新增内容

与《普通高中数学课程标准（2003 实验版）》（下文简称“《课标（实验版）》”）相比，《课标（2017 年版）》将“数学建模活动与数学探究活动”作为一条主线，纳入课程内容，设置了教学课时，设计了评价方式，并要求将结果放入学生综合评价档案袋中，因此，“数学建模活动与数学探究活动”被称为新增内容.［1］但实际上，数学建模活动并非本轮课改首次提出.

上一轮课改《课标（实验版）》在“课程基本理念”中就提出“倡导积极主动、勇于探索的学习方式”，通过设立“数学探究”“数学建模”等学习活动，培养学生形成“积极主动的、多样的学习方式”，从而“激发学生的数学学习兴趣”，在学习过程中，养成“独立思考、积极探索的习惯”.在“内容标准”中专门阐述了“数学探究、数学建模、数学文化”的教学要求，给出教学建议.

可以肯定，上一轮课改《课标（实验版）》的实施，已经为《课标（2017 年版）》增加“数学建模活动与数学探究活动”为主线内容做了必要的准备.

（二）数学建模活动是四条主线内容之一

《课标（2017 年版）》将“数学建模活动与数学探究活动”与函数、几何与代数、概率与统计合并，设计为四大主题，贯穿于必修、选择性必修和选修课程的学习中，但“数学建模活动与数学探究活动”主题与其他主题在“内容要求”“教学提示”与“学业要求”上的阐述均有明显差异，其他主题在“内容要求”上，按单元划分，列出主题的教学核心内容，提出单元的教学目标，而“数学建模活动”在“内容要求”上并没有列出“核心内容”，只给出数学建模活动的内容本质和基本过程；在“教学提示”上，不是结合具体单元内容给出提示与建议，而是以课题研究过程中的环节给出建议与要求；在“学业要求”上，不是列出单元学习达成目标与要求，而是给出学业评价的方法，要求学生经历数学建模活动的全过程，完成课题研究.

由此可见，虽同为主线，数学建模活动与其他主线不同，数学建模活动没有安排核心内容，这意味着，这条主线内容的学习，不具体依托某个知识与技能，也可以说依托所有其他主线的内容进行数学建模主题的学习，教学重在过程与方法；给出的“教学提示”与“学业要求”也突出了“过程与方法”的评价.

（三）数学建模活动与数学建模素养关系

数学核心素养都可以从“概念内涵，学科价值，具体内容，学生表现，水平层次”等五个方面加以阐述，数学建模核心素养也是如此.

从素养的角度看数学建模，应注意“概念内涵”所揭示的数学建模的属性，把握其在“属性”上的定位.有三层含义：第一，数学建模包括了对现实问题的数学抽象；第二，数学建模需要用数学语言表达实际问题；第三，数学建模关键是用数学方法构建模型解决问题.结合聚焦学生数学学科核心素养的外显性行为（过程、步骤）的描述，不难看出，数学建模聚焦学生数学学科核心素养的几个关键环节：基于现实情境与数学抽象，构建数学模型，经历“发现问题—提出问题—分析问题—解决问题”的过程，进而发展“四能”（发现问题能力、提出问题能力、分析问题能力、解决问题能力），从而达到“三会”（会用数学的眼光看、会用数学的思维想、会用数学的语言表述现实世界）.基于上述分析，数学建模素养的内涵是极其丰富的，它与其他五个数学学科核心素养直接关联.数学建模素养不仅体现在解决一个数学应用的问题，而且还蕴涵着方法、思想、价值判断与选择，乃至数学的精神与解决问题的态度.

数学建模活动是一类综合实际活动，是基于数学思维和数学视角，“对现实问题进行数学抽象”“用数学语言表达问题”“用数学方法（主要是模型思想）解决实际问题”的过程之统称.《课标（2017 年版）》指出，数学建模活动主要包括“发现问题”“提出问题”“分析问题”“构建模型”“确定参数”“计算求解”“验证结果”“改进模型”“解决问题”等环节.从过程可见，数学建模活动需要数学建模核心素养的强力支持.

从活动的角度看数学建模，应注意“活动内涵”所揭示的数学建模的特点，应以课题研究的形式开展，并把握其在“内容”上的定位：第一，层次上可分为“了解数学概念的背景，重要结果直接应用，数学结果综合应用，数学建模”等，并逐级提升；第二，认识上可从“了解数学建模”“数学建模主要步骤”“数学建模主要过程”到“实践数学建模活动”逐步深入；第三，过程上可遵循课题研究的四个环节，如图1.

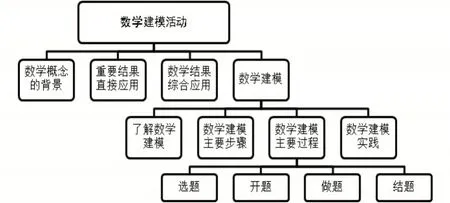
图1

比较数学建模素养与数学建模活动可以看出，数学核心素养是从学科角度提出的课程目标，可分解到教学目标，形成和发展数学建模核心素养需要结合各主线内容，数学建模核心素养可以教学，可以习得，也可以测评，形成并发展数学建模核心素养的渠道不止于数学建模活动，评价数学建模核心素养也与其他数学核心素养应用，可以按“情境与问题”“知识与技能”“思维与表达”“交流与反思”等四个方面，并分为三个水平执行；而数学建模活动是从课程角度提出的学习任务，它可以在活动中提升“四能”，养成“三会”，促进数学建模核心素养的形成与发展，数学建模活动亦可教可学，评价的关键是过程与方法.

二、数学建模活动“教“学”“评”过程例析

（一）整体设计，分层实施主题教学

数学建模活动贯穿高中数学必修课程与选择性必修课程全过程，数学建模活动的教学不能仅依靠划定的几个课时，而应全盘考虑.数学建模活动具有综合性强，数学建模素养与其他5 个核心素养也是联系紧密、相互交融，所以数学建模活动的教学需要一个渐进的而又有层次的整体设计，并借助主题教学实施，从数学知识的直接应用与渗透到完整数学建模活动的实施，以“建立函数模型解决实际问题”为例，可设计如下渐进的层次.

第一，引入实际情境（如函数概念的四个实例），帮助学生理解函数概念，在概念教学中提升并发展数学抽象等核心素养；

第二，直接套用实际情境中提供的函数式、公式等计算有实际意义的结果（如函数值，函数的表示），在例题教学中提升并发展数学运算等核心素养；

第三，间接套用实际情境中提供的概念式、公式等计算有实际意义的结果或者解释、说明、得到结果的实际意义（如函数的应用一），在例题教学中提升并发展数学抽象、数学运算等核心素养；

第四，在实际问题中，引领学生完成数学化的、简单具体的数学应用（如函数的应用二的4 个实例）；

第五，在实际情境中，引导学生自主完成数学化的、简单具体的数学应用（如第四章小结，复习题）；

第六，教师提供实际问题情境，学生自主发现并提出问题，在教师指导下学生完成“建立模型”和“模型求解”的主要过程（如数学建模活动“建立函数模型解决实际问题”中的建模实例）；

第七，学生部分自主（发现提出问题，模型的选择和建立，求解模型，给出模型结果的解释）、教师部分参与（给予指导和帮助），完成数学建模活动的全部过程（选题、开题、做题、结题）（如可在数学建模活动中继续补充一些实例）；

第八，全过程、全自主（自主决定是否寻求教师的帮助）的数学建模活动（如数学建模活动中开展的课题研究）.

日常教学中，注重在函数主线中对“数学建模素养”的逐步渗透，要有意识地达到第一、二、三、四的层次要求，在章节复习中提升到第五的要求，第六、七、八是数学建模活动的专项要求，可分散难点，逐步解决“数学建模活动”的关键环节，根据学生实际情况，选择做到某层次（如达到第六也可）.

（二）借助工具，化解收集数据困难

数学建模活动的实例教学，在数据收集环节，由于工具缺乏等原因，收集数据成为难点，但这个环节不能少也不能由教师代办，应组织学生以“小组合作参与全部流程、分工完成”的形式，因地制宜地开展教学活动.为适合不同学校学生的情况，教材提出“我们可以利用秒表、温度计等工具”，但实际上茶水温度变化太快，利用“普通工具+人工记录”的方法会有很大误差，因此教材也提示“若用计算机、数据采集器、温度传感器等信息技术更好”，鼓励融合使用信息技术支持数据收集工作.实际教学中，我们用空调进行室温调节，保证实验环境室温保持25℃；用开水冲泡相同数量的茶叶，保证茶水的品质一样，而且起始温度都能略超过85℃；用相同的容器盛茶水，保证茶水总水量不变；用能自动记录数据的温度传感器收集茶水水温与相应时间，并且设定记录间隔时间分别为10s，20s，…，60s，…经过多次实验，结合多次实验结果分析数据，我们发现每隔1min 记录的数据能较好地通过散点图反映出函数模型，于是取多次实验的数据进行均值、四舍五入处理，得到一组数据.

这里有几点需要特别说明：

第一，收集数据是必要的，需要学生参与收集数据的实践，学生重在参与数据收集的过程，数据有误差不影响数学建模活动的开展，但为了体现科学精神，可以提出“如何保证收集的数据更精确”等问题供学生思考；

第二，实验环境室温不一定恰好保持25℃，在问题呈现时，改变室温条件与相应的函数模型的参数即可；

第三，影响茶水温度变化的因素很多，比如空气湿度、大气压、茶水容器等，为简化数学建模活动，我们只考虑一般情况下，茶水温度与时间的关系，教学时不必过多涉及其他因素，干扰教学进程；

第四，实验环境、容器形状、不同茶叶等影响，数据可能与教科书不一致，不同小组也可能不一致.

（三）融合技术，解决建模关键环节

分析数据、建立模型与检验模型是实例教学的关键环节，因为这是数学建模活动中确定函数模型的基本步骤.通过观察发现，散点图的分布状况呈递减状态，学生可能会提出各种递减函数作为模型，而选用y=kax+b函数模型的理由，教材已经给出：观察散点图的分布状况，并考虑到茶水温度降至室温就不能再降的事实，可选择函数y=kax+25（k∈R，0＜a＜1，x≥0）来近似刻画茶水温度随时间变化的规律.实际教学中，可利用信息技术进一步引导学生选用其他几个基本初等函数模型进行拟合，并判断拟合效果，从而找到合适的函数模型.以教科书提供的数据为例，不同的函数模型拟合情况如下：

用一次函数f（x）=a+bx拟合，函数关系式为f（x）=83.6219-3.8874x，从相关指数R2=0.9820（图1-1）、散点图（图1-2）与残差图（图1-3）可以看出吻合程度较好.

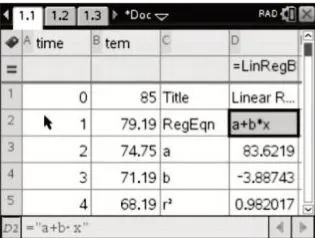
图1-1

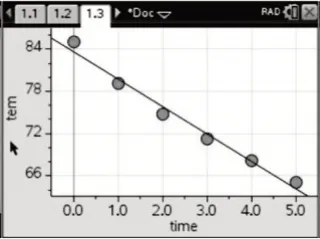
图1-2

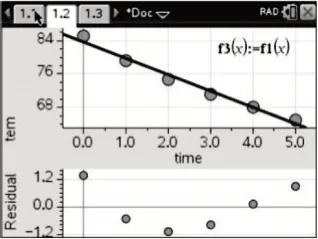
图1-3

用二次函数f（x）=ax2+bx+c拟合，函数关系式为f（x）=0.3457x2-5.6160x+84.7743，从相关指数R2=0.9986（图2-1）、散点图（图2-2）与残差图（图2-3）可以看出吻合程度比一次函数拟合要好.

图2-1

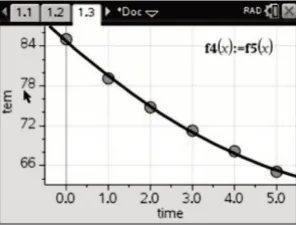
图2-2

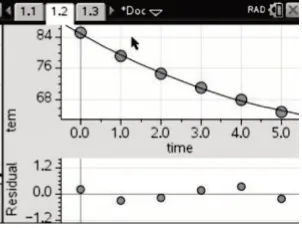
图2-3

用指数型函数f（x）=a×bx拟合，函数关系式为f（x）=83.8891×0.9490x，从相关指数R2=0.9910（图2-1）、散点图（图2-2）与残差图（图2-3）可以看出吻合程度很高.

图3-1

图3-2

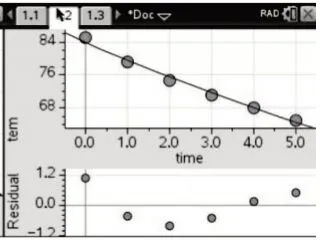
图3-3

用指数型函数f（x）=a×bx+25 拟合，函数关系式为f（x）=59.0532×0.9239x+25，从相关指数R2=0.9943（图2-1）、散点图（图2-2）与残差图（图2-3）可以看出吻合程度更高.

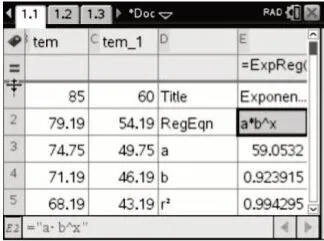
图4-1

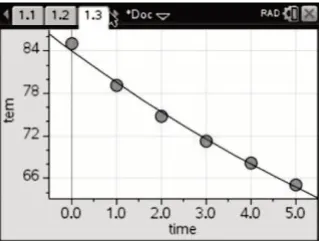
图4-2

图4-3

注：若经过更多数据拟合验证，可发现指数型函数f（x）=a×bx+25 拟合相关指数大于二次函数f（x）=ax2+bx+c拟合相关指数，且在四种效果中最佳.

教学中还应注意，选择拟合函数模型y=kax+25 之后，教科书在参数k与a值的确定方法上并不相同.k值的确定用的是起始状态的实际情况，即当x=0 时，y=85，解得k=60.尽管a的值也可以由一对（x，y）唯一确定，但教科书并不直接用表1 的一组数据代入求a，而用多组数据的比的均值求a，像这种采用平均值作为衰减比例来建立函数关系式的方法，在解决实际问题中不仅常用，而且与k值的确定一样具有统计意义.教科书在边框位置提出是否有差异的思考，教学时可作如下引导：事实上，根据数理统计学常识，要分析的随机变量越少越好，而每个变量获得的样本信息越多越好.因为随机变量越少，分析的过程就会越简单，而样本容量越大，分析的结果就会越可靠.［2］根据这一常识，就不难理解教科书在k值的处理上，是希望减少要分析的随机变量；a值的确定上用了多个数据，而用这些数据的平均数作为这些数据的代表，是期望其与各个数据方差是最小，模型的吻合程度更高.

三、数学建模活动的开放与过程性评价

数学建模活动的评价检测还在实践并积极探索中，考查数学建模素养的试题也不断涌现，本文以两个实例说明数学建模的“评”与“教”“学”是一致的.

例1 网上购鞋常常看到“脚长与鞋号对应表”，如下.

（1）据此你能提出什么问题？

（2）某篮球运动员的鞋号为53，你能想办法推测他的大致身高吗？

评析：本题根据提供的数据考查数学建模活动中的若干“环节”.数学建模活动的一个基本环节就是提出问题，“提出问题”的层次能反映数学建模素养的水平，如数据之间一般化、规律性结论的发现就属较高水平.第二个问题的解决方法是开放的，如可借助采集数据发现“身高大致是脚长的7 倍”等，并利用脚长与鞋号的一般规律进行推测，体现了数学建模活动“过程与方法”的考查，解决问题需要基于数据分析的基本方法和模型特征的学习过程，以及在建模实践中积累的经验.

例2 2017 年考古学家在郫都区古城遗址挖掘出竹木器遗存，检测发现竹木器的碳14 的残留量约为64%.一般认为死亡生物体内碳14 的残留量每隔5730年减为一半，据此估计制作竹木器的年代是（）（参考数据：lg2=0.30）.

A.公元前1421 年 B.公元前1803 年

C.公元前2460 年 D.公元前5317 年