考虑“蒸发悖论”的洱海灌区逐日参考作物蒸散发预测
2021-03-17张刘东顾世祥
赵 众,周 密,张刘东,顾世祥,2*,李 靖
(1.云南农业大学 城乡水安全与节水减排高校重点实验室,昆明 650201;2.云南省水利水电勘测设计研究院,昆明 650021;3.武汉大学 水资源与水电工程科学国家重点实验室,武汉 430072)
0 引 言
【研究意义】蒸散发(ET)作为表征太阳辐射到地面的水汽和能量转化的重要参数,是区域水循环中最重要的水文过程之一[1]。地面气象观测和卫星遥感等多途径资料分析显示,由于植被叶面积指数增加,全球自1978年以来蒸散发平均增长值为0.63 mm/a,其中植被蒸腾增加速度为0.72 mm/a,土壤蒸发则以0.32 mm/a 的速度减少[1-2]。参考作物蒸散发(ET0)又是蒸散发的气象因素分量,其估算和准确测定具有重要的现实意义[3-5]。【研究进展】逐日ET0的计算模型主要包括Penman-Monteith 公式[5]、Priestley-Taylor模型[6]、Hargreaves 公式[7]、Irmark-Allen 法[8]等方法。Penman-Monteith 公式作为联合国粮农组织(FAO)推荐的基本公式,其理论完备性、计算精度和适用性已经得到全球的公认,但所需的资料信息过多,故而在数据缺乏的地区难以使用。ET0的变化不是由于单一气象因素的变化而决定的,Traore 等[9]采用气象因素基于人工智能网络对ET0进行研究,发现Tmax是很重要的因素,但其对于预测的准确性还取决于太阳净辐射的精度和实时的天气预报信息。
除上述的理论及经验模型计算法之外,FAO 还建议使用蒸发皿资料来确定ET0(即直接法),通过设计试验环境,采用蒸发皿等观测仪器观测水面蒸发量,再经过折算系数Kp转换计算得到ET0[10-11]。蒸发皿蒸发作为揭示湖泊流域区气候变化响应最直接的指标,在我国鄱阳湖、巴丹吉林沙漠湖泊、洱海等不同地理区域的增减变化等研究均有应用[12-15]。在工程实践中过去单纯使用气温、日照等单一或多个气象因子资料,运用人工智能或统计模型的方法得到ET0估计值,近年来已逐渐将蒸发皿蒸发作为新增输入项以提高ET0估计精度[16-17]。Lennartz 等[18]将A 级蒸发皿资料用于模拟计算逐日、逐小时等不同时间尺度的ET0,发现在逐日的时间尺度下模拟值与标准值的决定系数高达0.90~0.94,但在小时等短时间尺度由于微气象环境的随机波动,模拟效果较差。也有采用辐射与温度等参数法估算ET0[19-20],效果也很好。张鑫等[21]针对西南地区分析了9 种Kp经验模型的适用性,得出A98 模型的适用性相对较好。【切入点】折算系数Kp的确定需全面考虑蒸发皿所处的下垫面、局部环境及风场和湿度等条件[5],数值范围不适于大尺度的推广使用,在计算和推广上带来一定困难。由于“蒸发悖论”现象的存在,且“蒸发悖论”的发生与时间尺度的长短又有关[22],因此在采用直接观测法对其进行分析计算时,若ET0与水面蒸发的变化趋势相反时,也会导致其结果走向出现误差。【拟解决的关键问题】探究出现“蒸发悖论”时适宜的参考作物蒸散发量估算模型。
1 材料与方法
1.1 数据资料
洱海位于云南省大理白族自治州,属澜沧江—湄公河水系,流域面积2 785 km2,年均气温15.1 ℃,年降水量1 057 mm,水资源总量10.7 亿m3[23]。全球气候变化及低纬度高原的区域响应,2010—2015年洱海地区遭遇了的连续干旱灾害,流域农业用水及农田面源加大、湖水位下降、局部区域蓝藻爆发等问题突出,洱海流域水生态保护治理已成为全国关注焦点之一[23]。使用资料包括:①洱海灌区内代表性的大理气象站1954—2018年逐日平均气温(T)、最低气温(Tmin)、最高气温(Tmax)、日照时间(n)、风速(u)、相对湿度(RH)、降水量、20 cm 蒸发皿蒸发量(Epan)。1954—2001年的20 cm 蒸发皿蒸发量为大理站实测数据,2002—2018年缺乏实测值,为保证不同年代蒸发资料的一致性,采用“云南省地表水资源”书中E601/E20=0.69 等直线图,按0.69 采用E601的实测资料对20 cm蒸发皿蒸发量进行折算。②大理、洱源、宾川等市县的自然地理、社会经济、农业综合统计年报、水利(或年鉴)等技术成果。
1.2 逐日ET0 模拟预测方法
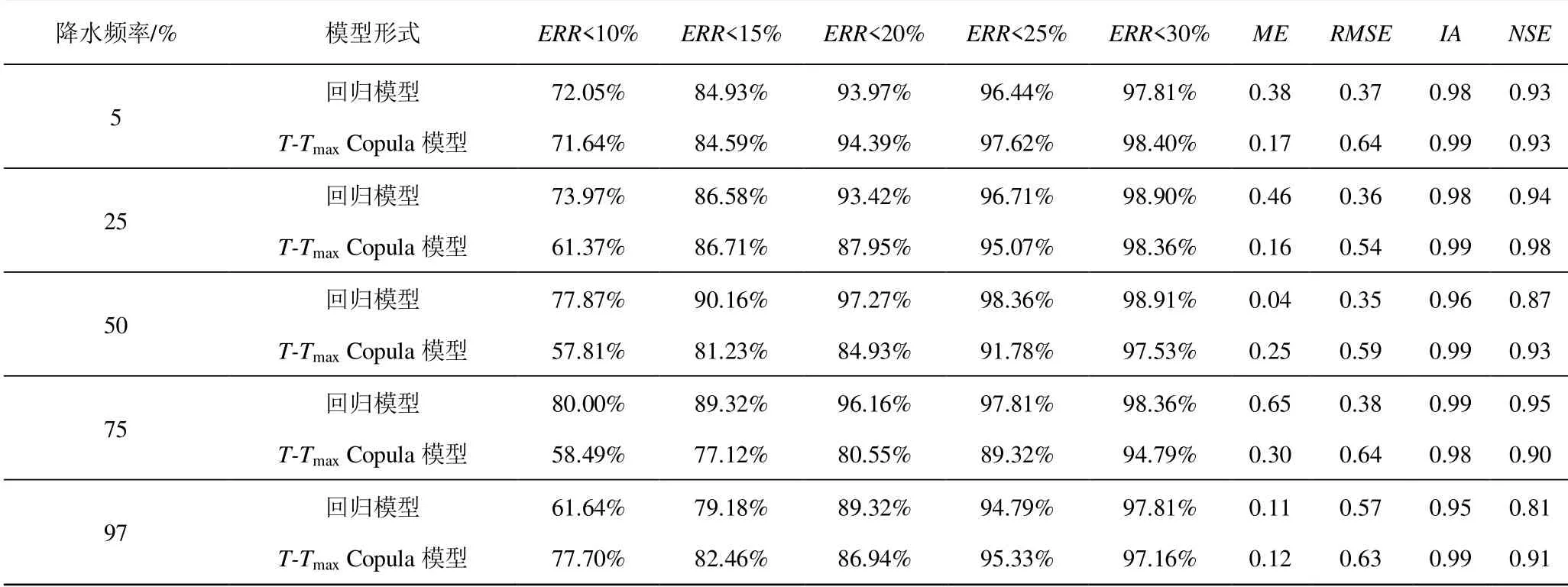
加入蒸发皿蒸发资料后,逐日参考作物蒸散发ET0预测模拟的精度得到显著提高,本质上是基于中长期蒸发皿蒸发与ET0标准值的高度相关性。但具体到不同的时期和季节,若出现“蒸发悖论”现象时,二者的变化趋势完全相反,就不能再继续使用蒸发皿蒸发来预测模拟逐日ET0了。为此,本文先采用M-K非线性趋势检验法对年、春夏秋冬季节的蒸发皿蒸发和ET0的变化进行趋势检验,识别出“蒸发悖论”时段。其次,判断模拟预测时段所处时期是否存在“蒸发悖论”现象,以决策采用不同的ET0实时预测模型方法。第三,在“蒸发悖论”时期,由于蒸发皿蒸发与ET0的变化趋势相反,只能采用随机方法之Copula联合分布函数模型预测[24]。第四,未发生“蒸发悖论”时期,蒸发皿蒸发与ET0的变化趋势一致,可采用多元线性回归模型和Kp折算系数模型,或进一步加入蒸发皿蒸发项以提高逐日ET0预测模拟的精度,其技术流程图见图1。为分析不同方法模型预报ET0的精度,使用4 个常用的统计指数来进行评估,分别为平均偏差(ME)、均方根误差(RMSE)、符合指数(IA)、Nash-Sutcliffe 效率系数(NSE)[25]。符合指数(IA)在0 和1 之间,IA越大模拟效果越好。Nash-Sutcliffe效率系数(NSE)变化范围从-∞到1,值越接近1 说明模拟值和实际值越接近。
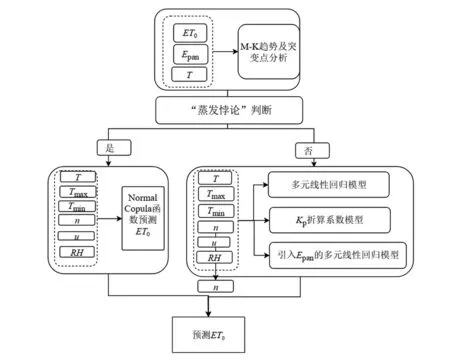
图1 技术流程Fig.1 Research technical flow chart
1.2.1 M-K 趋势检验分析
为检验ET0、蒸发皿蒸发及气温的变化趋势,采用Mann Kendall(M-K)非线性趋势检验法[26]。具体检验原理如下:
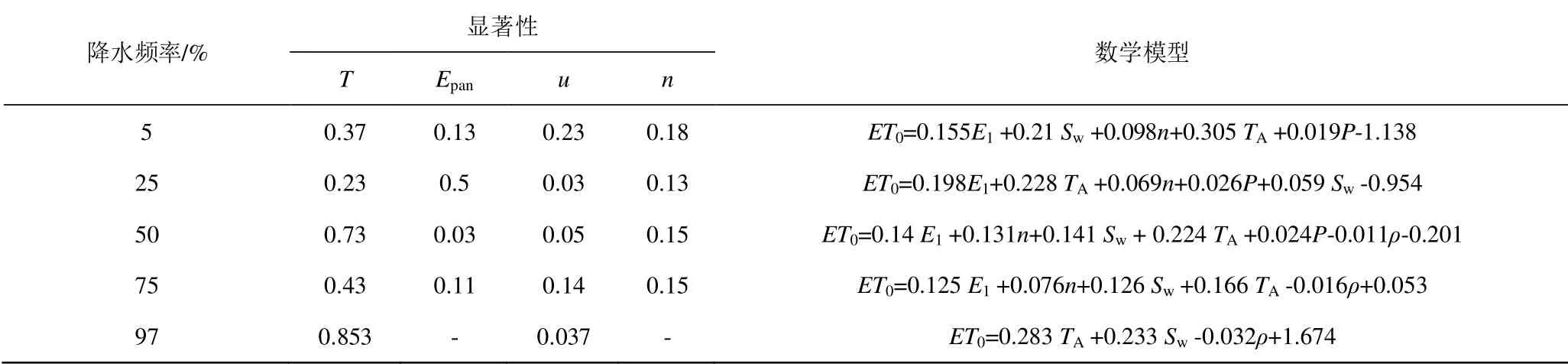
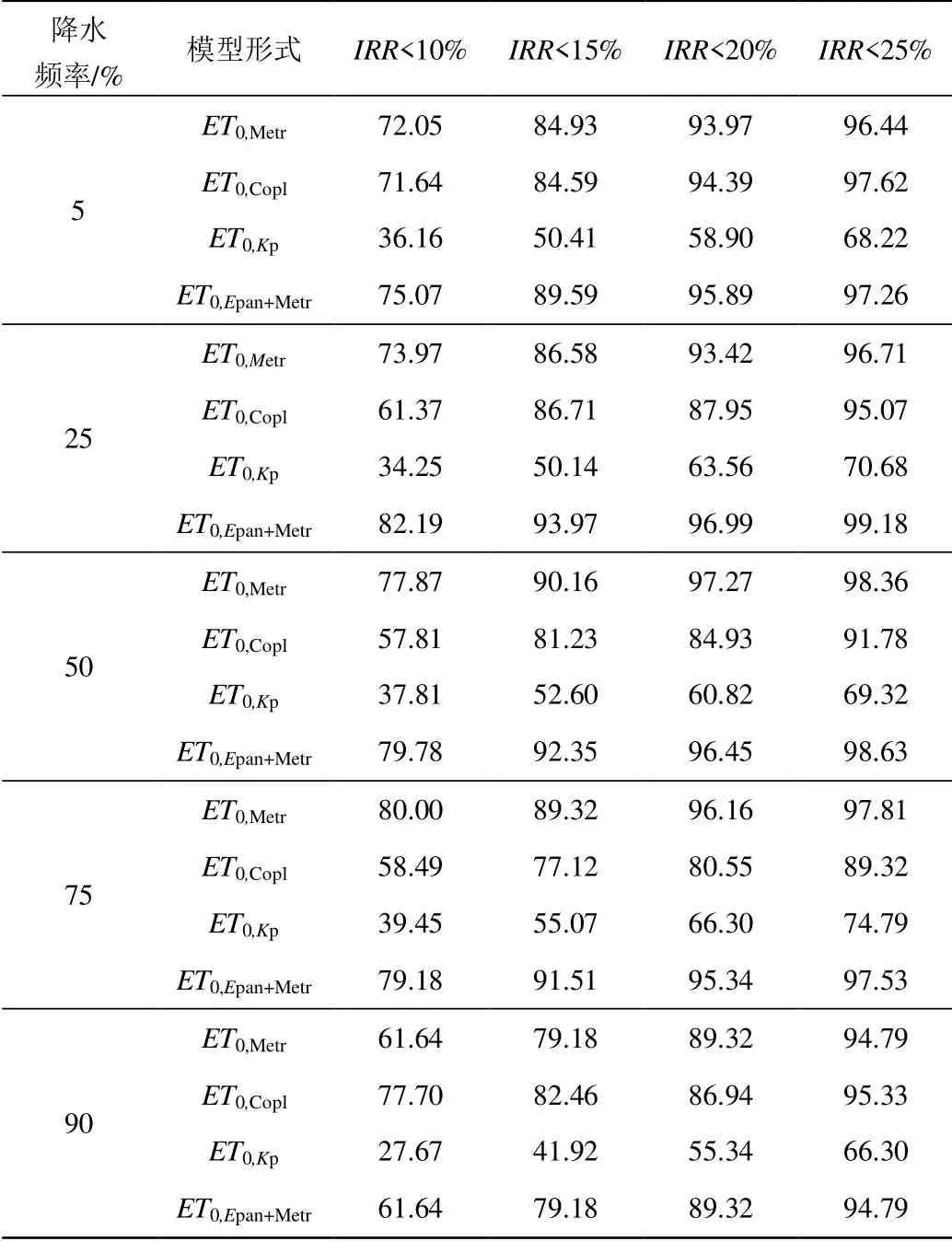
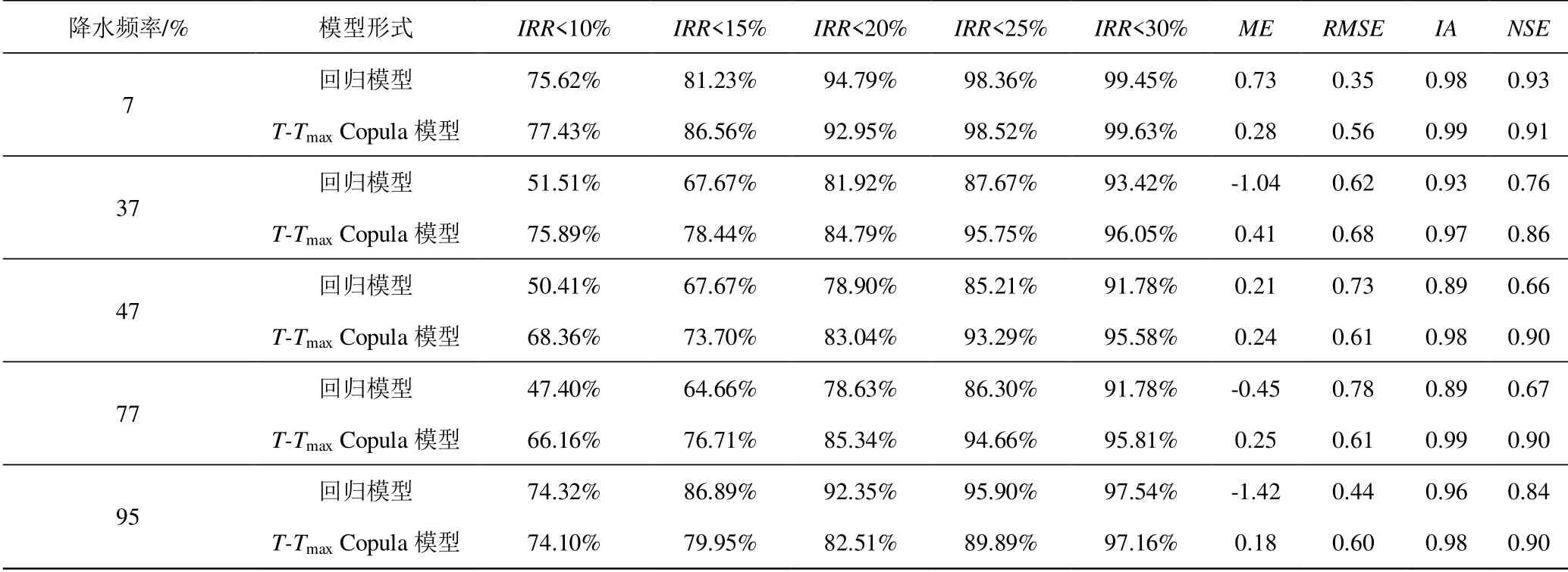
设时间序列为{xi}(i=1,2,…,n),{xj}的对偶数S(xi 式中:sgn()为符号函数;U为M-K 统计量。使用M-K 法进行突变检验时,其原理如下: 利用{xi}(i=1,2,…,n)构造一新序列,即: 式中:mi为xi>xj(1≤j≤i)的样本累积数;dk的均值以及方差定义如下: 在时间序列随机独立假设下,定义统计量: 所有的UFk组成1 条UF曲线,把同样的方法引用到反序列中,得到1 条UB曲线,将统计量UF和UB2 条曲线与±1.96 2 条直图线绘制到同一坐标表下,当出现UF和UB曲线2 条线的交点时,即为突变点。 1.2.2 多元线性回归模型 将数据输入SPSS 统计分析工具中,采用逐步回归方法进行变量引入,采用F检验概率作为判断标准值,进入概率<0.05,移除概率>0.1。 1.2.3 多元Copula 函数预测ET0 构建T、Tmax、Epan3 种气象因素的边缘分布函数,选用有代表性的正态分布、gamma 分布、lognormal分布、weibull 分布分别构建T、Tmax、Epan的边缘分布函数,并从中选择拟合效果最好的分布函数。T选择weibull 分布,Tmax选择weibull 分布,Epan选择正态分布。之后分别构建T-Tmax-Epan三维Normal Copula模型,T-Tmax、T-Epan、Tmax-Epan的3 种二维Normal Copula 模型。计算出3 种气象因素之间不同组合对应的联合分布,并将其记为预测ET0分布概率,在带回ET0的边缘分布函数中计算出ET0的值,其中ET0的边缘分布函数为gamma 函数,即为预测ET0值,优选出预测效果最佳的气象因子组合模型。详细的方法模型及应用参见相关文献[24]。 采用M-K 趋势检验法对大理站1954—2018年共65 a 的蒸散发量、气温及20 cm 蒸发皿蒸发量长时间序列变化趋势,以及各年代际间的变化趋势进行检验,结果如表1。并绘制年值及春夏秋冬季各自65 a 长时间序列的所示变化趋势线以及5 a 滑动平均曲线(图2)。 表1 大理站1954—2018年ET0、T 和Epan 的M-K 统计值Table Dali meteorological station’s M-K statistics of ET0 in 1954—2018 由表1 可知,大理站参考作物蒸散发ET0在1954—2018年长时间序列中M-K 统计值为0.07,呈上升趋势,但除1990年和2000年呈上升趋势外,其余年代呈下降趋势,由图2 可看出,整体呈上升趋势。气温的M-K 统计值为3.13,呈上升趋势,且其变化通过0.05 的显著性检验,1960、1970年及2010年呈下降趋势。由图2 可看出,整体呈先下降后上升趋势。20 cm 蒸发皿蒸发量的M-K 统计值为-5.46,呈下降趋势,且其变化通过0.05 的显著性检验,只有1990年呈上升趋势,并且并由图1 可看出,整体呈下降趋势。 春夏秋冬四季按春季2—4月、夏季5—7月、秋季8—10月、冬季11月—翌年1月分段计。对于春季,蒸散发量和气温基本上呈上升趋势,而20 cm 蒸发皿蒸发量呈下降趋势;参考作物蒸散发及气温均只有1960年和2010年呈下降趋势,20 cm 蒸发皿蒸发量在20 世纪各年代(10 a)变化不大,进入22 世纪后呈下降趋势。对于夏、秋、冬三季,蒸散发量和20 cm 蒸发皿蒸发量基本呈下降趋势,而气温大多呈上升趋势。 图2 1954—2018年ET0、气温、20 cm 蒸发皿蒸发量的变化趋势Fig.2 1954—2018 trend chart of ET0、temperature and evaporation capacity of 20 cm evaporating dish 采用M-K 趋势检验法对大理站蒸散发量、气温以及20 cm 蒸发皿蒸发量1954—2018年共65 a 的长时间序列的变化趋势以及各季节的变化趋势进行突变分析,其结果见图3。由图3 可知,蒸散发量对于全年的长时间序列来说,UF和UB的交点较多,表示其变化较为频繁,而从M-K 统计值分析可知在1960、1970年及2000年出现“蒸发悖论”,但除1960年出现交点较多外,1970年和2000年均未出现交点。对于春、秋2 季,春季突变在2008年和2016年,秋季突变在1993年和2015年。夏、冬2 季则变化较为频繁。20 cm 蒸发皿蒸发量对于全年的长时间序列来说,UF和UB的交点出现在1995年,即表示突变出现在1995年,处于1990年,但只有夏季出现“蒸发悖论”;春、冬2 季突变均出现在1996年,夏季出现在1994年,秋季出现在1987年。气温对于全年的长时间序列来说,UF和UB的交点出现在2009年,表示其突变出现在2009年,处于2000年。其春、冬2 季出现在2008年,夏季出现在2009年,秋季出现在2007年。 蒸散发量、20 cm 蒸发皿蒸发量和气温出现突变的时间不同步,这可能是由于影响蒸散发量和20 cm蒸发皿蒸发量的因素不仅有气温,还与日照、辐射、降水等多种因素有关。 图3 1954—2018年ET0、气温、20 cm 蒸发皿蒸发量的变化趋势Fig.3 1954—2018 mutation analysis of ET0、temperature and evaporation capacity of 20 cm evaporating dish 2.3.1 未出现“蒸发悖论”时期 1)单纯的气象因子多元线性回归模型法(ET0,Metr) 未引入蒸发皿蒸发项时,为方便对比计算,选择p=5%、25%、50%、75%、97%(第1 组典型年)所对应的1993、1987、1996、1986、2012年共5 a 的数据带入模型之中进行验证。构建气象因素与ET0的线性回归模型,其气象因素对ET0影响的显著性及其模型表达式见表2。表3 为不同水文年进行预测ET0,其结果与实际逐日平均ET0(作为标准值)进行对比的结果,也将Copula 联合分布函数模型法的结果一并列出(记为ET0,Copl)。由表3 可知,2 种模型的计算结果,其相对误差小于10%、15%、20%、25%的样本数比例基本上都是多元线性回归模型优于Copula 联合分布函数模型。 表2 各气象因素在不同年份对ET0 影响显著性结果(第1 组典型年)Table 2 Significant results of influence of meteorological factors on ET0 in different years(Typical year of the first group) 表3 ET0 预测值与实际值精度统计(第1 组典型年)Table 3 Statistical table of accuracy of ET0 predicted value and ET0 actual value(Typical year of the first group) 2)蒸发皿折算系数Kp模型法(ET0,Kp) 有学者研究蒸发皿系数Kp=ET0/Epan,将实际的Kp作为因变量,以实测的逐日相对湿度和2 m 高度处风速作为自变量。本文根据前人研究[21],选用A98模型,并根据大理站的气象因素将其模型修正后为下: 式中:Kp即为蒸发皿系数;U2为2 m 高度处风速;RH为相对湿度;F为生长作物顶风吹程,20 cm 蒸发皿安置与地面距离显著大于Class-A 型蒸发皿,受F影响较小,F取经验值20 m。预测结果与标准值见表4。其预测结果总体上不如采用多元线性回归模型对ET0进行预测的效果好,这可能是由于该模型在预测时间尺度较小时不适用,为进一步探究原因,又用该模型进行了月尺度的ET0预测,其结果显示,相对误差<10%的样本数增加到45%、<15%的样本数为55%、<20%的样本数为76.7%、<25%的样本数为90%、<30%的样本数为95%。由此可知,该模型在月尺度上的ET0预测精度较高,但在日尺度上预测精度较低,可能是由于大理站风速在中短时间尺度下变化各异,高原盆地和湖泊区形成的小气候影响所。 表4 Kp 蒸发皿折算系数模型ET0 预测值与实际值精度统计(第1 组典型年)Table 4 Statistical table of accuracy of ET0 predicted value and ET0 actual value of conversion coefficient model of Kp evaporating dish(Typical year of the first group) 表5 各气象因素在不同年份对ET0 影响显著性结果(引入Epan)Table 5 Significant results of influence of meteorological factors on ET0 in different years(introduce Epan) 表6 ET0 预测值与实际值精度统计(引入Epan)Table 6 Statistical table of accuracy of predicted value and actual value(introduce Epan) 3)加入Epan后的多元回归模型法(ET0,Epan+Metr) 从大理站气象因子、蒸发皿蒸发与逐日ET0的线性回归分析看,将20 cm 蒸发皿蒸发量与气象因子一并作为输入,采用多元线性规划方法推求模型参数、预测逐日ET0,并进行误差分析,结果如表5、表6所示。对比表3 未引入Epan时的结果,其预测值与实测值的精度均有提升。表7 为单纯的气象因子多元线性回归模型法(ET0,Metr)、T-Tmax二维Copula 联合分布函数模型法(ET0,Copl)、蒸发皿折算系数Kp模型法(ET0,Kp)和加入Epan后的多元回归模型法(ET0,Epan+Metr)等4 种模型方法,进行前述典型年组的逐日ET0预测,相对误差ERR小于10%、15%、20%和25%的样本量占比。由表7 可知,在未出现“蒸发悖论”的时期,加入Epan后的多元回归模型法(ET0,Epan+Metr)所得预测ET0的预测结果与标准值间的误差最小,其次为单纯的气象因子多元线性回归模型法(ET0,Metr),最差的为蒸发皿折算系数Kp模型法(ET0,Kp)。另一方面,参与对比的T-Tmax二维Copula联合分布函数模型(ET0,Copl)的预测效果总体最佳,进一步表明其方法的普适性。 2.3.2 出现“蒸发悖论”时期 为方便计算,选择p=7%、37%、47%、77%、95%(第2 组典型年,处于“蒸发悖论”期)所对应的2000、2016、2001、2003、1960年共5 a 的数据带入模型之中进行验证。构建气象因素与ET0的线性回归模型,其气象因素对ET0影响的显著性及模型见表8。由表9 可看出,在“蒸发悖论”时期,蒸发皿蒸发与同期ET0的变化趋势相反,只有采用修正后的T-Tmax二维Copula 模型(记为ET0,Copl),其预测精度也显著高于多元线性回归模型。 表7 4 种逐日ET0 预测模型的相对误差占比Table 7 Relative error ratio of four daily ET0 prediction models 表8 各气象因素在不同年份对ET0 影响显著性结果(第2 组典型年)Table 8 Significant results of influence of meteorological factors on ET0 in different years(Typical year of the second group) 表9 逐日ET0 预测值与实际值精度统计(第2 组典型年)Table 9 Statistical table of accuracy of ET0 predicted value and ET0 actual value “蒸发悖论”的结果与谢平[22]等采用云南省1981—2011年长时间序列共52 个站点的气象数据对云南省内滇西地区“蒸发悖论”的探讨结果趋势相同,“蒸发悖论”的有无与时间段的长短选取有关,长时段的研究序列可能会掩盖短时段的“蒸发悖论”现象。 蒸散发量、20 cm 蒸发皿蒸发量和气温出现突变的时间不同步,这可能是由于影响蒸散发量和20 cm蒸发皿蒸发量的因素不仅有气温,还与日照、辐射、降雨等多种因素有关[27]。孙洁等[28]通过对鄂尔多斯的蒸散发研究,发现风速的下降是潜在蒸散发量减小的主要因素;同时,日照时间的减小和降水量的增加也是鄂尔多斯高原西部潜在蒸散发量减小的关键因素。与分析结果相一致。 对于参考作物蒸散发量ET0的多元线性回归模型预测方法、数值计算方法都有较多研究[5-11],本文将“蒸发悖论”与几种计算方法相结合,找出在未出现“蒸发悖论”时采用线性回归模型方法较优,而在出现“蒸发悖论”时,则采用高维Normal Copula 函数模型进行预测较优。 在1954—2018年的长时间序列上,洱海流域大理站的20 cm 蒸发皿蒸发量均呈下降趋势,参考作物蒸散发量ET0和气温呈上升趋势,ET0的上升趋势更平缓,但在短时间序列上结果存在年代各异性。 未出现“蒸发悖论”时期,加入Epan后的多元回归模型法(ET0,Epan+Metr)所得逐日ET0的预测结果与标准值间的误差最小,其次为单纯的气象因子多元线性回归模型法(ET0,Metr),最差为蒸发皿折算系数Kp模型法(ET0,Kp)。因此,可采用加入Epan后的多元回归模型法(ET0,Epan+Metr)进行逐日ET0预测,气温对其影响的显著性最大。出现在“蒸发悖论”时期,采用T-Tmax二维Normal Copula 模型的精度更高。 采用加入Epan的多气象因子线性回归模型进行预测时,其预测结果精度较高。而采用二维Normal Copula 模型预测所需气象因素却是最少,可在气象因素缺失时获得较好的预测结果。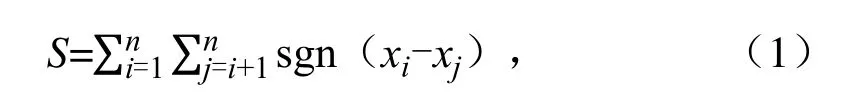




2 结果与分析
2.1 变化趋势分析
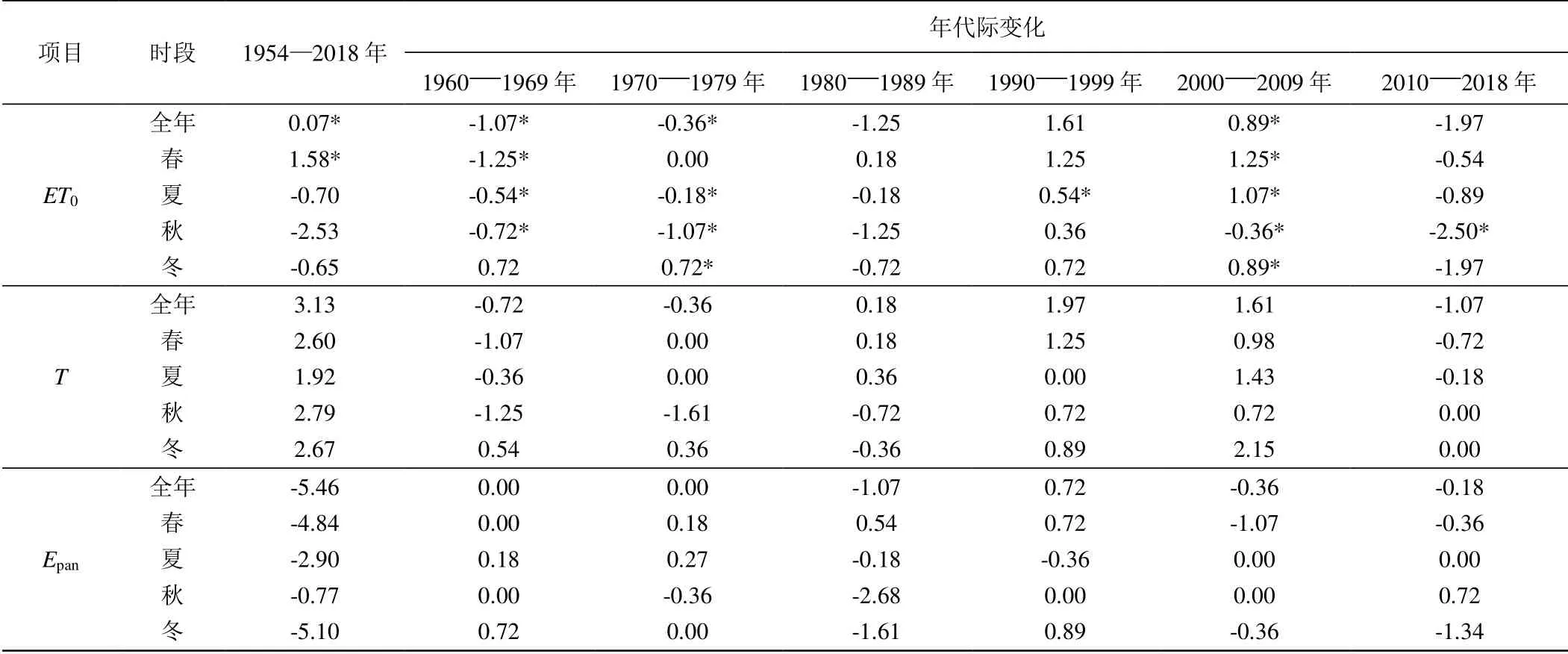

2.2 突变分析
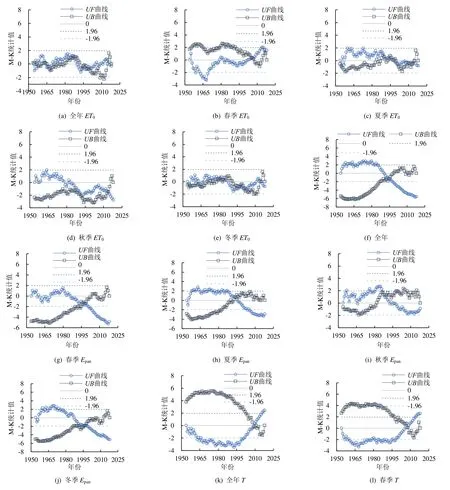

2.3 逐日ET0 预测方法对比分析

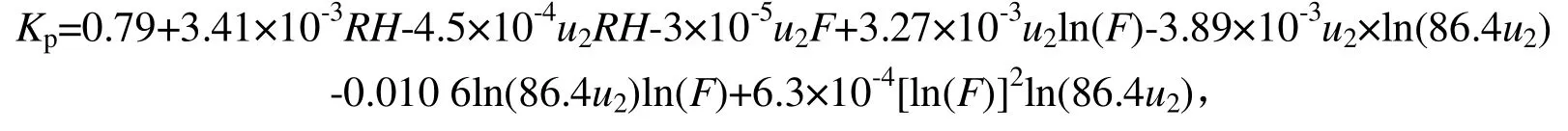



3 讨 论
4 结 论
