基于改进灰狼算法的天线设计优化

2021-03-17姚钦海项铁铭

杭州电子科技大学学报(自然科学版) 2021年1期

姚钦海，项铁铭，孙斌

(杭州电子科技大学电子信息学院，浙江杭州 310018)

0 引言

伴随着高速发展的无线技术和通信技术，多输入输出技术(Multiple Input and Multiple Output， MIMO)极大地提高了信道容量，改良了通信质量。但MIMO天线的隔离度过高，将导致天线性能下降，所以，如何改善天线的隔离度及其性能成为一个值得研究的方向。

2014年Mirjalili等基于灰狼捕食行为提出了的灰狼优化算法(Grey Wolf Optimizer，GWO)[1]。GWO算法具有原理简单、参数少等特点，可应用于诸多工程领域。例如，Guha等[2]将对立学习应用到灰狼优化算法中，解决了负载频率控制的问题，并进一步提高了负载频率控制的性能； 2018年Zhou等[3]通过差分进化算法，进一步生成了更适合灰狼优化算法的初始种群，并改进了灰狼算法应用于优化支持向量机的色差分类。本文对标准灰狼优化算法进行改进，通过测试函数验证其性能，并应用于MIMO天线优化设计中，进一步证明了算法的可靠性，为天线优化设计提供新思路。

1 基础理论

1.1 标准灰狼优化算法

GWO中主要分为α，β，δ和ω等4个等级制度，灰狼在捕猎过程中，其它狼在头狼α的带领下通过逐步缩小包围圈的形式攻击猎物。其数学模型如下：

D=|CXP(t)-X(t)|

(1)

X(t+1)=XP(t)-AD

(2)

式中，t为当前的迭代次数，X(t)为当前灰狼第t次迭代时所处的位置，XP(t)为猎物的位置，系数A和C从下面公式中得到：

A=2ar1-a

(3)

C=2r2

(4)

式中，r1和r2为[0,1]之间的随机数，a从2到0线性减小。

在狩猎过程中保存了α，β，δ的位置作为当前所获得的前3个最佳解决方案，并要求其它搜索代理根据最佳搜索代理的位置来更新其位置，因此给出：

Dα=|C1Xα(t)-X(t)|

(5)

Dβ=|C2Xβ(t)-X(t)|

(6)

Dδ=|C3Xδ(t)-X(t)|

(7)

X1=Xα-A1Dα

(8)

X2=Xβ-A2Dβ

(9)

X3=Xδ-A3Dδ

(10)

(11)

式中，X1,X2,X3分别为α，β，δ狼的位置，X(t+1)为当前狼的位置。

1.2 可用于WLAN的紧凑型双频MIMO

文献[4]介绍了一款能覆盖WLAN的紧凑型MIMO天线，其结构如图1所示。该天线工作介质基板采用FR4材料，厚度为0.8 mm，长宽分别为L和W，采用微带线馈电，天线中间有2条长宽分别为L1和L2的地板枝节和长宽分别为L4和L3的地板缝隙，2条地板枝节之间的距离为L5，位于两侧的是F型天线，其两臂的长分别为P1和P2，宽为P。

图1 天线模型结构图[4]

2 改进灰狼优化算法

2.1 基于拟蒙特卡罗方法的种群初始化

标准灰狼算法采用随机初始化方法对种群进行初始化，这就导致初始种群分布不均匀。本文拟采用蒙特卡罗方法(Monte Carlo method)中的Hammersley序列解决该问题，利用Hammersley序列的均匀分布初始化种群。其中序列生成步骤如下所示[5]。

(1)用素数p来表示任一自然数n，如：

(12)

式中，ai∈[0,p-1]。

(2)将上述表达式的系数am,a1,a0反序排列，并在前面加上小数点，求其值可得：

φp(n)=(0.a0a1…am)p=a0p-1+a1p-2+…+amp-m-1

(13)

(3)n的维度为d，则d维空间的Hammersley均匀序列值：

(14)

将搜索空间一分为二之后，使用式(14)在每个子空间中生成，事先设定好的N个种群序列点集H，进一步通过映射规则将点集H其分散在子空间内，映射规则如下所示：

S(i,∶)=L+(M-L).*H(i.∶)

(15)

S(i+j,∶)=M+(U-M).*H(i.∶)

(16)

式(15)和(16)中，L和U分别表示搜索空间的上下边界，M表示搜索空间一分为二后的中间边界，“.*”表示乘法运算，i和j分别表示一分为二后的两个子空间的相关维度。按照适应度值排序，初始化种群为前N个种群。

2.2 基于纵横交叉的相关策略

纵横交叉算法主要包含横向、纵向交叉操作及竞争操作[6]。横向交叉操作主要是对父代个体xi和xj的第d维进行横向交叉操作，表示如下：

(17)

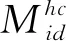
纵向交叉算子是针对同一个体在不同维度之间的纵向交叉操作。对个体i的第d1和d2维进行纵向交叉操作，表示如下：

(18)

2.3 改进非线性收敛因子

标准灰狼优化算法中存在随机参数A和C，在算法的勘探能力研究中，参数A和C至关重要。当参数|A|>1时，代表算法正进行全局勘探；当参数|A|≤1时，代表算法正进行局部勘探。根据(3)，参数A的变化主要取决于收敛因子a，随着迭代次数的增加a线性递减。考虑到线性递减并不能很好地说明实际收敛的寻优过程，因此这里提出了一种改进型的收敛因子非线性函数：

(19)

式中，aMax和aMin的值一般取2和0，t和T分别表示当前和最大迭代次数，调节系数m是大于0的正整数，经过多次实验后得到当m为14时，算法的总体寻优性能最佳。

3 实例设计与分析

为了验证本文改进算法的性能，本文设计了一款双频MIMO天线，通过仿真测试来说明算法的可行性。用于WLAN的紧凑型双频MIMO天线设计要求为：尽量降低天线在工作频段内的回波损耗，控制所有工作频段隔离度的上限为-15 dB。因此，将目标函数设置为：

(20)

(21)

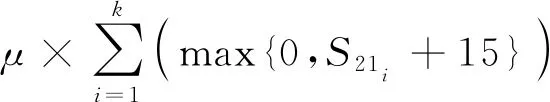
本文选用4个测试函数，如表1所示。选取标准GWO算法和本文改进的灰狼优化算法(CSGWO)及现有改进良好的3种灰狼优化算法——魏政磊等[7]提出的SAGWO算法、王梦娜等[8]提出的SMIGWO算法、马俊等[9]提出的MGWO算法进行性能测试。5种算法采用相同设置：维度为10，种群数30，迭代次数1 000次，并进行30次独立运行。

表1 测试函数

5种算法测试结果如表2所示，从平均值看，CSWGO算法在4个测试函数中都优于其它算法，其中在f2和f4函数中能够收敛到最优解，说明CSGWO有较好的收敛性能；从标准差看，CSGWO算法在f2，f3，f4中优于其他算法，说明CSGWO算法有较好的鲁棒性。为了直观地反映CSGWO算法的收敛性能和趋势，得到CSGWO，MGWO，GWO算法的收敛图如图2所示，从图(a)，(c)，(d)中的收敛曲线可以看出，CSGWO算法的收敛精度和收敛速度都要要比其它2种算法更优，图(b)中，虽然CSGWO和MGWO算法都能够收敛到最优解，但是很显然CSGWO算法的收敛速度更快。