四蹄分体式制动器的制动效能分析

平思亮，苏铁熊，杨世文，魏 星

(1.中北大学能源动力工程学院，山西 太原 030051)(2.山西省星羽制动器有限公司，山西 太原 030051)

目前市场上的鼓式制动器各式各样，其中领从蹄鼓式制动器制动效能及稳定性皆处于中游水平[1-2]，但存在领、从蹄单位压力不相同而导致的摩擦衬片磨损不均匀、寿命低的缺点[3]。双向双领蹄式制动器的蹄片都是领蹄，因而具有较高的制动效能[4]，但其制动器有两个轮缸，结构复杂且间隙调整困难。双向增力式制动器[5]内部制动蹄片上端由两个活塞驱动，下端由推杆连接，因两蹄片均为领蹄，所以制动器效能稳定性比较差。此外，双从蹄鼓式制动器[6]的制动效能稳定性最好，但因制动器效能最低所以很少使用。2018年徐军[7]提出电控自增力鼓式制动器，通过一套电控机械装置调整领蹄的支承点来提高制动器的制动效能，以补偿由于摩擦材料的热衰退而引起的摩擦系数降低的问题，存在系统复杂、成本高、维修困难等问题。通过分析以上各鼓式制动器的优缺点，本文设计了一种新型四蹄分体式制动器，其优点是具有4个制动蹄，增大了摩擦衬片总体的包角，使制动器散热性能更好，摩擦衬片磨损相对均匀，制动器效能以及效能稳定性更好，缺点是结构略微复杂。

1 四蹄分体式制动器结构

四蹄分体式制动器的结构如图1所示，其为轴对称结构，单侧由领蹄、从蹄以及间隙调整机构组成。通过两个非平衡式制动凸轮上下驱动，为制动蹄提供张开力。粘接有摩擦衬片的4个制动蹄片均匀分布在制动鼓内侧，摩擦衬片起始角为零，实现了摩擦衬片接触面积的最大化，有效提高了制动效能。

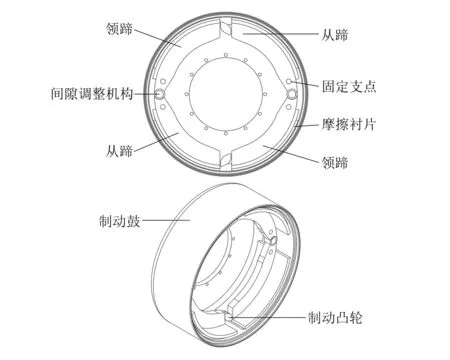
图1 四蹄分体式制动器结构

2 四蹄分体式制动效能数学模型

与传统的领从蹄鼓式制动器数学模型相比，四蹄分体式制动器具有4个制动蹄，摩擦衬片起始角为零，包角大，驱动机构多。本文建立了四蹄分体式制动器制动蹄片的制动力矩、摩擦力、摩擦力作用半径的数学模型。

2.1 制动力矩数学模型

与传统的领从蹄鼓式制动器相同，四蹄分体式制动器每个蹄有1个自由度，以领蹄为分析对象，产生的制动力矩Tμ1为:

Tμ1=fF1ρ1

(1)

式中:f为摩擦系数；F1为领蹄的法向合力；ρ1为摩擦力fF1的作用半径，如图2所示。

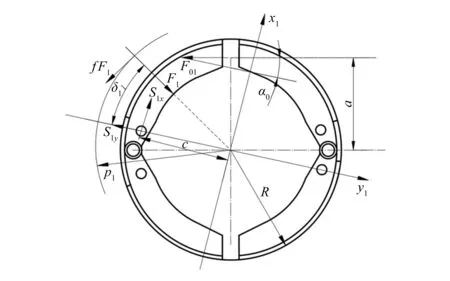
图2 张开力计算简图

2.2 摩擦力数学模型

为计算张开力F01与F1的关系，对鼓的中心点取矩，列平衡方程式得:

-F01sinα0+S1x-F1(sinδ1+fcosδ1)=0

F01a-S1xc+fF1ρ1=0

(2)

式中：δ1为y1轴与F1的作用线的夹角；S1x为固定支点对领蹄的支撑反力在x1轴的分力；α0为张开力F01与y1轴的夹角；a为张开力F01到制动鼓中心的距离；c为固定支点到制动鼓中心的距离，如图2所示。

由式(2)得到法向合力F1为:

(3)

则领蹄的摩擦力Ff1为：

(4)

同理可得从蹄的摩擦力Ff2为：

(5)

式中：F2为从蹄的法向合力；ρ2为摩擦力fF2的作用半径；δ2为y1轴与从蹄的法向合力F2的作用线的夹角。

2.3 作用半径及法向合力与y1轴的夹角数学模型

四蹄分体式制动器的制动蹄受力不均匀，与领从蹄鼓式制动器一样，制动蹄上压力同样遵循沿摩擦衬片长度方向的正弦分布规律，即：

p1=pmaxsinα

(6)

式中：p1为领蹄表面上某一点的压力；pmax为领蹄表面的最大压力；α为任意作用力与y1轴之间的夹角。

在摩擦衬片表面取一横向微元面积，如图3所示，微元面积为bRdα，其中b为衬片宽度，R为制动鼓半径，dα为包角。

图3 制动力矩的计算简图

摩擦力fdF1产生的制动力矩dTμ1为：

dTμ1=fdF1R=fpmaxbR2sinαdα

(7)

再由y1轴与摩擦衬片起始端夹角α到y1轴与摩擦衬片起终端夹角α″区段对式(7)积分，得：

Tμ1=pmaxbR2f(cosα′-cosα″)

(8)

y1轴与法向合力F1存在一个夹角δ1，利用微元法求解δ1，把dF1看作投影在x1轴和y1轴上分量dF1x和dF1y的合力，则F1为:

(9)

其中：

(10)

(11)

式中：β=α″-α′，为摩擦衬片包角。

由此推导可得夹角δ1:

(12)

联合式(1)、(8)、(9)求得摩擦力的作用半径ρ1为：

(13)

同理，在结构尺寸相同的情况下，可求得从蹄的法向合力F2与y1轴的夹角δ2及作用半径ρ2。

2.4 制动效能因数的数学模型

制动效能因数Kt是在制动鼓作用半径ρ1上的摩擦力(Tμ/ρ1)与输入力(张开力F01)之比：

(14)

故领蹄制动效能因数Kt1为：

(15)

同理，从蹄制动效能因数Kt2为：

(16)

由于四蹄分体式制动器有4个蹄片，故总制动效能因数Kt为：Kt=2Kt1+2Kt2。

3 基本参数的确定与计算结果分析

3.1 结构设计参数

该四蹄分体式制动器的主要设计参数见表1。

表1 四蹄分体式制动器设计参数

3.2 计算结果

由四蹄分体式制动器的主要设计参数计算可得：作用半径ρ1=ρ2=221 mm；法向合力与y1轴的夹角δ1=δ2=37.566°。

四蹄分体式制动器的领蹄制动效能因数之和为2Kt1=1.116；从蹄制动效能因数之和为2Kt2=0.711；制动器总制动效能因数Kt=1.827。

3.3 四蹄分体式与领从蹄式制动器效能因数对比

图4为领从蹄鼓式制动器结构示意图，其基本参数见表2，结合制动效能的数学模型可以获得领从蹄鼓式制动器制动效能因数。

制动效能因数随摩擦系数变化趋势如图5和图6所示。由图5可以看出，f<0.35时，四蹄分体式制动器领蹄-从蹄制动效能优于领从蹄鼓式制动器领蹄；0.35≤f≤0.45时，制动效能降低；0.10≤f≤0.45时，四蹄分体式制动器领蹄-从蹄制动效能明显优于领从蹄鼓式制动器从蹄。制动器的摩擦系数f=0.35时最接近理想状态，因此0.35为最佳摩擦系数，此时四蹄分体式制动器领蹄-从蹄布局既能保持领从蹄鼓式制动器领蹄的制动效能，又能提高领从蹄鼓式制动器从蹄的制动效能，从而改变了传统领从蹄鼓式制动器两侧制动效果相差大的现象，解决了领蹄比从蹄磨损严重的问题。

图4 领从蹄鼓式制动器示意图

表2 领从蹄鼓式制动器基本参数

图5 制动器单侧效能因数对比图

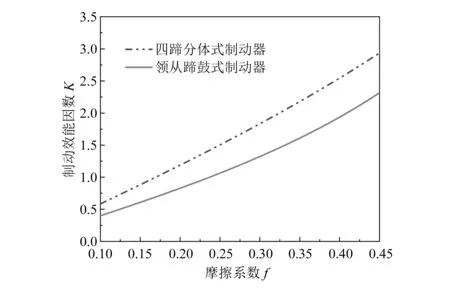
图6 四蹄分体式与领从蹄鼓式制动器的总制动效能对比图

图6中，0.10≤f≤0.45时，四蹄分体式制动器的制动效果一直优于传统的领从蹄鼓式制动器。在f=0.10时，四蹄分体式制动器的制动效能因数是0.584，相较于领从蹄鼓式制动器的制动效能因数0.399提高了46.37%；在最佳状态f=0.35时，四蹄分体式制动器的制动效能因数是2.236，相较于领从蹄鼓式制动器的制动效能因数1.603提升了39.49%。总体上，四蹄分体式制动器制动效果更佳。

4 结束语

本文在已有的传统领从蹄鼓式制动器基础上建立了四蹄分体式制动器的数学模型。研究结果表明，四蹄分体式制动器能够改善领从蹄鼓式制动器中领蹄制动效果优于从蹄的现象，中和两侧制动效果不均衡的问题，避免领蹄比从蹄磨损严重的现象。虽然新型四蹄分体式制动器结构略显复杂，但在最佳摩擦系数0.35时，四蹄分体式制动器制动效能因数相较于传统的领从蹄鼓式制动器提升了39.49%，制动效果更优，为下一步的制动器应用研究提供了理论依据。