基于机器学习的压裂优化研究
2021-03-16崔博宇董易凡杨圣方刘博卿
崔博宇,董易凡,杨圣方,刘博卿
中国石油长庆油田苏里格南作业分公司(陕西 西安 710018)
0 引言
水力压裂优化是一项包含岩石力学、流体力学、工程学和数据科学等多方面学科的复杂课题[1]。鉴于苏里格南的大规模、工厂化作业模式产生了超过1 300 个层位的优质压裂数据。其大数据量的特点不仅为机器学习提供了“原材料”,而且变量少的特点又减轻了机器学习的工作量,因此理论上存在基于机器学习进行压裂优化的可能性。数据预处理和建模分析等机器学习均是应用Python 语言[2]完成。
基于机器学习的压裂优化设计思路:将压后产量假设作为储层储能和压裂作业两项自变量相互作用的因变量表现。通过机器学习分析这三项历史数据,建立数据模型[3],从而在一定条件下通过优化压裂施工参数,增加提高压后产能的可能性。
1 数据预处理
本次研究的数据预处理包括从收集的1 347 个层位数据中去除了不具有代表性、数据量过少的层位(盒7 和山2)和压裂方式(水平井压裂和Hi-Way压裂)。处理后的1 219 个层位数据包括659 个盒8层位和560个山1层位的井丛井压裂。
1.1 储层数据信息
1.1.1 垂深对比
通过数据分析及综合比较发现盒8层位的储层深度要比山1 层位浅。其中盒8 层位的垂深主要集中在(3 500±70)m。山1 层位的垂深主要集中在(3 570±70)m。
1.1.2 孔隙度
综合比较盒8 层位和山1 层位的孔隙度,数值近似相等,且分布集中。盒8 层位的孔隙度主要集中在7.0%±1.6%。山1 层位的孔隙度主要集中在6.7%±1.4%。
在东莞石排镇产业现有资源的基础上,建立东莞石排镇各类企业之间的密切联系,形成企业的核心价值。并在政府宏观调控的政策下构建核心服务体系,形成区域较高的核心能力。并构建完善的培育机制,构建石排镇强大的核心团队。
1.1.3 渗透率
综合比较盒8 层位和山1 层位的渗透率数值近似相等,且分布集中。盒8 层位的渗透率主要集中在(0.109±0.06)×10-3μm2。山 1 层位的渗透率主要集中在(0.105± 0.04)×10-3μm2。
1.1.4 砂体厚度
综合比较知,盒8 层位要比山1 层位的砂体厚度厚。盒8层位的砂体厚度主要集中在6.5~15.3 m。山1层位的砂体厚度主要集中在5.3~13.0 m。
1.2 压裂数据信息
1 219 个层位包括 659 个盒 8 层位和 560 个山 1层位的压裂数据,其用支撑剂设计体积、支撑剂施工体积、压裂液设计体积、压裂液施工体积、前置液设计体积、前置液施工体积6 个重点变量描述压裂信息。通过数据可视化后,发现支撑剂体积和压裂液体积呈现近似线性关系,如图1(a)所示;如图1(b)所示,支撑剂体积和前置液体积呈现近似线性关系。山1和盒8层位均呈类似规律。
1.3 产量数据信息
产量数据通常包含投产前的无阻流量(AOF)和投产后一段时间内的累计产量。由于一口井可能存在多个层位,一口井的压后产量无法简单地和每一层的储层和压裂数据建立变量联系,因此产量数据的选择难度非常大。但单层位井,每口井只有一层,则压后产量和储层与压裂数据建立的联系是准确的。
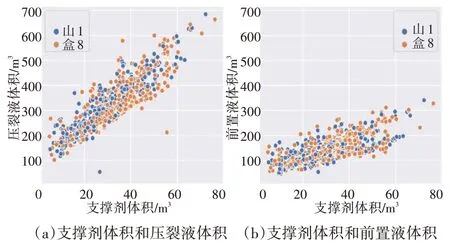
图1 压裂信息层位对比
在选择机器学习输入产量数据上,鉴于准确性和实验性考虑,选择投产前158 口单井单层的无阻流量作为最终输入数据。盒8层位的动态无阻流量数值平均值介于(5~22)×104m3/d。山1 层位的动态无阻流量数值平均值介于(5~21)×104m3/d。盒8 层位的无阻产量平均值要高于山1层位的产量平均值(表1)。
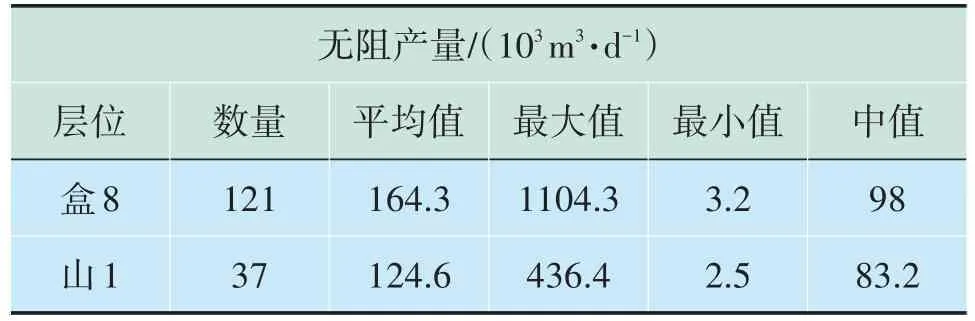
表1 苏里格南层位无阻产量信息
2 机器学习模型
2.1 模型变量的选择
模型变量的选择处理。从收集的1 219 个层位压裂数据中,通过数据特征排序得出,在以压后产量无阻流量为因变量的条件下,经过机器学习中的变量排序,以信息增益率为指标[5],支撑剂体积和砂体厚度分别以0.05 和0.046 的得分排在前两位,因此选用该两项变量作为模型应用的自变量。从而将原始数据尽可能简化成易分析、可解读的三维数据。通过数据预处理,最终确定建立压裂优化模型的变量组合:自变量X为砂体厚度,单位m;支撑剂体积Y,单位m3;因变量压后产量Z,单位103m3/d。
2.2 模型的算法
数据模型的算法:首先应用降维算法将预处理得到的3 维数组降维成2 维,分析出2 维数据关系后,再将数据升维成3维数组,最后利用回归算法得到的3维数组方程进行变量优化。
其中降维和升维的工作均在Python 中运用模型参数主向量PCA/主成分分析实现[6]。降维后的2维数组通过数据可视化分析发现,PCA和AOF的关系呈开口向下的抛物线关系,即在一定条件下,PCA的取值有最大值。当PCA取最大值时,对应的砂体厚度和支撑剂体积即为压裂优化的优选参数。为了获得PCA的最优值,利用无阻流量将2 维数据升维成新的3维数据。
升维后的3 维数据应用线性回归求解后,得到线性回归方程式:
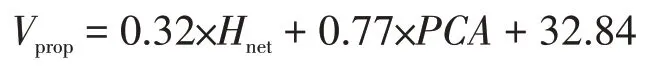
式中:Vprop为支撑剂体积,m3;Hnet为砂体厚度,m;PCA为模型参数主向量。
3 机器学习模型结果解释
最终求解出的回归方程,即为压裂优化方程。结合图2 的主向量与无阻流量选择曲线图,可以画出优化曲线,其含义是在已有数据训练的模型下,模拟结果解释为在储层厚度一定的情况下,支撑剂体积和压后产能表现呈现开口向下的抛物线关系,即当支撑剂体积在设计条件允许的情况下,尽可能地靠近顶点,可以增加提高产能的可能性。过少的支撑剂体积可能不利于压后产量表现,而过多的支撑剂体积则可能不会增加压后产量表现。
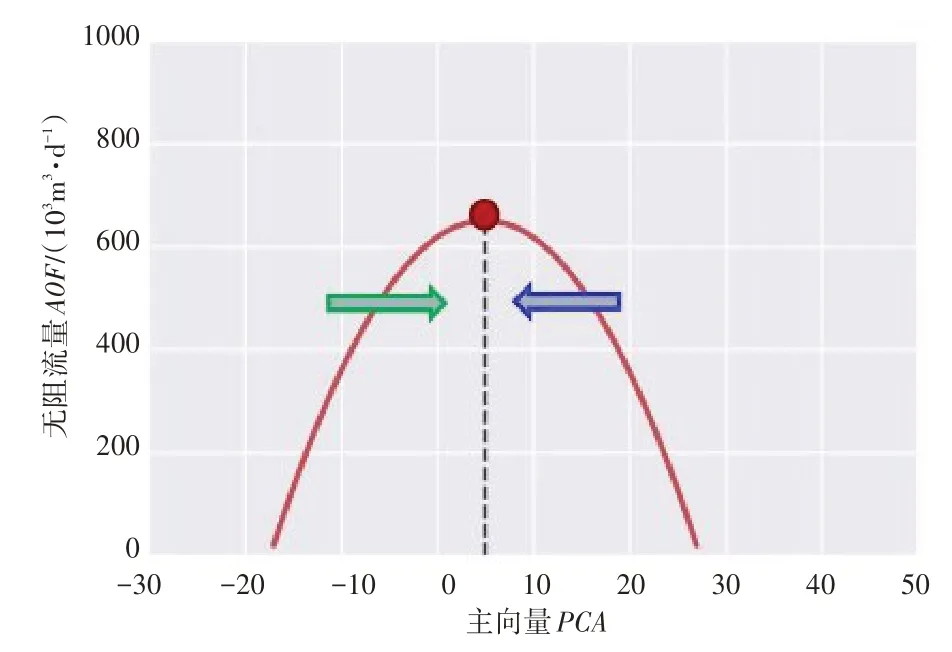
图2 主向量与无阻流量选择曲线图
图3 为砂体厚度和支撑剂体积的优化曲线图。结合回归公式可知,当PCA= 5 时,抛物线达到顶点,此时的最优支撑剂体积与砂体厚度的关系(图3中红色实线)为:Vprop=0.32×Hnet+36.69。
当PCA= -5 时,其位于抛物线顶点的左侧,此时的支撑剂体积与砂体厚度的关系(图3 中绿色虚线)为:Vprop=0.32×Hnet+28.99。
当PCA=15 时,其位于抛物线顶点的右侧,此时的支撑剂体积与砂体厚度的关系(图3中蓝色虚线)为:
Vprop=0.32×Hnet+44.39
在压裂施工中,如果在压裂设计条件允许的情况下,结合砂体厚度,可以适当调整砂量。当设计的砂量使PCA落在顶点左侧时,可以适当加大砂量,以达到获得最优PCA的目的;当设计的砂量使PCA落在顶点右侧时,可以适当减小砂量,以达到获得最优PCA的目的。
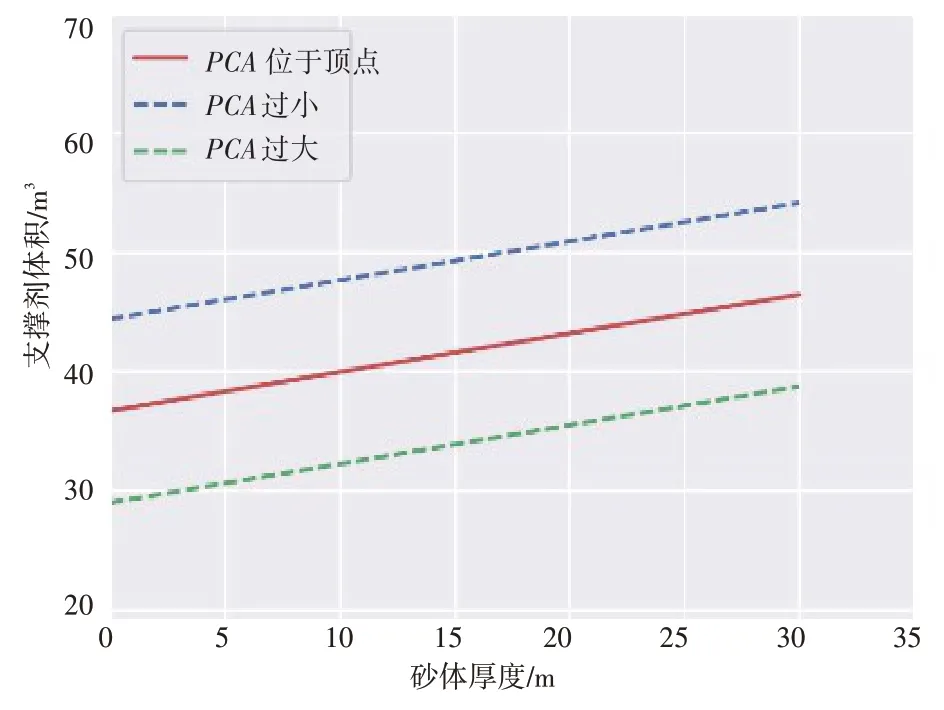
图3 压裂参数优化图
考虑到实际情况下的最优值会和理论最优值有差距,但是从优化的角度,提供若干个支撑剂体积设计参数后,结合砂体厚度,通过与对应的PCA理论值比较,可以提供设计支撑剂体积使PCA处于上升通道(抛物线顶点左侧)还是下降通道(抛物线顶点右侧)。因此优化的空间即为让设计值落在蓝色虚线和绿色虚线之间,并尽可能地靠近红线,即为模型给出的最优设计。
4 模型应用实例
以砂体厚度10 m 为例说明压裂优化模型的意义,如图4所示。结合线性方程可知,砂体厚度由模型给出的加砂量为40 m3时,PCA=5达到最优。
当砂量为32 m3时,对应的PCA值为-5,结合砂体厚度和压裂设计等因素后,应适当增加支撑剂体积。
当砂量为48 m3时,对应的PCA值为15,结合砂体厚度和压裂设计等因素后,应适当减少支撑剂体积。
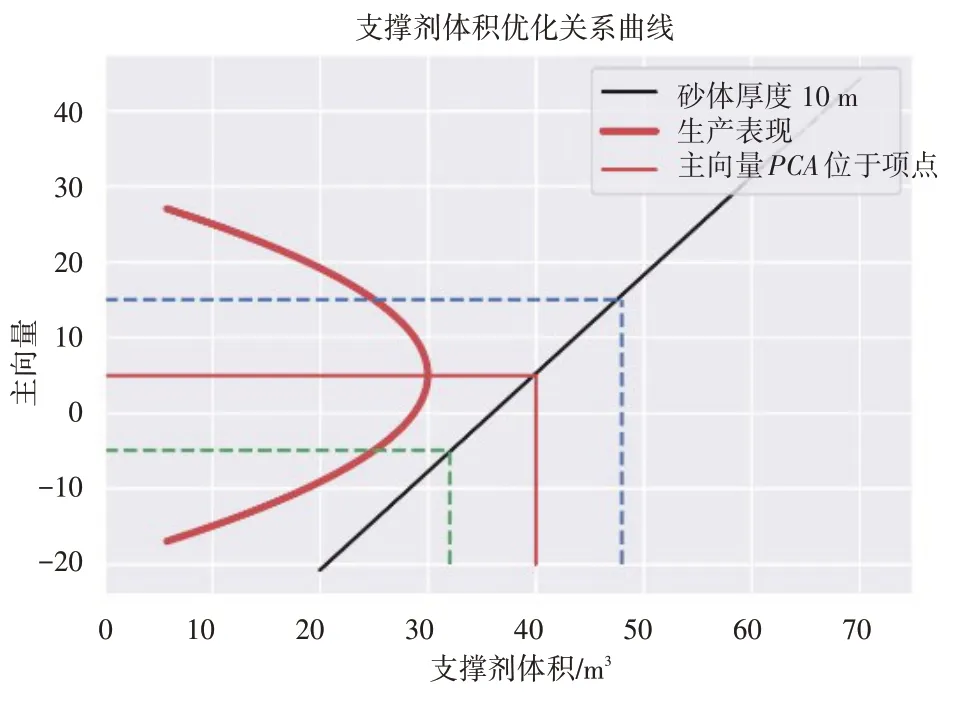
图4 机器学习模型应用示意图
5 结论与建议
在假设压后产量是砂体厚度和支撑剂体积两项自变量相互作用的因变量表现的条件下,应用机器学习算法可以实现压裂设计优化方案。
1)在储层厚度一定的情况下,支撑剂体积和压后产能表现呈开口向下的抛物线关系。
2)当设计支撑剂体积在模型给出的最优值左侧时,设计条件允许的情况下,增加支撑剂体积,可以增加提高产能的可能性。
3)当设计支撑剂体积在模型给出的最优值右侧时,代表过多的支撑剂体积可能不会增加压后产量表现,应适当减少设计支撑剂体积。
4)机器学习模型是以158口单井单层的投产前无阻流量作为因变量,模型在投产后累计产量为因变量的情况仍需继续研究。
5)机器学习的压裂参数优化是建立在单一模型的基础上,其他算法下的机器学习模型仍需继续研究,以作为最终的优化模型投入实际生产。
