精准构建物理模型 提升复习备考效率

>>>邢莉娟 朱增龙

经过系统全面的一轮复习， 考生对物理学的基本概念、规律、方法、技能及其应用进行了重新熟悉，薄弱环节得以加强，章节结构、知识网络初步得以梳理，接下来的二轮复习必将进一步加强知识的网络化、 系统化，突出横向联系、纵向挖掘。 想要在有限的时间内提高复习效率， 必须掌握构建物理模型的方法，它可以将知识穿成串、织成网，提升考生解决一类问题的能力。

一、试题分析

2020 年山东卷的物理试题情景新颖，与实际联系紧密，对考生的物理思维要求很高。 下面以该卷16 题为例， 谈谈对物理斜抛运动模型的构建。

（2020 年山东卷16 题）单板滑雪U 型池比赛是冬奥会比赛项目，其场地可以简化为如图甲所示的模型： U 形滑道由两个半径相同的四分之一圆柱面轨道和一个中央的平面直轨道连接而成，轨道倾角为17.2°。 某次练习过程中，运动员以vM=10 m/s 的速度从轨道边缘上的M 点沿轨道的竖直切面ABCD 滑出轨道，速度方向与轨道边缘线AD 的夹角α=72.8°，腾空后沿轨道边缘的N 点进入轨道。图乙为腾空过程左视图。 该运动员可视为质点，不计空气阻力，取重力加速度的大小g=10m/s2，sin72.8°=0.96，cos72.8°=0.30。 求：（1）运动员腾空过程中离开AD 的距离的最大值d；（2）M、N 之间的距离L。

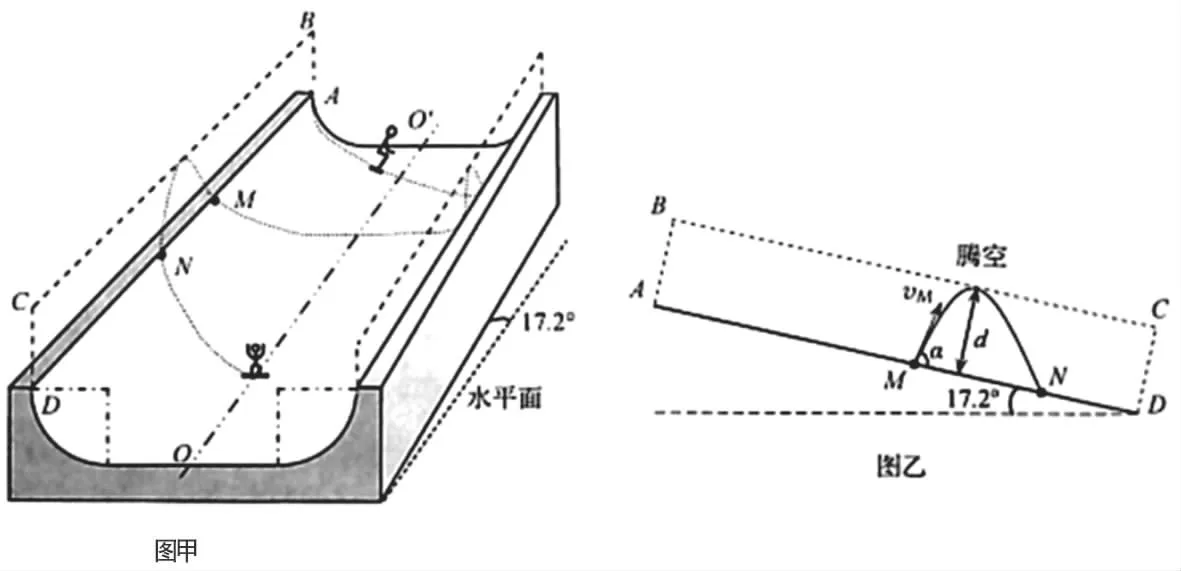
借助体育运动项目考查物理知识， 在高考命题中屡见不鲜。 本题就以单板滑雪U 型池比赛为背景，对斜抛运动进行考查。 本题的难点是从具体的体育运动项目中提炼并精准构建出斜抛运动模型。

常见的斜抛运动如图1 所示，研究时通常以重力方向为y 轴， 垂直于重力方向为x 轴，将运动分解为x 方向的匀速直线运动和y 方向初速度为v0sinθ 的匀减速直线运动如图2所示；或者如图3 所示，以初速度方向为y 轴，垂直于初速度方向为x 轴，将重力分解，得到沿x 方向的初速度为0、 加速度为gcosθ 的匀加速直线运动， y 方向的初速度为v0、 加速度为gsinθ 的匀减速直线运动。

但此题考查在运动员腾空之后如何构建斜抛模型，却需要考生根据题目“（1）离开AD 距离的最大值d；（2）M、N 之间的距离L”进行认直思考。如果生搬硬套上面的建系方法如图4、图5 所示，将给解题带来极大的不便。考生要直正理解分解的思想，其目的是对物理量进行最恰当的分解，使问题得以简化。 本题就需要以AD方向为x 轴，垂直于AD 方向为y 轴，分解速度vM和重力， 如图6 所示。 这样的坐标系似乎违背了“尽量少分解矢量”的分解法则，但却很好地遵循了“根据题目要求选择恰当的坐标系”这一原则。 在这样的坐标系中，物体腾空后的斜抛运动， 就分解成了沿AD 方向的初速度为vMcos72.8°、加速度为gsin17.2°的匀加速直线运动，垂直于AD 方向的初速度为vMsin72.8°、加速度为gcos17.2°的匀减速直线运动。 虽然这样分解的矢量个数多，运动形式复杂，但对物理量的求解过程却是最简单的。 一般解决曲线运动的思维方法是“化曲为直”，构建模型要灵活精准，如何建立平面直角坐标系，分解什么物理量，学生不能死记硬背，而要根据每道题的情况来确定。 通过这样的复习必将使考生对知识的理解更加深刻， 知识网络更加系统，起到以点带面的效果。

二、层层递进，构建物理模型

在二轮复习中， 面对构建物理模型的教学，不能只让考生知道物理模型，而要理解模型的由来， 理解模型所体现的物理思维方法。要做到这些，就需要在复习中层层深入地提炼物理模型，一步步剖析物理思维方法，引导考生从关注模型表面到理解模型的精髓。

热学中“变质量” 问题是近几年高考的热点，学生解决此类问题时颇感棘手，那么对充气、漏气这类“变质量”问题如何应用理想气体状态方程呢？ 下面我们就以热学的“变质量”问题为例，层层递进构建物理模型。

1.用较简单的“充气问题”为突破点

例1.一个篮球的容积是2.5 L，用打气筒给篮球打气时， 每次把105Pa 的空气打进去125 cm3。 如果在打气前篮球内的空气压强也是105Pa ， 那么打30 次以后篮球内的空气压强是多少？（设打气过程中气体温度不变）

这是一个最基本的“充气问题”， 温度不变，突出了“变质量”这个主要矛盾。 可以巧妙选择合适的研究对象，使这类问题转化为一定质量的气体问题。 设想将充进篮球内的气体装进一个弹性口袋，那么，当我们取篮球和口袋内的全部气体为研究对象时，这些气体状态不管怎样变化，其质量总是不变的。

【解析】设30 次打入篮球内空气的体积及篮球内原有空气体积之和为V1，篮球的容积为V2，则V1=V2+nΔV=2.5 L+30×0.125 L=6.25 L取打入空气及球内原有空气为一整体作为研究对象，即一定质量的气体，

据玻意耳定律 p1V1=p2V2

2.如果有更多物理量发生变化，比如温度变了会怎样呢？

例2.容器内装有1 kg 的氧气，开始时，氧气压强为1.0×106Pa，温度为57 ℃，因为漏气，经过一段时间后， 容器内氧气压强变为原来的，温度降为27 ℃，则漏掉多少千克氧气？

【解析】首先，选“1 kg 的氧气”为研究对象，设容器的体积为V， 据理想气体状态方程得---①。 此时已经可以求解。

但我们进一步分析，将①式变形可得

如果漏掉部分气体的压强、 体积、 温度发生变化，取漏掉部分气体为研究对象，

据理想气体状态方程可得

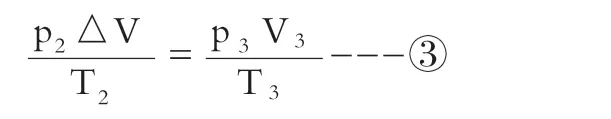
联立②③可得

有了这层理解，再来求此类问题，思路就会简单清晰。

例3.（2019 年全国卷Ⅰ33 题2 问） 热等静压设备广泛用于材料加工中。 该设备工作时，先在室温下把惰性气体用压缩机压入到一个预抽真空的炉腔中，然后炉腔升温，利用高温高气压环境对放入炉腔中的材料加工处理，改善其性能。 一台热等静压设备的炉腔中某次放入固体材料后剩余的容积为0.13 m3，炉腔抽真空后， 在室温下用压缩机将10 瓶氩气压入到炉腔中。 已知每瓶氩气的容积为3.2×10-2m3，使用前瓶中气体压强为1.5×107Pa，使用后瓶中剩余气体压强为2.0×106Pa；室温温度为27 ℃。 氩气可视为理想气体。

（1）求压入氩气后炉腔中气体在室温下的压强；

（2）将压入氩气后的炉腔加热到1227 ℃，求此时炉腔中气体的压强。

此题为充气类“变质量”问题，构建模型的关键是研究对象的选取，要保证变化前后质量不变。 由题意取10 瓶氩气为研究对象，设初始时每瓶气体体积为V0，压强为p0；使用后要保证质量不变，则10 瓶氩气分为两部分，一部分为气瓶中剩余气体的压强为p1， 体积为10V0；另一部分为压入进炉腔的气体， 设压强为p2，体积V2=0.13m3。 温度不变为室温。 在保证变化前后质量不变的条件下，对于变化后的这两部分气体， 据理想气体状态方程得 10p0V0=10p1V0+p2V2。 不用让二者压强相同先求总体积， 减去10V0后， 再利用玻意耳定律求体积V2=0.13m3时的压强p2。

通过层层递进的方式， 从简单物理情景中理解了在保证所选研究对象质量不变的情况下对两个气体状态列方程， 再进一步对压强、温度、体积不同的两部分气体进行分析，也能抓住气体初末状态保持质量不变这个关键因素，准确快速地列出理想气体状态方程。