基于雷达天线方向图的压制干扰暴露区建模
2021-03-16夏栋王守权包中华曹运合
夏栋, 王守权, 包中华, 曹运合
(1.海军航空大学 青岛校区, 山东 青岛 266041; 2.海军工程大学 电子工程学院, 湖北 武汉 430033;3.西安电子科技大学 雷达信号处理国家重点实验室, 陕西 西安 710071)
0 引言
对雷达实施压制干扰时,干扰信号从主瓣进入干扰效果是最优的[1-3]。然而在实际实施过程中出于隐蔽安全以及装备机动性的限制,被掩护目标可能与干扰机相对雷达处于不同的方向上[4-6]。根据雷达距离方程,目标回波功率大小与目标距离的4次方呈反比。当干扰机到雷达距离一定,随着被掩护目标到雷达距离的逐渐变小,目标回波功率将会超过进入雷达的干扰功率,目标将会被雷达发现。对应发现目标的临界距离称为最小压制距离或烧穿距离[7],对应目标发现区域称为雷达暴露区域[8]。文献[7-10]都对雷达暴露区的特点进行了研究和仿真,结果表明:当被掩护目标与干扰机在同一方向上时,雷达照射被掩护目标的同时干扰从雷达天线主瓣进入,烧穿距离最小;当被掩护目标所在方向与干扰机所在方向的夹角变大时,烧穿距离随夹角单调变大;当夹角角度相差180°,烧穿距离最大。这在理论上不符合雷达面天线的方向图特性,根据雷达天线方向图随角度变化的特点,烧穿距离应当随着角度变化引起的方向增益变化而振荡增加,并且雷达压制干扰试验也证明了这一点。因此,需要从理论角度分析烧穿距离随夹角的变化关系,并根据得到的结论分析被掩护目标的最优进入角度,从而达到最优的干扰效果。
1 压制干扰下雷达暴露区域建模
雷达受到压制干扰时,进入雷达的干扰信号随角度的强弱变化受到天线方向图的调制,其功率强弱与雷达天线的指向和波束形状有非常大的关系。雷达常用的天线波束形状有两种。预警或搜索雷达一般采用水平面内窄波束、垂直面内宽波束的扇形波束(或特殊的赋形波束),牺牲俯仰面上的测角精度以提高关注空域的扫描速度;火控雷达或精密跟踪雷达采用方位和俯仰上都是窄波束的针形(笔形)波束。对于搜索雷达,由于垂直面上主波束很宽,绝大部分情况下俯仰方向上天线主瓣能够同时覆盖被掩护目标和干扰机,可以只考虑方位上的角度差别;对于采用针形窄波束的精密跟踪雷达,需要对俯仰面的天线方向图单独分析,但是分析的方法与水平面天线方向图一致,因此不再单独讨论。在不影响结论的情况下,本文只考虑水平面内方位角对烧穿距离的影响,相当于距离- 方位两坐标雷达受压制干扰的情况。
在上述条件下对某雷达施加压制干扰时,设干扰机、雷达和被掩护目标的相对位置如图1所示。干扰机距离被干扰雷达的距离为Rj,被掩护目标与被干扰雷达的距离为Rt,雷达探测目标时天线主瓣对准目标,对于雷达而言被掩护目标所在方向与干扰机所在方向的夹角为θ. 当θ=0°并且Rj=Rt时,雷达受到的干扰为自卫式干扰;多数情况下Rj≠Rt或者θ≠0°,此时为支援干扰或者伴随干扰。无论是哪种情况,雷达天线主瓣对准目标探测时,到达雷达接收机的有用目标信号功率Prs可根据(1)式得到:
(1)
式中:Pt为雷达发射功率;Gt为雷达天线发射增益;Gr为雷达天线接收增益;λ为雷达发射电磁波波长;σ为目标反射截面积;Lr为雷达系统损耗。

图1 干扰机、雷达、被掩护目标位置示意图Fig.1 Locations of jammer, radar and protected target
进入雷达接收机干扰信号功率Prj计算方法[11-12]为
(2)
式中:Pj为干扰机发射功率;Gj为干扰天线增益;Gr(θ)为干扰机方向上雷达天线接收增益;γ为干扰信号与雷达系统极化失配引起的损耗;Lj为干扰信号在干扰机和进入雷达内部后的射频传播损耗;Δfr为雷达接收机带宽;Δfj为干扰信号带宽。
(3)
式中:Kj为压制系数,通常情况下认为Kj=2时,目标信号被干扰信号淹没,压制干扰有效。存在压制干扰时根据(3)式,当取Kj=2时雷达对θ方位上反射截面积(RCS)为σ的目标压制距离计算公式如(4)式所示:
(4)
需要注意的是Gr(θ)为雷达天线对准被掩护目标时干扰机方向上雷达天线接收增益。当θ=0° 时,说明干扰机跟被掩护目标在雷达的同一方向时,Gr(θ)为雷达天线的接收主瓣增益。多数情况下θ≠0°,为了简化计算Gr(θ)可以按照(5)式近似计算得到[14-15],其函数曲线如图2所示。
(5)
式中:θ3dB为雷达天线波束主瓣宽度;K为近似因子。K的取值范围为0.04~0.10[16],对于针形波束,则K取值范围为0.06~0.10,而对于波束较宽、增益较低的扇形波束,K取值范围为0.04~0.06[17].
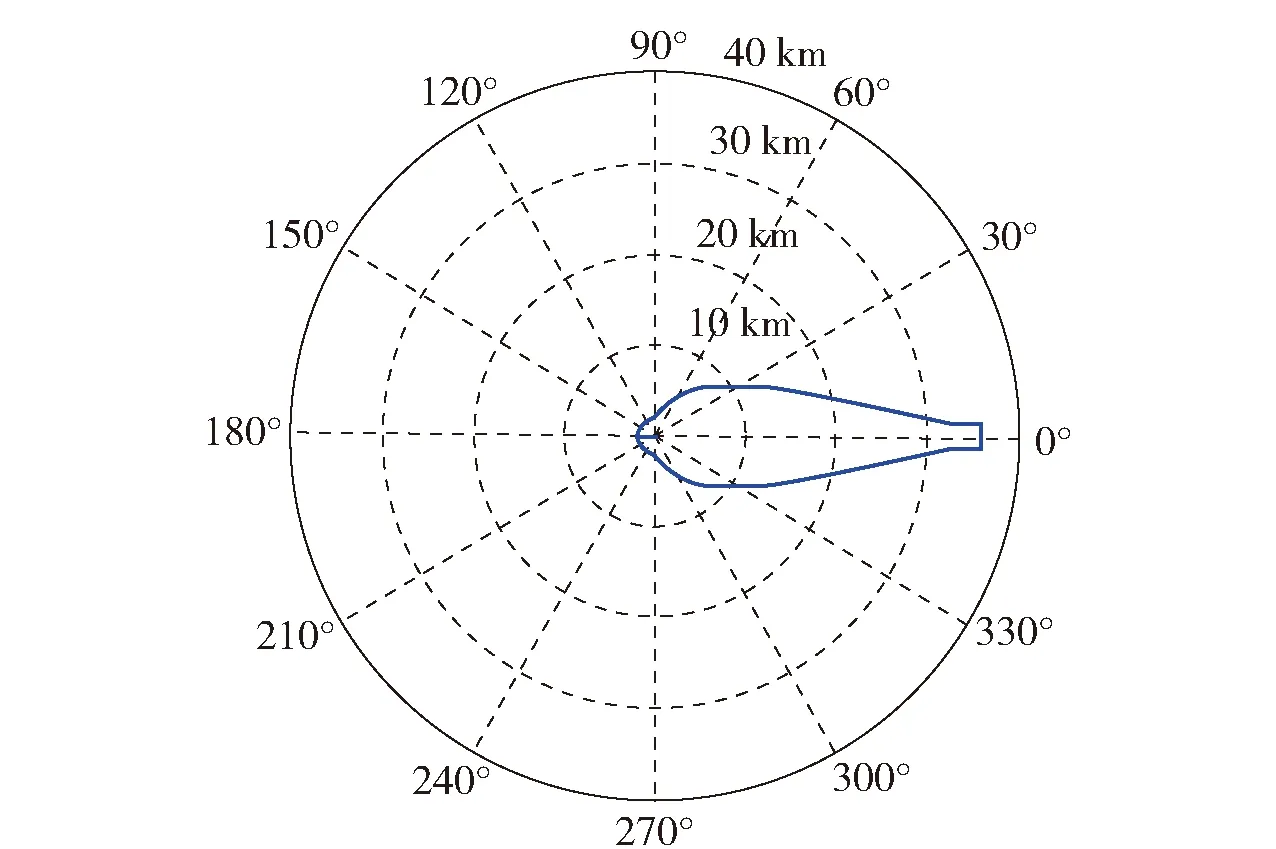
图2 Gr(θ)近似计算结果Fig.2 Approximate result of Gr(θ)
根据(5)式和雷达压制距离方程(4)式,对压制干扰的雷达暴露区域进行仿真,仿真参数取值如表1所示。设被掩护目标的RCS为5 m2,(5)式中近似因子K取0.8,压制系数取Kj=2,极化失配因子γ=0.5. 根据上述参数、(4)式和(5)式,得到目标最大探测距离随目标进入角度的关系如图3所示。
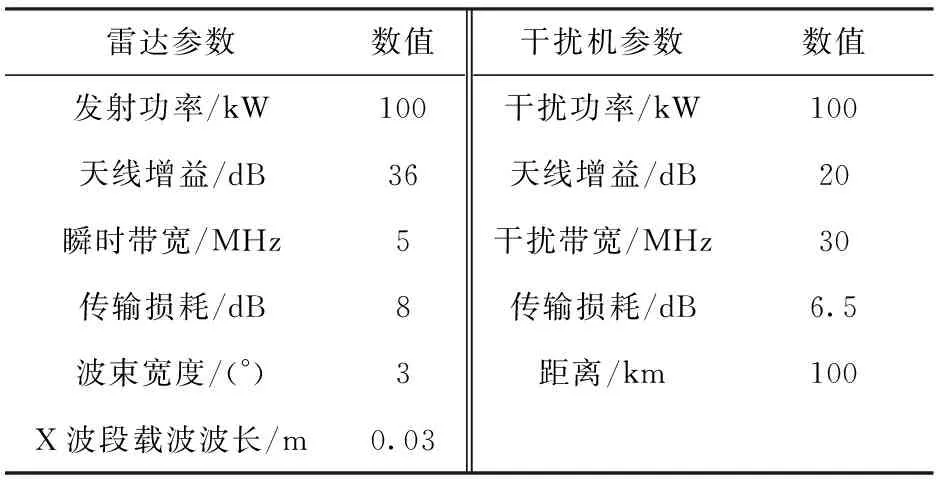
表1 雷达和干扰机工作参数
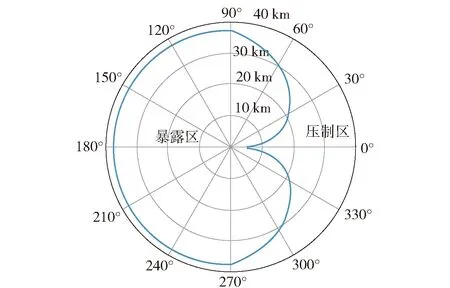
图3 进入接收机干信比对应的目标暴露区Fig.3 Target exposed area based on jam-to-signal ratio of receiver
由图3可以看出,相对于雷达的位置,当干扰机与被掩护目标的夹角θ=0°,即被掩护目标从干扰机方向进入时烧穿距离最小,烧穿距离随被掩护目标方向偏离干扰机方向角度的增大而增大,当被掩护目标从干扰机反方向进入时(θ=180°),烧穿距离最大。以上结果是基于图2所示不同方向上雷达天线接收增益Gr(θ)得出的,而实际上雷达天线不同方向上的接收增益与图2存在较大差别,导致图3的结果与实际的雷达暴露区存在较大出入。
2 雷达天线方向性建模与仿真
对于单基地雷达而言,收发共用一部天线。根据天线发射和接收的互易性,单基地雷达天线发射方向特性与接收方向特性一致。图4是某型舰载雷达天线主瓣附近3个波束宽度范围内方向特性,可以看出实际天线方向特性与图2中的近似值差别较大:真实的雷达天线方向特性为存在主瓣和副瓣的sinc函数形状,并不随着角度单调减小。这一点也可以通过雷达受压制干扰时的平面位置显示器(PPI)画面看出,如图5所示。在图5的雷达PPI画面中干扰最强的方向为干扰机所在方位(图5中为正右方),当雷达天线扫描到该位置时干扰信号从主瓣进入,天线对干扰信号提供的增益最强。当天线扫描离开该方位时,干扰信号从旁瓣进入,天线旁瓣提供的增益随偏离角度逐渐变弱,PPI中对应方位上的干扰信号也相应变弱。需要注意的是,在干扰信号随方位逐渐变弱的过程中出现了明暗相间的条纹,其中亮的条纹对应着天线旁瓣的顶点,而暗的条纹对应着天线波瓣间的零点。暗条纹处干扰信号较弱,目标清晰可见,因此应当属于雷达暴露区,这显然与图3的结果不相符。

图4 某雷达实测天线方向特性Fig.4 Measured beam pattern of a real radar antenna

图5 雷达受到压制干扰时的PPI画面Fig.5 Radar PPI display with suppressing jamming
通过进一步观察可以得到,图2只是真实雷达天线方向图主副瓣顶点的包络。当采用图2的近似值时,如果被掩护目标进入方向与干扰所在方向的夹角值不等于天线方向图主副瓣顶点对应的角度值时,特别是落在天线波瓣间零点位置时,当雷达天线主瓣对准被掩护目标探测时,干扰恰好从天线波瓣间的零点进入,干扰信号就会被抑制(如图5明亮干扰条纹间的无干扰区域),烧穿距离必然会变得很大[18]。因此,有必要对雷达天线方向特性进行精确建模和仿真。
为了得到准确的雷达天线方向特性模型,Gr(θ)应该考虑天线的主瓣增益和天线方向性函数,如(6)式所示:
Gr(θ)=G0f(θ),
(6)
式中:G0为主瓣增益;f(θ)为天线方向图函数。雷达天线采用面天线,天线方向性函数非常复杂,形状上与sinc函数相近[19],但是波束宽度和旁瓣特性却与sinc函数存在较大差别[20]。为了得到雷达天线方向性函数的精确值,本文采用sinc复合函数作为基本形状函数[21],如(7)式所示:
(7)
式中:L为天线孔径。得到的天线方向性函数基本形状如图6所示。

图6 sinc复合函数形式的天线方向性函数Fig.6 Antenna directional function with sinc function
(7)式中sinc函数的内部嵌套了sin函数,形式较为复杂,为了简化计算令κ0=λ/L,根据天线特性半功率波束宽度θ3dB=0.886λ/L=0.886κ0[21],可以得到κ0=1.13θ3dB. 同时,令φ=sinθ,将(7)式用(8)式代替,则可得f0(θ)=g0(sinθ)。
(8)
虽然(7)式提供了天线方向性函数的形状信息,但是真实雷达天线的旁瓣增益值与图6中的雷达天线参数并不相同。设雷达天线旁瓣衰减为G=(g1,…,gi,…,gn),gi为第i旁瓣衰减度,后向衰减为Gb,如图7所示。
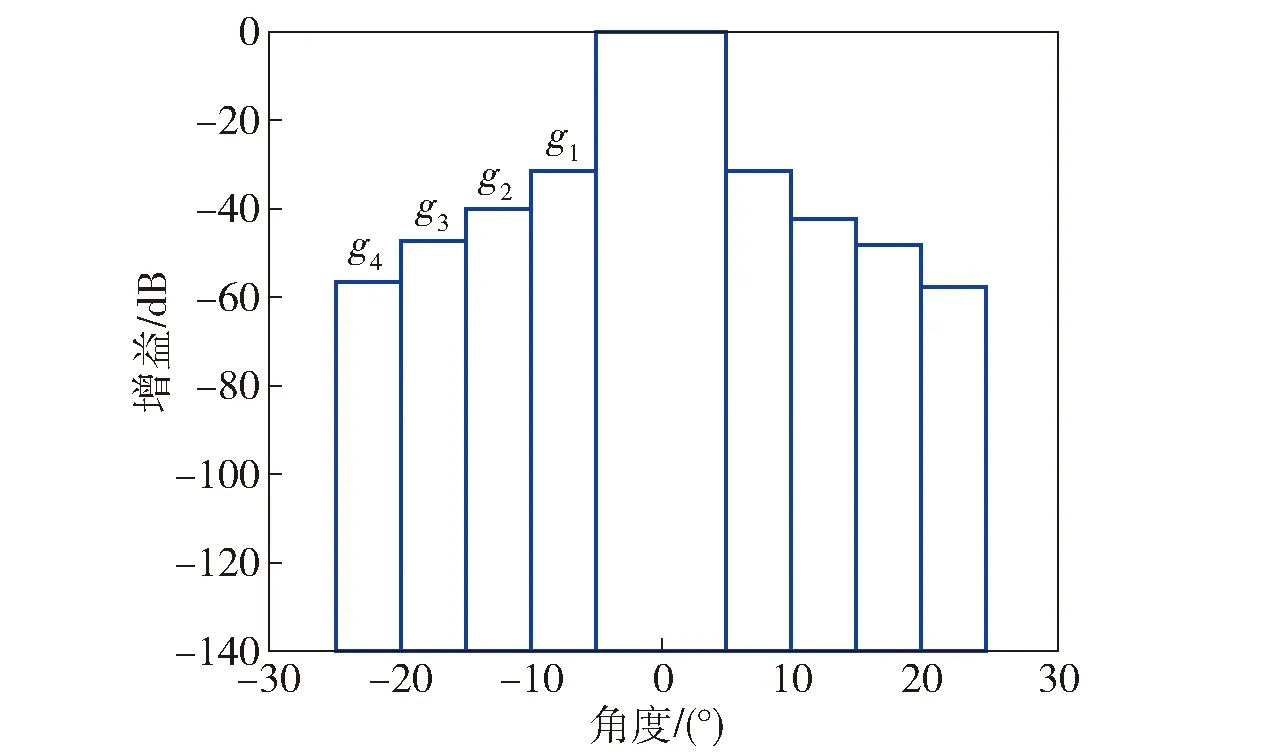
图7 天线旁瓣衰减Fig.7 Antenna sidelobe attenuation
为得到天线方向特性的准确模型,需要将图6中天线副瓣增益调整到与图7一致,采用分段函数(9)式的修正函数对(8)式进行修正:
(9)
式中:1≤i≤n,n≤j≤(π/κ0-1/2);gj为根据雷达提供数值的最后一个旁瓣增益与后向增益估算出的第j个旁瓣的增益,gj=gn-((j-n)κ0/(π-(n/2+1/2)κ0))(gn-Gb)。根据(8)式和(9)式可以得到用中间量φ表示的天线方向图函数,如(10)式所示:
g(φ)=g0(φ)ga(φ).
(10)
利用表1的雷达天线参数,并且设主瓣增益G0=36 dB,旁瓣衰减G=(-30 dB,-40 dB,-45 dB,-48 dB),后向衰减Gb=-70 dB. 根据(6)式和(10)式得到用中间量φ表示的天线方向特性曲线,如图8所示,其中主瓣和第1、第2副瓣增益与图4真实天线方向特性非常贴合。
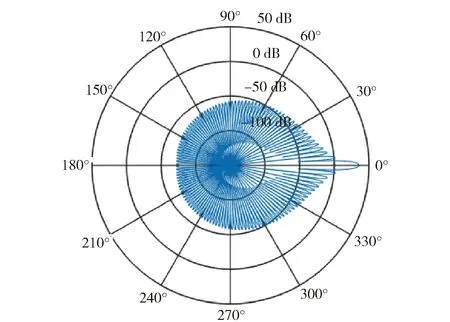
图8 极坐标下雷达天线方向特性Fig.8 Radar antenna pattern in polar coordinate
3 雷达天线方向性修正下的暴露区模型
根据天线特性模型(6)式和烧穿距离计算函数(4)式,仍然采用表1的工作参数,此时κ0=1.13、θ3dB=3.39°,仿真得到烧穿距离随中间变量φ=sinθ的关系,如图9所示。
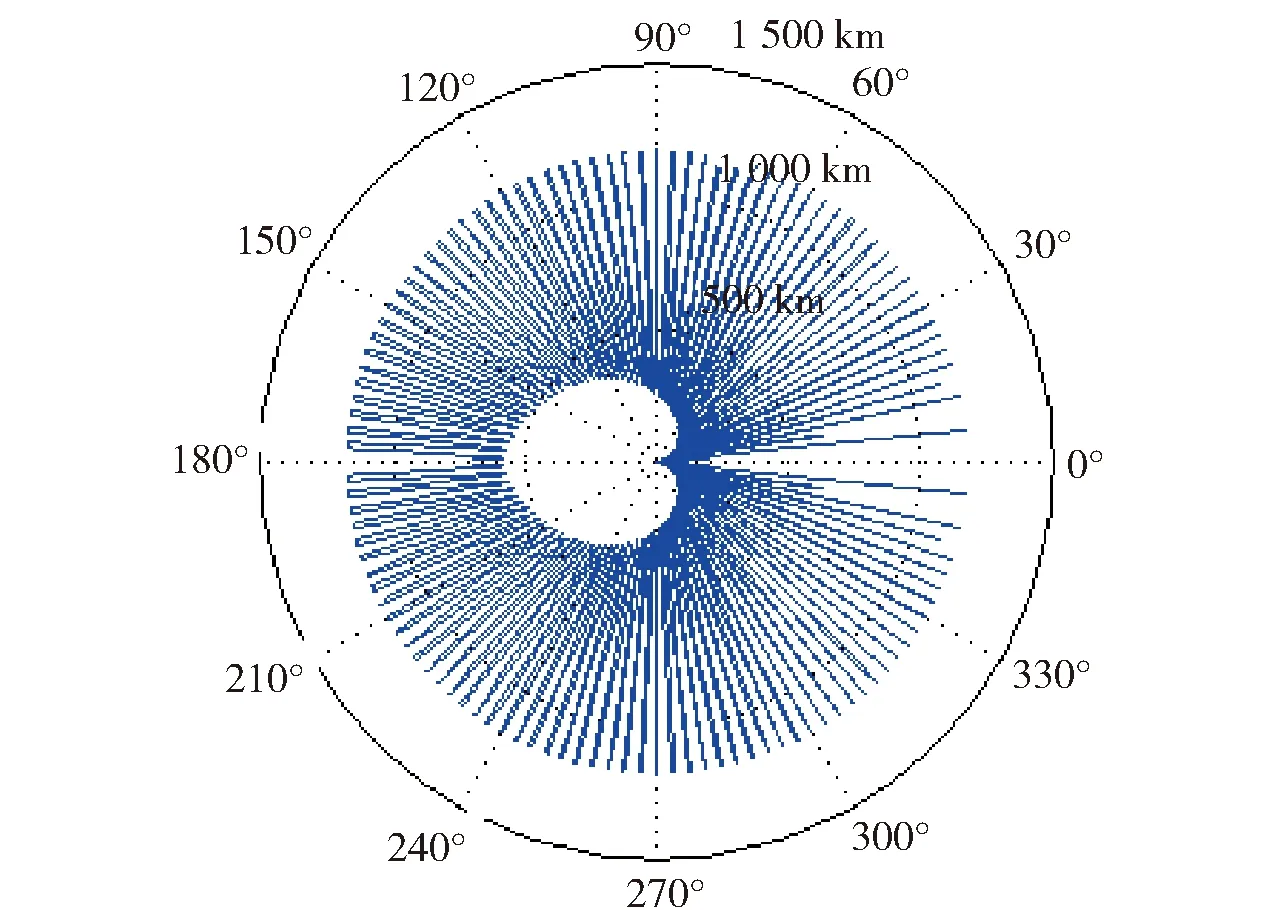
图9 天线方向特性修正下的雷达暴露区Fig.9 Radar exposed area modified by antenna beam pattern
在图9中曲线以内的区域都是雷达暴露区,即被掩护目标进入曲线以内区域将被雷达探测到。由于图3中曲线的自变量为中间变量φ=sinθ,当θ在[0 rad,2π rad]之间变化时,φ随之变化,但是变化范围限制在-1 rad≤φ≤1 rad,当角度单位用(°)表示时,φ∈[-57°,57°]。即当θ在[0 rad,2π rad]之间变化时,只利用了图8中±57°内的曲线部分。将图3和图8进行比对可以得到:
1)考虑天线方向性后,当θ在偏离0 rad时,φ随之变化,而烧穿距离并不是逐渐变大的过程,而是随φ振荡变化,并且存在密集的毛刺(烧穿距离极大值)。这一点与实际试验中烧穿距离测量随目标进入角度不规则振荡变化相符合。
2)图3中暴露区只与图9暴露区中间白色心形区域大体一致,而图9中大部分角度对应的烧穿距离要远大于白色心形区域,当采用图3 进行压制效果评估时会产生非常大的误差。
3)对比图8和图9,天线方向特性修正下的烧穿距离在随φ的振荡变化过程中,极大值出现在图8中的极小值处,而极小值出现在图8中的极大值处,这一点可以从局部放大图中更清晰地得到,如图10所示。从理论上分析,当φ处于天线方向增益的极大值时,雷达天线主瓣对准目标时干扰信号从雷达天线副瓣的极大值进入,此时进入雷达的干扰功率较强,烧穿距离较小;反之,φ处于雷达天线方向图的极小值时,雷达天线主瓣对准目标时干扰信号从天线副瓣的零值进入,干扰信号被抑制,烧穿距离较大。
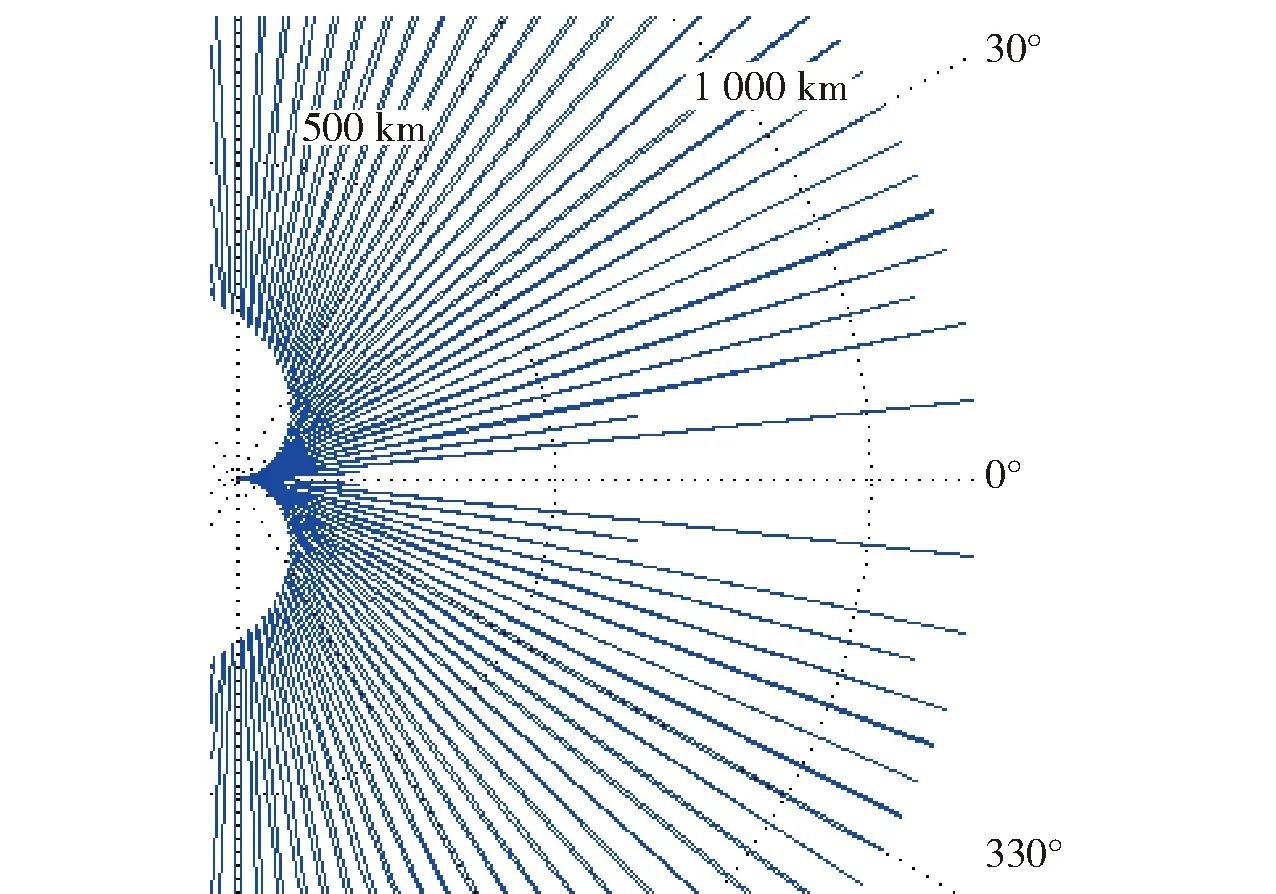
图10 雷达暴露区局部放大图Fig.10 Zoom picture of partial radar exposed area
4 压制干扰掩护目标突防方向策略研究
4.1 单部干扰机掩护目标突防方向策略
当只有一部干扰机对敌方雷达实施压制干扰时,为了达到好的压制效果,应当选择图9和图10中烧穿距离极小值对应的角度θ进行突防。由于图9和图10表示了烧穿距离随中间变量φ的变化情况,可通过先确定合适的φ值,然后根据θ和φ的关系式φ=sinθ计算出对应的突防角度θ. 突防角度θ的选择可以分为下面两种情况进行讨论:
1)由图10可以看出,当φ=0 rad时烧穿距离最小,此时θ=0 rad,即被掩护目标从干扰机所在方向进入。当中间变量φ从0 rad变化很小的角度时,即|φ|<4κ0,烧穿距离变化不大。因此,被掩护目标应当优先选择满足|φ|<4κ0对应的突防方向。根据θ和φ的关系,突防方向应满足|sinθ|<4κ0. 在雷达系统设计中,一般满足λ≪L,可以作近似运算φ=sinθ≈θ[21],因此突防方向优先选择|θ|<4κ0或|θ|<4.48θ3dB.
2)由于兵力部署和装备机动限制等原因,被掩护目标并不总能选择从干扰机附近方向进入。为了达到良好的压制干扰效果,被掩护目标的突防方向应当选择图9中烧穿距离极小值对应的角度,并且必须避免从烧穿距离极大值的方向上进入。根据(9)式和sinc函数的性质,烧穿距离极小值对应的中间变量φa应当如(11)式所示:
|φa|=(N+1/2)κ0,
(11)
式中:N取整数。此时突防方向应当尽量选择在φa对应的角度θa附近,θa可按(12)式计算得到:
θa=±arcsin [(N+1/2)κ0].
(12)
突防方向的选择要求被干扰雷达位置固定,并且干扰机和被掩护目标不能作切向上的运动。实际中,可能雷达平台是运动的,如机载雷达和舰载雷达,并且被掩护目标和干扰机平台也可能作切向上运动。在上述情况下对于被掩护目标而言,由于θ随时间变化引起中间变量φ随时间变化,最终引起烧穿距离随时间起伏,导致目标被间断性地发现。为了避免目标被间断性发现,可以采取多部干扰机对雷达进行压制干扰。
4.2 多部干扰机掩护目标突防方向策略
当存在N部干扰机同时对雷达进行干扰时,雷达接收到的干扰功率为多部干扰机各自进入雷达系统的干扰功率之和。根据(2)式,雷达接收到的干扰总功率可由(13)式得到:
(13)
再根据(1)式和(3)式,压制干扰有效应当满足(14)式:
(14)
此时的烧穿距离计算公式如(15)式所示:
(15)
为简化计算,考虑2部干扰机的情况,两部干扰的参数仍如表1所示,2部干扰机所处方位不同,θ2=θ1+Δθ,如图11所示。为简化计算,设第2部干扰机布置于θ2=0 rad方位、第1部干扰机布置于θ1=-Δθ,同时仍然引入中间变量φ=sinθ进行分析。根据θ和φ的关系,可以得到φ2=0 rad,φ1=sin (-Δθ)=-Δφ. 两部干扰机距离雷达的距离均为200 km,两部干扰机所在方位角度差对应的中间变量Δφ发生变化时,雷达暴露区变化如图12所示。
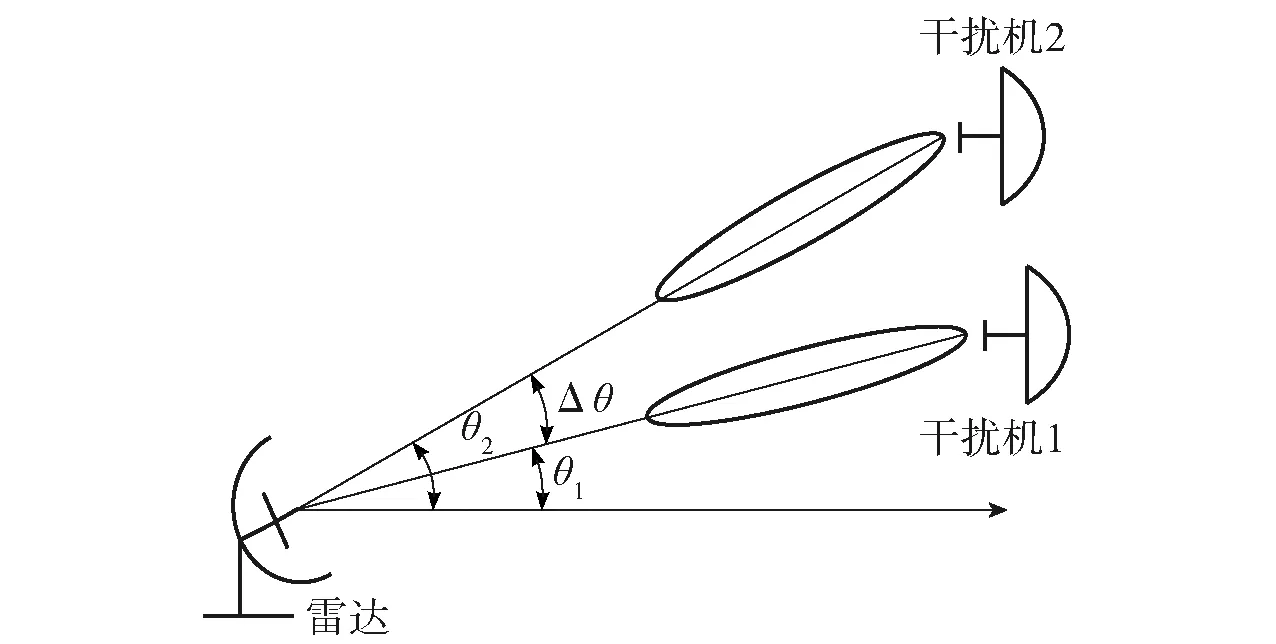
图11 2部干扰机同时实施压制干扰位置关系Fig.11 Location relationship of 2 jammers for suppressing jamming
由图12可以看出,当采用2部干扰机同时对雷达实施压制干扰时存在以下规律:
1)同单部干扰机类似,雷达烧穿距离随被掩护目标突防方位振荡起伏,存在较多的极大值和极小值。
2)当中间变量φ的角度差Δφ的取值满足Δφ=Nκ0时,雷达暴露区域毛刺密集,仅φ=0 rad和φ=-Δφ两个值附近非常小的角度范围内烧穿距离较小。但是当Δφ持续变大时,φ=0和φ=-Δφ之间的角度以及背向角度(即旋转180°),烧穿距离有明显的下降,见图12(e)、图12(g)、图12(i)、图12(k)和图12(m)。
3)当Δφ=(N+1/2)κ0时,若N值较小时雷达暴露区非常理想,尤其是干扰机所在方位附近的角度区域内。随着N取值和Δφ变大,雷达暴露区毛刺增多,烧穿距离的极大值出现频率显著增加。
根据图12中雷达暴露区规律,为提高干扰压制效果,2部干扰机的布置方位应当遵循以下策略:
1)当满足Δφ<10κ0,且Δφ的取值在(N+1/2)κ0附近(严格避免出现Δφ=Nκ0)时,φa在[-10κ0,0]范围内任意取值,烧穿距离都非常小,压制干扰效果最好。对应阵位角度要求为:Δθ 2)当Δφ≥10κ0,即Δθ≥arcsin (10κ0)时,也可以取得较小的烧穿距离,但是要求突防方向对应的中间量要满足φa=(N+1/2)κ0,因此突防方向应满足θa=arcsin [(N+1/2)κ0]。 3)当Δφ≥10κ0且不满足φa=(N+1/2)κ0时,也可以取得较小的烧穿距离,此时突防方位选择任意一部干扰机所在方位,并且干扰机配合布站满足Δφ=(N+1/2)κ0,即Δθ=arcsin [(N+1/2)κ0],如图12(j)和图12(l)所示。 对雷达实施压制干扰时,被掩护目标选择正确的突防方向可以有效提升干扰效果,被掩护目标应当优先选择从干扰机所在方位附近较小的角度范围内突防。当现实情况不允许从干扰方向突防时,对于只有一部干扰机的情况,突防方向应选择利用雷达天线方向图特性,从天线旁瓣顶点位置进入,即θa=±arcsin [(N+1/2)κ0]。对于存在多部干扰机时,干扰机位置布署满足Δθ≈arcsin [(N+1/2)κ0]且Δθ5 结论
