基于旋转阀的固体火箭发动机燃烧室压强振荡特性

2021-03-16席运志王宁飞李军伟张智慧

兵工学报 2021年1期

席运志，王宁飞，李军伟，张智慧

(北京理工大学宇航学院, 北京 100081)

0 引言

固体火箭发动机(SRM)出现的燃烧不稳定，通常伴随燃烧室内压强不规则振荡[1]。极端情况下，可能导致SRM在飞行过程熄火或爆炸，直接影响其总体飞行性能。因此，在SRM设计过程有必要对其内弹道特性和固体推进剂燃烧稳定性进行评估[2-3]。

对于SRM内弹道特性，可通过流场仿真[4]或内弹道方程[5]计算获取。然而，对于固体推进剂，因其具有组分复杂、燃烧环境恶劣等特点，目前尚无完备的理论模型可以精确预估其燃烧稳定性。当前主要通过实验的方式获取压强耦合响应函数，对固体推进剂的燃烧稳定性进行预估[6-7]。在现有测试方案中[8]，由于T型燃烧器及其改进方案[9-12]具有结构简单、操作方便等特点而被广泛应用，但其也存在费用高、理论不完备、测试误差高达30%～50%、不易开展低频实验等缺点[6]。为克服T型燃烧器存在的上述不足，文献[13-15]提出旋转阀法，该方法将小型SRM和旋转阀装置相结合，具有测试频域广、经济适用性好、测试结果最接近实际SRM等优点[6]，是T型燃烧器的一种良好替代或补充方案。

但旋转阀法对测控系统精度要求极高，需精确测量燃烧室内压强振荡与旋转阀有效排气面积变化之间的相位差。该相位差直接决定实验测试结果的准确性。为此，Brown等[13]采用接触式测量方法直接获取有效排气面积变化，但存在磨损以及高频工况下误差大等缺点。由于缺少面积测量的相关改进方案，致使旋转阀法目前仍未被广泛使用，尤其是国内缺少对旋转阀法的相关实验及仿真研究。现阶段SRM中出现的燃烧不稳定多为低频[16]，鉴于T型燃烧器对低频测试的不足，亟需开展旋转阀法相关研究，了解旋转阀工作过程，优化旋转阀系统设计并提出准确相位角测控方案。

为进一步了解旋转阀有效排气面积变化与燃烧室压强之间的关系，本文首先搭建一套基于旋转阀的冷流实验系统，并推导了有效排气面积变化及燃烧室压强理论计算模型。同时，基于动网格技术[17-19]和ANSYS/Fluent软件平台建立了旋转阀工作过程的三维瞬态流场仿真模型(简称仿真模型)，该模型使用自定义函数(UDF)将旋转阀转动运动等效为周期性的摆动运动，用于开展内流场仿真与可视化研究。最后，通过实验、理论模型及仿真模型之间的相互对比，验证了理论模型和仿真模型的有效性。为研究旋转阀压强振荡及流场特征提供了新的思路和方法，也进一步为热流实验中开展燃烧室压强相对于有效排气面积的相位角测量方案研究及旋转阀改进设计工作奠定实验基础及理论验证方法。

1 实验方法和理论模型

1.1 实验装置

基于旋转阀的冷流实验装置如图1(a)所示，主要组成部分包含高压氮气瓶、燃烧室、旋转阀和数据采集仪。实验中，将高压气体经减压阀降低至实验需求压强，而后经减压的气体进入燃烧室和旋转阀。在减压阀和燃烧室之间有压强计和电磁阀，压强计用于测量实际供气压强，电磁阀用于控制气流的供给。其中，燃烧室内径为72 mm，体积为320 cm3. 实验主要流程为，先启动旋转阀并达到预定转速，然后打开电磁阀开关，对燃烧室进行供气，燃烧室内压强变化由数据采集仪采集。图1(b)中RED为转子排气通道，SED为定子排气通道。

图1 冷流实验装置和旋转阀示意图Fig.1 Schematic diagrams of cold-flow device and rotary valve

旋转阀转速范围介于0～3 000 r/min，其内部结构剖视如图1(b)所示，主要由转子、转子轴、定子、联轴器、伺服电机等组成。其中，转子与定子为石墨材质，转子轴为中空轴，其材质为钢。转子和转子轴装配在一起形成转动部件同步转动。同时，转子与伺服电机由联轴器连接，伺服电机运转由伺服执行器控制，即转子转速实际由伺服执行器控制。转子外径为76 mm，在转子中心位置，沿其周向等间距开有16个半径为1.5 mm的RED. 定子与燃烧室装配在一起，燃烧室内高压气体可以通过定子中心位置的SED排气。其中SED与RED位置中心对齐，为消除谐波组分[13]及安装精度因素的影响，SED截面形状设计为矩形，其长为4.5 mm，宽为3.0 mm. 在转子转动过程，16个RED与SED形成周期性的排气通道，使得高压气体可从燃烧室经SED与RED周期性的排出，引发燃烧室内压强振荡，压强振荡频率由转子转速决定。因此，通过控制供气压强和转子转速，可引发燃烧室内产生不同工作压强和振荡频率的压强振荡。实验中，供气管路的压强由杭州美控自动化技术有限公司产P300压强计(量程0～10 MPa)测量，燃烧室内的压强由西安杰诚传感器测控技术有限公司产CYG4100高频压强传感器(量程0～4 MPa)获取。压强传感器采集的压强数据及伺服电机转动信号分别通过线路1、线路2传输给江苏东华测试技术股份有限公司产DH5922D数据采集仪(16通道)。该采集仪兼具数据采集和分析的能力，最大采样频率200 kHz，实验中使用采样频率为20 kHz.

1.2 理论模型

1.2.1 有效排气区域面积求解模型

旋转阀工作过程如图2所示，转子旋转使得RED与SED之间形成周期性的排气通道，燃烧室内高压气体从该通道排出引起压强周期性振荡。排气通道的开- 闭由SED与RED交界面形成的有效排气区域表征(见图3)。当有效排气区域面积Se大于0 mm2时，则表示排气通道打开，反之关闭。为了解旋转阀工作过程燃烧室内压强振荡与Se和转速r之间的关系，本文对旋转阀工作过程进行了理论建模。

图2 旋转阀转动示意图Fig.2 Motion of rotary valve

图3 有效排气区域随时间变化示意图Fig.3 Schematic diagram of effective exhaust region

(1)

式中：ω为角速度，ω=2πr，r为转速(r/min)；Dr为转子外径(mm)。

为定量描述非排气阶段与排气阶段行程对燃烧室压强振荡的影响，引入行程比：

(2)

本实验转子上有16个RED，每个排气周期对应行程比ΩL为1.485，则一个完整排气周期时长满足：

(3)

由图2和图3可知，Se随转子的转动呈周期性变化。在一个排气周期内，非排气阶段(A0→A1)，Se为0 mm2. 对于排气阶段(A1→A5)，Se变化关于A3位置对称(见图3)，其由0 mm2(A1)逐渐增加至1/2Se,max(A2，其中Se,max代表Se最大值)、Se,max(A2)而后逐渐减小至1/2Se,max(A4)、0 mm2(A5)，然后再次进入非排气阶段。下一个RED重复上述变化规律(A0至A5)进行周期性排气。

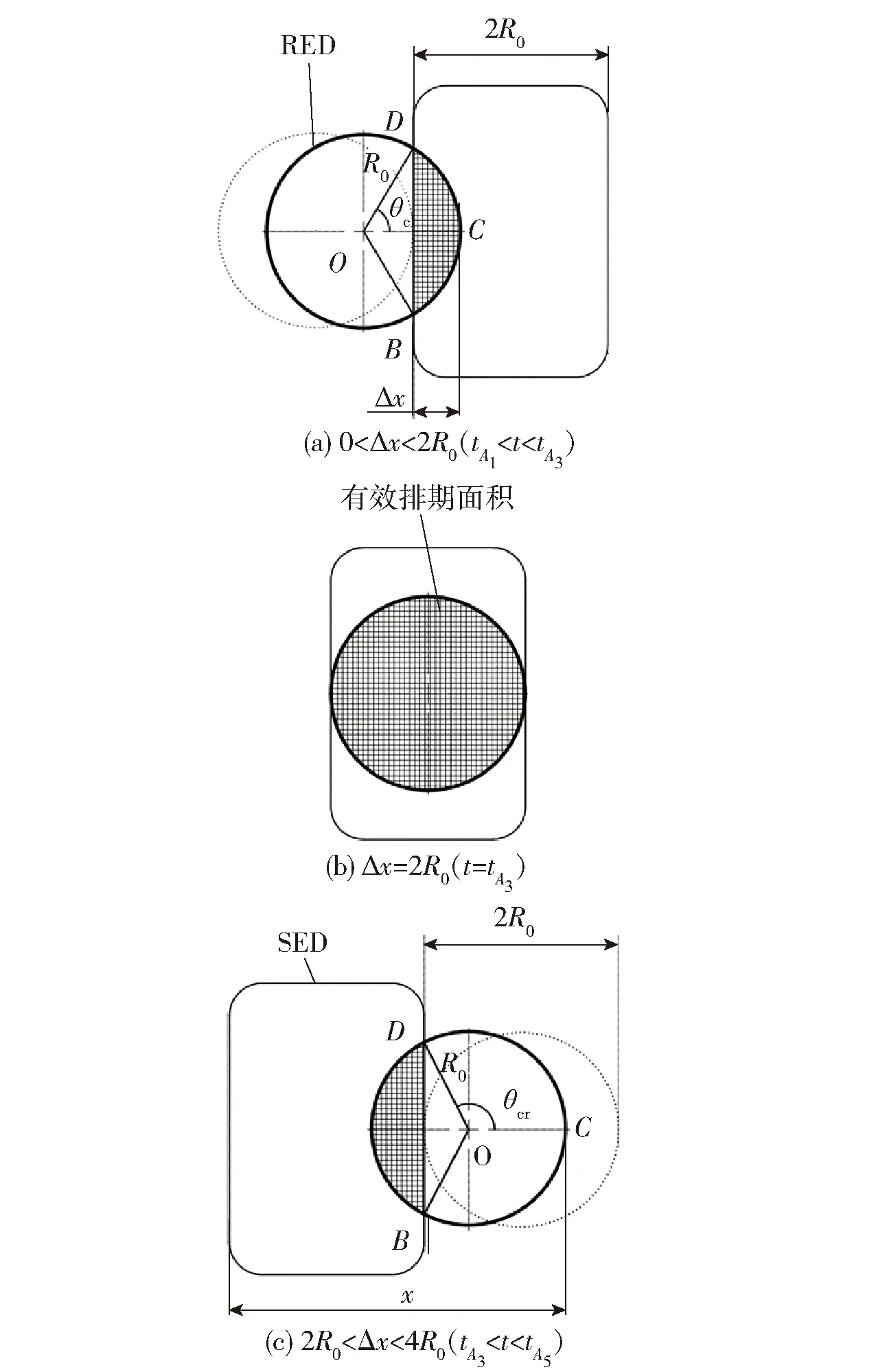
图4 有效排气面积求解示意图(排气阶段)Fig.4 Schematic diagram of solution of effective exhaust area (exhaust phase)

在一个完整排气周期内，Se直接影响排气量，进而影响燃烧室内压强波动幅值，其大小由有效排气区域的位置决定。Se的求解示意如图4所示，其中Δx=vr(t-tA1)为RED在排气阶段转过的弧线距离，tA1及tA5(同图3)分别为排气阶段开始和结束的时刻。

在Δx介于0～2R0，即tA1

(4)

θcl=arcos(1-Δx/R0).

(5)

因为Se变化关于Δx=2R0位置对称，因此，在Δx介于2R0～4R0，即tA3

(6)

θcr=arcos(3-Δx/R0).

(7)

本模型中，转子上有16个RED均匀的分布在转子圆周上，因此Se呈周期性变化，基于(1)式～(7)式，可以推导旋转阀转动过程Se随时间变化规律：

(8)

(9)

式中：n为排气周期数。

1.2.2 压强振荡求解模型

根据质量守恒定律，可建立旋转阀转动过程Se与压强振荡之间的理论计算模型。燃烧室中的气体动态质量变化由(10)式定义：

(10)

根据对2017届高三8个应届文科班实施了“201010”课堂模式的339人进行问卷调查，调查问卷发放339份，收回339份，回收率100%，全部有效。

(11)

(12)

Cd为排气流量修正系数[21-22]，

(13)

γ为气体比热比。

结合理想气体状态方程pV=mRgTg，将(11)式～(13)式代入(10)式，得

(14)

式中：V为燃烧室自由容积。

基于(14)式可计算旋转阀转动过程中转子转速r、行程比ΩL、RED半径R0及供气压强pin等参数对燃烧室压强振荡规律的影响。冷流实验中主要参数如表1所示。

考虑到通过实验方式开展不同参数对燃烧室压强振荡影响规律研究，具有成本高、操作复杂及获取有效数据点有限等缺点，以及理论模型存在无法获取旋转阀内部瞬时流动细节、流场结构特征等不足。为进一步解决实验和理论模型存在的上述问题，本文同时基于旋转阀实验装置(见图1)建立了三维瞬态流场仿真模型，该模型能够提供更加全面的三维流场可视化信息及流动细节，便于开展旋转阀转动过程压强振荡特性研究。

表1 冷流实验中主要参数

2 仿真模型

2.1 物理模型

由图2可知，当旋转阀工作时，在一个排气周期内，转子上的16个RED仅有一个进行排气, 其余处于非排气状态。如果仿真模型对16个RED同时进行计算，则计算量非常大。为了缩短计算时间，降低计算费用，本文将16个RED单向旋转运动等效为一个RED左右摆动运动，其摆动模型如图5所示，其中Ⅰ、Ⅲ分别表示RED在摆动过程的左右极限位置，Ⅱ为SED与RED中心对正时的位置。

图5 RED摆动模型示意图Fig.5 Schematic diagram of swing model of RED

在摆动模型中，RED摆动周期及线速度大小分别为T和vr与旋转运动一致，其左右极限位置与SED中心线夹角θs均为vrT/2Dr. 摆动过程，RED依次经过位置Ⅰ→位置Ⅱ(见图5(a))→位置Ⅲ(见图5(b))向左摆动完成一个排气周期，而后向右摆动依次经过位置Ⅲ→位置Ⅱ(见图5(c))→位置Ⅰ(见图5(d))，进入下一个排气周期，循环往复，实现周期性排气。因此，该摆动模型可以模拟多孔转子转动引起的周期性排气过程。

2.2 网格生成及边界条件

使用Solidworks软件构建旋转阀内部流体域的三维几何模型，而后将其导入ANSYS/ICEM软件对流体域进行网格划分。该流体域主要包含3部分：燃烧室域(含SED)、环境域及RED域，仿真计算中前两者处于静止状态，而RED按照摆动模型进行运动。由于涉及RED摆动域，且RED在摆动过程与SED存在非接触时段(见图5(a))。因此，三者网格需独立划分，最后通过网格融合技术[17]进行装配。

对于流场仿真，计算域网格质量是准确获取计算结果的关键因素[17,23]，而网格模型划分类型决定了网格划分难度及仿真计算时间。针对燃烧室，由于其几何结构相对复杂，本文主要采用四面体非结构网格对其进行网格划分，并在近壁面添加3层边界层，边界层第1层网格宽度为0.2 mm，网格总数约50万。

相对于燃烧室尺寸，其压强入口Inlet及SED的尺寸较小，为保证计算精度同时减少网格数量，对上述两区域附近的网格进行局部加密处理，如图6(a)所示。由于RED处于摆动状态，最大速度和压强梯度将出现在有效排气区域(重叠面1)附近，同时考虑到非结构网格具有无序性，为便于后期对附近流场数据进行分析和处理，将SED下部与RED接触的部分采用六面体结构网格进行划分，并对结构网格和非结构网格交界面进行节点对齐保证数据传递的连续性，如图6(b)所示，图中YL为RED的无量纲长度。

图6 计算域三维网格划分Fig.6 Topology of 3D mesh

图7 有效排气区域网格示意图Fig.7 Mesh of effective exhaust region

图8 RED三维运动(局部)示意图(从位置Ⅲ到Ⅱ)Fig.8 Mesh position of RED in swing process (from Ⅲ to Ⅱ)

将生成的计算域网格导入ANSYS/Fluent软件平台中对图6所示边界进行定义，具体如下：

1) 进气口: 此边界设置为压强入口，与实验装置的供气管路入口位置一致。其数值大小等于经减压阀后的高压气体压强，方向垂直于边界。

2) 压强出口：此边界设置为压强出口，出口压强与大气环境一致为0.1 MPa，其余流场参数由空间内部迭代计算获取。

3) 有效排气区域(重叠面1，EER)：定义RED上表面及SED下表面边界类型为干涉面(见图7)。流场仿真过程采用动网格技术[17,24]和自UDF[18]相结合的方式实现RED左右摆动(见图5)。当RED处于排气阶段时，RED上表面与SED下表面局部重叠形成有效排气区域，重叠部分自动识别为内部边界，非重叠部分自动识别为壁面[17, 19]，即来自燃烧室内的高压气流可从SED经有效排气区域流入RED，但不能经非重叠区域的干涉面进入RED. 同样的，当RED处于非排气阶段时, RED上表面和SED小表面不发生重叠，均自动识别为壁面。同理，重叠面2定义同重叠面1.

4)壁面: 除了上述边界条件外，其余表面均设定为无滑移壁面。

2.3 湍流模型

在旋转阀工作过程，RED处于周期性的摆动状态，来自燃烧室的高压气流在RED内部以自由剪切流和受壁面效应强烈影响的壁面边界流[24]并存的形式流动，且在有效排气区域附近的流场压强及马赫数变化最剧烈。为准确获取流场变化，需根据流场雷诺数确定流动类型。考虑到旋转阀的几何结构及流体介质的物理参数，可获取雷诺数Re的变化范围：从非排气阶段的最小值0至排气阶段的最大值16 000，即部分阶段的流动类型为湍流流动。

本文流场仿真基于ANSYS/Fluent软件平台展开，其提供了多种可选择的湍流模型[17]。根据旋转阀的工作特点以及前人的相关研究[17,19-20,24]，本文采用的湍流模型为RNGk-ε模型，该模型可给出有效排气区域两侧的湍流量预估值，并且能够正确估计高压自由射流和壁面的边界区域[25]，这对确定RED内部流动特性具有重要意义。与此同时，理想的可压缩气体模型、能量方程及基于压力基的求解器也一并被采用。对于控制方程，本文采用有限体积法对其进行离散化处理。对于扩散相，采用一阶差分法；对于对流、湍流动能及湍流耗散率则采用一阶迎风格式进行处理。基于上述求解方法，同时设定了以下收敛标准：除了能量残差的绝对值等于10-6外，其余均为10-4. 对于瞬态流动，时间步长与转子转速相关，其变化范围为10～2 μs.

针对瞬态流场计算中的RED摆动问题，最合适的策略为UDF和动网格技术相结合的方案[17-19]。RED摆动过程其附近及内部流场参数可由(15)式求解：

(15)

式中：ρ为密度；u为流场速度矢量；ug为动网格运动矢量；Γ为扩散系数；Sφ为源相。

在仿真计算中忽略次要因素的影响，譬如RED与SED之间的漏气、转子转速误差等。为进一步获取流场内部数据，在计算域的不同位置分别设置了压强监控点p1、p2、p3及质量流率监控面：进气口、有效排气区域,如图6所示，其中监控点p1位置和实验测压点一致。

3 仿真模型有效性验证

为节省流场仿真计算时间，本文采用摆动模型(见图5)代替单向旋转运动。为验证简化方法可行性以及仿真模型的准确性，首先采用仿真模型对转子周期性摆动进行了计算，并将摆动运动中有效排气面积变化与理论模型相比较。其次，采用冷流实验和理论计算方法获得了旋转阀转动引起的燃烧室内压强振荡，并与流场仿真结果进行对比。

本节有效性验证主要开展了3种排气频率f分别为20 Hz、100 Hz及300 Hz的验证实验、理论及流场仿真计算，具体如表2所示。除表2中参数外，其余条件相同：供气压强pin为2.15 MPa，流体介质为氮气，RED半径为1.5 mm.

表2 有效性验证工况

图9 RED周期性摆动的UDF逻辑框图Fig.9 UDF logic diagram for periodic swing of RED

图10 有效排气面积及质量流率随时间变化Fig.10 Variations in mass flow rate and effective exhaust area with time

对于仿真模型的有效性验证，本文针对工况1～工况3分别开展了冷流实验和理论计算，获取了燃烧室内p1位置的压强振荡数据并与仿真结果对比，如图11(a)所示，其中pmax和pmin分别为压强最大值和最小值。由图11(a)可知，3种方法获得的压强曲线同步变化，均由压强最小值上升至供气压强，而后维持不变，最后再减小，呈周期性变化。其中仿真计算中监控点p1～p3处的压强数值及变化规律一致，即燃烧室内压强处于整体振荡状态。因此，后续将采用监控点p1处数据开展压强振荡规律研究。

对于工况2和工况3，理论模型和仿真计算获取的燃烧室内压强最大值均无法达到供气压强2.15 MPa，说明转速(或排气频率)影响压强振荡幅值。同时，由于实验中采用减压阀手动控制供气压强，因而存在误差，比理论计算和瞬态流场仿真供气压强高约0.01 MPa. 进一步对图11数据进行处理，获取燃烧室压强振荡表征参数，如表3所示，ε为压强振荡幅值比，

图11 燃烧室内压强随时间变化曲线Fig.11 Pressure oscillation in combustor vs. time

(16)

式中：Δp为压强峰- 峰值，Δp=pmax-pmin.

表3 压强振荡表征参数

由表3可知，对于工况1，3种方法对应燃烧室最大压强pmax均能达到供气压强，实验排气周期T比理论和仿真计算多0.15 ms，误差小于1%. 同时，理论和仿真计算的压强峰- 峰值Δp较接近约0.04 MPa但比实验值0.058 MPa小。对于工况2和工况3，3种方法对应燃烧室最大压强pmax均未能达到供气压强，两种工况的实验排气周期T比理论和仿真计算分别多0.11 ms和少0.01 ms，误差约1%. 同时，3种方法获取的压强峰- 峰值Δp基本一致，分别约为0.01 MPa和0.005 MPa. 由上分析可知，本文建立的瞬态流场仿真模型是有效的，可利用其进一步开展不同工作条件下燃烧室压强振荡特性研究。

4 旋转阀工作过程仿真分析

本节以工况2为例, 对旋转阀工作过程进行瞬态流场仿真，获取了燃烧室内压强、质量流率变化曲线以及典型时刻的流场马赫数、压强分布云图。

图12 质量流率及燃烧室压强曲线Fig.12 Variations in mass flow rate and pressure with time

在旋转阀工作期间RED位置不断变化，有效排气区域附近的流场参数变化剧烈，进一步获取图12中典型时刻t=46.3 ms、47.98 ms以及有效排气区域面积为1/2Se,max对应时刻46.97 ms的流场马赫数Ma及压强分布云图，如图13所示。在t=46.3 ms时，RED刚进入非排气阶段，其与SED下表面部分重叠，高压气流在RED内部形成超音速气流，最大马赫数约3.2. 随着有效排气区域面积的增加，在t=46.97 ms时，SED内压强减小，RED中最大马赫数降为2.6且在RED内部形成旋涡。而到了t=47.98 ms时，有效排气区域面积达到最大值，此时净排气质量也达到了最大值，SED内部压强继续减小，RED最大马赫数降为1.2.