Aeroelastic analysis and structural parametric design of composite rotor blade
2021-03-16LiMAQijunZHAOKaiZHANGXiayangZHANGMengmengZHAO
Li MA, Qijun ZHAO, Kai ZHANG, Xiayang ZHANG, Mengmeng ZHAO
National Key Laboratory of Science and Technology on Rotorcraft Aeromechanics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
KEYWORDS Aeroelastic stability;Composite material;Cross-section analysis;Hub loads;Inverse design;Rotor
Abstract Based on FEM theory,a method of dynamic analysis for hingeless rotors considering anisotropiccompositematerialsisestablished.Aparametricmodelingmethod ofcompositebladewithtypical profile and high simulation degree for design is proposed.Through the finite element method,the profile characteristicsofrotor blade can beobtained efficiently and accurately,and the synchronization of parametricdesignandfiniteelementanalysisofstructuralcharacteristics canberealized.Then a23-degreesof freedom non-linearbeamelementisused tosimulate the extended one-dimensional beam,therebyanonlinear differential equation describing the elastic motion of the rotor is established.To obtain the crosssectional target characteristics of the blades,aninverse design methodis proposed for cross-section components based on combinatorial optimization algorithm.The calculation and validation work show that the proposed model can effectively analyze the aeroelastic characteristics of general composite rotors.Further,the influenceofcross-sectionalparametersonthe aeroelastic stabilityand hub loadsofhingeless rotor is analyzed and some remarkable conclusions are obtained.
1. Introduction
The traditional metal hinged rotor cannot meet the specifications of modern helicopter design. Composite hingeless rotors retain the advantages of long fatigue life and easy dynamic tailoring, with good maintainability and excellent flight performance that traditional rotor does not have, the composite rotor has attracted more and more attention. However, this type of rotor also has a significant disadvantage,that is,aeroelastic instability,which can be avoided by adjusting the parameters of blade composite cross-section components. Therefore,it is of intense value to study the influence of composite components on aeroelastic stability of hingeless rotor.1
Because of the elastic coupling among the flapping,lagging and torsional degrees of freedom of composite hingeless rotor,the finite element method is generally used to establish the analysis model. Considering the large elastic deformation of the blade, the geometric nonlinearity must be taken into account in the model. In addition, the use of composite materials also increases the difficulty of stability analysis, so the aeroelastic stability of composite hingeless rotor is very difficult.A qualitative analysis is much more complicated than traditional rotor analysis. It was not until 1985 that Hong and Chopra2first carried out stability analysis of composite hingeless rotors.However,the two-dimensional cross-section analysis has limitations, and the one-dimensional beam model only adds some of the coupling terms to the analysis of the same blades. The finite element adopted has traditional 15 Degrees of Freedom (DOF). Subsequently, Smith and Chopra3improved the beam model on this basis, using a new 19-DOF beam, including the shear DOF which is very important for the modeling of composite rotor, but the two-dimensional section is still analyzed by analytical method.Freidmann et al.4also carried out the correlation analysis.Two-dimensional section used finite element analysis based on Saint Venant’s principle, which improved the analysis ability of complex section.One-dimensional beam uses 23-degree-of-freedom beam element to model more accurately. In 2006, Friedmann et al.5used single-chamber and double-chamber blades,and replaced the original two-dimensional section analysis with more accurate VABS (Variational Asymptotic Beam Section Analysis)analysis, thus improving the accuracy of aeroelastic stability analysis.In addition,Fulton and Hodges6have also conducted relevant studies,and the influence of ply angle on stability was analyzed. In 2009, Stuart and Nicholas7established the parametric model of BERP IV blade.Composite material coupling layer was laid on the inside of the blade, and the effect of the coupling stiffness of the inner wall on the dynamic load was analyzed. Rabiee and Galehdari8analyzed the vibration of composite helicopter rotor blades, but the blade section components were relatively simple. The above analysis methods and results lay a foundation for the practical application of composite materials on hingeless rotors.
In view of the above,to improve the efficiency of composite blade structure design, a fast structure generation method based on parametric description of blade section components was established.Based on the finite element theory,the method can obtain the profile characteristics of blades efficiently and accurately.At the same time,to get the cross-section structure design scheme of the target cross-section characteristics quickly,an inverse design method of cross-section components based on radial basis function is proposed, which realized the synchronization of the composite blade parametric design and finite element analysis of structural characteristics, and provides the necessary conditions for the dynamic optimization of the blade structure design. On this basis, a more refined aeroelastic stability analysis method for composite rotors is proposed, and applied to the aeroelastic stability analysis of rotors.The parametric effects of composite cross-section components on the aeroelastic characteristics of hingeless rotor parameters are obtained.
2. Numerical methodology
2.1. Parametric modeling and analysis method for composite blade section
2.1.1. Parameterized description of section components
C-beam composite blades usually composed of leading edge,counterweight, C-beam, skin, Z-beam, trailing edge and filled foam.According to the structural characteristics of the components, these can be divided into two categories: laminated and non-laminated. Both types of components require positioning parameters to determine their position in the cross-section,and their specific classification and functions are shown in Table 1.
After the definition of geometric structure is completed,the material library of cross section components is established.The material numbers are assigned to different materials,and the material numbers are bound to the descriptive parameters of corresponding components.The blade section of a typical C-beam configuration is illustrated in Fig. 1,which shows the parameter description of the different componentsX,Yis the vertex coordinates. Among them, all positioning parameters use chord length as dimensionless standard.
2.1.2. Modeling and grid generation of sectional components
Laminated structures include leading edge, skin and Z-beam.Leading edge is generally isotropic metal material, while skin and Z-beam are generally made of composite layers. Therefore, its parameters include the number of composite layers,the thickness of single layer and the ply angle. The structural model is based on the equal distance generation method,9and the basic idea is shown in Fig. 2.
TheApoint is the point to be offset,BandCare adjacent points, nAA′is the sum of nABandnAC, β is the grid angle and the position ofA′is given by the Eq. (1):
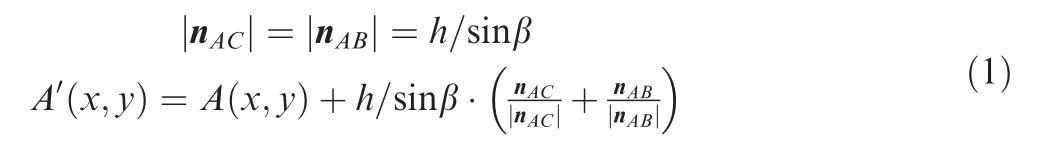

Table 1 Classification and function of blade cross section components.
wherehis the thickness of layer.
The mapping method10is used to generate the grids for laminated structure.The basic idea is to divide complex region into eight-node quadrilateral blocks, and isoparametric mapping is used to generate grids within each block. In the grid generation of laminate components, due to the components have multi-layers, and the material characteristics, thickness and ply angle of different layers can be different, the grid elements in the whole layer can be given the same number of layers by partitioning and generating block grids according to the layers, which reduces the modeling difficulty of composite components. Fig. 3 gives a sketch of layered plate structure grid based on mapping method.Combining CST(Class Shape Transformation) method, quadrilateral grid of high quality can be generated.
Non-laminated structures mainly include C-beam,counterweight,foam filling and trailing edge.Generally,shape control points are needed to describe the parameters.Because the density and stiffness of the foam filled in the blade are lower than those of other materials, it is mainly used to maintain the shape of the blade. The positioning parameters of C-beam are determined based on the algorithm of constant area.9In the parametric description of C-beam, the cross-section area is taken as input constraint, and the shape is adjusted on the basis of unchanged cross-section area. The diagram of area adjustment is given in Fig. 4,X,Yis the vertex coordinates,CandBare design points before optimization,dis the optimization point.

Fig. 1 Parameter description of typical C-beam section components.

Fig. 2 Equal distance generation method for laminated structure.

Fig. 3 Mapping method-based generation of layered plate structural grids.
Triangular unstructured grids have better filling ability,and are adopted for non-laminated structures because of its complex shape. The Delaunay triangulation method11is used to generate grids. After obtaining the shape of non-laminated structure, the input file of the triangle grid edited software12is generated, and then the triangle program interface is invoked to realize the automatic generation of grids. Fig. 5 shows the C-beam component grid generated by this program.It can be seen that this method can generate high-quality unstructured grids.
In addition, to ensure the accuracy of finite element analysis, the interface grids between laminated and non-laminated structures should be aligned, as shown in Fig. 6.
2.1.3. Flow chart for analysis of structural characteristics of rotor blade section
In this paper,VABS program is used to analyze the structural characteristics. VABS is a cross-section finite element analysis program based on the principle of gradual variation proposed by Hodegs and Cesnik13It is widely used in the analysis of rotor cross-section characteristics.It can calculate the stiffness,mass matrixes, and the position of center of gravity. Fig. 7 shows the flow chart of parametric modeling and section analysis of blade cross section.
2.2. Rotor structure analysis model
2.2.1. One-dimensional beam analysis model
YF beam element model4with 23 degrees of freedom is used,in which the end nodes of each element have 9 degrees of freedom, i.e.v,vx,w,wx, φ,u, α, γxηand γxζ; the middle nodes of each element have 5 degrees of freedom,i.e.φ,u,α,γxηand γxζ.The node degrees of freedom of blade beam unit are shown in the Fig. 8.
Its strain relationship is:

wherex1denotes the axial location of the cross-section andx2,x3are orthogonal tox1.In Eqs.(2)-(4),the 1D axial and shear strain measures at the reference line,which are functions of thex1coordinate only, are given by γ11, γ12, and γ13, respectively.The initial twist is denoted byk1. The out-of-plane warping displacementsw1are functions ofx1,x2, andx3.
The constitutive relation is assumed to be uniaxial stress,i.e. ignoring in-plane stress, as shown in the Eq. (5):

Fig. 4 Schematic diagram of automatic adjustment algorithm for C-beam with constant area.

Fig. 5 Generation of C-beam grids by Delaunay method.

Fig. 6 Interfacial grids processing of laminated and nonlaminated structures.

Fig.7 Parametric modeling and structural analysis flow of blade section.

Fig. 8 Schematic diagram of blade structure calculation model.

where σ and γ are stress and strain,Q is the stiffness coefficient.To obtain the required cross-section characteristic constants in the beam element model, Eqs. (6)-(8) is substituted into the cross-section strain energy expression of YF model beam,and the cross-section characteristic constants are obtained

where H.O.T.refers to higher order terms which are present in the VABS formulation but are not accounted for in the YF strain relations,U1is a linear term of strain energy andU2is a non-linear term of strain energy:

For the linear strain energyU1, Y is a 9×9 symmetric matrix containing integrals over the cross-section. The elements of Y are needed as inputs for the YF model, and are computed by the 2D finite element cross-sectional analysis described in Kosmatka.14K obtained from the twodimensional section analysis one by one. For the nonlinear strain energy part,because the two-dimensional section analysis in this paper is based on the linear theory, it is unable to provide the coefficient inU2, so other parameters exceptY17are set to 0 in the specific implementation,and forY17,the values are as follows:

This item reflects trapezoid effect, representing high-order pull-up torsional coupling, which is particularly important for the helicopter rotor working in the centrifugal force field.
2.2.2. Stability analysis model
By using Hamilton’s principle,15a set of partial differential equations describing the rotor motion is derived. The beam element with 23 degrees of freedom of the YF model is used for spatial discretization. Finally, a set of time-varying nonlinear ordinary differential equations is obtained, as follows:

where M, C and K are the mass, damping and stiffness matrixes of non-linear system. F is the external force vector.q is the degree of freedom The Newmark-beta method16,17is used to solve the steady-state periodic response. On the basis of the solution of the steady-state periodic response, the Eq.(9) is linearized and the results are as follows:


where ψ is the azimuth. Because the matrix A of the system is periodic,the state transition matrix φ(2π,0),on a period must be solved first. Then the eigenvalue analysis of the matrix is carried out to obtain the eigenvalue multiplier Λj=Zj±iΩj,and the eigenvalue exponent lambda λj=ςj±iωj. The real part ςjand the imaginary part ωjcan be calculated by the following Eq. (13):

where τ=2π. The real part of the eigenvalue represents the damping of a certain mode, and the rotor is aeroelastic stable when there is ς<0 for allj.
2.2.3. Aerodynamic model of blade section

where ρAis the air density,ais the two-dimensional airfoil lift curve slope;bis the semi-chord,XAis the blade airfoil crosssectional aerodynamic center offset from the elastic axis, positive for aerodynamic center before elastic axis.

Fig. 9 Schematic diagram of airfoil aerodynamic model.
The detailed calculation steps are as follows:
(1) A one-dimensional beam structure analysis model is constructed and its modal analysis is carried out to obtain some low-order modes for conversion from physical space to modal space.
(2) The initial response of the blade motion is obtained by solving the linear system with respect to stiffness and generalized force, and then the deformation of the first periodic blade is calculated by Newmark-beta method.
(3) Considering the aerodynamic model of an elastic rotor and updating the local induced velocity of the blade,the induced velocity is used to calculate the blade deformation in the next cycle.
(4) Newton-Raphson method is used to update the balancing control quantity. If the manipulation does not converge, step (3) is executed to recalculate the next cycle,otherwise, the steady-state periodic response is used as input for aeroelastic stability analysis.
2.3. Inverse design method for section components
By combining genetic algorithm with surrogate model,an efficient combinatorial inverse design method is established. The key point of this method is to generate sample points and construct approximate model, i.e. experimental design method and approximate method.
2.3.1. Experimental design method
The experimental design method determines the total number and spatial distribution of the initial sample points.If the spatial distribution of sample points is reasonable, even if a small number of sample points is used, better prediction accuracy will be obtained.20In this paper, the improved Latin hypercube method is adopted as the experimental design method.The traditional Latin Hypercube Sampling(LHS)method generates sample points randomly,which is prone to the improper local density. Some scholars proposed to take the maximum average distance between sample points as the optimization objective (s-optimization), and use genetic algorithm to optimize the traditional Latin hypercube method. The sample points generated by this method are more uniform than the original method. Therefore, this paper uses the genetic LHS method21as the experimental design method.
Fig.10 shows the sample point distribution of random LHS experimental design and genetic LHS experimental design method for 100 sample points of 2 variables. It can be found from the graph that the sample points generated by genetic LHS method are more evenly distributed in the whole space than those generated by traditional random LHS method.
2.3.2. Approximate method
Radial Basis Function(RBF)22is used to fit the response value of data space. Gaussian function is selected as the basis function, and its form is as follows:

In Eq. (18),r=‖X-Xi‖ is Euclidean norm, and σ is adjusting parameter. Changing its value can adjust the fitting accuracy of the model. Fig. 11 shows the full optimization procedure.
3. Result analysis
3.1. Modular validation
3.1.1. Verification of rotor dynamics
The structure analysis model is validated through analyzing the natural frequency of UH-60A rotor.23F,L and T represent the flapping, lagging and torsion modes in Fig. 12. The reference results are calculated using UMARC software,24and the discrepancies between the calculated and reference results are minor.
3.1.2. Verification of aeroelastic characteristics of rotor blades
The blade configuration has fundamental rotating frequencies of 1.15/rev,1.5/rev and 5.0/rev in flap,lag and torsion,respectively. The data for the baseline configuration of the blade is taken from Ref.25. Results from the present analysis are compared with those obtained in Fig. 13. It is evident that the results of the present analysis show an excellent correlation in the lag, flap and torsion modes with those obtained in Ref.25.
The results of the stability analysis are shown in Fig. 14.Fig.14(a)presents the variation of modal frequency as a function of collective pitch of the blade; while the variation in modal damping as a function of collective pitch angle is shown in Fig. 14(b). The results corresponding to the present study provide an excellent correlation in modal frequency and very good correlation in modal damping with the results of Ref.25.
To validate the forward flight analysis, a correlation study with another different model, developed in Ref. 25 was conducted. Careful comparisons for blade aeroelastic response were carried out. The flap, lag and torsional tip deflections of the blade at an advance ratio of μ = 0.3 are compared in Fig.15 for the blade configuration.The correlation is excellent for the flap and lag modes. There is a mild discrepancy in the torsional tip deflection compared with Millott ans Friedmann,26which can be attributed to the differences in the treatment of the axial degree of freedom, which influenced the torsional frequency slightly.
3.2. Inverse design method results for section components
To analyze the aeroelastic stability of composite rotor, the rotor in Ref.25is selected as an example to study which is shown in Fig. 16.Cis chord length andRis blade radius.The aerodynamic shape of the blade is consistent with the blade in Ref. 25.
The internal structure of the rotor is designed by using MH104 airfoil. The configuration scheme of internal components is unknown,which is obtained by inverse design method analysis. Based on the parameterized modeling method of composite blade section established above, the section structure design template and the corresponding finite element grids discrete schematic diagram of the blade are given in Fig. 17.The ply angle of blade skin and Z-beam are ±45°.
The formwork includes blade leading edge, skin, C-beam,Z-beam and trailing edge. Since honeycomb is only used to maintain blade cross-section shape, the influence of its mass and stiffness characteristics on the overall cross-section characteristics can be neglected. Detailed material properties are shown in Table 2. The counterweight is temporarily cancelled in this example.



Fig. 10 Sample point distribution diagram of different experimental design method.

Fig. 11 Optimization procedure.

Fig. 12 Resonance diagram of UH-60A rotor blade.

Fig.13 Tip response in hovering as a function of blade collective pitch.
The thickness and position parameters of the leading edge are given in Table 4.
At the same time, to avoid failures of the cross-section parametric modeling program, it is necessary to constrain the optimization variables of cross-section structural parameters and avoid non-physical results such as structural collision.
Definition δ = 0.01C, representing the minimum spacing between adjacent cross-section components. The position parameters of the blade section assembly are constrained as follows.


Fig. 14 Stability analysis of blades in hovering as a function of blade collective pitch.

Fig. 15 Blade tip response at μ = 0.3.

Fig. 16 Model rotor blade planform.
The objective function of the design of the blade structure is the natural frequency of the blade, which can be expressed as:

ωciand ωtiare the calculated and objective values of the first natural frequencies, respectively. In this paper, the first order natural frequencies of flapping, lagging and torsion are selected as design objectives.
Fig. 18 shows the initial sample points obtained by the genetic LHS experimental design method.The number of variables is 9, the number of sample points is 750, the number of effective sample points satisfying the constraints is 196.To display conveniently, three-dimensional sketches of sample space are given.
After obtaining the sample points, the section analysis model established is used to calculate the ‘‘response value”,including the linear density of the section and the flapping,lagging and torsional stiffness. Then the approximate model is constructed by using Radial Basis Function (RBF).
The objective function of genetic algorithm changes as shown in Fig. 19. It can be seen from the graph that after about 20 generations,the population tends to be stable.Specific structural optimization variables are shown in Table 5.
Comparing the natural frequencies of blades with those of original in Table 6, it can be seen that the errors of first flap and first lag frequencies exceed 5%, but remain within 8%,while the errors of first torsion natural frequencies are within 3%, which is in good agreement with the original blades,which shows that this method has achieved the design objectives of this section.
3.3.Parameter influencing analysis of aeroelastic characteristics of rotor
3.3.1. Effects of structural layers
First, the aeroelastic stability analysis of the rotor system in hover withCT=0.0025,CTis the thrust coefficient of rotor.The influence of cross-section ply angle and Z beam on rotor dynamic characteristics is studied. The design is divided into six cases: 2 layers with Z beam, 4 layers with Z beam, 6 layers with Z beam, 2 layers without Z beam, 4 layers without Z beam and 6 layers without Z beam. The adjacent two layers are orthogonal, and each pair of layers is a group of cyclic layouts.

Fig. 17 Drawing of section components of C-beam of MH104 airfoil.

Table 2 Material properties.
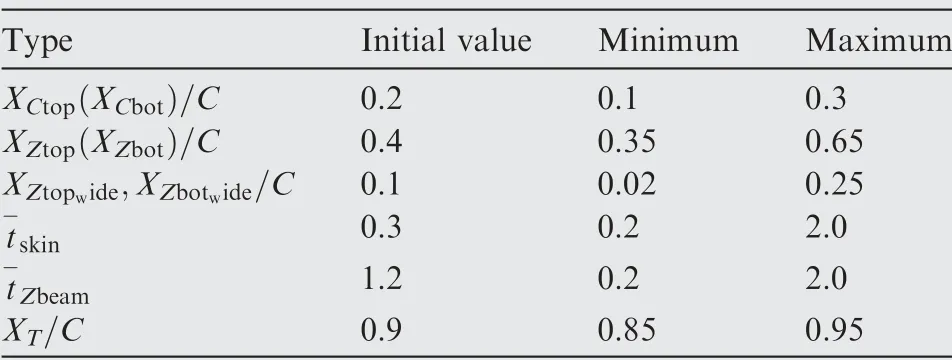
Table 3 Initial values and allowable ranges of structural design variables for blade section.

Table 4 Laminate structural parameters.

Fig. 18 Sample point distribution (9 Variables).

Fig. 19 Composite blade structure design target value varies with evolutionary algebra.

Table 5 Structural design parameters of composite blade design variable.

Table 6 Frequencies comparison.

Fig. 20 Root locus of first torsion mode eigenvalues as a function of ply angle.

Fig.21 Root locus of first lag mode eigenvalues as a function of ply angle.
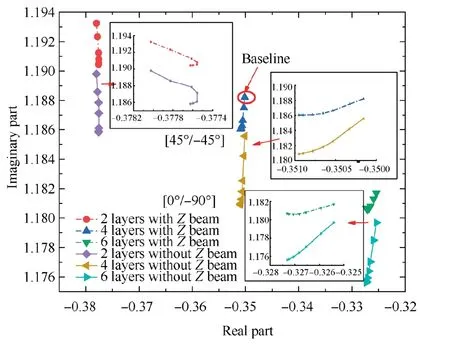
Fig.22 Root locus of first flap mode eigenvalues as a function of ply angle.
It can be seen from Fig.20 that the torsion damping of the[45°/-45°] angle layer is the maximum and [0°/-90°] is the minimum in all cases,except that case 4 has a minimum damping of-0.132 when laminated at[15°/-75°].However,under thrust coefficient ofCT=0.0025, the torsion margin is large enough, and the aeroelastic instability phenomenon does not occur. In addition, the Z-beam can also effectively increase the torsional damping and reduce the influence of the ply angle on the damping.It can be seen that in the absence of a Z-beam,the variation of the case 4,5,and 6 ply angles results in a large variation in torsional damping,where the torsional damping of case 5 varies from -0.14 to -0.258, and the relative change range is close to 81.6%. The change range of torsional damping of case 1 to case 3 is relatively small considering Z-beam.In addition, the increase in the number of layers can reduce the influence of the ply angle on damping, but it can also reduce the torsional damping.In the case of the Z-beam,case1 is only two layers, and the variation of the ply angle lead to the change range of torsional damping close to 0.04 (from -0.23 to -0.27), while the change of torsional damping with the change of ply angle is only about 0.01 (from -0.23 to -0.24)with six layers of case 3. Increasing the number of layers and adding Z-beams can increase the first torsional frequency.The first torsion frequency of each case varies with the ply angle of the layers on average.It can be seen that the thickness of the skin,the direction of the layers and Z-beams have great influence on the stability of the torsion mode.
Fig.21 shows that,unlike the root locus first torsion mode,the first lag stability of each case is the strongest stability of each case is the strongest at the ply angle of [0°/-90°], while the weakest is at ply angle of [45°/-45°]. The absolute variation ranges from 0.005 to 0.008. In addition, Z-beam and increasing the thickness of layer will also reduce the lag stability.It can also be seen from the figure that although each case is aeroelastic stable, the lag stability margin is small. In the dynamic design of composite rotor, attention should be paid to the range of components to avoid the aeroelastic instability.

Fig. 23 Natural frequencies as a function of ply angle.

Fig. 24 The 4/rev vibratory hub shear.
Fig.22 shows the results of the first flap stability analysis.It can be seen from the figure that the first order mode has a large stability margin,which may be due to the aerodynamic damping of the flap degree of freedom. The influence of the change of the ply angle and the Z-beam on the stability of the first flap mode is very small, and the variation range is less than 0.001.However,the thickness of the layer has a great influence on the flap damping. The absolute flap damping decreases by about 0.025 with an average increase of two layers.
From Fig. 23, it can be seen that:
1. The Z beam can reduce the first torsional frequency and increase the first flapping and lagging frequencies.The main reason is that the Z-beam has little influence on torsional stiffness, but increases the sectional density, which leads to the decrease of torsional frequency.
2. The torsional frequency increases monotonously with the ply angle in the range of 0°to 45°of the first layer, and the influence is the greatest, with the average range of change from 0.4 to 0.8. The flapping and lag frequencies decrease monotonously with the ply angle,but in fact,they have little influence on the first order flap frequency. The average variation range is only about 0.002, and the first order lag frequency range is about 0.04 to 0.1.
3. Increasing the thickness of skin can increase the first torsion frequency and decrease the first flap frequency.The average value of 1T and 1F can be increased by about 0.3 and 0.005 for each layer.However,the influence of layer thickness on 1L is more complex. As can be seen from Figure b, when the angle of the first layer is 0°, the thickness of the layer has little effect on 1L. However, with the increase of the angle of the first layer, the influence of the thickness of the layer on 1L becomes larger gradually. When the angle of the first layer is 45°, the 1L decreases by about 0.03 per two layers on average.

Fig. 25 Schematic diagram of C-beam shape changing with area.
Fig. 24 calculates the 4/rev vibratory hub shears of a forward flight at an advance ratio of 0.30. The vibratory hub shears are obtained from the integration of the distributed inertial and aerodynamic loads over the entire blade span in the rotating frame. Subsequently, the loads are transformed to the hub-fixed non-rotating system, and the contributions from the individual blades are combined25. From Figs. 24(a),(b),(c),it can be seen that the longitudinal force and lateral force change regularly. With the increase of the first skin ply angle,the longitudinal and lateral hub loads can be effectively reduced by 0.01 to 0.02 (dimensionless value). At the same time, increasing the thickness of the layer can also reduce the hub loads.The effect of increasing from two layers to four layers is more obvious, while the effect of increasing from four layers to six layers is weaker. However, the longitudinal load will increase without Z beam. It can be seen from Figs. 24(c) that the variation of vertical load is more complex. It can be seen that the ply angle, layer thickness and Z-beam are important to the hub loads, and the case 3[45°/-45°] can effectively reduce the hub loads.
3.3.2. Effects of the C beam
The influence of the area change of the C-beam on the dynamic characteristics of the rotor was studied. KeepingXCmid=0.097C,XCtop=XCbot=0.233Cconstant, the Cbeam area varies fromSCbeam=0.1SstoSCbeam=0.2Ss, and other cross-section components such as blade ply angle and Z-beam position are reference values, as shown in Figs. 25(a)to (f).
The root locus of first lag,flap and torsion mode are shown in the Fig.26.With the increase of the area of the C-beam,the first lag and flap stability will decrease,while the torsion stability will increase. However, the stability margins of both flap and torsional modes are large,and there will be no aeroelastic instability.Although the area of C-beam has the smallest influence on the lag stability, the margin is very small, and continuous increase of the area of C-beam may lead to aeroelastic instability.
Fig.27 shows 4/rev vibratory hub shears and moments as a function of the parametersSCbeam. The variation in vertical shears is about 55% from the minimum configuration, while the longitudinal and lateral shear is less sensitive to the variation inSCbeam.The roll and pitch moments decrease withSCbeamup to about 20%relative to the minimum.The maximum variation in yaw moment consists of an increase of 7.57%.

Fig.26 Root locus of first mode eigenvalues as a function of Cbeam’s area.

Fig. 27 Vibratory hubloads as a function of C-beam’s area.
4. Conclusions
Focused on typical composite blade with C-beam configuration,this paper presented a method for modeling and finite element analysis of composite blades. The cross-section part in the entire model was divided into laminate part and nonlaminate part and parameterized by introducing thickness,geometric position and design control points. Then the input file of VABS was generated,by which the cross-section characteristics of the blade were calculated. To obtain the target cross-section characteristics, an inverse design method based on RBF was developed. By virtue of the dynamic analysis of a YF medium deformable beam model, a set of structural designs of composite rotors were performed. Based on that,the aeroelastic characteristics of the composite hingeless rotors were studied with respect to the cross-sectional parameters.The results shown that:
(1) For composite blades in C-beam manner,the parametric modeling method of blade cross-section here can quickly generate blades with different geometric shapes and cross-sectional components, and the entire model possesses high efficiency and robustness.
(2) The proxy model based on Latin hypercube experimental design and radial basis functions, which is combined with a genetic algorithm, can reduce the amount of calculation significantly with consideration of the calculation accuracy. It also realizes the inverse design of cross-section components for complex non-linear issues.
(3) The ply angle in the composite blade has great influence on the first-order torsion and lagging stability, but has little effect on the first-order flapping stability. It is demonstrated that adding the Z-beam can improve the first-order torsional stability and reduce the first-order lagging stability,but it also has no effect on the flapping stability. Flapping, lagging and torsional stabilities are sensitive to skin thickness and C-beam area.In addition,the sensitivity of first-order torsional damping to ply angle and skin thickness can be generally reduced by adding z-beam. The first-order lagging stability margin is small,so special attention should be paid to the design of composite blades.
(4) It is shown that increasing the skin thickness, adding a general Z-beam and changing the angle of ply angle can reduce the hubloads effectively. Especially when the area of C-beam is about 16%, the entire structure has better load performance.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Tangling and instability effect analysis of initial in-plane/out-of-plane angles on electrodynamic tether deployment under gravity gradient
- Aerodynamic periodicity of transient aerodynamic forces of flexible plunging airfoils
- Effects of swirl brake axial arrangement on the leakage performance and rotor stability of labyrinth seals
- Experimental and computational investigation of hybrid formation flight for aerodynamic gain at transonic speed
- Tomography-like flow visualization of a hypersonic inward-turning inlet
- Hypersonic reentry trajectory planning by using hybrid fractional-order particle swarm optimization and gravitational search algorithm
