Effects of swirl brake axial arrangement on the leakage performance and rotor stability of labyrinth seals
2021-03-16YoxingCHENZhigngLIJunLIXinYAN
Yoxing CHEN, Zhigng LI, Jun LI,b,*, Xin YAN
a Institute of Turbomachinery, Xi’an Jiaotong University, Xi’an 710049, China
b Collaborative Innovation Center of Advanced Aero-Engine, Beijing 100083, China
KEYWORDS Circumferential velocity;Labyrinth seal;Leakage;Numerical analysis;Rotor stability;Swirl brake
Abstract Swirl brakes are usually introduced at the seal entrance in industry to improve the seal stability, especially for labyrinth seals suffering low seal clearance and high inlet preswirl ratio.However, how to arrange swirl brakes at the seal entrance to obtain better seal stability retains unknown, such as the axial distance between the brake trailing edge and the first tooth. To this end,the effects of the distance between brakes and the first tooth on the leakage flow rate and seal rotordynamic coefficients were numerically investigated at typical inlet preswirl ratios of 0.45 and 0.8, and the predicted results were in comparison with the results for no-brake configuration. The obtained results disclose that the brake configuration arranged against the first tooth produces lower circumferential velocity in the downstream of the brakes as a result of the larger counterclockwise vortex moving from the brake trailing edge to the brake leading edge when compared to the brake configuration away from the first tooth. Besides, the dropped circumferential velocity in the downstream of brakes will cause larger pressure fluctuation in the circumferential direction and thus generates larger tangential force to restrain the rotor forward whirl. On the other hand,the effective damping is further increased when the distance between brakes and the first tooth decreases to zero, that is, the crossover frequency is even disappeared at the inlet preswirl ratio of 0.45 and successfully drops from 69.9 Hz to 32.7 Hz at the preswirl ratio of 0.8.
1. Introduction
Labyrinth seals are widely used in modern gas turbines and centrifugal compressors for their reliability, simplicity as well as their forgiveness when radial misalignment of the rotor and casing centerlines occurs.1Their primary task is to restrict the leakage through rotor-stator clearances. However, instability becomes a common concern for labyrinth seals when lower rotor-stator clearances are adopted to pursue higher efficiency and power output of gas turbines and centrifugal compressors in recent years.2On the other hand, the centrifugal growth under high rotational speed3and thermal expansion under high temperature4for labyrinth seals will also contribute to a lower clearance and may provoke instability at a system level. Usually, there are two approaches to deal with these instability issues. One is to replace the unstable labyrinth seals with stable and reliable damper seals, such as honeycomb seals,5hole-pattern seals6and pocket damper seals.7The other is to introduce swirl brakes at the seal entrance to impede the strong circumferential flow of the fluid.8Childs et al.9pointed out that introducing swirl brakes in the turbine interstage seal could completely eliminate the subsynchronous vibration problems in the Space Shuttle Main Engine High Pressure Oxygen Turbopump over the full steady-state range.
In the open literature,some investigations on the rotor stability of labyrinth seals with swirl brakes have been conducted.Nielsen et al.10made a comparison between non-aerodynamic swirl brakes and aerodynamic swirl brakes in terms of crosscoupling stiffness and seal inlet preswirl ratio.They found that aerodynamic swirl brakes can obtain a better stability performance at high rotational speed and high inlet swirl ratio.Iwatsubo and Iwasaki11introduced swirl brakes at seal cavities and investigated the effects of the number and the location of swirl brakes on the circumferential velocity and dynamic fluid forces,and they pointed out that the effects of brakes is significant when brakes are arranged at the first and second chamber. Childs et al.12experimentally investigated the leakage performance and rotor stability of labyrinth seals with three different brake configurations: no-brake configuration, conventional brake configuration and negative brake configuration. Their results showed that the negative brake configuration possesses smaller leakage and larger effective damping compared to other two brake designs. Sun et al.13implemented an experimental investigation to analyze the influence of brake number and brake length on the rotordynamic characteristic of the labyrinth seal. Untaroiu et al.14employed a novel design of experiments approach to quantify the influence of different brake geometry parameters on the seal stability. These brake geometry parameters contain brake length, brake width, brake number, brake curvature at the ends and stagger angle of the brake.
To gain a deep insight of the effect of swirl brake axial arrangement on the leakage performance and rotor stability of labyrinth seals,the effects of the distance between the brake trailing edge and the first tooth on the leakage flow rate and rotordynamic coefficients were investigated and analyzed at two typical inlet preswirl ratios of 0.45 and 0.8, and the predicted results were in comparison with the results for nobrake configuration.
2. Computational model
In this work, the seal geometrical parameters of the straightthrough labyrinth seal were chosen on the basis of the results presented by Ertas et al.15Fig.1 demonstrates the basic design for the labyrinth seal with swirl brakes. The swirl brakes were installed at the seal entrance and the brake configuration had 72 vanes at their base radius of 89.31 mm. The brake height was 3.71 mm and the brake length was 5.0 mm. The distancedbetween the brake trailing edge and the first tooth was designed to be two typical values:0 mm and 1.5 mm.Actually,the conditiond=0 mm can be achieved only when the brakes and the labyrinth are simultaneously designed and manufactured. Due to the fact that the emphasis in this work is on the swirl brake axial arrangement, the tooth number for the straight-through labyrinth seal was decreased to 6 with a consideration of reducing computational mesh. On the other hand, the vertical leading edge of the first tooth was utilized on purpose to easily adjust the distance between brakes and the first tooth from 1.5 mm to 0 mm.
Table 1 lists the detailed geometrical parameters for swirl brakes and the labyrinth seal. The operational condition for the labyrinth seal with different brake configurations is mostly based on the Ref.15and given in Table 2.Noticeably,the outlet pressure is artfully changed to be 383 kPa with an attempt to avoid the choked condition at the last tooth. The swirl ratio is defined as the ratio of the circumferential velocity of the fluid and the adjacent rotor surface velocity,and given by Eq.(1).It should be pointed out that the swirl ratio at the seal inlet is named the inlet preswirl ratio, and given by Eq. (2).

whereVis the circumferential velocity of the fluid,Vinis the circumferential velocity of the fluid at the seal inlet,D0is the seal inner diameter,nis the rotational speed of the rotor.
As introduced in Ref.16, the inlet preswirl ratio is around 0.1-0.8 for typical shaft seals, eye-packing seals and balancedrum seals, thus the maximum inlet preswirl ratio of 0.8 and the medium inlet preswirl ratio of 0.45 were chosen in this work.Fig.2 illustrates the straight-through labyrinth seal with no-brake configuration and two axial brake configurations.
Fig. 3 shows the computational model and mesh of the labyrinth seal with different brake configurations. As shown in Fig.3,the computational model consists of the inlet region,seal cavities with swirl brakes and the outlet region. The computational model was built in 360° to obtain the non-uniform circumferential flow field and the exciting force acting on the rotor, and this is the key to obtain rotordynamic coefficients by the transient solution.17The multi-block structured mesh was generated to guarantee a good mesh quality and the zoomed view was used in particular to present the adjacent mesh of brakes in the axial direction more clearly.
3. Numerical method
To investigate the influence of the axial distance between the brake trailing edge and the first tooth on the leakage performance and rotor stability of labyrinth seals, the leakage flow rate and rotordynamic coefficients of labyrinth seals with different brake configurations were obtained by solving the Unsteady Reynolds Averaged Navier-Stokes (URANS) solution based on the multi-frequency elliptical orbit rotor whirling model and dynamic mesh technique.17As stated in Ref.18, the instability induced by the seal is mainly a subsynchronous phenomenon. Hence, the fundamental frequencyf0=20 Hz combining with the frequency numberN=13 was utilized to cover the whole subsynchronous frequencies below 250 Hz.Table 3 lists the numerical method for the transient CFD solution adopted in this work. The convergence of the transient calculation is achieved when the value of the root mean square equation residuals reaches 10-5and the response forces acting on the rotor periodically oscillate with a difference less than 1% between two adjacent vibration periods.

Fig. 1 Basic design for labyrinth seal with swirl brakes.

Table 1 Geometrical parameters for swirl brakes and labyrinth seal.

Table 2 Operational condition.

Fig. 3 Computational model and mesh of labyrinth seal with different brake configurations.
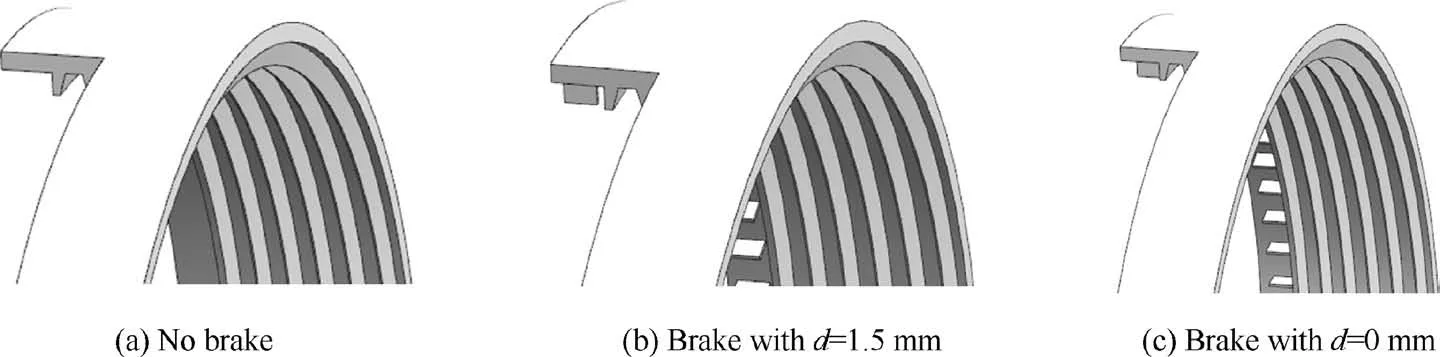
Fig. 2 Straight-through labyrinth seal with no-brake configuration and two axial brake configurations.
For a small motion around the centered position, stiffness coefficients (Kxx,Kxy,Kyx,Kyy) and damping coefficients(Cxx,Cxy,Cyx,Cyy) are commonly defined by the linear force-displacement model as illustrated in Eq. (3).

WhereFxandFyare the rotor exciting force components,DxandDyare the rotor whirling motion components.
In the transient solution, the rotor displacements (Dx,Dy)are predefined by Eq. (4) and Eq. (5). The response forces(Fx,Fy)acting on the rotor are the resultant force of integrating circumferential pressure and shear stresses.
The rotor displacements atx-direction excitation:


Table 3 Numerical method.
Then Eq.(3)can be solved and transformed into Eq.(6)to Eq. (8) withxexcitation andyexcitation in the frequency domain. For the response forceFijand the rotor displacementDij,the first subscript is the excitation direction and the second subscript is the direction of the response force or the rotor displacement. More detailed introduction about the determination of the rotordynamic coefficients can be found in Refs.17,19

The rotor stability of labyrinth seals is commonly determined by two parameters: the cross-coupling stiffness and the direct damping. The positive cross-coupling stiffness produces the destabilizing cross-coupling force in the tangential direction dragging the rotor forward whirl while the positive direct damping produces the stabilizing direct force in the tangential direction restraining the rotor forward whirl. Hence,the effective dampingCeffis usually introduced to evaluate the stability of labyrinth seals and is described as Eq. (9).

The transient solution approach for predicting rotordynamic coefficients was validated by comparing the experimental data published in Ref.15As proposed by Refs.20,21, the inlet/outlet regions were also taken into account in the estimation of rotordynamic coefficients. The test data of stiffness coefficients and damping coefficients are depicted in Fig. 4,where two predicted results considering the inlet/outlet regions or not are also plotted. As illustrated in Fig. 4, compared to the predicted results without inlet/outlet regions,the predicted results with inlet/outlet regions reach a better agreement with the experimental data, indicating that the inlet/outlet regions make an important contribution on the rotordynamic coefficients, especially for the direct stiffness. For the predicted results with inlet/outlet regions, the direct stiffness is in good accordance with the experimental data, whereas the direct damping is obviously under-predicted,especially at frequencies below 120 Hz. On the other hand, the cross-coupling stiffness and the effective damping are modestly well-predicted at frequencies below 160 Hz. The prediction errors are resulting from the difference in the velocity distribution adopted at the seal entrance between the CFD and the experiments,which has also been reported in Ref.22In general, the transient solution approach has reasonable accuracy in terms of predicting rotordyamic coefficients of labyrinth seals and can be used for further studies.
To demonstrate that the numerical results are not sensitive to the mesh density, three different meshes with 3.56 million nodes for coarse mesh, 6.13 million nodes for medium mesh and 8.69 million nodes for fine mesh were generated and calculated for the brake configuration withd=0 mm at inlet preswirl ratio of 0.45. The mesh independence was firstly evaluated by the leakage flow rate. As shown in Fig. 5(a),the leakage flow rate increases by 0.8% when the grid nodes increase from 3.56 million to 8.69 million, that is, the leakage flow rate is actually independent of the grid nodes even though the coarse mesh is adopted in this work.As shown in Fig.5(b),the mesh independence was then evaluated by the direct damping and the cross-coupling stiffness. At frequencies below 200 Hz, the cross-coupling stiffness differs less than 12.9%between the medium mesh and the fine mesh while the crosscoupling stiffness differs up to 32.0%between the coarse mesh and the fine mesh. At frequencies above 200 Hz, the crosscoupling stiffness slightly decreases with the grid nodes. On the other hand, the direct damping increases by 3.0%-7.6%when the grid nodes increase from 3.56 million to 6.13 million,and increases less than 2.5%when the grid nodes keep increasing. Therefore, as a tradeoff of the computation time and the accuracy,the final mesh size for the labyrinth seal with brakes in this work was chosen as 6.13 million nodes.
4. Results and discussion
4.1. Leakage flow rate
Fig.6 illustrates the leakage flow rate versus inlet preswirl ratio for no-brake configuration and two axial brake configurations.For the no-brake configuration, the leakage flow rate through the labyrinth seal decreases by 6.09% when the imposed inlet preswirl ratio varies from 0.45 to 0.8. For the inlet preswirl ratio of 0.45, the leakage flow rate through the labyrinth seal decreases(decrease by 1.66%for the brake configuration withd=1.5 mm and decrease by 1.94% for the brake configuration withd=0 mm) when swirl brakes are introduced at the seal entrance.This is attributed to the strengthened eddy dissipation induced by a series of brakes in the circumferential direction. Besides, a decrease of 1.84% for the brake configuration withd=1.5 mm and a decrease of 2.66%for the brake configuration withd=0 mm are observed in the leakage when the inlet preswirl ratio is elevated to 0.8.
4.2. Circumferential velocity
Fig. 7 shows the mean circumferential velocity versus axial position at seal cavities and vane-to-vane flow field at the middle radial span position. As shown in the Fig. 7, the no-brake configuration produces the maximum circumferential velocity among three brake configurations,irrespective of inlet preswirl ratio.When swirl brakes are arranged at the seal entrance,the circumferential velocity is effectively impeded by the brakes and begins to fall rapidly along the axial direction and reaches a minimum value at the trailing edge of the brakes, and then grows gradually as a result of the viscous friction effect of rotating surfaces. As expected, the brake configuration withd=0 mm has an obvious advantage in weakening the circumferential velocity compared to that withd=1.5 mm,and even some surprising negative circumferential velocity in the downstream of swirl brakes is discovered in the brake configuration withd=0 mm, which can be explained by the vane-to-vane flow filed.

Fig. 4 Rotordynamic coefficients vs whirling frequency at inlet preswirl ratio of 0.45.

Fig. 5 Mesh density study for brake configuration with d=0 mm.

Fig. 6 Leakage flow rate vs inlet preswirl ratio.
As shown in the right of Fig.7,the upstream flow with high preswirl velocity impinges on the Pressure Side (PS) and flows against the pressure side to the Trailing Edge (TE). At that time, for the brake configuration withd=1.5 mm, the flow at the trailing edge is divided into two part: one flows along the rotational direction via the gap between the brake trailing edge and the first tooth, the other flows in the opposite direction of the rotation and creates a counter-clockwise vortex moving backward from the trailing edge to the leading edge.On the other hand, for the brake configuration withd=0 mm, the flow in the direction of rotation at the trailing edge disappears as a fact that the trailing edge is arranged against the first tooth,thus the counter-clockwise vortex moving from the trailing edge to the leading edge dominates the whole vane-to-vane flow and produces lower circumferential velocity around the first tooth compared to the brake configuration withd=1.5 mm.

Fig. 7 Mean circumferential velocity vs axial position at seal cavities and vane-to-vane flow field at middle radial span position.
4.3. Stiffness coefficients
brake configurations. When the brake configuration is installed at the seal entrance, the destabilizing cross-coupling stiffnessKxyfor the brake configuration withd=1.5 mm drops by 51.4%-72.0% at the inlet preswirl ratio of 0.45 and 43.0%-53.7% at the inlet preswirl ratio of 0.8 individually,and the destabilizing cross-coupling stiffnessKxyfor the brake configuration withd=0 mm drops by 64.6%-96.8% at the inlet preswirl ratio of 0.45 and 61.5%-72.5% at the inlet preswirl ratio of 0.8.
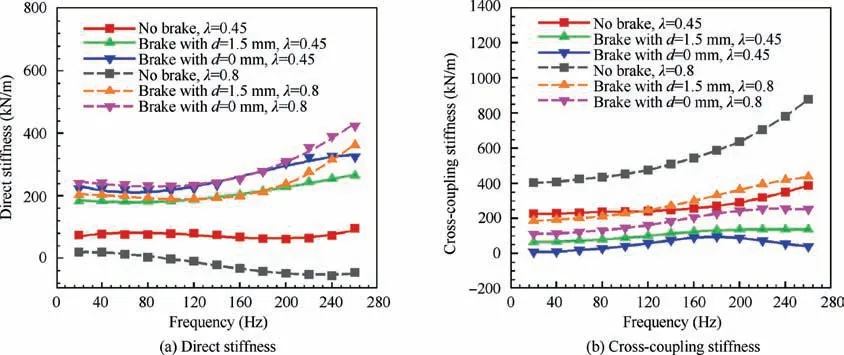
Fig. 8 Stiffness coefficients vs whirling frequency at two typical inlet preswirl ratios.
4.4. Damping coefficients
Fig.9 shows damping coefficients versus whirling frequency at two typical inlet preswirl ratios for no-brake configuration and two axial brake configurations. As shown in the Fig. 9(a), at frequencies below 200 Hz, the direct damping drops less than 15% at the inlet preswirl ratio of 0.45 and drops less than 7.4% at the inlet preswirl ratio of 0.8 when swirl brakes are arranged at the seal entrance, and there is a minor difference in the direct damping between two axial brake configurations.At frequencies above 200 Hz, the descending order in the direct damping is the no-brake configuration,the brake configuration withd=1.5 mm and the brake configuration withd=0 mm, irrespective of the inlet preswirl ratio. As shown in the Fig. 9(b), in terms of the no-brake configuration, the effective damping crosses over to negative values at frequencies below 89.8 Hz and inlet preswirl ratio of 0.45,and this implies that the labyrinth seal may suffer instability for that the net tangential force acting on the rotor is in the direction with the rotor whirl. In addition, the crossover frequency increases to 154.2 Hz when the inlet preswirl ratio of 0.8 is imposed on the no-brake configuration. When the brake configuration withd=1.5 mm is introduced at the seal entrance, the remarkably dropped cross-coupling stiffness and slightly weakened direct damping ultimately cause an increase in the effective damping compared to the no-brake configuration,meanwhile, the crossover frequency drops from 89.8 Hz to 32.5 Hz at the inlet preswirl ratio of 0.45 and drops from 154.2 Hz to 69.9 Hz at the inlet preswirl ratio of 0.8. Another important finding is that the effective damping is further increased when the distance between brakes and the first tooth decreases from 1.5 mm to 0 mm, that is, the crossover frequency is even disappeared at the inlet preswirl ratio of 0.45 and successfully drops from 69.9 Hz to 32.7 Hz at the preswirl ratio of 0.8.
4.5. Static pressure contours and response forces
Fig. 10 shows the locations of the brake region and the cavity region and two representative cross-sections. To present the response forces acting on different parts of the rotor, the seal cavities are divided into two regions at the leading edge of the first tooth:the brake region and the cavity region.Besides,the Cross-section 1 is located at the middle of the brake region for no-brake configuration or the middle of brakes for two axial brake configurations, the Cross-section 2 is located at the middle of the third cavity in the cavity region for three brake configurations.

Fig. 9 Damping coefficients vs whirling frequency at two typical inlet preswirl ratios.

Fig. 10 Locations of brake region and cavity region and two representative cross-sections.
Fig.11 shows static pressure contours of two representative cross-sections and response forces acting on the different parts of the rotor at inlet preswirl ratio of 0.8 when the rotor is whirling atxexcitation andt=0.1 s. At this special moment, the rotor is whirling to pointClocated atxdirection and its whirling velocity is tangent to the rotor motion during the elliptical whirling orbit. Noticeably, the response force F acting on the rotor has been decomposed into the radial force Frand the tangential force Ft.
As shown in the left of Fig.11,a larger pressure fluctuation in the circumferential direction resulting from the decreased cavity volume is observed when brakes are introduced at the seal entrance, and this will lead to an increased response force acting on the brake region of the rotor.On the other hand,the dropped circumferential velocity cause a slight increase in the phase angle of the response force and this will increase the radial component and weaken the tangential component in terms of the response force. Therefore, as a overall result of the pressure fluctuation and the phase angle of the response force, the radial force acting on the brake region of the rotor for brake configurations opposes to the rotor motion and is obviously strengthened in the magnitude in comparison with no-brake configuration, and this implies that the centering ability of the brake region of the rotor is remarkably enhanced when introducing swirl brakes at the seal entrance.Besides,the tangential forces acting on the brake region of the rotor for the brake configuration withd=1.5 mm and the brake configuration withd=0 mm are respectively 0.96 and 1.07 times that for no-brake configuration,indicating that the tangential force acting on the brake region of the rotor is hardly influenced by swirl brakes.

Fig. 11 Static pressure contours of two representative cross-sections (left: Cross-section 1; right: Cross-section 2) and response forces acting on the rotor (left: rotor of brake region; right: rotor of cavity region) for three brake configurations (x excitation, t=0.1 s,λ=0.8).
Due to the change of the position of relative high pressure induced by dropped circumferential velocity, as shown in the right of Fig.11,the tangential force acting on the cavity region of the rotor switches from positive value to negative value when the brakes are installed at the seal entrance, indicating that the tangential force will restrain the rotor forward whirl and thus enhance the rotor stability. In addition, the radial force acting on the cavity region of the rotor changes from positive value to negative value when the brakes are arranged at the seal entrance, implying that the radial move is limited and thus improve the centering ability. On the other hand, a larger pressure fluctuation in the cavity region is discovered when the distance between the brake trailing edge and the first tooth changes from 1.5 mm to 0 mm,and this can be explained by the circumferential momentum equation later and will lead to an increase in the magnitude of the response force.Another interesting observation is that phase angle of the response force varies less than 0.9% although the two axial brake configurations occupies remarkably different circumferential velocity in the cavity region,and this is ascribed to the circumferential limit of the upstream brakes. Therefore, as a final result of the pressure fluctuation and the phase angle of the response, the tangential component force and radial component force for the brake configuration withd=0 mm are both strengthened in the magnitude (increase by about 60%) compared to the brake configuration withd=1.5 mm, and this indicates that the rotor stability and the centering stability in the cavity region are further increased when the brakes are arranged against the first tooth.
In general,the descending order in the total tangential force acting on the rotor is the no-brake configuration, the brake configuration withd=1.5 mm and the brake configuration withd=0 mm,hence yielding an inverse increase in the overall effective damping, which is consistent with the results in Fig. 9(b).
On the other hand, the transient flow field atxexcitation andt=0.1 s can be simplified as a steady flow field with an eccentric rotor when neglecting the tangential whirling velocity of the rotor, and then the circumferential momentum equation23for the steady-state problem is given as follows.

Where ρiis the density of theith cavity,Viis the circumferential velocity of theith cavity, θ is the angle,Aiis the crosssection area of theith cavity,miis the leakage flow rate of theith cavity,Piis the pressure of theith cavity, τri, τsiare the rotor and stator shear stress of theith cavity, αri, αsiare the length of rotor and stator of theith cavity.
In Eq (10),mican be treated as a constant variable due to the little difference less than 0.8% between two axial brake configurations and ρiis actually hardly influenced by two brake configurations;Ai,D0, αri, αsiare the constant variables,therefore,the item(Ⅰ)is decreased with dropped circumferential velocity.As illustrated in Fig.7,the slope in the cavity region is nearly identical for two axial brake configurations;hence, the item (Ⅱ) keeps constant. On the other hand, the dropped circumferential velocity will cause an increase in the circumferential velocity gradient near the rotor surface and a decrease in the circumferential velocity gradient around the stator surface, therefore, τriis increased with the dropped circumferential velocity while the τsiis decreased with the dropped circumferential velocity, that is, the item (Ⅳ) is increased with the dropped circumferential velocity. To guarantee the balance between the left and the right of Eq. (10),the item(III)must be decreased with the dropped circumferential velocity, that is, the pressure fluctuation in the circumferential direction is strengthened with the reduced circumferential velocity, and this is why the brake configuration withd=0 mm occupying lower circumferential velocity produces larger pressure fluctuation in the cavity region when compared to the brake configuration withd=1.5 mm.
5. Conclusions
An investigation of the effect of axial distance between the trailing edge and the first tooth on the leakage performance and rotordynamic coefficients was conducted at two typical inlet preswirl ratios for labyrinth seals, and the predicted results for two axial brake configurations were in comparison with the results for no-brake configuration. The conclusions obtained are listed as follows.
Introducing swirl brakes at the seal entrance will not damage the seal performance, and the difference in the leakage for two axial brake configurations is minor and can be neglected.The circumferential velocity at the seal entrance can be effectively impeded by the brakes, and the brake configuration against the first tooth produces lower circumferential velocity in the downstream of the brakes as a result of the larger counter-clockwise vortex moving from the brake trailing edge to the brake leading edge when compared to the brake configuration away from the first tooth.
When the brakes are introduced at the seal entrance, the remarkably dropped cross-coupling stiffness causes an increase in the effective damping compared to the no-brake configuration. Besides, the further increased effective damping and dropped crossover frequency reveal a better rotor stability when the distance between brakes and the first tooth decreases to zero. Therefore, from a point view of improving rotor stability, it’s better to install swirl brakes against the first tooth,and this requires the swirl brakes and the labyrinth seal are designed and manufactured simultaneously so that the axial conditiond=0 mm can be easily guaranteed.
When seal cavities are divided into two regions at the leading edge of the first tooth: the brake region and the cavity region,the tangential force acting on the brake region is hardly influenced by brake configurations, however, the tangential force acting on the cavity region is obviously improved in terms of restraining rotor forward whirl when swirl brakes are installed at the seal entrance.Besides,the dropped circumferential velocity in the downstream of brakes will cause larger pressure fluctuation in the circumferential direction and thus generates larger tangential force to restrain the rotor forward whirl when the distance between brakes and the first tooth decreases to zero.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors thank the anonymous reviewers for their critical and constructive review of the manuscript.This study has been funded by the National Key R&D Program of China (No.2017YFB0601804)and the National Natural Science Foundation of China (No. 51776152).
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Tangling and instability effect analysis of initial in-plane/out-of-plane angles on electrodynamic tether deployment under gravity gradient
- Aerodynamic periodicity of transient aerodynamic forces of flexible plunging airfoils
- Experimental and computational investigation of hybrid formation flight for aerodynamic gain at transonic speed
- Tomography-like flow visualization of a hypersonic inward-turning inlet
- Hypersonic reentry trajectory planning by using hybrid fractional-order particle swarm optimization and gravitational search algorithm
- A theoretical and 1-D numerical investigation on a valve/valveless air-breathing pulse detonation engine
