Real-time mosaicking for infrared videos from an oblique sweeping camera
2021-03-16JizhenLUFngdeSUNJingDONGSongliHANAngSU
Jizhen LU, Fngde SUN, Jing DONG, Songli HAN, Ang SU
a School of Aeronautics and Astronautics, Central South University, Changsha 410083, China
b Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China
KEYWORDS Fast Fourier transform;Least squares matching;Map fusion;Mosaic;Real-time;Template matching
Abstract Image mosaicking is widely used in Geographic Information Systems (GISs) for largescale ground surface analysis.However,most existing mosaicking methods can only be used in offline processing due to the enormous amounts of computation.In this paper,we propose a novel and practical algorithm for real-time infrared video mosaicking. To achieve this, a novel fast template matching algorithm based on Sum of Cosine Differences (SCD) is proposed to coarsely match the sequential images.The high speed of the proposed template matching algorithm is obtained by computing correlation with Fast Fourier Transform(FFT).We also propose a novel fast Least Squares Matching(LSM)algorithm for inter-frame fine registration,which can significantly reduce the computation without degrading the matching accuracy. In addition, the proposed fast LSM can effectively adapt for noise degradation and geometric distortion. Based on the proposed fast template matching algorithm and fine registration algorithm, we develop a practical real-time mosaicking approach which can produce seamless mosaic image highly efficiently. Experiments on synthetic and real-world datasets demonstrate that the proposed algorithm is not just computationally efficient but also robust against various noise distortions.
1. Introduction
Image mosaicking is the construction of a large image by composing smaller image patches.The mosaic image integrates the rich information content of images and increases the field of view. Therefore, image mosaicking is widely used in Geographic Information System (GIS) applications for largescale ground surface analysis.
In this work,the infrared camera is mounted on an oblique sweeping device which is carried by an Unmanned Aerial Vehicle (UAV). The sweeping rate is 25 Frames Per Second (FPS)and the resolution of the infrared camera is 640×512. The swept area will increase as the UAV flies forward, which is shown in Fig. 1. Long focal length and small field of view are employed for capturing image with high ground resolution.The inter-frame overlap area is very small. In the flight direction,the average inter-frame overlap rate is about 15%.In the scan direction, the average inter-frame overlap rate is about 25%.In addition,the valid overlap area rate will float between 10% and 40% because of the pose error. Therefore, the ratio between overlap area and search area could be very small.This will pose a challenge to the inter-frame matching which is a crucial step in video mosaicking. In view of the above facts,mosaicking is required for integrating the video sequence into a large image with a bigger view.
These existing orthomosaic generation methods1-4can produce high-accuracy mosaic image from aerial photographs.However,these methods cannot be used for real-time mosaicking due to the expensive computation cost. Besides, the image registration algorithms5,6employed by these orthomosaic generation methods are developed for high-quality visible light image. However, the infrared video stream sent back from a UAV may carry with motion blur, radio noise, and the intensity change caused by the gain variations of the infrared camera, which are hardly to be correctly matched with these existing image registration algorithms.
Motivated by the limits of the existing methods and practical demands, we propose a novel and practical method for mosaicking the infrared videos in real time.
The overview of the proposed algorithm is shown in Fig.2.Firstly,the input frames are corrected to orthoimage according to the Positioning and Orientation Systems(POS)information associated with each image. The corrected frame is then input into a coarse matching algorithm based on Sum of Cosine Differences (SCD) for estimating the translation offset between frames.After the coarse matching,a fine registration algorithm is employed for estimating the inter-frame homography. During the map fusion, a global optimization thread and a realtime mapping thread work cooperatively for generating seamless mosaic image. There are two main contributions in our work.

Fig. 1 Image capturing process of sweeping camera.
1.1. A novel fast template matching algorithm based on SCD
After the captured images are corrected to orthoimages, we can coarsely match the inter-frame by using the template matching with translation search only. Even so, the computation cost of normal template matching algorithm is too expensive for real-time mosaicking.
To handle this problem, we propose a novel fast template matching algorithm based on SCD to perform coarse matching. The proposed template matching algorithm has two merits. Firstly, the correlation process can be effectively accelerated with Fast Fourier Transform (FFT). Secondly,the proposed template matching algorithm is robust against the gray change caused by gain variation.

Fig. 2 Flowchart of proposed mosaic algorithm.
1.2. A novel fine registration algorithm for seamless map fusion
After the image correction,small projective distortion may still exist on the corrected image due to the errors of the camera pose. However, the template matching with translation search cannot address the projective distortion. Therefore, a fine registration algorithm with homography estimation is required for seamless map fusion.
Least Squares Matching(LSM) with affine estimation7is a very useful algorithm for matching two image patches with high accuracy. However, LSM is very computationally expensive,which cannot be used for real-time mosaicking.8Furthermore, the affine model is not accurate enough for the estimation of global transformation between images because it is not strict in terms of the projective imaging model.9Bethmann and Thomas proposed an advanced least-squares matching algorithm which uses the projective transformation model to handle the geometric distortions between images.9However,their method is even more expensive in computation because the polynomial functions of their method are much more complicated compared with the LSM using affine transformation model.
In this work, we propose a novel fast LSM based on steerable filters. Compared with traditional LSM algorithm,7the proposed algorithm can significantly reduce the computation without degrading the matching accuracy. In addition, the proposed LSM can effectively adapt for noise degradation and geometric distortion.
In the remaining parts of this paper,Section 2 describes the related works.The proposed fast template matching algorithm based on SCD is presented in Section 3. The fine registration algorithm for inter-frame homography estimation is described in Section 4. The global optimization and the real-time map fusion are introduced in Section 5. In Section 6, we compare the proposed image matching algorithm with other state-ofthe-art algorithms and conduct a thorough evaluation on the proposed mosaicking method with synthetic and real-world datasets. Finally, the conclusion of this work is presented in Section 7.
2. Related work
Orthomosaic generation based on Structure from Motion(SfM)is a mature choice for producing mosaic image with aerial photographs. There are lots of implementation of this type of method such as commercial software Context Capture,1Pix4DMapper,2and the open-source project OpenDroneMap.3For these types of solution, all images ready for mosaicking have to be prepared before the computation because the global optimization based on bundle adjustment is employed.In addition,they often take hours to finally generate the orthomosaic image.4Therefore,orthomosaic generation based on SfM cannot be used for real-time application.Botterill et al.10proposed a real-time aerial image mosaicking algorithm to provide an operator with a larger field-of-view. To achieve high performance,the Bag-of-Words image representation11,12and a Sample Consensus based robust estimation framework13are employed by this method to efficiently match images.However,this method only integrates the mosaic image with several local frames,which is not suitable for incremental mosaicking usage.Bu et al.4proposed a real-time incremental image mosaicking method based on monocular Simultaneous Localization and Mapping (SLAM).12,14,15Compared with SfM, SLAM has the advantage of real-time performance.However,SLAM also requires substantial overlap area between adjacent frames;otherwise SLAM will fail to track the inter-frame motion.16
Real-time image mosaicking requires a fast and robust image matching algorithm to estimate the inter-frame transformation. There are many different image matching algorithms in photogrammetry and computer vision, which can be roughly divided into two groups: feature matching and template matching.The feature based matching algorithms assume that shared features can be reliably detected and matched between images so that there are sufficient corresponding features to estimate the two-dimensional global transformation.17The state-of-the-art feature matching algorithms such as Scale-Invariant Feature Transform (SIFT)5,18and Speeded-Up Robust Features (SURF)6usually cannot achieve real-time performance on personal computer without GPU support.To solve this problem, more efficient feature detectors19and feature descriptors20are proposed,21which are frequently employed by the recent works on real-time SLAM14,16and real-time mosaicking.4,10Compared with template matching,feature based matching is more adaptive to geometric distortion. However, it is very difficult to match the share features when overlap area is too small.17Recent studies suggest that noise degradation, feature-less texture, and motion blur will make repeatable feature detection difficult;in those cases,template methods are preferred.17,22
Full Search (FS) template matching algorithms usually require extensive calculations, which make them impractical for some real-time applications. To reduce the computational burden,many fast algorithms have been proposed.A frequent approach is image pyramid,which can reduce the search space and time cost on each window simultaneously. However,image pyramid can produce an incorrect result because the optimal result may be missed during a coarse level search.23
An alternative solution is to accelerate the template matching process with Full Search (FS)-equivalent algorithms.24,25The main advantage of FS-equivalent algorithms is that they can accelerate template matching process while yielding the identical result as an FS algorithm. Nevertheless, the FSequivalent algorithms may take more time than the FS algorithm if the image is seriously corrupted by noises.23
Fast Fourier Transform(FFT)is employed by the fast Normalized Cross Correlation (NCC) template matching algorithm26and the fastL2norm template matching algorithm25to accelerate the searching process. They are also FS algorithms, but the computation of the searching process based on FFT is invariant to noise degradation. Therefore, FS algorithms based on FFT usually achieve better performance than FS-equivalent algorithms for matching image with noise degradation.
3. Fast template matching based on SCD
In this chapter, we first introduce the similarity measurement used by the proposed template matching algorithm. Then,we will describe the mask operation and how to accelerate the search process with FFT.
3.1. Similarity measurement based on SCD
Referring to the image t and image t′as vectors in Rl×h, SCD between the two images can be calculated by

where αiis the gradient orientation of image t,and βiis the gradient orientation of image t.The adaptive ability to the intensity change will be improved by matching the images based on the gradient orientation instead of image gray.22
SCD is a similarity measurement. SCD will achieve the maximum value 1 if image t and t′are identical. On the contrary,SCD will achieve the minimum value-1 when the absolute difference between αiand βiis always equal to π.
3.2. Fast correlation with FFT
The search process with mask operation is accelerated with FFT. As depicted in Fig. 3, the input image will be no longer a full frame after it is corrected to orthoimage.There are invalid areas in the frame. A mask operation is employed by the search process of the proposed algorithm to handle the invalid areas. The searching process of the template matching based on SCD mainly consists of two steps.
Step 1.the similarity between the template and all the windows in the base image are estimated with SCD measurement.
Step 2.the position of the window with the max similarity to the template will be output as the matching result. Apparently,Step 1 accounts for the main computation amount of the searching process. Fortunately, Step 1 can be efficiently accelerated with FFT.
The SCD measurement in Eq. (1)with mask operation can be calculated as


Fig. 3 Inter-frame matching.
Therefore,the SCD′measurement will be accumulated only when both the pixel in the template and the pixel in the window are in the valid area.
During the searching process,we need to calculate SCD′for each candidate window,which means that we need to perform three convolutions according to Eq.(2),two for the numerator and one for the denominator. Convolution in the spatial domain is very computationally expensive, because the template must be correlated with each candidate window in the base image.For accelerating this process,we perform the convolutions in frequency domain.
According to the convolution theorem, the convolution in the spatial domain is analogous to the multiplication in the frequency domain,27which can be formulized as

wheret(x,y)*b(x,y) stands for the convolution of the two images in the spatial domain, andT(u,v)B(u,v) stands for the pixel-to-pixel multiplication of the two transformed images in the frequency domain. The two processes are related by the forward and inverse Fourier transforms which can be realized in FFT.
Therefore, the searching process of SCD′can be estimated with 3 convolutions, which can be accelerated with FFT as follows:

where bxand byare thexandycomponents of the base image,mbis the mask of base image,txand tyare thexandycomponents of template image, mtis the mask of template image,FFT stands for forward FFT, and IFFT stands for inverse FFT.
4. Fine registration based on fast LSM
The coarse matching based on SCD aims for fast estimating global translation offset between the corrected images. Due to the pose error, small projective variations may still exist on the corrected images. For seamless map fusion, a fine registration algorithm with homography estimation is required to estimate the global transformation between the corrected images. In this section, we will first introduce the ordinary LSM algorithm, then describe the proposed fast LSM algorithm in detail, and finally elaborate how to estimate the inter-frame homography.
4.1. Ordinary LSM
The basic idea of LSM can be formulized by
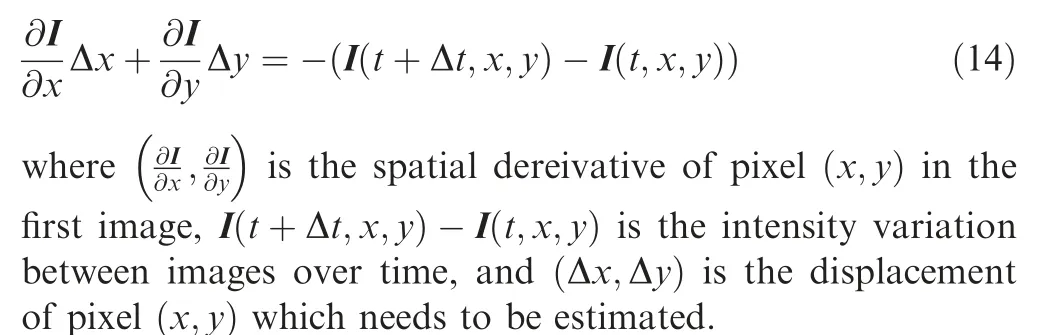
In addition, affine model can be introduced to describe the geometry transformation as follows:

where Δr0,Δr1,Δr2,Δr3,Δr4,Δr5are the undetermined parameters of affine model. Substituting Eqs. (15) and (16) into Eq.(14) and making it simplified, we can derive the final LSM equation as follows:

where · stands for dot product operation and the vectors∂Iandrare given in Eqs. (14) and (15) respectively.
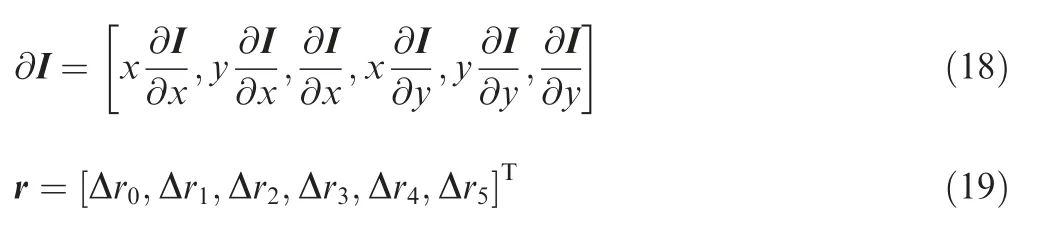
For each pixel of the image, a function will be created according to Eq. (17). Therefore, the function group of ordinary LSM will be enormous. Since the number of equations exceeds the number of undetermined parameters, the function group can be solved by least squares estimation. Actually, the final results are usually acquired by the iterative LSM.
4.2. Fast LSM
To reduce the computation cost, one can build the function group with only part of the pixels.However,the matching reliability will be degraded if fewer pixels are employed for the estimation.
To solve the problem, we propose a novel fast LSM. Each equation of its function group is built on the whole image instead of one pixel. Specifically, we first project the two sequential images and the derivatives of the first image to a steerable filter Gi, and then substitute the coefficient of Eq.(17) with the project results. We can derive the new equation as follows:

where I(t)and I(t+Δt)are the two sequential images,and ∂I′consists of 6 derivative images of the first image,which is given in
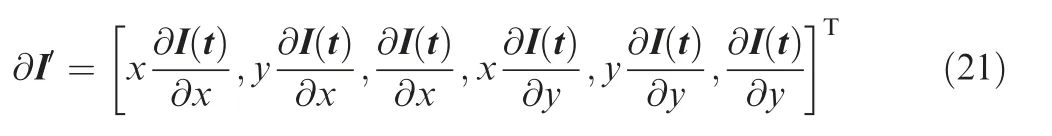
For each steerable filter,we establish a function for the two sequential images according to Eq. (20). Therefore, the function group of the proposed LSM is much smaller than that of the ordinary LSM, because the steerable filters employed by the proposed LSM are much less than the pixels of the image.
There are 7 steerable filters employed by the proposed algorithm,which are given in Fig.4.G2is the second derivative of a Gaussian filter, which can be formulized by

In Eqs. (22) and (23), σ represents the scale of the filter,which is set to 7, 9, and 11 pixels. Therefore, there are totally 21 equations in the function group of the proposed LSM algorithm.
According to the steerable theory proposed by Freeman and Adelson,28the 7 steerable filters given in Fig. 4 are sufficient to shiftG2arbitrarily in both phase and orientation. In addition, there are two important properties about the 7 steerable filters. First, the 7 steerable filters are zero Direct Current (DC) response, which means that the responses of the filters will be unchanged when the global brightness adds a constant.29This property will improve the adaptability of the matching algorithm for illumination variation. Second,the radial components of the basis filters are quite close to the Gauss component. When two images are not entirely aligned, the misalignment in the marginal area of the image is usually severer than that in the center area. The second property will make the affine model estimation put more weight on the pixels around the center of the image, which can enhance the adaptability to misalignment and geometric distortion.
4.3. Inter-frame homography estimation
The proposed homography estimation is based on the tie point correspondences between two adjacent frames, which mainly consists of three steps.
Step 1.Key points are selected on the overlap area by adopting the feature point selecting approach introduced in Ref. 30. This approach can scale the number of the selected key points for limiting the computation cost spend on tracking these key points.In addition,this approach makes the selected points evenly spread on the overlap area for adapting the local occlusion and the local geometric distortion.

Fig. 4 7 steerable filters employed by proposed fast LSM algorithm.
Step 2.Tie point correspondences are calculated by

where T is the vector of the global translation offset of interframe, which is estimated by the SCD template matching,and A is the matrix of local affine transformation around a selected key point P, which is estimated by the fast LSM algorithm.
Step 3.We use Random Sample Consensus (RANSAC)algorithm31to estimate the inter-frame homography with those tie point correspondences calculated in the last step.
5. Map fusion
After the inter-frame homography estimation, the mosaic image can be generated by incrementally mapping each input image to a predetermined plane. However, this incremental mosaicking process will cause accumulated errors as the mosaic image grows, which will lead to significant misalignment on the mosaic image soon or later. Global optimization can remove the accumulated errors. However, all the images have to be prepared before the optimization. Therefore, the mosaic image cannot be generated in a real-time or continuous way, if global optimization is employed.

Fig. 5 Flowchart of map fusion.

Fig. 6 An image from dataset and its distorted images.
To solve this problem, we propose a novel map fusion approach which not just generates the mosaic image in real time but also can remove the accumulated errors. This map fusion approach consists of a global optimization thread and a real-time mapping thread.
5.1. Inter-frame homography estimation
5.1.1. Input
In our work, the global optimization works as an online process.Therefore,we cannot put all the images into the optimization process due to the limit computing resource. The inputs include the recently arrived images within a time window,the image coordinates of tie point measurements, and the correction homographs for mapping the input images to orthoimages. The correction homographic matrix Hcis calculated according to the POS information associated with each image.The tie point correspondences between the adjacent frame in both the sweeping direction and the flight direction need to be calculated for the global optimization.

Fig. 7 Comparison of matching accuracy between FLSM and TLSM.
5.1.2. Optimization
The global optimization algorithm will refine the initial homographs for globally minimizing the sum of coordinate measurement residuals of the squared tie point image. The details of the adjustment are described in Ref. 32.
5.1.3. Output
The outputs of the optimization are the refined homographic matrix Heof each image and a mosaic image. Each image can be mapped to the mosaic image according to the following equation:

where I is the image point on the input image,and I′is the corresponding image point on the mosaic image.
5.2. Real-time mapping thread
This thread incrementally maps the input image to the mosaic image.It is supposed that a mosaic image is generated by global optimization thread withnimages from the(j-n)-th image to thei-th image. Thej-th image, which is arrived after thei-th image, can be mapped to the mosaic image by


Fig. 8 Two examples for comparing FLSM and TLSM.

Table 1 Time statistics of FLSM and TLSM.
where Hiis the homography which maps thei-th image to the mosaic image.It can be calculated according to Eq.(25).Hi,jis the homography which maps a point from thei-th image to thej-th image. Eq. (26) is also applicable at the very beginning,when there is no mosaic image returned by the global optimization thread. To do that, one can change Hito H1, which is the homography that maps the first image to a predetermined image.
The real-time mapping thread and the global optimization thread are concurrent threads as depicted in Fig. 5. When the optimization thread is processing, the real-time thread maps the new arrived image to the last mosaic image. When a new mosaic image is generated by the optimization thread,all the images which are not mapped to the new mosaic image have to remap to the new mosaic image. The global optimization and the remapping process are executed in the background. Therefore, the foreground mosaicking process is real-time and continuous.

Table 2 Two types of degeneration.
6. Results and discussion
We developed a series of experiments to investigate the performance of the proposed image mosaicking algorithm. First, we compare the proposed Fast LSM (FLSM) algorithm with Traditional LSM(TLSM) algorithm.7Second,the advantages of the proposed inter-frame matching algorithm over the stateof-the-art matching algorithms, such as SIFT,5SURF,6Oriented FAST and Rotated BRIEF (ORB)21DeepMatching(DM),33and Dense Adaptive Self-Correlation (DASC),34are verified. Finally, we evaluate the whole approach with experiments on synthetic and real-world datasets.

Table 3 Matching accuracy of the investigated algorithms.

Table 4 Time statistics of the investigated algorithms.
6.1. FLSM vs. TLSM
First, the matching accuracy of the two algorithms is evaluated. A dataset consisting of infrared image pairs is adopted for this evaluation. Three types of degeneration are added to these image pairs, which include light change, projective distortion,and image noise.Fig.6 illustrates an image and its distorted images with these degenerations.This dataset is used for evaluating the matching accuracy of FLSM and TLSM. The results are shown in Fig.7.The matching accuracy is measured by the average Root Mean Squared Error (RMSE) in pixel.The matching accuracy of FLSM and TLSM are comparable for the original dataset.The light change almost has no impact on the matching accuracy of both algorithms. However, the matching accuracy of TLSM is seriously degraded by the noise and projective distortions. On the contrary, these two distortions have much less impact on the matching accuracy of FLSM. The testing results indicate that FLSM has better adaptability for the noise and projective distortion, compared with TLSM. Two compared examples are given in Fig. 8.From the enlarged view, we can see that FLSM successfully matched the two images,while TLSM mismatched two images,in both cases.
The computation efficiency of the two algorithms is also compared. We conducted this experiment on a laptop with an Intel Core i7 2.8 GHz CPU.The results are given in Table 1.We can see that the proposed FLSM algorithm has a distinct speed advantage over the TLSM algorithm.
6.2. Inter-frame matching evaluation
We compared the proposed inter-frame matching algorithm with five state-of-the-art matching algorithms: SIFT, SURF,ORB, DM and DASC. The dataset for this evaluation consists of five infrared video clips captured by a UAV. Further, blur and noise distortions are added to each video clip. Each type of distortion has four noise levels with different Peak Signal to Noise Ratio (PSNR). The details of the two types of distortion are given in Table 2. The matching accuracy is measured by the average Root Mean Squared Error (RMSE) in pixel. The results are given in Table 3.The results indicate that the proposed algorithm (FLSM)has a distinct advantage over SIFT, SURF and ORB for adapting the blur and noise distortions. We believe the main reason is that the proposed algorithm is based on template matching algorithm which is more robust for noise and blur distortions compared with feature point based matching algorithms.17DM and DASC also showed good performance for adapting the blur and noise distortions. However,they require enormous computation for achieving that, as shown in Table 4. This makes them cannot be applied to real-time applications.
The computation efficiency of the investigated algorithms is also compared. The results are given in Table 4. We can see that the proposed algorithm(FLSM)is the most computationally efficient one in the investigated algorithms.
6.3. Mosaicking test
We evaluated the proposed algorithm with video clips including real infrared video clips captured by a UAV and synthetic video clips.Some of these synthetic video clips are synthesized by adding artificial degenerations to these real infrared video clips. The results show that the proposed algorithm is able to handle the serious light change,motion blur,and noise distortions.An example of mosaic image produced by the proposed algorithm is given in Fig. 9.
The test result of a synthetic video is provided in Fig. 10.We can see that the RMSE will grow as the length of video clip increases. This is because the inter-frame matching errors will accumulate if the global optimization is not adopted. When global optimization is applied, the proposed mosaicking algorithm can maintain the RMSE below 1 pixel.

Fig. 9 An example of mosaic image produced by proposed algorithm.

Fig. 10 RMSE versus video length of proposed algorithm.
7. Conclusions
Real-time infrared video mosaicking is a very challenging task for the existing methods due to the limited time and the requirement of high reliability. In this paper, we propose a novel and practical mosaicking algorithm for this task. There are two main contributions in our work. First, we propose a novel fast template matching algorithm based on SCD for inter-frame coarse matching. The measurement of this algorithm is invariant to light change, and the searching process of this algorithm can be efficiently accelerated with FFT. Second,we propose a novel fast LSM based on steerable filters for inter-frame fine registration. Compared with traditional LSM algorithm, the proposed algorithm can significantly reduce the computation. In addition, the proposed fast LSM can effectively adapt for noise and geometric distortion.
The experiments on synthetic and real-world datasets verified that the proposed mosaicking algorithm can produce seamless mosaic image for infrared videos in real time.
The gain variation of infrared camera will produce interframe light change. Although the proposed matching algorithm can adapt to this problem, the gray inconsistency caused by the light change is not removed from the mosaic image.
Acknowledgements
This paper is supported by the National Natural Science Foundation of China (No.61802423)and the Natural Science Foundation of Hunan Province, China (No. 2019JJ50739).
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Tangling and instability effect analysis of initial in-plane/out-of-plane angles on electrodynamic tether deployment under gravity gradient
- Aerodynamic periodicity of transient aerodynamic forces of flexible plunging airfoils
- Effects of swirl brake axial arrangement on the leakage performance and rotor stability of labyrinth seals
- Experimental and computational investigation of hybrid formation flight for aerodynamic gain at transonic speed
- Tomography-like flow visualization of a hypersonic inward-turning inlet
- Hypersonic reentry trajectory planning by using hybrid fractional-order particle swarm optimization and gravitational search algorithm
