High-fidelity trajectory optimization for aeroassisted vehicles using variable order pseudospectral method
2021-03-16RunqiCHAIAntoniosTSOURDOSAlSAVVARISSenchunCHAIYunqingXIA
Runqi CHAI, Antonios TSOURDOS, Al SAVVARIS, Senchun CHAI,Yunqing XIA
a School of Aerospace, Transport and Manufacturing, Cranfield University, Bedfordshire MK43 0AL, United Kingdom
b School of Automation, Beijing Institute of Technology, Beijing 100081, China
KEYWORDS Aeroassisted vehicle;High-order;Radau pseudospectral method;Six-degree-of-freedom;Trajectory design;Variable order
Abstract In this study, the problem of time-optimal reconnaissance trajectory design for the aeroassisted vehicle is considered. Different from most works reported previously, we explore the feasibility of applying a high-order aeroassisted vehicle dynamic model to plan the optimal flight trajectory such that the gap between the simulated model and the real system can be narrowed.A highly-constrained optimal control model containing six-degree-of-freedom vehicle dynamics is established.To solve the formulated high-order trajectory planning model,a pipelined optimization strategy is illustrated.This approach is based on the variable order Radau pseudospectral method,indicating that the mesh grid used for discretizing the continuous system experiences several adaption iterations. Utilization of such a strategy can potentially smooth the flight trajectory and improve the algorithm convergence ability. Numerical simulations are reported to demonstrate some key features of the optimized flight trajectory.A number of comparative studies are also provided to verify the effectiveness of the applied method as well as the high-order trajectory planning model.
1. Introduction
In recent years, aeroassisted vehicles have attracted considerable attention in aerospace industry due to their potential and reliability for long-endurance, low-energy and propellent-free applications1,2. One important feature of this type of vehicle is that they have the flexibility to only use aerodynamic forces to execute maneuvers3, thereby completing various atmospheric flight missions4,5. Among these applications,the problem of inaccessible area reconnaissance has been recently recognised as an important research subject6,7. Since different mission-related requirements need to be considered8,the observation flight trajectory planning tends to play a key role in the success of the mission9,10. This is because a wellplanned maneuver trajectory is of particular importance to guarantee safety issues and provide enhanced control performance.
During the last couple of decades, significant amount of efforts have been devoted by researchers and aerospace engineers on developing promising trajectory planning methods.By reviewing the literature,we are able to find numerous effective trajectory planners reported especially for space vehicle atmospheric flights.For example,the authors in Ref.11studied and addressed the hypersonic vehicle atmospheric entry problem. In this paper, a global collocation method was adopted and the problem was formulated with an emphasis on multiple no-fly zone constraints. Similarly, a constrained Particle Swarm Optimization-based (PSO) trajectory planner was proposed in Ref.12to search the end-to-end trajectory for hypersonic reentry vehicles. To rapidly construct the landing footprint, an interpolation model was also utilized for the bank angle profile.
To obtain enhanced convergence performance of the optimization process, an improved PSO-based trajectory planning algorithm was constructed in Ref.13. Subsequently, this approach was used to optimize the glide trajectory of the hypersonic reentry vehicle. Taking into account multiple process constraints and terminal constraints,a Gauss pseudo spectral method-oriented trajectory generator was designed in Ref.14for a solar-powered aircraft.In addition,by combining genetic algorithm,PSO and simulate annealing,a hyper heuristic trajectory generator was suggested in Ref.15to optimize the flight trajectory of the satellite launch vehicle.
It should be noted that most of these reported works apply the so-called direct transcription strategy where a finite set of mesh grids connecting the initial and terminal pose is firstly applied to discretize the searching space.Then numerical optimization techniques are used to explore the optimal vehicle state/control solutions at these temporal nodes. Based on the reported simulation results, it is undeniable that all the aforementioned planners have the capability of exploring feasible and near-optimal flight trajectories for aircrafts or spacecrafts.However, most of them only formulated the trajectory optimization problems using the Three-Degree-Of-Freedom (3-DOF) dynamic model, which means the model fidelity tends to be decreased.
Model fidelity can be referred to the degree to which a model reproduces the characteristics of a practical system16.In atmospheric trajectory optimization problems, researchers/engineers often apply a lower-fidelity dynamics to describe the movement of a flight vehicle17,18. For example, it is common to consider the vehicle as a point-mass. The resulting solutions are therefore used for preliminary analysis or for approximating solutions to higher-order dynamics. Although using a lower-fidelity dynamic model can be suitable for planning feasible trajectories with respect to the vehicle position and velocity variables, these trajectories can be unrealizable for a physical system (e.g., with respect to forces and moments). In addition, compared to high-fidelity models,atmospheric trajectory planning algorithms based on lowfidelity models might pose a potential safety concern. Hence,in this paper we are interested in exploring the feasibility of applying a high-fidelity vehicle dynamic model to plan the optimal trajectory.
In Ref.6and Ref.19we have investigated the 3-DOF aeroassisted vehicle reconnaissance mission by applying a typical global collocation method(e.g.,the Radau pseudospectral method developed in Ref.20). The applied method builds the optimal flight trajectory between the pre-assigned initial point and the target position on a fixed set of mesh grid. This work provides improvement in terms of model fidelity, solution accuracy as well as result analysis. More precisely, the specific research object, along with the main contributions of this paper, can be summarised below:
(1) We extend the original problem formulation to a Six-Degree-Of-Freedom (6-DOF) aeroassisted vehicle reconnaissance trajectory planning model with flight time minimization.
(2) Due to the complexity of vehicle dynamics and constraints, we apply a pipelined optimization strategy based on a variable order Radau pseudospectral method to tackle the problem.
(3) Detailed comparative results are provided to analyze the difference of the two models and to illustrate the validity of applying the variable order pseudospectral method for the considered problem.
The remaining parts of this article are outlined as follows.In Section 2,we build the time-optimal reconnaissance maneuver optimization problem. The translational and rotational dynamics of the aeroassisted vehicle are introduced. Various constraints and the main objective function are also formulated in this section. In Section 3, the Radau pseudospectral method, together with the mesh grid adaptive strategy is recalled. A detailed simulation study including the obtained optimal trajectory and comparative results will be presented in Section 4.Finally,concluding remarks are given in Section 5.
2. Time-optimal reconnaissance maneuver optimization problem
In this section,two sets of differential equations are firstly presented to formulate the 3-DOF and 6-DOF model of the aeroassisted vehicle. Following that, mission constraints required to be considered during the time-optimal reconnaissance maneuver are introduced. Finally, an overall trajectory optimization formulation is established.
2.1. Model dynamics
The following three assumptions are used for formulating the dynamic model of the aeroassisted vehicle:
Assumption 1.The aeroassisted vehicle is considered as a rigid-body, thereby eliminating the distortional effects (e.g.,the elastic DOF introduced by the flexible-body).
Assumption 2.During the reconnaissance maneuver phase,since we are interested in finding a strictly gliding descent trajectory, it is assumed that the engine is switched off and no thrust is provided.
Assumption 3.We consider the earth as a symmetrical sphere and ignore the effect caused by Earth’s rotation.
Then, the following set of differential equations can be applied to describe the 3-DOF motion of the aeroassisted vehicle6:

Eq. (1) is also referred to the translational Equations of Motion (EMOs). Variables appeared in this equation arer,φ,θ,V,γ,ψ,α,σ,S,CD,g,CL,ρ, representing the radius, latitude, longitude, speed, Flight Path Angle (FPA), azimuth angle, Angle Of Attack (AOA), bank angle, reference area,drag coefficient, gravity, lift coefficient, and atmosphere density, respectively.
If the flight trajectory is built on the 3-DOF model given by Eq. (1), the effects caused by considering forces and moments have not been fully analyzed. As a result, the accuracy of the result might be reduced. To construct a high-order 6-DOF model of the aeroassisted vehicle, the rotational EMOs for the aeroassisted vehicle should be adhered, which can be written as the following set of differential equations:

Rotational variables appeared in these EMOs are β,p,q,and ν, respectively. To better describe these aeroassisted vehicle-related parameters, their notations as well as physical meanings are summarised and tabulated in Table 1.
2.2. Flight constraints and objective
In the reconnaissance mission, the aeroassisted vehicle should only travel within a safe corridor which is determined by the following three path constraints:



Table 1 Definition of aeroassisted vehicle-related parameters.
In the reconnaissance mission, the primary objective is to overfly a target point specified by the final boundary conditions (e.g., in Eq. (7)) with the total flight time being minimized. Therefore, the mission objective function is given by:

2.3. Overall trajectory optimization formulation
Summarizing all the mission-related information stated in previous subsections, an overall trajectory optimization formulation can be established which has the general form of

in which Φ,f(·,·),g(·),b(·) denote the objective function Eq.(8) in Mayer form, EMOs, path constraints, and boundary constraints given by Eq. (1), Eq. (2), Eqs. (3)-(5)), and Eq.(6), respectively. x=[r,φ,θ,V,γ,ψ,α,σ,β,p,q,ν]∈R12is the system state vector and u=[Mx,My,Mz]∈R3is the control vector. (x*(t),u*(t)) stands for the optimal solution to be searched.
3. Solution method
Exploring the optimal flight trajectory for the aeroassisted vehicle reconnaissance mission constructed in Section 2 can be referred to an optimal control problem. One particular method which has been commonly applied to solve problem Eq.(9)is the pseudospectral direct transcription approach21,22.This approach benefits from its suitability for various aerospace applications and adopts orthogonal collocation technique so as to achieve higher polynomial approximation accuracy21,22. By using different collocation points, various pseudospectral methods have been proposed in the Refs.23,24.In this paper,we explore the capability of applying the Radau Pseudospectral Method (RPM) for the considered high-order trajectory optimization problem.
3.1. Radau pseudospectral method

whereLkstands for the Lagrange polynomials.Using Eq.(10),an approximation with respect to the derivative of the state can be obtained via:

in which Djkrepresents the differentiation matrix related to the LGR nodes. As a consequence, the dynamic constraint is equivalent to:

More specifically, for the considered high-fidelity reconnaissance trajectory design problem, the two sets of EMOs of the aeroassisted vehicle are transformed to algebraic equality constraints. For example, the translational EMOs are further written as

As for the rotational EMOs,the corresponding approximation equations can be achieved analogically.Similar to the system dynamics, the path constraints can also be approximated in the same way, and the original problem is rewritten as a finite-dimensional NonLinear Programming (NLP) problem,which is solvable for mature nonlinear optimization algorithms.
3.2. A pipelined optimization strategy
Due to the complexity of vehicle dynamics and constraints, a direct implementation of RPM on the considered problem might encounter numerical difficulties. This section discusses a pipelined optimization strategy based on a variable order RPM in order to alleviate this problem.
3.2.1. Pre-solve process
The pipelined optimization strategy contains three steps: the pre-solve process,the main optimization process,and the mesh grid update process.For most numerical optimal control softwares,the initial guess value at temporal nodes is obtained via linear interpolation between the user-specified boundary guess value. However, this may result in large constraint violation value, thus restricting the searching space significantly. We attempt to address this issue by adding a pre-solve process,where a PSO-based optimal control method proposed in Ref.25is applied to optimize the following unconstrained optimization model:

where Φ(x(τNk;u))=(x(τNk;u)-xf)2, while g(x,u)≤0 is the compressed form of the path constraints defined in Section 2.In Eq. (14), x(τi;u) denotes the state which is obtained via control discretization and numerical integration of the system equations. Minimizing the objective function defined in Eq. (14) is equivalent to minimizing the constraint violation of the original problem, thus quickly generating a feasible flight trajectory for the aeroassisted vehicle (e.g.,u=(u0,u1,...,uNk-1) and x=(x0,x1,...,xNk)). Then this solution will be used to warmly-trigger the main optimization process which is detailed in the next subsections.
3.2.2. Variable order adaptive process
Since the vehicle dynamics become much more complicated in comparison with the widely-applied 3-DOF model, the mesh grid used to discretize the continuous time system becomes more sensitive with respect to the quality of the flight trajectory. Usually, a large-scale mesh grids is desired to represent the flight trajectory. However, a large-scale fixed mesh grids may result in failures in terms of the algorithm convergence.On the other hand, although a small-scale mesh grid can improve the convergence of the optimization process, key characteristics of the optimal flight trajectory may not be captured. Consequently, the mesh grid adaption becomes a vital role in the success of solution finding.
Different from the mesh adaptive strategy used in Ref.19,26,in this work the mesh adaptive process is fulfilled by further exploiting the Legendre polynomial series as suggested in Ref.23,24. Specifically, assume that we are using aNkorder Legendre polynomial to approximate the function x(τ):

in which Ri(τ) is the basis of the Legendre polynomial. The core idea of this mesh adaptive strategy is to apply the decay rate lito assess the smoothness of the function x(τ).Note that if x(τ)is a smooth bounded function,then it can be accurately represented by

If we apply theNkorder approximation given by (15), the error term e can be written as

In Eq. (17) and Eq. (18), the norm is defined by the inner product. For example,

Then the two error terms (e1ande2) can be represented by

Suppose a tolerance value -σ is provided by the user. We define that x(τ) is smooth if σ> -σ and vice versa. If we detect that a mesh interval is not smooth,then the current mesh interval is divided into subintervals. On the other hand, if the current mesh is smooth, the approximation can be further improved by enlarging the polynomial degrees.More precisely,if σ> -σ,we intend to increase the number of nodes in the current mesh interval and this number is calculated by

whereHdenotes the index of the mesh grid,while ∊is the userspecified accuracy tolerance. If σ< -σ, we intend to divide the current mesh grid. This is achieved via two steps. Firstly, we calculate the total number of nodes of the new mesh grid via

3.2.3. Design parameter selection
It is true that the implementation of the variable order pseudospectral method will introduce some design parameters which may have impacts on the algorithm performance and convergence ability. Therefore, a proper design parameter selection process is needed to start the solution-finding iteration.This process becomes even more important for the trajectory optimization in the real application. However, selecting proper design parameters (e.g., -σ and ∊) might be problemdependent. Here, we present an interactive strategy for the design parameter selection process. By setting an initial -σ,the problem can be solved and the results will be presented to the designer.If the designer is not satisfied with the planning results, the design parameters can be reassigned based on the behaviour of the obtained solution. Specifically, if the current results oscillate significantly or contain some discontinuities,it would be beneficial to reassign a largerand vice versa.On the other hand, ∊ can be initially set to a large value (e.g.,∊=1×10-3). This will improve the convergence rate of the optimization process. Subsequently, the designer can use the low-accuracy solution as the starting point and tighter the tolerance level to obtain more accurate results.
4. Simulation results
4.1. Simulation setting
As indicated in Section 2, some task-related and vehicledependent parameters should be assigned to construct the high-fidelity aeroassisted vehicle reconnaissance trajectory optimization model. For example, the variable initial conditions and targeted final states are provided in Table 2 and Table 3, respectively.
The variable physical limits,rate/path constraints are set as follows:

Note that 1 lb=0.45359 kg, 1 ft=0.3048 m, 1 Btu/ft2/s=1.135654 W/cm2/s, 1 slug/ft2=1.35582 kg/m2, g=9.81 m/s2and 1 lb·ft=1.35582 N·m.

Table 2 Variable initial conditions.

?
The vehicle parameters are set as follows:

The simulations were performed under Windows 7 and Intel(R) i7-4790 CPU, 2.90 GHz, with 8.00 GB RAM, while the MATLAB version is R2019a. To run the simulation, the initial mesh grid contains 40 points and the accuracy tolerance value is assigned to ∊=10-6.
4.2. Optimized results of using different models
In this subsection, the optimized results obtained using the low-fidelity 3-DOF model as well as the high-fidelity 6-DOF model are firstly analyzed.More precisely,the optimized translational state and control profiles of these two models are presented in Fig. 1 and Fig. 2, respectively. The corresponding heating rate, dynamic pressure, and normal load profiles are visualized in Fig. 3. In addition, for the 6-DOF model results,the rotational state profiles and the corresponding control moment curves are shown in Fig. 4 and Fig. 5, respectively.
As can be seen from Fig. 1 to Fig. 5, both cases accurately meet the initial and terminal boundary conditions while achieving the same level of accuracy threshold. However, differences can be detected in the obtained solutions.These differences are particulary obvious in terms of path constraint profiles for the low/high-fidelity formulations. This implies that the low-fidelity trajectory results might not be realizable for a high-fidelity system,which means the importance of considering the forces and moments (e.g., rotational variables) in the trajectory optimization process should be emphasized.
Although using a lower-fidelity model can be suitable for planning feasible trajectories with respect to the vehicle translational variables, it might pose a potential safety concern.Therefore,in order to generate a promising solution,it is advocate to apply the investigated high-fidelity model to plan the aeroassisted vehicle reconnaissance trajectory.
Furthermore, a comparison of the trajectory optimization using the pseudospectral method to a convex optimization method is also carried out. It is worth noting that this combinational strategy has become increasingly popular in recent years28,29. The obtained results are displayed in Fig. 1 to Fig. 3 (denoted as ‘‘Con results”). Analysis has been made from two aspects: the optimization strategy simplicity and the algorithm performance.
As for the optimization strategy simplicity, this can be reflected by comparing the required computational time.Specifically, 5.42 s is required for the adaptive pseudospectral method while only 2.07 s is required for the convex optimization.Benefiting from the polynomial complexity of the convex optimization,a roughly 68.81%reduction in terms of the computational time can be achieved.
Regarding the algorithm performance, the solutions obtained using these two strategies generally follow the same trend. However, slight differences can be detected in the state trajectories. This can be attributed to multiple reasons such as the linearization process used to convexify the problem,and the final mesh grid obtained via the strategy introduced in Section 3.3.2.
We have also tested the performance of applying these two methods for the 6-DOF case.However,this attempt is failed as the convex optimization-based method suffers from convergence issues. One potential reason can be identified. That is,the successive linearization process may result in large accumulation of errors for higher order system. Therefore, although obvious benefits can be obtained using convex optimizationbased methods, certain treatment regarding the convergence issue should be designed and future research can be carried out along this direction especially for high-order trajectory optimization problems.

Fig. 1 Position and Velocity Profiles: 3-DOF Model and 6-DOF Model.
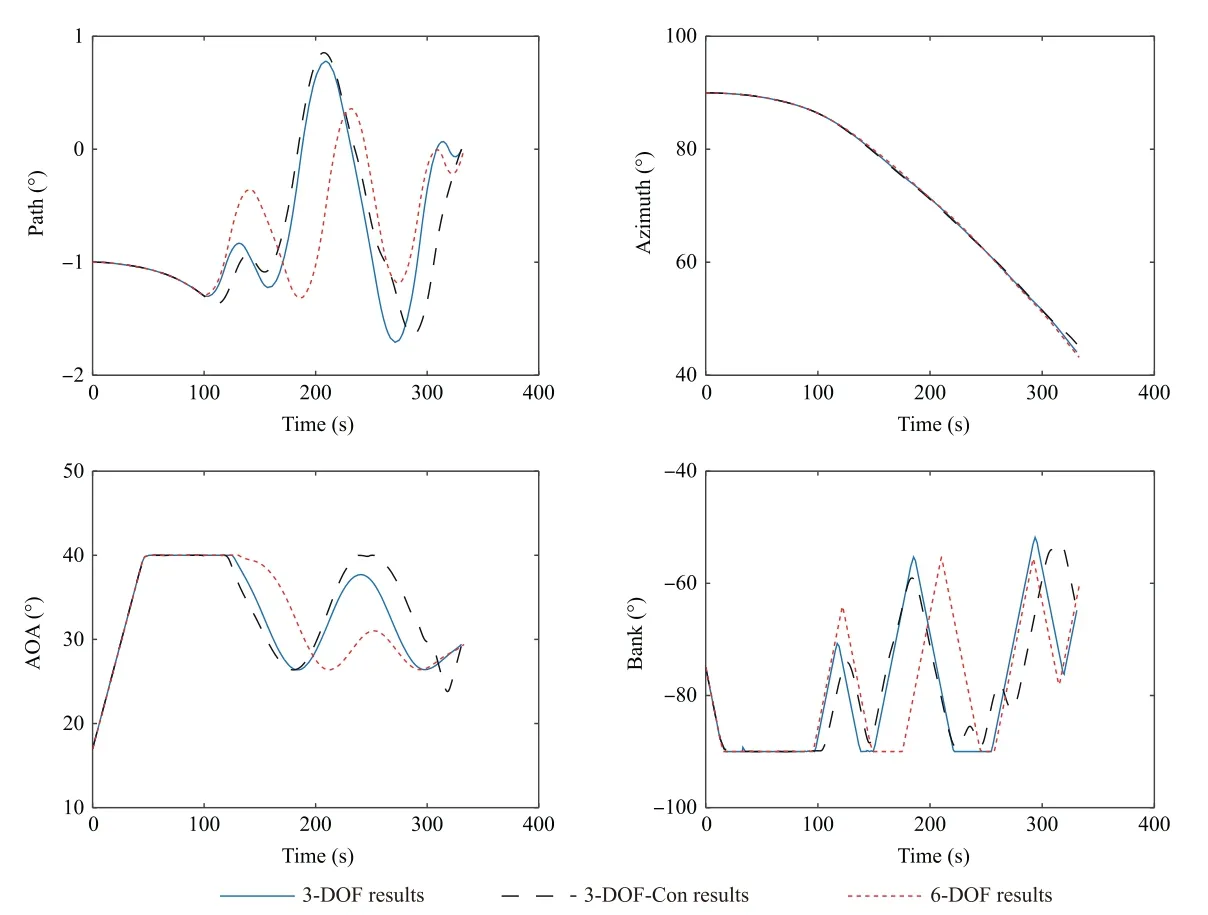
Fig. 2 Path, azimuth, AOA and bank angle profiles: 3-DOF model and 6-DOF model.

Fig. 3 Path constraint profiles: 3-DOF model and 6-DOF model.
4.3. Results with and without mesh adaptive process
In this subsection, the performance of the algorithm with and without the mesh adaptive process is further tested and analyzed. It should be noted that based on our experiments, a direct application of the pseudospectral method might encounter numerical difficulties for solving the 6-DOF reconnaissance trajectory optimization problem. To overcome this issue and improve the algorithm convergence, the pre-solve process introduced in Section 3 is applied on a small-scale temporal set. Subsequently, two test cases were performed with and without the mesh adaptive process introduced in Section 3 on the 6-DOF aeroassisted vehicle reconnaissance trajectory optimization model. The obtained results are presented in Fig. 6 to Fig. 10. Specifically, Fig. 6 and Fig. 7 illustrate the translational state profiles for the two cases, while Fig. 8 presents the corresponding constraint evolutions. In Fig. 9, the rotational state profiles are presented,whereas Fig.10 displays the optimized control moments for the two cases.
From the presented results, one thing needs to be highlighted is that the impose of heating and dynamic pressure constraints tends to prevent the vehicle from descending during the entire mission. That is, the aeroassisted vehicle has a hop at around 210 s in order to decrease the generated heat load and dynamic pressure, thereby protecting the structural integrity.
By comparing the results for the two cases, it is certainly true that the mesh adaptive process and a relatively-large set of mesh grid points are necessary for obtaining smooth and promising reconnaissance trajectories. This is more apparent for the rotational state variables shown in Fig. 9. Consequently,the advantages of applying the mesh adaptive process can be verified.

Fig. 5 Control moment profiles: 6-DOF model solutions.

Fig. 4 Angular rate profiles: 6-DOF model solutions.
4.4. Comparative results and analysis
In this subsection, we are interested in comparing the applied algorithm with other high precision pseudospectral-based methods existing in the literature such that the advantage of applying the decay rate-based mesh refinement strategy can be further appreciated. Specifically, the ph method suggested in Ref.30and the hp method reported in Ref.23are selected to form the comparative study.Early studies suggested that these two methods have the capability of producing high precision results for a wide range of aerospace-related trajectory optimization problems. By assigning the mesh adaptive tolerance values as ∊=(∊1,∊2,∊3,∊4)=(10-5,10-6,10-7,10-8), the comparative results were obtained. The results for different methods are displayed in Table 4, whereNadenotes the mesh adaptive iteration times,Nkindicates the total number of nodes among the final mesh grid, andtcreflects the computation time in second required for the algorithm. Note that in this table, the notation ‘‘-” indicates a failure (e.g., the algorithm fails to converge).

Fig. 6 Position and velocity profiles: With and without mesh updates.

Fig. 7 Path, azimuth, AOA and bank Angle profiles: With and without mesh updates.
From Table 4,we can notice that for the ∊1and ∊2cases,the ph method tends to have a relatively-large number of mesh iterations. Also, the computation time required for the ph method convergence is much greater than the others. Moreover, for tighter mesh adaptive tolerance cases (e.g., ∊3and∊4), the ph method even fails to converge. This can be explained by the fact that in the ph method, decreasing the polynomial error largely depends on enlarging the polynomial degrees.One main disadvantage of this strategy is that it might result in a slow decrease in the error and create a large number of unnecessary collocation points. Similarly, compared with the algorithm introduced in this paper, the hp method tends to consume more adaptive iterations and computation time to achieve the required mesh accuracy. This is obvious for∊1,∊2,and ∊3 cases.This is because in the hp method,the mesh adaptive process might add too many node points in a subinterval due to conservative estimation of the required polynomial degree. This will inevitably increase the time required for algorithm convergence or even result in a failure.

Fig.8 Path constraint profiles:With and without mesh updates.

Fig. 9 Angular rate profiles: With and without mesh updates.

Fig. 10 Control moment profiles: With and without mesh updates.
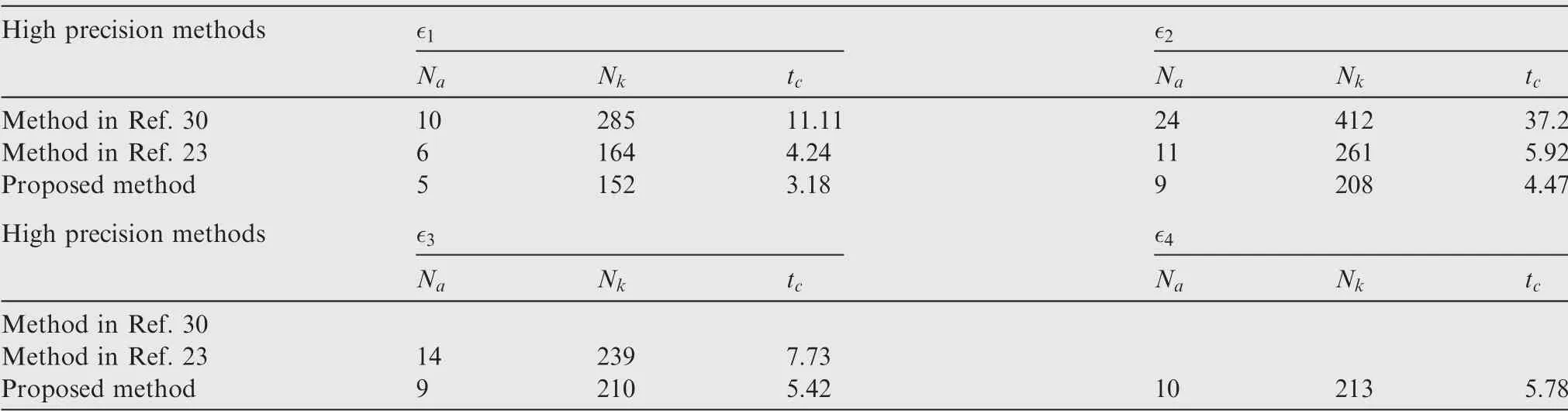
Table 4 Comparative results.

Fig. 11 Position and velocity profiles: Comparative study.

Fig. 12 Path, azimuth, AOA and bank angle profiles: Comparative study.

Table 5 Case specifications.

Fig. 13 Position and velocity profiles: Noise-perturbed cases.

Fig. 14 Path, azimuth, AOA and bank angle profiles: Noise-perturbed cases.
The trajectory profiles corresponding to the data reported in Table 4 are visualized. Specifically, position and velocity profiles are displayed in Fig. 11, whereas the path, azimuth,AOA and bank angle profiles are presented in Fig.12.By viewing the trajectory profiles presented in Fig.11 and Fig.12,it is obvious that the method introduced in this work can successfully converge to a solution for all pre-specified cases. The obtained trajectory profiles, together with the mesh and computational results provided in Table 4, confirm the effectiveness of the introduced method. Moreover, the enhanced computation performance of applying this method over other high precision methods can also be appreciated.

Fig. 15 Path constraint profiles: Noise-perturbed cases.

Fig. 16 Angular rate profiles: Noise-perturbed cases.

Fig. 17 Control moment profiles: Noise-perturbed cases.
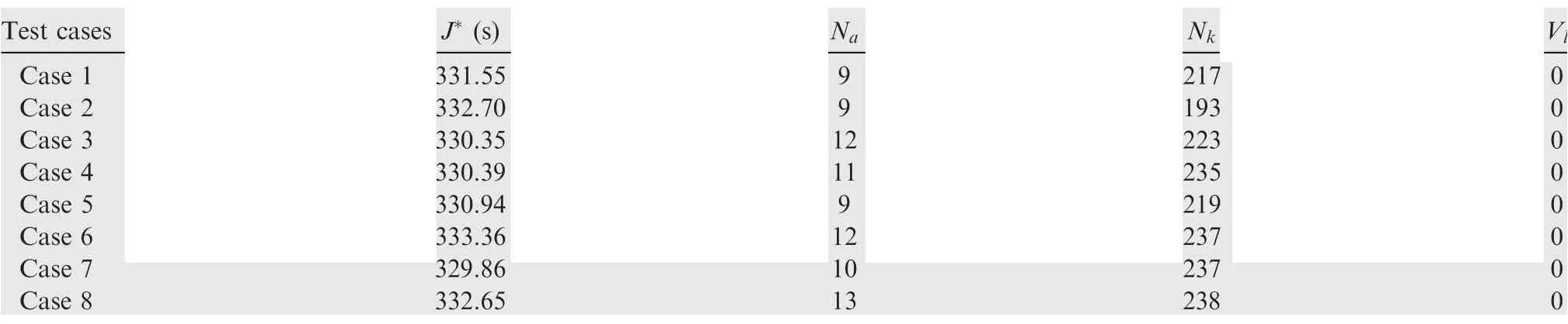
Table 6 Results of different cases.
4.5. Case studies with noise-perturbed initial conditions
In this subjection,case studies with noise-perturbed vehicle initial conditions were designed and performed to further validate the effectiveness and robustness of the applied method. Eight test cases were considered with perturbed initial conditions and their detailed settings are tabulated in Table 5. By applying the variable-order RPM method, the results for different cases are obtained and visualized in Fig. 13-17.
Apart from the optimized trajectories for different cases,detailed results are summarised in Table 6, whereJ*indicates the optimized final time value,NaandNkagain stand for the number of mesh adaptive iterations and the total number of the temporal nodes in the final adaptive iteration,respectively.Vldenotes the constraint violation value of the final solution.
From these presented trajectory profiles(e.g.,see Fig.13 to Fig. 17), one can find that the variation of initial conditions has an impact on the aeroassisted vehicle reconnaissance trajectory. However, all the cases can be successfully optimized via the variable-order RPM method. This can be reflected by the fact that the optimization process for all the test cases can successfully converge with the required accuracy tolerance satisfied and constraint violation nullified(see Table 6).Moreover, all the trajectory profiles are maintained relativelysmooth during the entire flying mission. This further confirms the effectiveness and robustness of the applied method for the considered problem.
5. Conclusions
In this work, we investigated and solved a high-fidelity reconnaissance trajectory optimization problem for aeroassisted vehicles using a variable order pseudospectral method. The formulated trajectory optimization model consists of both translational and rotational equations of motion,aerodynamic model, atmospheric model, and various constraints, thereby further narrowing the gap to the real system.A pipelined strategy based on a variable order Radau pseudospectral method was introduced to explore the optimal solution. After analyzing the simulation results, we found that:
(1) It is beneficial to include the both the translational and rotational dynamics in the trajectory planning phase,as the low-fidelity 3-DOF model might pose a potential safety concern.
(2) Direct application of the pseudospectral method might encounter numerical difficulties for solving the 6-DOF reconnaissance trajectory optimization problem. A potential recovery can be achieved by warmly start the optimization process on an initial small-scale mesh grid and gradually update the mesh grid to achieve the required accuracy level.
(3) The planned state and control trajectories tend to be smoother if the fixed mesh grid-based method can be replaced by the variable order strategy.
For future work, it would be worthwhile to devote efforts on addressing the convergence issue and improving the convergence rate of applying convex optimization-based trajectory design methods. This is of particular interest due to the fact that reduced computation time can be achieved by applying this type of approach (as indicated in Section 4.2). Besides,more sophistic and systematic design parameter selection strategy is desired such that the performance and convergence ability of the algorithm can be further enhanced.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Tangling and instability effect analysis of initial in-plane/out-of-plane angles on electrodynamic tether deployment under gravity gradient
- Aerodynamic periodicity of transient aerodynamic forces of flexible plunging airfoils
- Effects of swirl brake axial arrangement on the leakage performance and rotor stability of labyrinth seals
- Experimental and computational investigation of hybrid formation flight for aerodynamic gain at transonic speed
- Tomography-like flow visualization of a hypersonic inward-turning inlet
- Hypersonic reentry trajectory planning by using hybrid fractional-order particle swarm optimization and gravitational search algorithm
