Performance evaluation of complex systems using evidential reasoning approach with uncertain parameters
2021-03-16LeiyuCHENZhijieZHOUChnghuHURuihuYUEZhichoFENG
Leiyu CHEN,Zhijie ZHOU,*,Chnghu HU,Ruihu YUE,Zhicho FENG,b
aHigh-Tech Institute of Xi’an, Xi’an 710025, China
b Harbin Institute of Technology, Harbin 150001, China
KEYWORDS Complex systems;Evidential reasoning approach;Interval value;Performance evaluation;Uncertain parameters
Abstract The composition of the modern aerospace system becomes more and more complex.The performance degradation of any device in the system may cause it difficult for the whole system to keep normal working states.Therefore,it is essential to evaluate the performance of complex aerospace systems.In this paper,the performance evaluation of complex aerospace systems is regarded as a Multi-Attribute Decision Analysis (MADA) problem. Based on the structure and working principle of the system, a new Evidential Reasoning (ER) based approach with uncertain parameters is proposed to construct a nonlinear optimization model to evaluate the system performance.In the model,the interval form is used to express the uncertainty,such as error in testing data and inaccuracy in expert knowledge.In order to analyze the subsystems that have a great impact on the performance of the system, the sensitivity analysis of the evaluation result is carried out, and the corresponding maintenance strategy is proposed. For a type of Inertial Measurement Unit(IMU) used in a rocket, the proposed method is employed to evaluate its performance. Then,the parameter sensitivity of the evaluation result is analyzed,and the main factors affecting the performance of IMU are obtained. Finally, the comparative study shows the effectiveness of the proposed method.
1. Introduction
With the gradual expansion of modern aerospace systems, the complexity of the system and equipment is increasing.The performance degradation of each device may lead to the abnormal working of the system.In order to ensure the normal operation of the system,it is necessary to maintain good performance of all parts of the system equipment.For example,as a vital part of aircraft, the automatic flight control system is composed of altitude control system, speed control systems, lateral flight path control system,auto landing system, and so on. The performance degradation of any part will make the flight automatic control system difficult to meet the normal operating requirements. As such, the corresponding factors should be analyzed according to the evaluation result. In engineering practice, the testing data usually contain the system error and the random error. If there is malicious interference in the aerospace system, the testing data may have a large range of consistency deviation.1Taking the aerospace engine as an example, the working environment of the engine is characterized by strong noise, strong vibration, high pressure and high temperature, which will make the testing data inaccurate and unreliable. Therefore, how to use this information to evaluate the performance of the aerospace system to ensure its security and reliability is an urgent problem to be solved.
At present,there are many researches on the system performance evaluation.Qian et al.used the composite position process to establish the performance degradation model to evaluate the reliability of the platform inertial navigation system.2Chen et al. used the Analytic Hierarchy Process (AHP)to evaluate the performance of the system.3In order to evaluate the performance of the remote early warning system,Dong et al. proposed an evaluation method by combining the fuzzy model and the cloud model, which had certain practicability.4Wang and Feng made full use of historical data and presented a control system performance evaluation method based on rough set.5In order to deal with imprecise data and qualitative metrics, Lima-Junior and Carpinetti et al. presented a new approach to evaluate the performance of support supply chains.6For the problem of combination explosion in the performance evaluation of complex systems, a dynamic fault tree analysis method based on the idea of modularization was proposed.Dynamic fault tree approach can help to analyze system failures quantitatively and qualitatively.7However, the requirements of this approach for analysts’ knowledge are relatively high. If someone has not learned this approach adequately, it is hard for him to analyze the system failures.Aimed at the weaknesses of manufacturing execution system,Mo et al. established a general Petri net model to analyze the complexity, junction features and performance of the system.8However,if the system is quite complex,the model scale of Petri net may easily get very large, which makes it difficult to obtain the result.Based on the universal generating function and useful information,a novel technique for the performance analysis of a hydraulic system was presented to guide the system improvement in the design and operation phase.9The universal generating function can handle the uncertainty of systems. Nonetheless, it is necessary to know the probability density function of the variable when the function is used to analyze the system, and the probability density function of a variable is often difficult to obtain accurately in engineering practice. Yang et al. proposed a Binary Decision Diagram (BDD) based construction safety risk assessment method. The fault tree is transformed into BDD structure,and the key factors that affect the safety are obtained, which provides scientific basis for formulating safety risk control measures.10However, when the system complexity is high or the system scale is large, the scale of the decision diagram model constructed is also large and the computational complexity is high.
In recent years,some methods based on expert system have been developed and widely used. Zhou et al. proposed a performance evaluation method for network monitoring based on the separable temporal exponential random graph models,which was applicable to both independent and auto correlated networks.11Zhou et al.profiled the progress of the Belief Rule Base (BRB) model. Based on the expert system and evidence theory,BRB has been widely applied in complex industrial systems, like reliability evaluation, performance evaluation, fault diagnosis,and so on.12Since BRB can handle uncertainty and ambiguity,Feng developed a safety assessment model based on BRB to assess the safety of complex systems,which can ensure the interpretability of the assessment model.13With the increase of attribute dimension and referential values, the number of belief rules increases exponentially,which may lead to combinatorial explosion problem. Hence the combinatorial explosion problem of BRB needs further study. Mi et al. proposed an evidential network method for the reliability analysis and evaluation of complex multi-state systems that possess epistemic uncertainties.14
In the actual working process of aerospace systems, the operating environment is complex, and the system is often affected by various kinds of interference. The testing data often contain errors,which leads to the increase of uncertainty factors that affect the validity and accuracy of the data. It is difficult to deal with the uncertain factors effectively by using historical data,expert knowledge and working principle alone.Thus, it is necessary to make full use of all kinds of information to obtain the evaluation result in line with the actual working situation.The precise numerical value is often unable to capture the small dynamic changes under the complex working conditions, especially when the system is disturbed by various kinds of noises.The expression of interval threshold can combine the expert knowledge and the system operation state to select the data in the interval effectively, which can meet the actual requirements of the project. The performance evaluation of complex systems can be regarded as a kind of classification problem,which should obtain a preference result of evaluation according to some features or testing data of systems. Therefore, the system evaluation problem under the actual working condition can be transformed into the Multi-Attribute Decision Analysis (MADA) problem under the interval uncertainty. Multi-attribute refers to information or characteristics in many aspects. The Evidential Reasoning(ER) approach can make full use of quantitative data and qualitative knowledge to deal with the uncertainty. Therefore,the belief degrees of evaluation results in line with the actual engineering can be obtained.
Yang and Singh put forward the ER approach for the first time,and applied it to the performance evaluation of motorcycles, which provided a way to solve the Multi-Attribute Decision Making(MADM)problem effectively.15On this basis,Xu et al. put forward an extended ER algorithm, namely IER algorithm, which enabled the ER approach to deal with the interval uncertainty.16Wang et al. used the ER approach to model the new uncertainty such as interval data, and transformed the interval data into interval belief degrees equivalently.17
At present, the MADA based on ER is widely used in decision-making and evaluation problems.As a key parameter of the ER approach, the weight of evidence indicates the relative importance of evidence, which represents the degree of preference of decision-makers for evidence. Different decision-makers have different preferences for evidence,which can result in different evaluations.18-22It is necessary to consider the reliability of evidence in the ER approach.The reliability of evidence reflects the ability of evidence sources to provide effective information. Various kinds of noise and interference in evidence are often difficult to remove, which leads to uncertainties in the evidence reliability.23Compared with the precise numerical expression, the interval expression of reliability and weight is more suitable for engineering practice. In this paper, a new ER approach with uncertain parameters is proposed.The uncertainty of weight and reliability can be expressed in interval form. An ER nonlinear optimization model is constructed to achieve the parameter optimization.
The remaining parts of this paper are organized as follows.In Section 2, the problems are formulated. A new ER-based approach with uncertain parameters is proposed to solve the performance evaluation problem of complex systems in Section 3. A case study is conducted in Section 4 to verify the effectiveness of the proposed method. This paper is concluded in Section 5.
2. Problem formulation
The system structure and working principle of aerospace equipment are usually complex. Using ER approach to evaluate its performance can effectively deal with uncertain information including subjective uncertainties and objective uncertainties, so as to reduce the impact of uncertain factors on the evaluation result.At the same time,considering the performance of the internal structure of complex systems, it provides suggestions on making the maintenance strategy.Therefore, the following problems need to be solved:
Problem 1.Establishment of the evaluation index system
Complex systems are usually characterized by hybrid structure,multiple parameter indexes,complex coupling and correlation factors.The testing data are usually related to the whole system through each subsystem or intermediate equipment instead of being directly related to the overall performance of the system.24In the past, the ER approach was used to model and evaluate complex systems, which usually aggregated all the measurable indexes in the bottom layer to get the evaluation result of the system. This operation seems simple and direct,which yet ignores the state of each subsystem or equipment in the system.In the process of performance evaluation or fault diagnosis, it is necessary to master the working state of the subsystem.If the performance of some subsystems is difficult to meet the requirements of normal operation,fault location and maintenance shall be carried out.
Problem 2.Uncertainty of parameters
As for the MADA problem, due to the limited ability of human beings to understand things and the complexity of objective things, decision-makers are often unable to give the exact information of some attributes. All kinds of uncertain factors exist objectively in engineering practice. For example,the actual value of the size of a mechanical part varies within its tolerance zone, the elastic modulus and density of a metal material vary near an average value, and so on. Due to the sample representativeness,the accuracy and stability of testing equipment,and the objective existence of measurement errors,the point value form of parameters cannot be determined by the statistical analysis method,which may not fully reflect such complex properties as the variability and uncertainty. At present, the point value method is used to describe evidence weights and reliability in ER.However,due to the uncertainty in the initial data and the lack of data acquisition, the point value method is often difficult to accurately reflect the characteristics of the evaluated objection.In addition,the evaluation grade like poor, average,good or very good is usually a range rather than an exact point value.Therefore,how to reasonably express evidence parameters and fully express the uncertainty of information needs further study.
Problem 3.Sensitivity analysis of evaluation results
In engineering practice, the input information and the corresponding output information of complex systems are mainly used to establish the evaluation model, where the internal operation mechanism and state may be ignored. The system performance may be affected by a subsystem or specific equipment. It is necessary to determine the main subsystems that have the largest impact on the evaluation result. Based on the quantitative analysis, the performance of subsystems can be sorted.Then,decision-makers can take corresponding measures to improve the performance of those important subsystems, so as to provide useful information for the subsequent development of maintenance strategies.
To solve the above three problems, a performance evaluation approach for complex systems based on the ER approach with uncertain parameters is proposed.
3. ER-based approach with uncertain parameters for performance evaluation of complex systems
This paper tries to evaluate the performance of complex systems in aerospace equipment based on the ER approach with uncertain parameters. The proposed method can fuse multiinformation and reflect the performance of subsystems inside the complex system.Then,the sensitivity analysis of evaluation results can help decision-makers to draw up a maintenance strategy. The structure of the newly proposed ER-based approach is composed of three parts in Fig. 1.
Constructing evaluation indexes is the Part 1 according to system structure and operating principle. The Part 2 is the ER approach with uncertain parameters, which is involved in the uncertainty of input information. The Part 3 is the sensitivity analysis to obtain the importance order of inputs,which can provide maintenance strategies.The detailed strategies are introduced in the following subsections.
3.1. Performance evaluation index system of complex systems
In order to evaluate the performance of complex systems, it is necessary to divide the whole system into several independent subsystems based on the structure and operating principle of the system. If the subsystems are still relatively complex, they can be further divided into smaller parts until the indexes of smaller parts can be measured. According to the divided multi-layer subsystem,the evaluation index is constructed,and the ER approach is used to obtain the evaluation result from the bottom to up. The evaluation result of the lower indexes is taken as the evidence of the upper indexes, so that the evaluation result of the top index can be obtained. The evaluation indexes of the whole system are established in Fig. 2.
Considering that the actual system may be more complex,the system structure cannot be simply divided into several independent parts. There will be a coupling relationship between the indexes of each layer,which will affect each other.The evaluation method proposed in this paper is only applicable to the system that can be divided into structures as shown in Fig. 2.
Remark 1.If the systems cannot be divided into several independent parts,which means some parts are dependent,the method proposed in this paper should be revised. Yang and Xu defined an interdependence index in the evidence space to analyze the interrelationship between two pieces of evidence.And the interdependence index can be measured by marginal and joint likelihood functions.25Since the basic probability mass of evidence is generated based on the likelihood functions, the interdependence index may be used in the ER framework. The basic probability masses of several pieces of evidence are combined into the joint probability masses.In this way, the joint mass function may be applicable to solve this problem, and the detailed reasoning process under ER framework needs more in-depth research, which will be explored in the next work.
Fig.3 is an example of three-layer system structure used to illustrate the modeling process.The top-level index is the evaluation object, the middle layer is the subsystem, and the bottom layer is the measurable index.

Fig. 3 Performance index system of three-layer system.

Fig. 2 Performance index system of complex systems.
Since the bottom indexes are measurable, the evidence can be combined to obtain the evaluation result of the intermediate index.
Supposewiandriare the weight and reliability of evidenceeiamong the bottom indexes respectively.The belief degree βn,iis obtained by transforming the input information to thenth evaluation grade (n=1,2,...,N). The belief degree βn,1(m1)of intermediate indexm1is obtained by combininge1ande2.Similarly,e3ande4are combined to obtain the evaluation result βn,2(m2) of the intermediate indexm2.
After βn,1(m1) and βn,2(m2) are obtained, the intermediate indexes should be combined to obtain the evaluation result of the evaluation objectZ.The evaluation result of intermediate indexes is in the form of belief degree, and the weight and reliability should be calculated. In previous studies, Yang and Xu have proved that the maximum value of overall weight is 1,and the minimum value is the maximum value of each piece of evidence.26The overall weight is profiled by

wherewiis the weight of evidence, andwe(L)is the overall weight.
The overall reliability is the function of overall weight,which is given by

whereLis the amount of evidence;mP(Θ),e(L)is the residual support unassigned to any grade. The overall reliability is given by

According to Eqs. (2) and (3), the basic probability masses of the intermediate indexes are aggregated to obtain the evaluation result of the top-level index.

Since the reliability and weight are not precise values, the conventional ER approach is not applicable to obtain the final belief degree βn,1(Z).The ER approach with uncertain parameters can be used to solve this problem,which will be presented in the following subsection.
3.2. Combination of multiple interval belief structures using ER approach
In engineering practice, it is often difficult to get the exact value of some indexes. Also, it is easy to produce different kinds of errors in the testing process,which will result in uncertainties in the testing data. Since the testing data contain errors, they cannot be regard as true data, which may result in information uncertainties.In addition,some indexes cannot be measured with tools or equipment,and they usually need to be determined by expert knowledge. Due to the limited ability of human beings to understand things and the complexity of the objective things, decision-makers are often unable to give the exact value,which can generate the subjective uncertainty.
The interval value is superior to the traditional point value method,which is mainly reflected in the following aspects:the interval value is more reasonable and scientific than the point value in the expression of uncertain information, and it is in accord with the habit of expressing fuzzy information and the process of human brain thinking and reasoning.For example, when someone expresses the attribute classification of things, he is always used to adding ‘‘or so”, ‘‘about”, ‘‘more or less” and other fuzzy words that represent the range of the interval. When he makes the logical reasoning, the fluctuation range of things are always taken into consideration. In addition, the interval value is more accurate than the point value to express the degree of ownership of things, which can contain more information. Thus, the interval values can effectively reduce the error rate to ensure that the final decision is scientific and correct. Since all possible real values are contained in the operation result, the interval values are of great significance for practical applications. In engineering practice,due to the construction machinery and human factors, the parameters often have some errors. The parameters of ER are generally obtained through the data analysis and expert judgment.27Therefore, in the ER approach, interval parameters are used to evaluate the system performance instead of accurate parameters,which is more in line with the engineering characteristic.
The ER approach with reliability is presented briefly. Suppose there are two pieces of independent evidencese1ande2.The evaluation grades areH1andH2.e1ande2meet the following description:
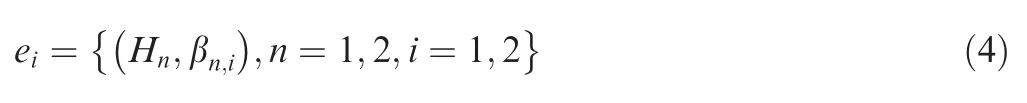
where βn,idenotes the belief degree of thenth consequentHnof theith piece of evidence.r1andr2are the evidence reliabilities.w1andw2denote the evidence weights.w~is the hybrid weight represented by

In the ER approach, the basic probability masses can be obtained by


Therefore,the belief degrees to the evaluation grades can be converted to the basic probability mass. After obtaining the interval basic probability mass, multiple basic probability masses can be combined by using the ER approach.
3.2.1. Combination of interval basic probability masses
The recursive combination ofLpieces of evidence using the ER approach is given by

It is necessary to optimize the evidence combination to obtain the optimal value range. If there are multiple pieces of evidence to be combined, the first piece of evidence and the second piece of evidence can be combined at first. Then,they can be combined with the third piece of evidence, and so on. When the final result is obtained, the overall optimization can be carried out. The upper and lower bounds of the final result can be obtained. Taking the combination of three pieces of evidencee1,e2ande3as an example, the basic probability masses are assigned asm1,m2andm3.m1andm2can be combined first, and the results can be then combined withm3.As such, the overall optimization can be conducted.
The combination ofm1andm2is given by

The result after the combination withm3is expressed as follows:

Under the constraint that the basic probability mass is an interval, the combination results are optimized and the value range of the basic probability mass is obtained. After optimization, the support degrees to each evaluation grade are obtained as follows:
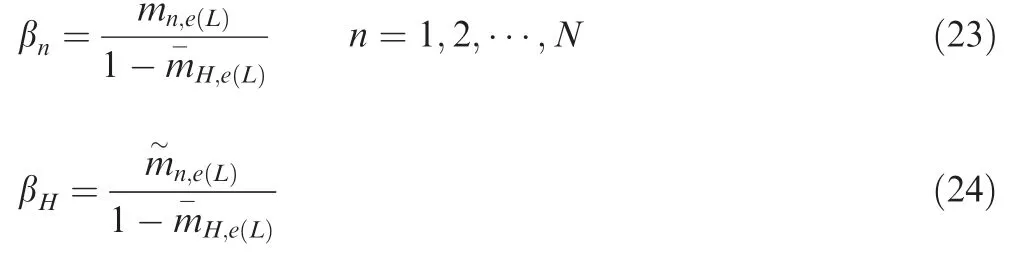
Based on the above calculations, the belief degrees to the corresponding grades are obtained.
Note that,when combining each piece of evidence and each part is optimized, and the optimal interval is used as the subsequent interval value, some wrong results may be generated.For the constrained optimization problem,the results obtained by optimizing each part are only the optimal solution in each part instead of the globally optimal solution. Therefore, all constraints and combination processes should be put in the same framework for overall optimization of the object,so that the result obtained can be guaranteed to be globally optimal.
3.2.2. ER nonlinear optimization model
Wang et al. pointed out that when the belief degrees of the original input information contained interval belief degrees,the calculation method of interval value could not be simply put into the ER, which would result in wrong results.28In order to correctly aggregate multiple interval belief degree, it is necessary to establish the ER nonlinear optimization model to optimize the belief degree of the whole evaluation object and obtain the belief degree to the corresponding evaluation grade.The optimization model proposed by Wang et al.28is shown below:


LINGO or MATLAB can be used to obtain the optimal interval value under the constraints. Based on the established ER nonlinear optimization model, the optimization results are the range of belief degrees to each evaluation grade.
3.2.3. Implementation steps of ER approach with uncertain parameters
According to the above analysis, the specific implementation steps of ER approach considering the uncertainty of evidence weight and reliability are as follows:
Step 1.Based on the error analysis and the relative importance of different evidence, the value ranges of evidence reliability and weight are obtained by the testing data and expert knowledge.
Step 2.The input information is transformed to belief degrees of evidence,and the interval values of basic probability masses are calculated.
Step 3.According to the reasoning process of the ER approach, all the evidence is combined.
Step 4.An ER nonlinear optimization model is established to optimize the combined results,and the belief degrees to each evaluation grade are obtained.
Thus, the procedure of the proposed method for modeling ER with uncertain parameters is shown in Fig. 4.
If the initial reliability, weight and belief degrees are point values, the above reasoning process is reduced to the general ER approach. The nonlinear optimization model is no longer needed to optimize the whole reasoning process.

Fig. 4 Flowchart of modeling ER with uncertain parameters.
3.3.Sensitively analysis of weight and reliability in ER approach
Sensitivity analysis is widely used to evaluate the effect of model parameters on model response in a small range.29In the ER approach, the reliability and weight of evidence have a great impact on the evaluation result.Quantitative sensitivity analysis of reliability and weight to the evaluation result will help decision-makers take targeted measures to improve the reliability and weight of evidence,so as to ensure the good performance of the system.
In this section, the sensitivity analysis process is described by taking the combination of two pieces of evidence as an example,and there are two output consequents.The reasoning process is conducted based on the ER recursive algorithm as follows:

Based on the ER approach, the sensitivity analysis of parameters to the evaluation result is developed.
3.3.1. Sensitively analysis of evidence reliability
The reliability of evidence is closely related to the ability of evidence source to provide correct information. When there is a deviation in the reliability of evidence, it will have a certain impact on the evaluation result.The influence of evidence reliability on the evaluation result will be analyzed,which is called the sensitivity analysis of reliability.30
In order to analyze the influence of evidence reliability on the result, it is necessary to take partial derivatives of reliability.31The detailed steps can be found in Appendix A.
By comparing the average sensitivity coefficientE(r) of each piece of evidence, the sensitivity of different evidence to the output belief degrees can be obtained.
Remark 2.Ifthe reliability of evidenceeiis more sensitive in the results than the reliability of evidenceej,which means that the change of the former has a greater impact on the result. If the information of evidenceeiis not accurate enough,the deviation of the result will be larger than other evidence. Therefore, in engineering practice, the priority should be given to take measures to improve the reliability or the measurement accuracy of evidenceei.
3.3.2. Sensitivity analysis of evidence weight
In the previous section,the sensitivity of evidence reliability to the result is analyzed, and the sensitivity coefficients of evidence reliability are obtained using the ER approach to combine different evidence. As the important parameters of ER approach,both the weight and reliability of evidence will have an impact on the result. By imitating the reliability sensitivity analysis method above, the influence of weight on the result can be obtained.
The detailed procedures are shown in Appendix B.By comparing the average sensitivity coefficientE(w)of each evidence,the sensitivity of different evidence to the output belief degrees can be obtained.
Remark 3.Ifit indicates that the weight of evidenceeiis more sensitive to the result than the weight of evidenceej, which means that the change of the former has a greater impact on the result.As the weight mainly depends on expert knowledge,higher requirements are put forward for the accuracy of expert knowledge. Therefore, in engineering practice, more experienced experts are needed to obtain more accurate evidence weights.
3.3.3.Comparison of weight and reliability sensitivity analysis of the same evidence
In the same piece of evidence,both the weight and the reliability will have an impact on the combination result.However,it is necessary to continue the sensitivity analysis to judge which parameter will have a greater impact on the result.
Both the weight and the reliability have an influence on the result through the hybrid weight. Therefore, it is essential to analyze which parameter is dominant. Similarly, the influence of the weight and the reliability on the hybrid weight can be calculated by the partial derivative method, shown as follows:

From Eqs. (42) and (43), as for the same evidence, which parameter has a greater impact on the result can be obtained by comparing (1-r) andw.
Remark 4.If (1-r)>w, the partial derivative of hybrid weight to the weight is larger, which indicates that the hybrid weight is more sensitive under the influence of the weight. In other words, if the weight and the reliability have the same magnitude of change, the hybrid weight influenced by weight has a larger change, which has a greater impact on the result.Therefore, the decision-makers should pay more attention to the relative importance of evidence or the accuracy of expert knowledge. If (1-r) Through the above analysis, it can be seen that if there is a deviation in the reliability or weight of evidence,it will have an impact on the evaluation result.31In engineering practice,there are certain errors in the monitoring data, and the reliability cannot be guaranteed. Using inaccurate reliability and weight values will increase the risk of abandoning actual data and taking false data, which will cause confusion to decision-makers and lead to wrong decisions. In order to prevent such cases in engineering practice, interval reliability and weight can be used to express the uncertainty of evidence,which can provide support for decision-makers,and reduce risk of making wrong decisions. Based on the above research work, the problems of uncertainty in the process of evaluation and optimization such as unreliable data and the inaccuracy of expert knowledge can be solved, and the range of evaluation results in accord with the engineering practice can be obtained. The practical application of this method will be studied next. In this section,an example of performance evaluation of Inertial Measurement Unit(IMU)used in a rocket is introduced to verify the effectiveness of the proposed method. As a vital component of the control system,the performance of IMU largely determines the working state of the control system. Once the performance of the IMU is abnormal, it can easily lead to the abnormal operation of the whole system and bring about irreversible loss. With a series of outstanding advantages such as high precision, rapid start-up, good temperature characteristics and environmental adaptability, this kind of IMU has been widely used in rockets, missiles, satellites, aircraft, ships,vehicles and other civil fields. Therefore, the performance of IMU should be evaluated. Based on its actual performance,the IMU needs to be repaired or replaced in time to ensure the control system in a good working condition. Both accelerometers and gyroscopes are important components of IMU. An accelerometer and gyroscope are installed in the positive and negative directions of theXYZaxis of IMU.According to the description in Section 3,an evaluation index system is established, as shown in Fig. 5. Since the same direction of gyroscope and accelerometer contains the same information, the difference method is adopted to process the cumulative pulse of each axis.The final indexes can be simplified into six ones, shown as Fig. 6. The data used in the research are collected by the technicians during the continuous test of the IMU used in a certain kind of equipment. However, there are some outliers in the data,and the amount of data is large. Hence, the outliers are eliminated. After eliminating outliers’ part randomly, the rest data are reordered according to the testing time. Thus, 96 sets of data can be obtained. Each set of data is six-dimensional,which represents the cumulative pulse of accelerometer and gyroscope in the three axes ofXYZrespectively. The first step of evaluation is to analyze the testing data.Evaluation information can be transformed into belief degrees using the rule or utility-based technique.32According to the distance-based reliability calculation method, the reliability of each index is calculated. The results are shown in Table 1.The coefficient of variation method is used to calculate the weight of each index. The results are shown as Fig. 7. The performance of the inertial navigation group should be measured by the navigation result. That is to say, the performance state of the IMU should be determined by the deviation value of the navigation result. According to the expert experience, three referential levels of Good (G), Average (A) and Poor (P) are set as grades for the performance, and the corresponding referential values of navigation deviation are 5 m,50 m and 200 m respectively. Based on the referential values of navigation accuracy, the referential grades and referential values of testing data of the gyroscope and accelerometer are calculated by combining relevant equipment information and expert knowledge, as shown in Table 2. According to the index system, the evaluation needs to be divided into three levels. The performance evaluation results of accelerometer and gyroscope are obtained by aggregating the bottom indexes. The obtained belief degrees are shown in Fig. 8 and Fig. 9. It can be seen from Figs. 8 and 9 that as for the gyroscope and accelerometer,the belief degrees of Average and Good are relatively higher during the measurement time. The belief degrees of Good decrease slightly in the later stage of the test. Based on the evaluation results of gyroscope and accelerometer, the performance evaluation results of the IMU can be obtained. Before calculating the overall evaluation result, the reliability and weight of gyroscope and accelerometer need to be obtained. According to the analysis in Section 3, the weight and reliability of gyroscope and accelerometer is interval threshold, which is obtained by Eqs.(1)-(3). The value range of weight and reliability is shown in Figs. 10 and 11. Fig. 5 Performance index of IMU. Fig. 6 New performance index of IMU. Fig. 7 Weight of each index. Table 2 Referential grades and values of IMU performance index. Fig. 8 Performance evaluation result of gyroscope. Fig. 9 Performance evaluation result of accelerometer. Fig. 10 Value range of reliability and weight of gyroscope. Fig. 11 Value range of reliability and weight of accelerometer. Fig. 12 Performance evaluation result of IMU. Under the constraint condition that the weight and reliability is interval threshold, the ER nonlinear optimization model is constructed to obtain the optimal range of the overall performance evaluation results for the IMU. The results are shown in Fig. 12. As can be seen from Fig.12,the performance evaluation of the IMU is obtained as the proportion of Good and Average,which accounts for the majority of the time.This indicates that it can maintain a good performance for most of the time. In the later stage of the test, the belief degree of Good tends to decrease slightly, while the belief degree of Average increases significantly.The belief degree of Poor begins to appear,which indicates that the performance of the IMU declines slightly in the later time. It shows an aggregated distribution assessment for each grade in Fig.12.In order to demonstrate the result more intuitively, the navigation deviation is calculated in the form of expected utility. Suppose that the distributed evaluation result can be represented by whereHndenotes the evaluation grade; βndenotes the belief degree ofHn;Nrepresents the number of evaluation grades. The calculation method of expected utility is defined by Note thatu(Hn) denotes the utility of gradeHn, and the utility interval of navigation deviation is shown in Fig. 13. As shown in Fig. 13, the changing trend is in accord with Fig. 12. The red line in Fig. 13 represents the utility range of performance evaluation results. The navigation deviation changes slightly most of the time. However, the curve trend increases gradually, which means that the performance of IMU becomes bad progressively. Thus, the IMU needs timely maintenance. According to the evaluation result of the IMU, the sensitivity analysis method in Section 3 is used for analysis. In the interval threshold of reliability and weight of gyroscope and accelerometer,a random value is selected as the reliability and weight value. Supposergandwgare the reliability and weight value of gyroscope respectively, andraandwaare the reliability and weight value of accelerometer respectively.The average sensitivity coefficients of reliability and weight are calculated by Eqs. (A21) and (B11). In order to reduce the error caused by random factors, the calculation process of average sensitivity coefficients is repeated for 100 times.Then, the average value of 100 groups of data is obtained as the final average sensitivity coefficient. The average sensitivity coefficients calculation results are shown in Fig. 14. It can be seen that the reliability of accelerometer is the most sensitive, followed by the reliability of gyroscope. The weight of gyroscope has the least sensitivity. Fig. 13 Performance evaluation result of IMU. Fig. 14 Average sensitivity coefficients of reliability and weight. Remark 5.As a representative of the importance of a piece of evidence, the weight reflects a decision-maker’s preferences over the evidence, which is subjective and depends on who makes the judgment. On the other hand, the reliability is used to measure the quality of a piece of evidence objectively,which is the inherent property of the information source where the evidence is generated. The reliability is independent of who may use the evidence. From the result of sensitivity analysis,the reliabilities of gyroscope and accelerometer are more sensitive than the weights. The reliability of accelerometer is more sensitive than that of gyroscope. On the whole, the reliability and weight of accelerometer are more sensitive than those of gyroscope. Consequently, compared with the performance of gyroscope, the performance of the accelerometer should be given priority under the same condition.At the same time,the reliability of accelerometer and gyroscope has a great impact on the result, which indicates that the accuracy of information provided by the evidence source is vital to the evaluation result. In engineering practice, some measures should be taken to improve the accuracy of data measurement and reduce the error on information acquisition. To compare with other methods, the initial ER approach, the Back Propagation(BP)neural network and the fuzzy inference method are used to evaluate the performance of the IMU with the same data.The initial ER approach is used to combine the six indexes in Fig. 6 directly to obtain the performance of the IMU after the testing data are transformed into belief degrees with the same referential values. The training data of BP neural network are half the number of the data, and the rest data are used for testing. In the fuzzy inference method, the index weights are the same as Fig. 6, and the matrix of fuzzy evaluation is the same as the belief degree of input information. In order to compare the evaluation results of several methods, the Root-Mean-Square Error (RMSE) of each method is calculated.The RMSE is used to measure the deviation of the observed value from the true value. Since the results obtained in this paper are interval values instead of precise values, it is difficult to compare the interval values with precise values.To solve this problem, the upper and lower bounds of RMSE are calculated. If the upper bound of RMSE is lower than that of the other methods,the proposed method can be proved of this superiority. The upper bound of RMSE reflects the maximal deviation of the interval value from the true value. There is always a point in the interval values that maximizes the distance from the real value every moment.Using these points to calculate the RMSE can obtain the maximal RMSE.Similarly,the lower bound of RMSE means the minimal deviation.Consequently, there will be a point in the interval values that will make the distance minimal. Based on the above analysis, the upper and lower bounds of RMSE can be obtained. Table 3 shows the RMSE of different evaluation methods.It can be seen from Table 3 that the initial ER approach has the greatest RMSE and is followed by the fuzzy inference method. The results obtained by BP neural network are more accurate than those obtained by fuzzy inference or initial ER approach.The upper bound of RMSE obtained by the method proposed in this paper is the least, which indicates the highest accuracy. The comparative results are shown in Fig. 15. In Fig. 15, the results obtained by BP neural network are not stable, and the results of the initial ER approach have the maximal navigation deviation.Compared with other methods, the method proposed in this paper has the highest accuracy, which validates its effectiveness in engineering practice. Table 3 Comparative studies with other methods. Fig. 15 Comparative evaluation results of IMU. In engineering practice, it is vital to monitoring the performance of complex systems. The main contributions of this paper are summarized as follows: (1) The multilayered evaluation index system of complex systems is established based on the system structure and working principle. (2) The ER approach is used to evaluate the performance of complex systems. To reduce the impact of error and interference in information or inaccuracy of expert knowledge, the evidence reliability and weight are profiled by interval threshold, which are in accord with the engineering practice.As such,the ER nonlinear optimization model is constructed and the system performance evaluation results are obtained. (3) The sensitivity analysis of evidence reliability and weight in the ER approach is conducted to obtain the performance of every subsystem or component.Also,it is used to figure out the primary factors that affect the performance evaluation result.Then,the maintenance strategy of the system in engineering practice can be provided to keep the system operating normally. In the following work, the method of how to obtain more accurate evidence needs to be studied to reduce the error of testing data and inaccuracy of expert knowledge. At the same time, the combination of dependent evidence needs further research. The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. This work was supported by the National Natural Science Foundation of China (Nos. 61773388, 61751304, 61833016,and 61702142),the Shaanxi Outstanding Youth Science Foundation (No. 2020JC-34), and the Key Research and Development Plan of Hainan (No. ZDYF2019007). Appendix A.The detailed steps of average sensitivity coefficients are shown as follows: According to Eq. (41), Eq. (A1) can be rewritten as where N and W are given by According to Eqs. (36)-(41),NandWcan be represented by Based on the reliability sensitivity analysis of the above two evidence combination,the sensitivity coefficients of the output belief degree of the combinedLpieces of evidence to the evidence reliability are obtained. Suppose ER model consists ofLevidences andNconsequents. The basic probability masses of evidences are profiled as Eqs. (6)-(9). The combined belief degree is obtained recursively by Eqs. (36)-(41). The sensitivity coefficients of thenth output belief degree to theith evidence reliability are obtained as follows: Based on Eqs. (6)-(9) and (36)-(41), the sensitivity coefficients of each intermediate parameter to reliability are calculated by Then the average sensitivity coefficients of evidenceeireliability are obtained by whereE(ri) is the average sensitivity coefficient of the output belief degrees to theith evidence reliability;Ldenotes the number of the evidences;Ndenotes the number of the evaluation grades. Appendix B.Calculation of the sensitivity coefficients for weight is shown as follows: Supposewi(0 ≤wi≤1) is the weight of evidenceeiwhich are not necessarily normalized. Since the influence of evidence reliability and weight on evidence is transmitted by the hybrid weight,when the first-order partial sensitivity calculation method is used to calculate the weight influence,only the partial derivative with respect to reliability is replaced by the partial derivative with respect to weight in Eqs. (A1)-(A8). The replaced ∂w~/∂wican be given by Suppose ER model consists ofLevidences andNconsequents. The basic probability masses of evidences are profiled as Eqs. (6)-(9). The combined belief degree is obtained recursively by Eqs. (36)-(40). The sensitivity coefficients of thenth output belief degree to theith evidence weight is obtained as follows: where Based on Eqs. (6)-(9) and (36)-(41), the sensitivity coefficients of each intermediate parameter to weight are calculated by Then the average sensitivity coefficients of evidenceeireliability are obtained by whereE(wi) is the average sensitivity coefficient of the output belief degrees to theith evidence weight;Ldenotes the number of the evidences;Ndenotes the number of the evaluation grades.4. Case study
4.1. Establishment of performance evaluation index system
4.2. Performance evaluation of IMU









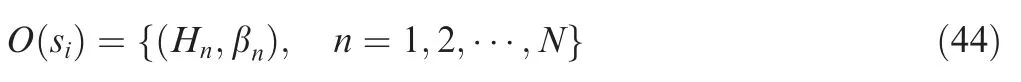

4.3. Analysis of experimental results



4.4. Comparison with other methods


5. Conclusions
Declaration of Competing Interest
Acknowledgments











杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Tangling and instability effect analysis of initial in-plane/out-of-plane angles on electrodynamic tether deployment under gravity gradient
- Aerodynamic periodicity of transient aerodynamic forces of flexible plunging airfoils
- Effects of swirl brake axial arrangement on the leakage performance and rotor stability of labyrinth seals
- Experimental and computational investigation of hybrid formation flight for aerodynamic gain at transonic speed
- Tomography-like flow visualization of a hypersonic inward-turning inlet
- Hypersonic reentry trajectory planning by using hybrid fractional-order particle swarm optimization and gravitational search algorithm
