Fast level-flight to hover mode transition and altitude control in tiltrotor’s landing operation
2021-03-16NingjunLIUZhihoCAIYingxunWANGJingZHAO
Ningjun LIU, Zhiho CAI, Yingxun WANG,*, Jing ZHAO
a Institute of Unmanned System, Beihang University, Beijing 100083, China
b School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China
KEYWORDS Tiltrotor;Transition;Flight control;VTOL;UAV;ADRC
Abstract An attempt is made to implement a faster level-flight to hover mode transition in tiltrotor’s landing process for the purpose of shortening its landing time. A three-stage tiltrotor landing maneuver is designed,and corresponding control modules and algorithms are created based on the analysis of the flight dynamics and the required actions of tiltrotor’s landing operation.As the altitude control is vital for tiltrotor’s near-ground landing, an Extended State Observer(ESO)control module of the Active Disturbance Rejection Control(ADRC)is designed to reduce altitude fluctuations in the fast mode transition, which makes the designed maneuver workable at very low altitudes. Simulations are conducted to verify the effectiveness of the designed maneuver and the validity of ESO control in various flight conditions. Flight test results that finally prove the effectiveness of the desired fast transition maneuver are reported.
1. Introduction
The tiltrotor is a relatively new type of Vertical Takeoff and Landing (VTOL) aircraft that can switch its configuration from a horizontal ‘‘level-flight” mode to a vertical ‘‘hover”mode, and vice versa. This allows it to possess the advantages of both the VTOL abilities of helicopters and the high speed,range, endurance and efficiency of fixed-wing aircrafts.1-3
In order to enhance the tiltrotor’s VTOL ability, it is of great importance to reduce the tiltrotor’s transition time from its level-flight mode to hover mode i.e. to realize a fast mode transition. On the one hand, this fast transition is directly required by many operations carried out by the tiltrotors,such as high agility flight,safe flight in battlefields,quick avoidance of obstacles, fast landings and so on. On the other hand, it helps to compensate for some of the ‘‘less optimized performances” of the tiltrotor. This is because most tiltrotors’mechanical structure and configuration are designed for optimized level-flight performance,such as maximum speed,cruise endurance,high efficiency etc.as tiltrotors usually spend much more time flying in the fixed-wing mode.4-6And this practice inevitability results in some less optimized or relatively poor flight performances when the tiltrotors fly either in or near the hover mode.7,8
The landing process is a typical tiltrotor operation that involves level-flight to hover mode transition.Actually it starts from the mode transition discussed above, and followed by a vertical descending process till tiltrotor finally touches down.Faster mode transition here means shorter landing time,which is of vital importance in certain tiltrotor operations,such as in military actions. To realize the fast mode transition in tiltrotor’s landing process, a three-stage tiltrotor landing maneuver is designed.In the first stage,the tiltrotor pitches up to increase angle of attack and drag,and the bank angle is used to control altitude. In the second stage a perching-like maneuver9,10is used to further decrease the tiltrotor’s speed, and in the final stage the tiltrotor returns to stationary hover in preparation for vertical descent and touchdown.For all stages,corresponding control modules and algorithms are designed and created based on the analysis of the flight dynamics and the required actions for each stage of tiltrotor’s landing process.
Altitude control is vital for the tiltrotor’s near-ground landing operations,in which modern control technique can play an important role. An Extended State Observer (ESO) control module of the Active Disturbance Rejection Control(ADRC)11is designed to reduce altitude fluctuation in the fast mode transition, and that allows the designed maneuver to be performed at low altitudes and in limited airspace.
Simulations are conducted to investigate the effectiveness of the designed fast transition in different flying conditions.Finally flight tests are performed to verify the results of theoretical analyses and the simulation work.
2. Tiltrotor flight dynamics and control system design
2.1. Subject tiltrotor
The subject tiltrotor used in this study is a tri-rotor UAV.The configuration layout is shown in Fig. 1.
The aircraft consists of a fuselage,main wings,two fore tiltable rotors,an aft fixed rotor,and a V-tail.All the rotor blades are assumed to have no flapping or lead-lag blade motion.There are eight controllable variables in all: deflections of the left and right elevons δeLand δeR,the deflection of the ailerons δa,the rotation speed each of the three rotors,and tilt angles of left and right rotors δtLand δtR. In this paper’s control algorithms δeLand δeRare converted to equivalent ‘‘elevator and rudder deflection” δeand δrvia Eq. (1):

The overall tilt angle δtis defined as δt= (δtL+ δtR)/2.When the aircraft is in the fixed-wing mode, δt=0°, and in the tri-rotor helicopter mode, δt=90°.

Fig. 1 Subject tiltrotor.
2.2. Dynamics model
The dynamics model is built using real aircraft parameters, as shown in Table 1. The model structure is shown in Fig. 2.
In this structure,the tiltrotor is divided into three parts and modelled separately:
(1) Gravity force.
(2) The fixed-wing part, which includes the fuselage, main wings, V-tail, and all control surfaces. Forces and moments produced in this part are mainly estimated using well-established methods.12,13Aerodynamic coefficients at high values of angle of attack α are obtained from relevant literature.14
(3) The rotor part, which includes the motors, rotors and tilt servos. The force and moment produced in this part are from rotor thrust. Rotor thrust at different inflow angles are estimated using an iterative algorithm15,16that combines actuator disk theory and blade element method.
Forces and moments from the above three parts are summed and fed into six-degrees-of-freedom equations of motion to calculate the tiltrotor’s motion states,such as angular velocity, position, etc.These motion states are then looped back to calculate forces and moments. In this way, a closedloop model is created.
2.3. Dynamics analysis
Three characteristics of the subject tiltrotor’s flight dynamics are important in the design of the quick level-flight to hover mode transition maneuver, and are discussed here:
(1) For the tiltrotor’s total lift force, it first increases with the increment of tiltrotor’s α,till α reaches its stall value αs. After that the lift force keeps dropping. To illustrate this,the calculated total lift force at airspeedV=15 m/s for different α is shown in Fig. 3.

Table 1 Aircraft parameters.

Fig. 2 Dynamics model structure.

Fig. 3 Lift force vs. α.
It can be seen after α>αs≈15°,the lift force decreases as α increases.This means at high values of α,the tiltrotor enters a post-stall flight state, and its wings will no longer be able to generate lift effectively.
(2) The drag force of the tiltrotor rises monotonically as α increases. This can be seen in Fig. 4, where the calculated drag force for different α atV=15 m/s is shown.
(3) At high speeds, it is very difficult for the tiltrotor to reach post-stall flight state(α>αs)by pitch-up increase.This can be seen from Fig. 5 (αM=0means α at whichM=0), which shows the calculated α at which the tiltrotor experiences zero total pitch momentM, with the maximum pitch-up input (via δeand difference between fore and aft rotor thrust).
It can be seen from Fig. 5 that whenVis greater than approx. 12.5 m/s, zeroMoccurs at α<17°≈αs, so the poststall flight is not reached.
2.4. Baseline altitude control
In the landing process, tiltrotor’s altitude control is vital for flight safety, and for this reason a baseline altitude control module is designed. The inputs for the module arezE(zcoordinate in earth frame),vEz(vertical speed), andzE,d(desired value ofzE). The output isaEz,d(desired vertical acceleration).
In this module, altitude control is achieved via a cascadedloop Proportional-Integral (PI) style controller. The desired vertical speedvEz,dis first determined fromzEerror:

In Eqs. (2) and (3)kP,zE,kP,vEzandkI,vEzare controller parameters.The outputaEz,dis used to calculate the bank angle φ in Section 3.2.1) and thrustupin Section 3.4.

Fig. 4 Drag force vs. α.

Fig. 5 αM=0 vs. V.
2.5. Baseline angular rate control
To control the attitude of the tiltrotor correctly,its body angular rates(roll ratep,pitch rateqand yaw rater)should be properly controlled. For this purpose, a baseline angular rate control module is designed. The input for the control module is the combined signal u=[pd,qd,rd,δt,up]T, in whichupstands for overall rotor thrust.The outputs are the control signals sent to the tiltrotor’s motors and control surface actuators.
In the control module, the desired body angular acceleration ˙pd, ˙qdand ˙rdare derived via feedforward-supplemented Proportional-Derivative (PD) control:

In Eq. (4), the controller parameterskP,p,kD,qetc. are designed and tuned using conventional methods in linear control system design.
The subject tiltrotor is almost symmetrical about thex-y,yzandx-zplanes in its body axes,and so its products of inertia(Jxy,Jyz,Jxz)are negligible. ˙pd, ˙qdand ˙rdare then first converted to corresponding fixed-wing control surface actuator outputs via a dynamic-inverse-style algorithm:

In Eq. (5)Jxx,Jyy,Jzzare moments of inertia,Lδa,Mδe,Nδrare the roll, pitch and yaw moment produced per unit control signal, andkroll,kpitch,kyaware coefficients gain-scheduled with reference to airspeedV.
After δa,out, δe,outand δr,outare obtained from Eq. (5), the output signals to the rotors’ motors are derived as follows.The roll, pitch and yaw moments that need to be produced by the rotors (Lrot,Mrot,Nrot) are calculated:

where δa,δeand δrstands for the real(aircraft’s actual)deflections of the control surfaces (this is different from δa,out, δe,outand δr,out, to take into account effects of deflection angle saturation,actuator dynamics,etc.).The outputs to the motors are then derived fromLrot,Mrot, andNrotvia mixing algorithms commonly used in multicopter control.
2.6. Overall control structure
The overall control structure of the designed fast mode transition for tiltrotor’s landing process is shown in Fig.6.Basically,it contains the above discussed baseline angular rate and altitude control modules and the control parts for a designed three-stage tiltrotor landing maneuver,which is fully discussed in Sections 3 and 4. In the diagram, each control module’s content-related subsections are marked, and so do the control algorithm-related math equations.
3. Fast mode transition maneuver design
3.1. Tiltrotor’s landing process analysis and maneuver design
The conventional landing process for a tiltrotor17is shown in Fig. 7.
It begins from a trimmed and straight-and-level flight at Point A. At Point B, the mode transition starts and δtis set to 90° till Point C. In this period, the airspeed of the tiltrotor keeps dropping due to drag. At Point C, the airspeed is low enough, and the tiltrotor enters a near-stationary hover state,so the vertical descending operation can be started till final touchdown.
The landing mode transition for a tiltrotor,if looking from an energy dissipating angle, can be understood as to bring down the tiltrotor’s kinetic energy to zero. Commonly used methods for aircraft kinetic energy dissipation are:
Method 1.Converting the aircraft’s kinetic energy to potential energy by increasing altitude.
Method 2.Reducing the kinetic energy input.
Method 3.Increasing aerodynamic drag.

Fig. 6 Overall control structure.
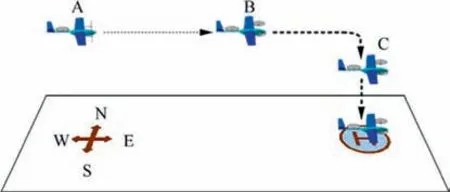
Fig. 7 Tiltrotor’s conventional landing process.
Method 1 is not suitable for this study,as the tiltrotor is in a landing i.e.altitude decreasing process.Method 2 is applicable in a tiltrotor by reducing the projection of thrust force vector on the direction of movement, or directing the tilt-able rotors’ thrust force away from the direction of flight. Method 3 can be applied by increasing the tiltrotor’s angle of attack,as it is discussed before and shown in Fig. 4, the drag on the wings and fuselage rises monotonically as the angle of attack α increases.
The combination of Methods 2 and 3 suggests the usage of a perching-like maneuver with δtset to 90° for the fast transition, as shown in Fig. 8. The idea is to implement large pitchup to make the tiltrotor enter high-α post-stall flight. As discussed in Section 2.3, in post-stall flight, the lift force keeps dropping,after α becomes larger than αs.And at the same time,a large α leads to a large drag.The thrust of the rotors at high α also points away from the movement direction.The ideal result of the above operation is: the tiltrotor’s airspeedVdecreases first, with its altitude increasing slightly due to the pitch-up motion. After that the altitude decreases slightly asVdrops.WhenVis low enough, the tiltrotor returns to level hover.
In practice however, this ‘‘perching” in tiltrotors is usually only applicable in mid-to-low speed flight. If this maneuver is attempted at highV, the tiltrotor’s α is not able to exceed αswith a large pitch-up input as discussed in Section 2.3, so that the desired post-stall flight cannot be achieved. The resulted behavior of the tiltrotor will like what is shown in Fig. 9. At first, the pitch angle θ increases, but α remains below stall value. This α combined with the effect of highVproduces a very large lift force, that makes the tiltrotor climb rapidly,and itsVdecrease as its altitude increases. Only afterVdrops to a suitable value, the tiltrotor enters post-stall flight. The overall effect is a quick increase in altitude,which is obviously not desirable for the transition in this study.
The problem is now focused on the altitude increase caused by large lift force.Since this lift force is inevitable if a large α is used to create the aerodynamic drag to realize fast mode transition,a method of directing the lift force sideways by banking the tiltrotor is designed.
In this banking way, the vertical projection of lift force (in the earth frame) is reduced, so as the tiltrotor’s tendency to climb suppressed.AfterVdrops to a suitable value for tiltrotor to enter the post-stall flight, the perching-like maneuver in Fig. 8 can be realized.
Based on above understanding and analyses, a three-stage tiltrotor landing maneuver is designed to realize the fast mode transition and is shown in Fig. 10. It still begins from a trimmed and straight-and-level flight at Point A like in the conventional transition,and at Point B,the three-stage maneuver starts:
Stage I(red dot line). At Point B, the tiltrotor’s δtis set to 90°.Immediately after Point B, at Point C, the tiltrotor banks and enters a turn. In this situation the tiltrotor’s vertical projection of lift force in the earth frame is directly related to bank angle φ,so φ is used to control the tiltrotor’s altitude.Pitch-up control is achieved by tracking a relatively large pitch rateq,while the pitch angle θ is set to zero. The yaw rateris set in conjunction withqto maintain zero θ. At Point D, the turn ends when the airspeed drops to a suitable value.
Stage II(green dot line).It starts as Point D.At Point E the tiltrotor returns to zero φ,and pitches up by tracking a large θ till Point F, when the tiltrotor enters into post-stall flight.
Stage III(blue dot line).At Point G,the tiltrotor’s speed is low enough, and it returns to hover state. The final vertical descending process is started till final touchdown.

Fig. 8 Perching-like maneuver.

Fig. 9 Actual response of the tiltrotor for a large pitch-up command input.

Fig. 10 Stages of fast transition maneuver.
3.2. Control module design in Stage I maneuver
3.2.1. Tiltrotor’s vertical acceleration control
Tracking the output of the baseline altitude control moduleaEz,dcorrectly is essential for altitude control. In Stage I,aEz,dis converted to φ.To derive the actual control algorithm,forces acting on the tiltrotor are first analyzed.
In the earth frame,the total force acting on the tiltrotor FEis as in Eq. (7):

In Eq. (7) Faero,Bis the total aerodynamic force in body frame, and LEBis the conversion matrix from body to earth frame. FE’sz-componentFEzaffects altitude, and is divided into 4 separate items in Eq. (8):

Item (a) to (d) are separately analyzed here:
Item (a): as θ ≈0,Faero,Bxsinθ is small numerically and is treated as a disturbance;
Item (b): as θ ≈0,Faero,Bysinφcosθ ≈Faero,Bysinφ. In the sharp turn maneuver in Stage I, φ is large and there will unavoidably be some side forceFaero,By, so this item cannot be neglected, and is treated as a disturbance;
Item (c): as θ ≈0,Faero,Bzcosφcosθ ≈Faero,Bzcosφ.Faero,Bzcan be roughly estimated from the on-board accelerometer,while φ is controllable, so this item is actively adjusted via φ to control altitude;
Item(d):it is assumed the estimated gravity of the aircraft ismestg, and contains uncertainties. The actual gravity ismg=mestg+Δmg, and the deviation in estimated gravity Δmgis treated as a disturbance.
From the above analysis, it can be seen that the vertical force can be approximately presented as:

where ΔFEzis the disturbance force.
From Eq. (8) andaEz=FEz/m, a direct relationship between φ andaEzcan be established:

In Eq. (9),Faero,Bz/mcan be roughly estimated by thezcomponent of on-board accelerometer measurementameas,z.The desired bank angle φdcan then be set as in Eq.(11)to control altitude.

φ is controlled by a proportional controller:

The conversion from ˙φ to body angular rates is:

From Eq. (12), the desired roll ratepdcan be calculated aspd= ˙φd- ˙ψdsinθ. Considering that θ ≈0 in Stage I, it is simply set as

pdis then inserted into u=[pd,qd,rd,δt,up]Tfor output to the baseline angular rate control module.
3.2.2. Tiltrotor’s load factor control
The tiltrotor’s load factornzis a measure of the stress to which its structure is subjected, and it is defined as the ratio of lift forceFliftto aircraft weightmg, i.e.

In the designed fast mode transition, especially in Stage I,the tiltrotor’s pitch-up motion results in a largeFlift, and that leads the increase ofnz. To limit structural stress to ensure flight safety, the tiltrotor’s pitch rateqshould be controlled such thatnzvalue do not exceed an up-limit value. For this purpose, the relationship betweennzandqneeds to be found out. In this process, the tiltrotor’s yaw rateris also derived from the control requirement of maintaining zero θ.
The pitch angle θ is controlled by a proportional controller:

Combine Eqs. (16) and (12) it can be derived that

The outputrdis set by Eq.(17)and inserted into the output signal u.
As θdis set to a fixed value 0, ˙θdis small numerically, and from Eq. (17)the approximate relationship betweenqandris then

From Eqs. (18) and (12) it can be derived that the heading angle change rate ˙ψ is

By combining Eqs. (18) and (19), it can be derived that

The angle of attack α in Stage I is not very large,and so the heading angle ψ is approximately equal to the direction the aircraft is moving.The centrifugal force acting on the aircraft can then be estimated as

The lift force,Fliftis related toFcenby the approximate relationship

By combining this with Eqs. (20) and (21), the relationship betweennzandqis finally established.

Based on Eq. (23), a load factor control module is added into stage I control block,for the purpose of limiting tiltrotor’s structural stress caused by the fast mode transition maneuver.In the module, the load factornzis set to a fixed valuenz,d, so that the output pitch rateqdvalue(used in the output u)is now decided by:

In the following simulation analyses and flight tests,nz,dwill be set to different values, so that the performances of tiltrotor subjected to different levels of structural stress can be compared.Hence the impact of differentnz,din designed fast mode transitions can be investigated.
3.3. Stage II control
In Stage II, the tiltrotor pitches up to enter post-stall flight by tracking a large fixed pitch angle θd. Generally, the altitude and airspeed in this stage should be close-loop controlled(as in Stages I and III). In practice however, the duration of Stage II is too short (usually only a few seconds, see simulation and flight test results) for closed-loop altitude and airspeed control to take significant effect. To correctly control altitude and airspeed, an open-loop control approach is applied, and ad hoc tuning used to determine the correct θdand thrustup.
The desired Euler angles φd, θdand ψdare set as:

The thrust is set toup=uper, and δtis set to 90°. θperanduperare fixed values, which are tuned such that the tiltrotor’s altitude changes little in Stage II.
The body angular ratespd,qdandrdare derived via Eqs.(25) and (12). They then used together with δtandupto form u=[pd,qd,rd, δt,up]Tfor output to the baseline angular rate control module.
3.4. Stage III control
In Stage III, the aircraft recovers from the large pitch-up orientation at the end of Stage II, and then simply hovers. The control algorithm is very similar to that in Stage II,except that rotor thrust is used to stabilize altitude. The desired Euler angles are:

From the values in Eq. (26)pd,qdandrdare derived and used in the output u.The thrust is set as in Eq.(27)to control altitude:

where ∂FEz/∂upis theFEzvertical force produced per unitup.δtis set to 90°.If horizontal position/velocity control is needed,φd, θdand ψdcan be set via conventional control methods in multicopter/helicopter control.
3.5. Transition between stages
The switching between Stage I,II and III depends on the measured airspeed. Two airspeeds needed to be decided are:
(1) VI→II:the airspeed at which to switch from Stage I to II,;
(2) VII→III: the airspeed at which to switch from Stage II to Stage III.
VI→IIis set approximately the maximum value ofVat which the tiltrotor can enter post-stall flight via pitch-up control. This is because α is much larger in Stage II’s post-stall flight than in Stage I. The deceleration in Stage II is therefore much faster, and it would be beneficial to transit from Stage I to Stage II as early as possible.VII→IIIis set via ad hoc tuning,and is adjusted such that at the start of Stage III,the tiltrotor’s speed is close to zero.
4. Application of ESO for altitude control
4.1. Problems in altitude control in tiltrotor’s landing process
In the tiltrotor’s landing process,the level-flight to hover flight mode transition should be conducted at low altitude for the purpose of shortening the time taken for aircraft’s final vertical descent and touchdown. It is then apparent that keeping altitude perturbations small is vital for flight safety during the near-ground flight mode transition (as shown in Fig. 11).
In the conventional landing process (as in Fig. 7) the altitude perturbations can be kept relatively small,as the tiltrotor is always flying near a trimmed and ‘‘straight-and-level” state in transition period.But for the fast mode transition proposed here, suppressing altitude perturbation is much more difficult for the following reasons:
(1) The tiltrotor experiences considerable aerodynamic disturbances (especially in Stage I, as explained in Section 3.2). These disturbances are largely related to flight parametersV, α and sideslip angle β. As α and β are not directly measureable, the disturbances cannot be directly calculated (e.g. from an explicit function f (V,α,β)), and have to be treated as unknown values;
(2) Theoretically, the above ‘‘unknown” disturbances can be cancelled out by integration or learning-based control methods such as adaptive control. However the actual‘‘fast transition” process takes only a few seconds, so the aerodynamic disturbances and altitude perturbations occur quickly and change fast. This leads to the ineffectiveness of the aforementioned integration or learningbased control.

Fig. 11 Transition with small and large altitude perturbations.
4.2.Application of active disturbance rejection control(ADRC)
It can be seen that much of the altitude control problems arise from the ‘‘unknown and fast-changing” nature of the aerodynamic disturbances in the fast transition. To overcome the problems, an Active Disturbance Rejection Control (ADRC)method11is introduced.
The ADRC is a relatively recent modern control method.As its name suggests, in ADRC disturbances are ‘‘actively rejected”. This is done by quickly estimating the total disturbance experienced from available sensor measurements at all times, and taking fast appropriate control action to cancel out these disturbances. In this way, ‘‘unknown and fastchanging” disturbances have little time to effectively change system states before they are actively suppressed.It can be seen that in ADRC,‘‘disturbance estimation”is the key to correctly rejecting disturbances. This action is performed in ADRC by the Extended State Observer(ESO)component,11,18,19and this component is used in this study for altitude disturbance rejection.
In the altitude control structure, the ESO acts as a supplement for the baseline altitude controller. Its output ΔaEz,dis added to that of the baseline altitude controller,aEz,d(as in Fig. 12). The ESO can be ‘‘switched off” via the ESO switch,by setting ΔaEz,d=0.The implementation of ESO is explained in detail as follows.
The output of the baseline altitude controlleraEz,d(as in Eq.(6)) can be understood as the vertical forceFEz,d(in earth frame) that the tiltrotor has to generate (either from bank angle in stage I or rotor thrust in stage III). When there is a disturbance forceFEz,distb, an additional vertical force ΔFEz,d≈-FEz,distbneeds to be added toFEz,dto cancel out effects ofFEz,distb.
The input of the ESO is expected vertical accelerationaEz,expandvEz.vEzcan be measured directly, whileaEz,expis

The ESO’s output is ΔaEz,d(this can be seen as the negative of vertical acceleration caused byFEz,distb), which is generated by the ESO system in Eq. (29) below:


Fig. 12 ESO in altitude control.

Fig. 13 Structure of ESO.
In Eq.(29),z3can be seen as the estimation of total disturbance.Therefore the ESO’s output ΔaEz,dis set as-z3to cancel out the disturbance. This ΔaEz,dis then added to the baseline altitude controller’s output. The structure of the ESO is as in Fig. 13.
In actual implementation, the parameters β02, β03, γ and δ are tuned.20
5. Simulation work and results
5.1. Simulation parameters
The important parameters to be set for the simulations are θper,uper(in Section 3.3),andVI→II,VII→III(in Section 3.5).They are set as follows:
(1) θperand uperare tuned to θper=57°and uper=0.4 respectively.
(2) VI→IIis set to 13 m/s.
(3) VII→IIIis tuned to 5 m/s.
The initial airspeed for all three transitions are set to 30 m/s,and initial altitude is set to zero for the purpose of displaying the altitude fluctuation clearly.
5.2. Effectiveness of designed fast mode transition
The purpose of the simulation here is to check the effectiveness of the designed fast mode transition applied in the tiltrotor’s landing process. In the work, a conventional mode transition is first analyzed in tiltrotor’s landing operation, followed by two fast mode transitions conducted with differentnz,drespectively and with the ESO (discussed in Section 4) turned off.
It needs to be noted that theoretically tiltrotor’s mode transition stops when the tiltrotor enters into ‘‘pure” hover mode.And in the proposed three-stage fast mode transition, that should happen at the end of Stage II. However in practice,for a smoother movement, the tiltrotor usually enters into Stage III i.e. the final vertical touchdown process before it totally enters into hover mode. This is whyVII→IIIis set to 5 m/s in Section 5.1. In the simulation, to fully display the tiltrotor’s performance in mode transition, the calculation and analyses are set to stop after the tiltrotor’s airspeed reaches near zero value (about 2-3 m/s). For the fast mode transition,this means the transition operation is extended to the beginning part of Stage III.
The airspeed changes for the three transitions are shown in Fig. 14. For two fast transitions, the curves of Stage I, II and III are shown in red, green and blue respectively.

Fig. 14 Airspeed changes during mode transition.
It can be seen from Fig. 14 that:
(1) The airspeed decreases slowly for the conventional transition,and reaches to near zero value in about 25 s. For the fast transition, the airspeed drops much faster, and reaches near-zero value in about 7-8 s. The result here is very inspiring and means the desired fast mode transition works.
(2) In fast transitions, the airspeed deceleration is rapider for load factor nz,d=3 compared with the result for nz,d=2. This is reasonable, as for bigger nz,d, the tiltrotor’s motion states are ‘‘allowed” to change faster, and that lead to rapider airspeed deceleration.
The horizontal trajectories for the three transitions are shown in Fig. 15.
It can be seen in Fig. 15 that:
(1) In the conventional transition, the tiltrotor travels east ward in a straight line for a very long distance.
(2) In the fast transitions,the tiltrotor’s trajectory is like the result of a continuous right turn.And the resulted circular like trajectory’s radius is about 24 m for nz,d=2,and about 16 m for nz,d=3. This means in the fast mode transition,the airspace needed by tiltrotor’s landing process is greatly reduced.This is another benefit and important improvement for tiltrotor’s landing operation.
(3) For the effect of different nz,d,the bigger nz,d=3 leads to a better result (16 m turn radius) than the result (24 m turn radius)for nz,d=2.This is consistent to the finding in airspeed changes in the fast mode transition.

Fig. 15 Horizontal trajectories during transition.
The pitch angle changes for the three transitions are shown in Fig. 16.
It can be seen that the pitch angle of the fast transition fornz,d=3 reaches about 42°, and fornz,d=2 reaches about 39°at the end of stage II. These mean the tiltrotor do enter into post-stall flight and prove the original design aim set in Section 3 is achieved.
Here again,the biggernz,dleads to a better result,as the tiltrotor enters into post-stall state in about 6.2 s fornz,d=3,while this value is 7.9 s fornz,d=2.
The altitude changes for the three transitions are shown in Fig. 17.
It can be seen from Fig. 17 above that:
(1) The altitude change for the conventional transition is relatively small, in the range of +0.5--0.8 m.
(2) The altitude changes for the fast transitions are greater.For nz,d=2 it is +0.6--1.2 m, while for nz,d=3 it is+0.7--1.8 m. This altitude fluctuation can be seen as the side effect of the fast mode transition. As discussed earlier, the altitude fluctuation in tiltrotor’s landing should be kept small. This is the reason of adding the ESO component into the altitude control to suppress the altitude change,and the related results are discussed in next subsection.
(3) For the effect of different nz,d,the situation here is different from the other results discussed above.As the bigger nz,dallows the tiltrotor’s motion states to change faster,a larger altitude fluctuation i.e. a larger side effect is resulted.

Fig. 16 Pitch angle during transition.

Fig. 17 Altitude change during the transition.
5.3. Effects of ESO application
The simulation here is to test the validity of ESO(discussed in Section 4) to control the tiltrotor’s altitude fluctuation. The altitude changes for the fast transitions with ESO off are displayed earlier in Fig. 18. Here they are plotted again with the comparison of the results of the fast transitions conducted with ESO turned on.
It can be seen from Fig. 18(a) fornz,d=2, and (b) fornz,d=3, that with the ESO turned on, the altitude fluctuation is suppressed to+0.6-(-0.7)m from the ESO off value+0.6-(-1.2)m, and to +0.7-(-1.3)m from +0.7-(-1.8)m. Hence the ESO suppression module takes effect.
6. Flight test results
6.1. Subject tiltrotor and parameters
The tiltrotor used in flight tests is a modified Nimbus VTOL RC model aircraft shown in Fig. 19. It consists a Pixhawk flight controller and related avionics. The flight control program is written using Pixhawk PX4 Support v2.1, provided by Mathworks. Aircraft parameters are shown in Table 1.
The other parameters needed by the control algorithm are the same as in the simulation work in Section 5.1, except for the initial airspeed. In flight tests, the landing operation command is manually issued by the RC operator. It is tried to limit the initial airspeed in the range of 20-30 m/s, and that differs from the accurate 30 m/s value used in the simulation.

Fig. 18 Altitude change for nz,d=2 and nz,d=3.

Fig. 19 Nimbus VTOL tiltrotor.
6.2. Effectiveness of designed fast mode transition
To confirm the simulation results discussed in Section 5.2, a flight test with the conventional mode transition implementation is first conducted, followed by flight tests with the fast mode transition implementation. In fast mode transitions,the ESO control module is turned off, and the targetnzis set to 2 and 3 respectively. The real-time airspeed changes measured via pitot tube are shown in Fig. 20.
It can be seen in Fig. 20 that
(1) The airspeed change pattern is very similar to the result in Fig.14.It shows that even though the initial airspeeds for fast mode transitions are greater(26 m/s nz,d=2 and 29 m/s for nz,d=3) than the initial airspeed for conventional mode transition (about 20 m/s), the times taken for the airspeed to change to zero are still reduced from 8.3 s to about 3 s.This means the conclusion made in the simulation work is confirmed, and the designed fast mode transition is finally proved working.
(2) Similar to the results in Fig. 14, a bigger nz,dresults in faster deceleration. The time taken for the airspeed to drop to zero is 2.5 s for nz,d=3, and about 3 s for nz,d=2.

Fig. 20 Airspeed changes during mode transition.
(3) It can be noticed that for both the conventional and fast mode transitions, the flight test results are better than the simulation ones. The times taken for the airspeed to change to zero for fast transitions are about 3 s in flight tests,but 7 ~8 s in simulations.The‘‘better”flight test performance here may not be bad, but it does indicate some kind of inaccuracies existing in tiltrotor’s dynamics model. More work needs to be done to improve dynamics model quality, especially in drag calculation.
The horizontal trajectories are shown in Fig. 21. It can be seen in Fig. 21 that:
(1) For both conventional and fast mode transitions, tiltrotor’s trajectories here are similar to the simulation results shown in Fig. 15, confirming the conclusion reached there. For fast mode transitions, again the airspace needed by tiltrotor’s landing process is greatly reduced.
(2) The load factor’s impact is larger. As in the situation of nz,d=3,the tiltrotor’s trajectory is not that circular-like,and more airspace is needed for tiltrotor’s landing process compared with the situation of nz,d=2.
The pitch angles for the transitions are shown in Fig. 22.
It can be seen that the pitch angle of the fast transition fornz,d=2 reaches about 43°, and fornz,d=3 reaches about 42°at the end of stage II.This confirms the tiltrotor does enter into post-stall flight.What are different from the simulation results are that, in real flights the pitch angles experience bigger fluctuations, especially in transition Stage I.

Fig. 21 Horizontal trajectory during transition.

Fig. 22 Pitch angle during transition.

Fig. 23 Altitude change during transition.
The altitude changes are shown in Fig. 23. It can be seen from Fig. 23 that:
(1) The altitude changes’pattern is like the simulation result shown in Fig. 17, showing the side effect of the fast mode transition.
(2) For the effect of different nz,d, again a bigger nz,dresults in larger altitude fluctuations.
(3) In the condition of real fights, the changes of the tiltrotor’s altitude are relatively smoother compared with the simulation results.
6.3. Effects of ESO application
In flight tests, the tiltrotor’s altitude fluctuation is not only caused by tiltrotor’s flight state change, but also affected by environment conditions, such as the strength and direction of wind. To better investigate the function of the designed ESO module, multiple flight tests are conducted, so that the statistical result of the tiltrotor’s altitude changes can be derived and analyzed.
Fornz,d=2, 23 fast mode transitions are performed with ESO off, and 15 transitions are conducted with ESO on. Fornz,d=3,5 transitions are performed with ESO off,and 6 transitions are conducted with ESO on. The altitude changes are shown in Fig. 24(a) and (b), in cyan and magenta separately.
It can be seen from Fig. 24 (a) that, fornz,d=2 with the ESO turned on, the altitude fluctuations are statistically suppressed to +5.5-(-3.5)m from the ESO off value +3.8-(-6.8)m.
While in Fig. 24 (b), fornz,d=3 with the ESO turned on,the altitude fluctuations are suppressed to +3.1-2.7 m from the ESO off value +2.9-7.8 m. Hence the results of the ESO suppression module obtained in simulation work are verified.
What is interesting here is: A biggernz,d, as discussed before, results a larger altitude fluctuation. However by comparing the results of Fig.24(a)and 24(b)here,it can be found that, in the situation of biggernz,d, the designed ESO module works more effectively.
6.4. Flight test videos
Videos of the flight tests can be found at
https://youtu.be/i13JR5UYPWo, and
https://www.bilibili.com/video/av82895650/.

Fig 24 Altitude changes for ESO off/on at nz,d=2, and nz,d=3.
7. Conclusions and future work
(1) A three-stage fixed-wing-to-hover mode transition maneuver is designed for tiltrotors with the goal of shortening their landing time. Dynamics models are built, related control modules and algorithms are designed to realize the fast transition.To reduce the altitude fluctuations in the transition process, an ESO is applied to the altitude control loop.Simulations are conducted to verify the effectiveness of the designed transition maneuver and the validity of ESO.Final flight tests confirm that the designed fast transition maneuver can effectively decrease tiltrotor’s landing time and the airspace required.
(2) The changeable flying mode is the most unique and important characteristic of a tiltrotor. To improve the flying quality of the tiltrotor, fast mode transition can play a great role. This fast nature of the transition first is directly needed by many tiltrotor’s operations, and then helps to improve other performances of the tiltrotor.More efforts should be put on the study of tiltrotor’s fast level-flight-hover mode transition, and vice versa,the hover to level-flight mode transition.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This study was co-supported by the Beijing Municipal Sci-Tech Program (No. Z181100003218015) and the Fundamental Research Funds for the Central Universities,China (No. YWF-20-BJ-J-542).
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Tangling and instability effect analysis of initial in-plane/out-of-plane angles on electrodynamic tether deployment under gravity gradient
- Aerodynamic periodicity of transient aerodynamic forces of flexible plunging airfoils
- Effects of swirl brake axial arrangement on the leakage performance and rotor stability of labyrinth seals
- Experimental and computational investigation of hybrid formation flight for aerodynamic gain at transonic speed
- Tomography-like flow visualization of a hypersonic inward-turning inlet
- Hypersonic reentry trajectory planning by using hybrid fractional-order particle swarm optimization and gravitational search algorithm
