基于思维导图的“线性代数”形象化教学探究

[摘 要] 利用思维导图把线性代数的抽象概念形象化。分别从行列式、向量组、零向量、秩及线性方程组出发，串联出线性代数各个章节的知识点，加深同学对线性代数抽象概念的理解并认识前后各个知识点之间的关联，培养学生解决复杂问题的综合能力和高级思维。

[关键词] 思维导图;线性代数;形象化教学

[中图分类号] G642.4   [文献标识码] A    [文章编号] 1674-9324（2021）01-0017-04   [收稿日期] 2020-03-10

线性代数是高等学校理、工、农、医、经、管等学科大学生的一门重要基础课程，也是后继相关课程和将来科技工作的数学基础。该课程包含了几何概念与代数方法的联系、严谨的逻辑推理、巧妙的归纳综合等数学思想，对于培养学生的数学素养具有重要的作用。随着计算机技术的飞速发展与广泛应用，作为离散化和数值计算理论基础的线性代数就显得日益重要。

线性代数的学习对象都是大学低年级学生，他们在学习线性代数的过程中极易掉进中学数学惯性思维的陷阱，对很多概念和运算很容易搞错、搞混淆。另外，抽象的概念、众多的公式及烦琐的运算使得线性代数课程成为学生学习中的“拦路虎”。所以，如何把线性代数的抽象概念形象化，是线性代数任课教师的首要任务[1]。

思维导图是20世纪70年代英国学者提出的一种表达发散性思维的有效图形思维工具，它既简单，又很有效，是一种实用性很强的思维工具。思维导图运用图文并重的技巧，充分运用左右脑的机能，利用记忆、阅读、思维的规律，协助人们在科学、逻辑与想象之间平衡发展，从而开启人类大脑的无限潜能[2]。

线性代数知识的思维导图是以某一个线性代数知识点为中心，将此知识点相关的定义、求法、性质、特点、关系、判定及应用等内容以图的形式展现，有效激发学生脑神经，促进学生记忆、理解、关联相关知识，达到对线性代数知识系统的整体把握[3]。

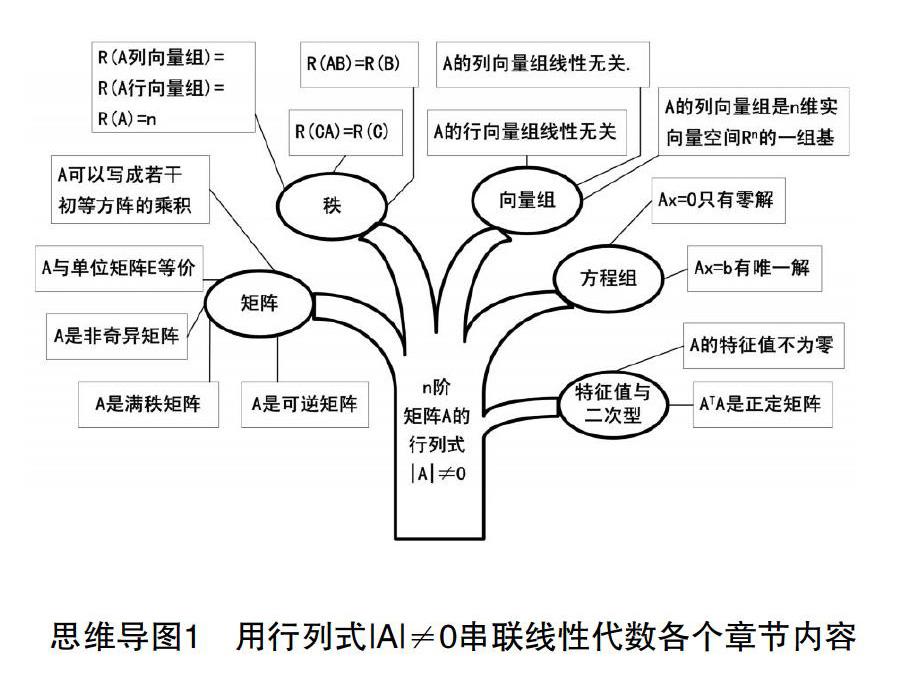
一、用行列式串联线性代数各个章节内容

行列式是大多线性教材的第一章内容，但它贯穿在线性代数的各个章节中，把线性代数各个章节内容之间的相互关系搞清楚是学好线性代数的关键。思维导图1和思维导图2分别从n阶行列式|A|不等于零和等于零两种情况出发，串联出线性代数各个章节所相关的知识点[4]。

二、零向量在线性代数章节中充当重要角色

零向量是一个非常特殊的向量，在向量组的线性相关性的定义、矩阵秩的计算、线性方程组、向量空间及特征值特征向量等知识中起到非常重要的作用。思维导图3分别从零向量的作用、特点、唯一性和“不能作为的角色”出发，阐述了零向量在线性代数知识体系中的重要性[4]。

三、用秩的概念来阐述线性代数各个章节内容

秩是线性代数知识体系中一个非常重要的概念，矩阵有秩，向量组有秩，二次型也有秩，它们之间既有区别又有联系，初学线性代数的同学往往对秩的概念理解不深刻，出现各种错误。思维导图4给出了矩阵秩、向量组秩及二次型秩的定义和求法;给出了矩阵秩和向量组秩之间的关系;给出了矩阵秩的含义;给出了利用秩判定线性方程组解的定理;给出了向量空间与秩的关系[5]。

四、用向量组的线性相关性串联线性代数各个章节内容

向量组的线性相关性是线性代数课程中的重点和难点，当很多同学学到这一概念时，就开始对线性代数课程产生了畏惧心理。在线性代数知识的学习中，不能完全独立地学习某一个知识点，而是应该把各个章节知识点联系起来学习，思维导图5从三个三维线性无关的列向量出发，串联出各个章节所相关的知识点;思维导图6从三个三维线性相关的列向量出发，串联出各个章节所相关的知识点[5]。

五、用齐次线性方程组解的情况串联线性代数各个章节内容

线性方程组是线性代数的核心，它是整个线性代数知识体系的主线。思维导图7从只有零解的齐次线性方程组出发，串联出线性代数各个章节所相关的知识点;思维导图8从有非零解的齐次线性方程组出发，串联出线性代数各个章节所相关的知识点[6]。

六、思维导图在教学中的应用

在2020年的疫情防控期间，全国各个高校都大力开展了网络教学，使得教师的教和学生的学在时间和空间上都发生了很大变化。在这种特殊情况下，利用思维导图开展教学，收到了非常好的教学效果。

首先，线性代数很多概念抽象难懂，教师把思维导图应用到线性代数课程的教学中，很好地实现了线性代数的形象化教学，增加了学生对概念的深入理解，搞清了各个概念间的逻辑关系，并有助于同学记忆相关知识，大大提高了教学质量，得到了同学的好评。

其次，线性代数课程有一个非常大的特点就是各个章节内容相互关联、相互渗透，教师把思维导图运用到线性代数各个章节的教学中，使学生掌握了各个章节知识点之间的关联，并且增强了知识点的趣味性，激发了学生的自主学习意识，大大加强了师生之间的沟通，提高了学生团结协作的学习能力。

最后，教师还应该引导和鼓励学生亲自动手制作线性代数各知识点的思维导图，进一步培养学生解决复杂问题的综合能力和高级思维。

参考文献

[1]杨威，高淑萍，陈怀琛，等.新工科背景下线性代数教学改革与探索[J].高教学刊，2020（5）：8-12.

[2]陈云辉，谢百治，赵丽.思维导图与学生创新思维能力培养[J].中国医学教育技术，2006（2）：10-12.

[3]杨鑫刚.思维导图在线性代数课堂教学中的应用[J].教育教学论坛，2018（14）：190-191.

[4]杨威.线性代数辅导讲义[M].北京：电子工业出版社，2011.

[5]杨威.线性代数名师笔记[M].西安：西安电子科技大学出版社，2014.

[6]陳怀琛，高淑萍，杨威.工程线性代数[M].北京：电子工业出版社，2007.