点阵结构填充模型的边界强化设计方法

任利民 戴 宁 程筱胜 龚 赛

南京航空航天大学机电学院，南京，210016

0 引言

增材制造技术的快速发展使得同时兼备超轻、高强等优异力学性能和降噪、散热等特殊性能的点阵结构迅速崛起[1]。点阵结构是由单个晶胞周期性阵列组成的多孔结构，在航空航天与国防工业、医疗器械行业、汽车制造业、建筑业[2-5]等都有着广阔的应用前景。

以前的研究主要集中在解决点阵结构力学性能不能充分发挥的问题上[6-10]，这些研究的优化域往往是点阵填充区，并未进一步考虑点阵结构与零部件之间的连接部分。点阵结构与零部件之间的连接部分往往承担载荷传递的关键作用。在基于点阵结构填充方式来实现零部件轻量化的设计中，较容易出现载荷并未有效传递至点阵结构内部、两者之间的连接部分却已发生界面剥离的破坏性失效，致使点阵填充区无法有效承载。界面剥离问题是限制点阵结构实际应用的主要瓶颈之一。因此，为使优化后的点阵结构在填充到零部件中时依然可充分发挥其改进的力学性能，需要首先确保载荷能够有效传递至点阵填充区。

目前，针对点阵结构与零部件牢固连接以减少边界处界面剥离问题的研究较少。WU等[11]指出，在点阵层与边界面层间添加铝制连接器可提高结构整体的协同变形能力，但这种方法仅适用于轧制点阵结构，不具备通用性。XIONG等[12]通过增加边界处连接面面积的方式提高了连接处的强度，虽然可以有效减少界面剥离问题的发生，但难以进行参数化调控、灵活性较差。PHAM等[13]、GUBICZA等[14]的研究指出，孪晶亚晶区、晶格析出及多晶格填充可阻碍边界处的位错滑移，同时边界处晶格方向的改变有效控制了剪切带的扩展，这种方法适用于点阵与点阵间交界处的界面强化而不适合工程应用。还有学者通过八叉树算法控制边界胞元尺寸，以提高边界连接处的强度。

本文提出一种面基参数化边界强化技术，实现连接牢固的“点阵-实体”优化模型设计，减少边界处界面剥离破坏性失效的发生，确保载荷从零件到点阵结构内部的有效传递。以连杆零件为例，在同等受力条件下，将优化模型与等体积的均质点阵结构模型进行对比来验证此方法的可行性和有效性。

1 边界强化模型

1.1 点阵结构数学表征

不同于传统CAD系统通过非均匀有理B样条表达模型，点阵模型用隐式距离函数表征。图1所示为基于线基元的距离场，线基元两端顶点分别为P1、P2，线基元上任意一点到模型表面的距离可表示为

D(t)=(R2-R1)t+R10≤t≤1

(1)

式中，R1、R2分别为线基元两端顶点P1、P2处节点值，即两端球形封头的半径；t为线段|P1P|长度与线基元|P1P2|长度的比值；P为线基元上任意一点。

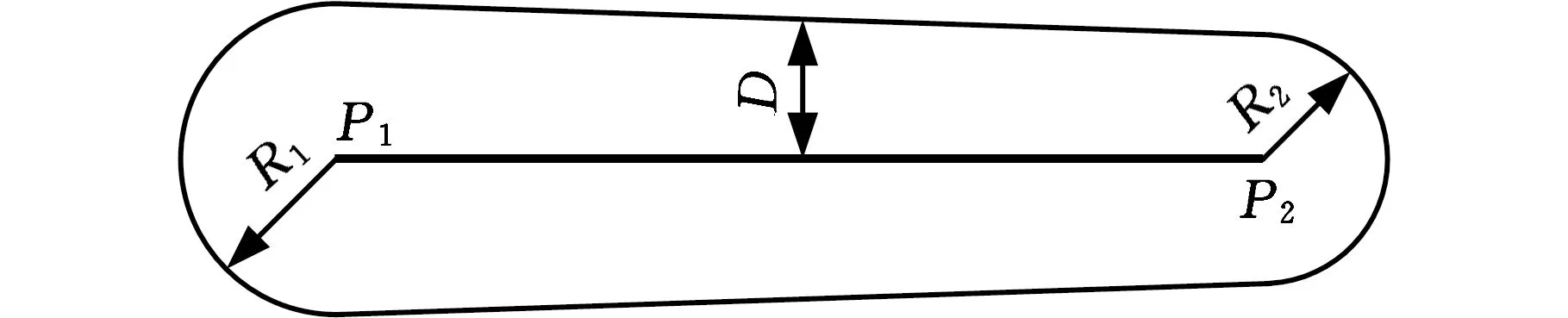
图1 基于线基元的距离场

假定点阵结构线基元集为l，则点阵结构的几何-拓扑关系可表示为

l=f(s,T,p,t0)

(2)

式中，参数s=S(a,b,c)控制胞元的尺寸；T控制胞元的类型；p控制点阵结构的位置分布；t0为容差参数，控制边界晶胞延展数量。

图2所示为基于线基元集的距离场，圆心位置和半径分别表示晶胞的节点坐标和节点值。

(a)节点值 (b)构建的距离场

构建的点阵结构模型可表示为

L=f(D(t),l,X)

(3)

式中，X表示采用的等值面抽取算法。

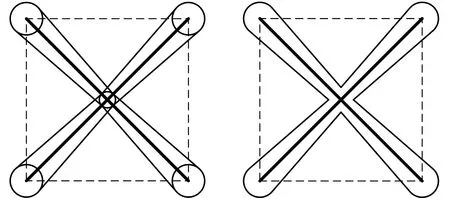
通过调控D(t)可较为灵活地参数化生成特定形貌的点阵结构模型，图3所示为不同距离函数类型经等值面抽取后得到的模型，图3a、图3b所示的重构模型采用式(1)构建，二者的区别在于线基元两端顶点处节点值是否相同。R1=R2时，重构模型为粗细相同的均一点阵模型，如图3a所示;R1≠R2时，重构模为变密度点阵模型，如图3b所示。图3c所示的重构模型采用二次距离函数D(t)=4(R1-R2)(t2-4t)+R1构建，此时R1对应线基元两端顶点处的节点值，R2对应线基元中点处的节点值，R1>R2。

(a)均一点阵模型 (b)变密度点阵模型(线性) (c)变密度点阵模型(二次)

本文采用式(1)中的线性距离函数构建模型，单个线基元构造的类胶囊状梁模型的体积计算可简化为

式中,Mkm为单位时间的最大含水量,h代表试样的厚度,为4 mm。M1和M2分别是时间t1和t2的含水量。由于所使用的样本的尺寸需要边缘校正,实际的样本扩散率可以被确定为:

(4)

式中，h为圆台的高度。

1.2 边界强化参数化调控

零部件与点阵结构交接处的体积存在跳跃式变化，交接处往往被视为脆弱风险区域，为保证载荷从零件到点阵结构内部的有效传递，使点阵填充区有效承载，在式(2)的基础上引入面基边界响应函数：

BFi=f(βti,βri,l)

(5)

式中，下标i表示第i个边界面；βti、βri分别为第i个边界面使用的基函数和边界影响因子；BFi的取值范围是0～1。

线基元节点值可通过线性插值的方式获取，插值函数为

Rpj=(C2-C1)Vpj+C1

(6)

式中，C1、C2分别为设定的节点值的下限和上限；Vpj为第i个边界面中的节点j的基边界响应函数BFi(j)。

如图4所示，给定单个边界面和线基元集，设置边界响应函数的基函数βt为线性函数，并给定边界影响因子βr。线基元集中的节点j与给定边界面的距离用dpj表示，则基于线性函数的单边界响应为

(7)

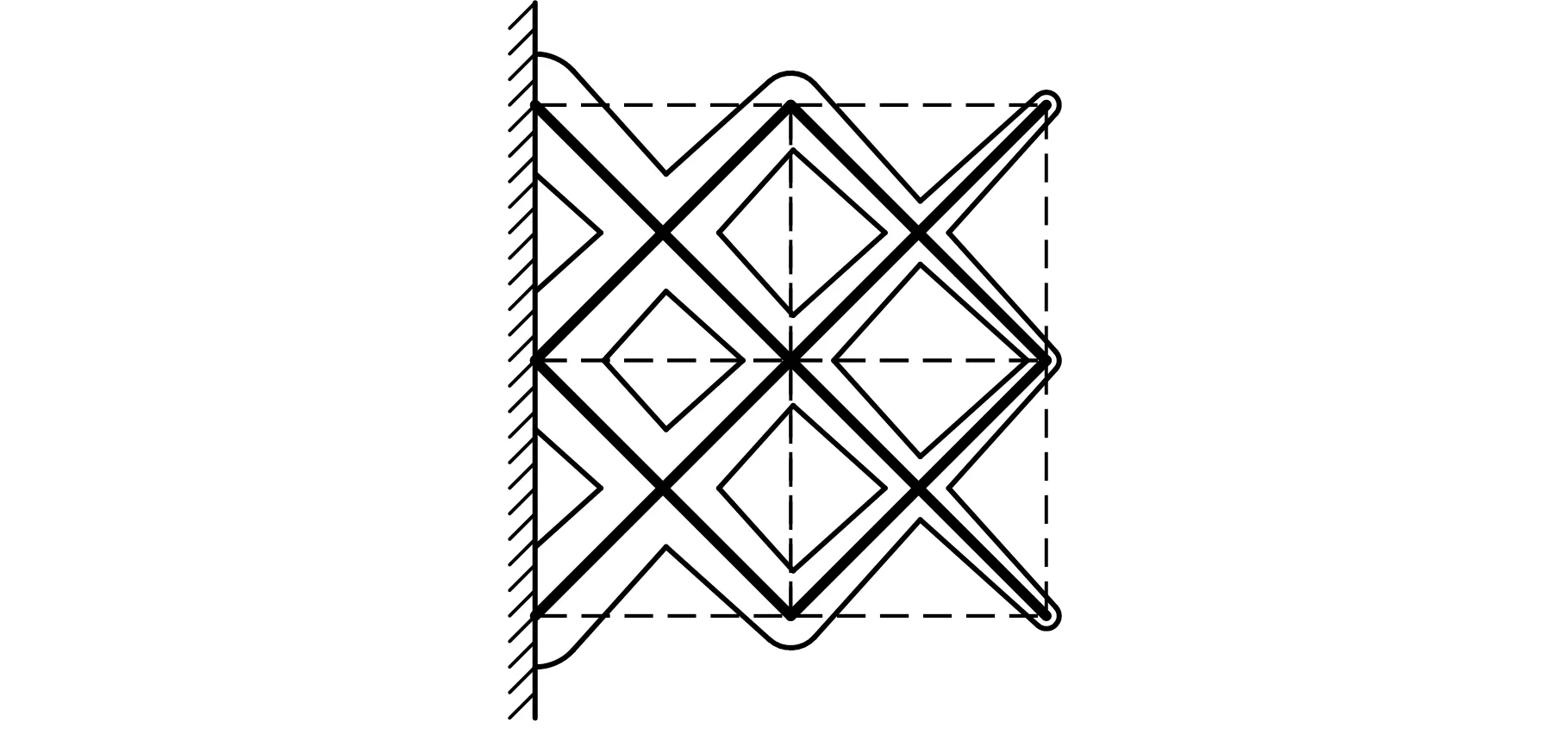
图4 基于线性函数的单边界响应

由式(7)可知，dpj越小，边界响应值Vpj越大。将边界响应值代入式(6)后，可得从近边界端到远边界端呈现出梯度变化的变密度边界增强点阵结构。

如图5所示，当有多个边界时，每个边界可指定不同的基函数和边界影响因子，最终的边界响应值由各边界响应值中的最大值决定，基于线性函数的多边界响应可表示为

(8)

式中，Vpji为第i个边界面的节点j的边界响应值。

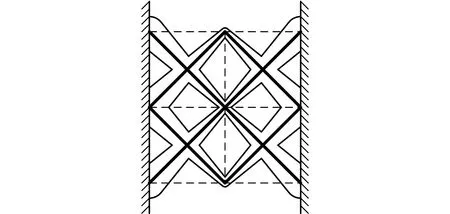
图5 基于线性函数的多边界响应

2 性能分析

为验证所提方法的有效性，以连杆零件为例，在保证相同体积的前提下，设计3组对照模型，通过物理压缩实验来比较边界强化模型与均质点阵结构模型。

各组边界强化模型设置的基函数、边界影响因子、节点值阈值及模型生成后的体积(由商业软件3-matic测得)见表1。为保证变量的唯一性，通过调控边界影响因子的大小来调整边界连接处点阵结构的体积梯度变化率，由图6可以看到，模型V1～V3的边界影响因子逐渐增大时，边界响应曲线斜率的绝对值越来越小，即体积梯度变化得越来越平缓。

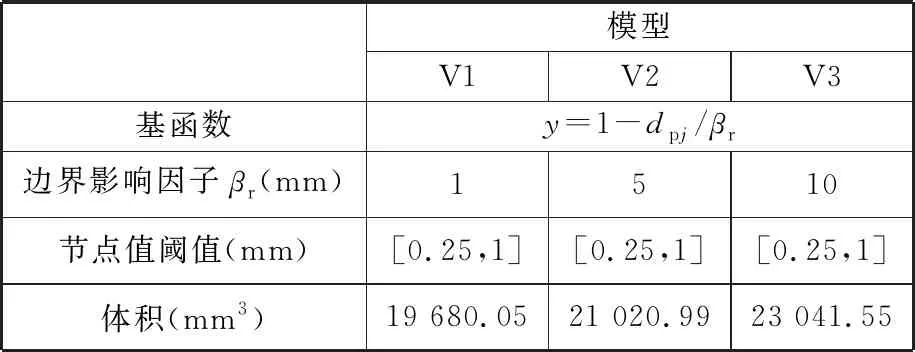
表1 边界强化模型数据

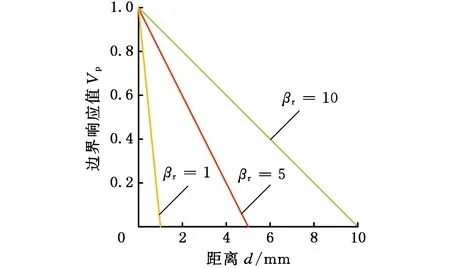
图6 体积梯度变化率的参数化调控

各组均质点阵结构模型的直径及体积(由商业软件3-matic测得)如表2所示。

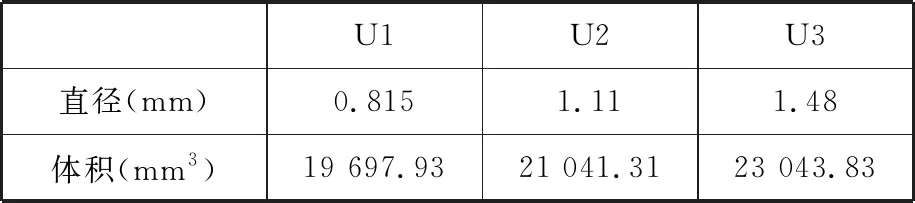
表2 均质点阵结构模型数据

构建的各个模型如图7所示，可以看到，模型V3在边界处的材料分布更加密集。

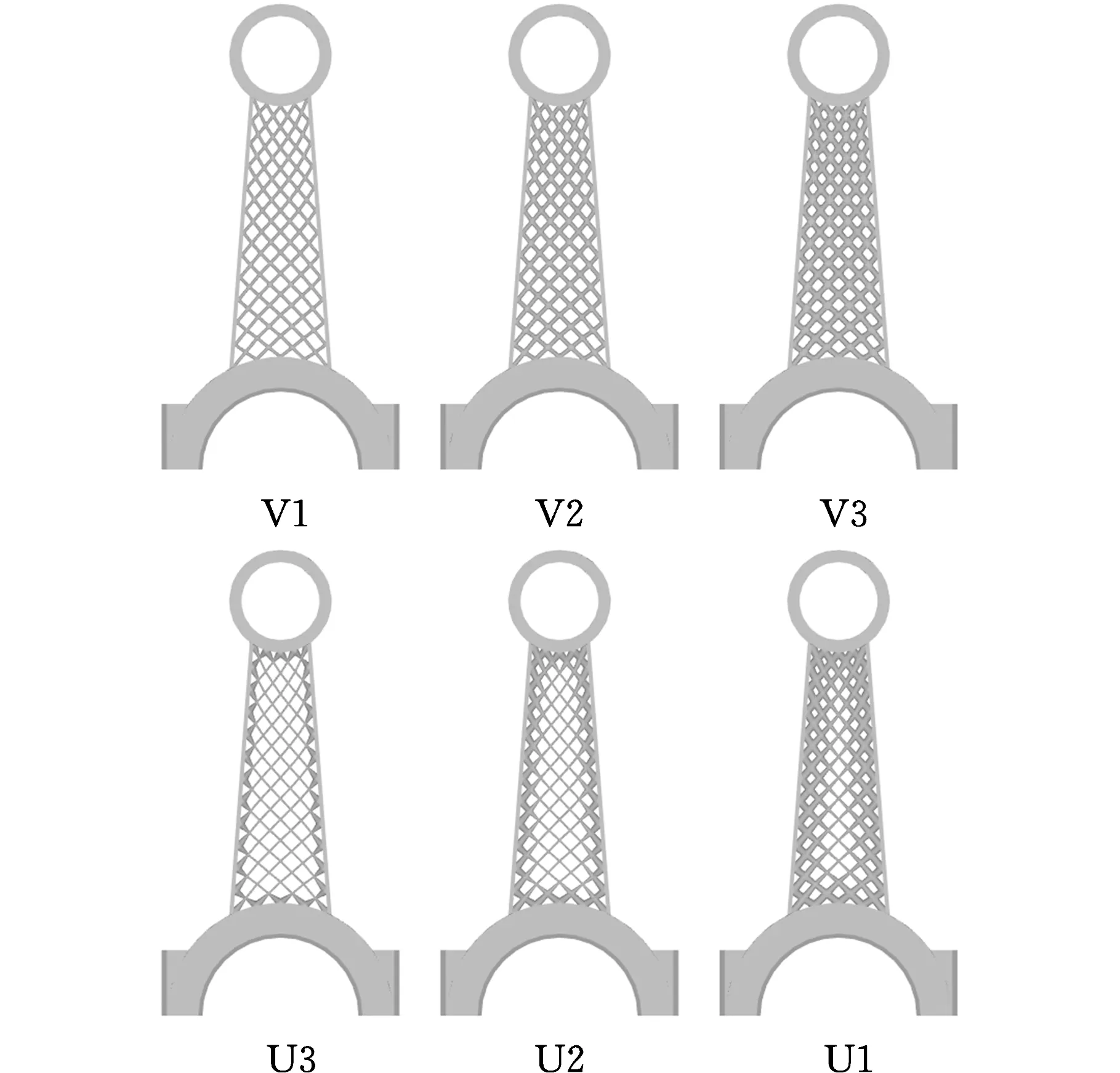
图7 边界强化模型与均质点阵结构模型示意图

2.1 物理实验分析

根据表1和表2中的数据，采用光敏树脂(C-UV 9400E)和光固化成形工艺制备模型样件(见图8)，样件质量见表3。

为表征各个模型样件的力学性能，本文以3 mm/min的速度在万能试验机WDW-E2000上对各模型样件进行单轴压缩实验，并记实验过程中的负荷、位移。样件的摆放及载荷施加位置如图9所示。

图8 SLA制备的模型样件

表3 模型质量

图9 模型样件单轴压缩实验

2.2 结果与讨论

2.2.1失效模式

图10所示的样件U1～U3的破坏失效表明，填充均质点阵结构零部件的失效形式具有较高的相似性：当承受外部载荷时，靠近固定端的点阵结构与模型样件之间的连接部分发生破坏性失效，即界面剥离破坏性失效，进而导致模型样件的完全失效，载荷并没有有效传递至点阵结构内部，点阵填充区不能有效承载。

(a)V1 (b)U1

图10所示的样件V1～V3的破坏失效表明，承载时，边界强化模型可较好地增大近模型外框边界处梁模型的强度，使点阵结构与模型样件之间的连接部分更加牢固，较好地解决了界面剥离问题。随着载荷的持续增大，载荷有效传递至点阵结构内部，点阵结构为主要的应力集中区。当点阵结构的强度不足以承担增大的载荷时，其内部发生不可逆的局部破坏性失效，载荷继续增大时，应力集中区由点阵结构内部转移至非点阵填充区，并在非点阵填充区发生断裂失效。样件V3的断裂失效发生在非点阵填充区的固定端圆环上，说明其填充的点阵结构相较于V1和V2有更高的强度，应力集中区已从点阵区域转移至非点阵填充区，模型样件外框在极限载荷下发生了断裂失效。

通过3组实验模型的横向对比可以发现：①较等体积的均质点阵结构模型，边界强化模型可确保载荷从零件到点阵结构内部的有效传递，使点阵填充区有效承载。②边界影响因子影响点阵填充区与非点阵填充区之间的体积梯度变化率，模型V1～V3点阵填充区的破坏失效为由近模型外框边界处梁模型破坏到模型外框边界处无梁模型破坏，说明随着边界影响因子的增大，体积梯度变化越来越平缓，点阵填充区的点阵结构与非点阵填充区的模型样件之间的连接不仅越来越牢固，而且模型样件的点阵填充区的承载能力也逐渐增加。边界影响因子很小即体积梯度变化很快时，点阵填充区的破坏失效呈现出更靠近于模型外框边界处梁模型破坏的趋势。当边界影响因子为零，即不进行任何强化处理时，破坏失效发生在与边界相连接的梁模型上，这与均质点阵结构的破坏失效高度吻合，即更容易出现界面剥离、点阵填充区无法有效承载。

2.2.2力学性能

通过物理实验得到的模型样件载荷-位移曲线见图11，边界强化模型的最大载荷大于等体积均质点阵结构模型的最大载荷。

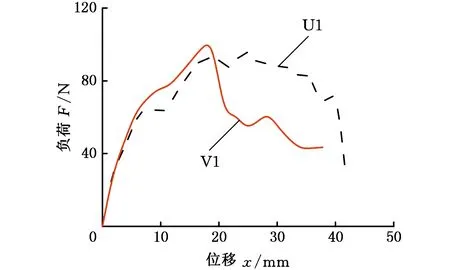
(a)U1-V1

图11中各组曲线表明，边界强化模型的承载变化与均质点阵结构模型不同。可以看到，随着压力机的不断下压，均质点阵结构模型U2和U3的载荷-位移曲线存在上升及迅速下降两部分，U1存在上升及缓慢下降两部分，U1～U3均只有一个转折点。边界强化模型V1和V2在受载时存在两个转折点，第一个转折点出现在载荷有效传递至点阵填充区后(内部点阵结构无法继续承受增大的载荷所致)，第二次转折点出现在应力集中区从点阵填充区转移至非点阵填充区后(零件外框无法继续承受所增大的载荷所致)。模型样件V3没有出现第一个转折点，说明载荷在有效传递至点阵填充区后，点阵结构内部承受了增大的载荷，应力集中区已经由点阵填充区转移至非点阵填充区。

模型样件U1与U2、U3的载荷-位移曲线有一定的差异，这是因为U1的杆径更小，点阵结构无法有效应对外载荷的增大。承受载荷时，样件U1发生弯曲变形，载荷主要由类悬臂梁状的模型外框承担，因而其载荷-位移曲线与悬臂梁承载时得到的曲线相似。受载期间，随着弯曲变形的逐渐增大，点阵填充区近边界处发生部分界面剥离，即部分破坏性失效，载荷-位移曲线由刚开始的逐渐上升变为逐渐下降，当类悬臂梁状的模型外框承受不住增大的载荷时，近固定端处发生破坏性失效。样件U2、U3的点阵填充区对类悬臂梁状的模型外框起到一定的支撑作用，即点阵填充区近边界处承力效果强于U1，受载时，其承力由模型外框与点阵结构共同承担，因此，载荷增大到受载极限后迅速减小。

样件V1～V3的最大载荷逐渐增大，说明随着边界影响因子的增大(体积梯度变化越来越平缓)，可适当提高承载能力。载荷-位移曲线中的拐点和样件的破坏失效表明载荷有效传递至点阵结构内部。值得注意的是，承载能力的提高是边界强化牢固连接点阵填充区与非点阵填充区和较高较应力区体积增大共同作用的结果。

综上所述，在相同制造工艺等条件的约束下，与等体积的均质点阵结构模型相比，本文提出的边界强化模型不仅提高了点阵结构与模型样件之间连接部分的强度，使得载荷可有效传递至点阵结构内部，而且适当提高了承载力。

3 结论

(1)通过参数化调控边界响应函数中的基函数和边界影响因子，可实现点阵填充模型由外到内、由密到稀的体积梯度式平缓过渡，提高了点阵模型的构建效率。

(2)面基参数化边界强化方法可使模型的点阵填充区与非点阵填充区之间构建起较为平缓的体积梯度过渡，有效降低点阵结构与模型之间连接部分发生界面剥离破坏性失效的风险，在保证牢固连接的同时，实现了点阵填充区的有效承载。

(3)在同等体积条件下，边界强化模型可适当提高点阵结构的承载能力，在保证有效传载的前提下进行点阵结构内部的二次尺寸优化，进一步提高其力学性能。