五轴加工中心旋转轴几何误差元素区别建模辨识技术
2021-03-15郑华林项锡平
郑华林 项锡平 胡 腾 米 良 刘 雁
1.西南石油大学机电工程学院,成都,610500
2.中国工程物理研究院机械制造工艺研究所,绵阳,621900
3.四川普什宁江机床有限公司,都江堰,611830
0 引言
五轴加工中心是航空航天、汽车和军事领域中使用最广泛的数字制造设备之一,其空间误差对加工精度有显著影响。现阶段,如何准确辨识旋转轴几何误差元素已成为机床空间误差建模过程中亟待解决的关键共性问题。
旋转轴几何误差元素定义方法[1]有绝对表示法和相对表示法两种。绝对表示法中定义了每根旋转轴4项位置无关几何误差元素(position-independent geometric error elements, PIGE)和6项位置相关几何误差元素(position-dependent geometric error elements, PDGE)。针对PIGE,IBARAKI等[2]提出相对表示法更有利于表示旋转轴之间的运动关系,如BC摆头转台型五轴加工中心,根据相对表示法可定义B轴2项PIGE,C轴6项PIGE。近年来,国内外学者提出了各种间接测量方法[2-6]来检测五轴加工中心精度。借助激光跟踪仪[5]提出通过点测量和位姿测量对刀尖点位置误差和刀轴姿态误差进行标定的方法,该方法需要采集大量数据点,适合大型数控机床。R-test测量仪[6]由于没有相关规范,故会因传感器的不同而导致测量算法和测量精度各有不同。球杆仪[2]由于测量方便、使用简单,被广泛应用于小型五轴加工中心旋转轴几何误差的测量与辨识。
基于球杆仪的旋转轴几何误差元素辨识方法有很多,XIANG等[7-8]提出了仅控制待测旋转轴运动的方法,通过规划球杆仪测量轨迹辨识了旋转轴8项PIGE和10项PDGE。郭世杰等[9-10]建立了基于圆轨迹的4种测量模式,辨识了两根旋转轴10项PIGE,提出了5次安装法,辨识了两根旋转轴12项PDGE。JIANG等[11]提出了两根旋转轴联动的测量轨迹,解决了两根旋转轴同时运动时合成速度与球杆仪采样频率间不同步的问题,辨识了旋转轴8项PIGE。以上研究方法在辨识过程中大多单独辨识这两种几何误差元素中的一种,缺少对PIGE与PDGE之间耦合作用的探讨。
目前,很少有研究注意到旋转轴PDGE建模方式与定义之间的联系。HUANG等[12]针对旋转轴误差定义模糊的问题,分析了“部件偏移”和“轴线偏移”两种旋转轴误差定义,对这两种误差进行建模与对比,采用球杆仪检测以验证误差模型的准确性。DING等[13]分析了旋转轴误差定义中两种不同的模型,即“error first”模型和“motion first”模型,根据“左基右一”原则,error first模型中误差元素定义在旋转轴理想坐标系下,motion first模型中误差元素定义在旋转轴实际坐标系下。付国强等[14]提出了六圈法,假设旋转轴零位置处6项PDGE为0,辨识出每根旋转轴10项几何误差元素。项四通[15]提出了迭代解耦的辨识方法,其中PIGE和PDGE都采用error first模型建模,辨识得到C轴PDGE。根据创成机理,PIGE主要是装配产生的误差[4,12,16],可以将PIGE理解为部件偏移,适合采用error first模型进行建模;PDGE主要是零部件制造产生的误差[4,12,16],可以将PDGE理解为轴线偏移,适合采用motion first模型进行建模。
不难看出,现阶段研究辨识的过程中大多单独辨识这两种几何误差元素中的一种或在建模时未考虑两类误差元素建模的差异性,由此可能导致旋转轴几何误差元素的完整性受到一定程度影响或无法体现几何误差元素本征属性等问题,不利于为机床精度反演提供理论与数据支持。为此,本文提出一种基于建模差异性的五轴加工中心旋转轴几何误差元素辨识方法,同时辨识旋转轴PIGE与PDGE。
1 旋转轴几何误差元素定义
1.1 五轴加工中心运动链分析
以某BC摆头转台型五轴加工中心为研究对象,其结构示意图见图1a。其中,OM是机床坐标系MCS(OMXYZ)原点,X、Y、Z轴行程分别为700 mm、400 mm、500 mm,B、C轴旋转运动角度范围分别为[-5°,115°]和[0°,360°]。根据多体系统理论,该机床运动学拓扑结构可分解为图1b所示的两个运动链,即刀具链(F-X-Z-Y-B-T)和工件链(F-C-W)。在金属切削过程中,切削成形点可以视为上述两运动链末端的交点。

(a)结构示意 (b)拓扑示意
1.2 旋转轴PIGE定义
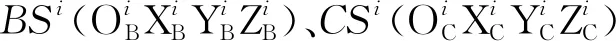

图2 基于相对表示法的旋转轴PIGE定义
1.3 旋转轴PDGE的定义
根据ISO 230-7,每个旋转轴的PDGE由6项参数组成。以C轴为例,如图3所示,PDGE包含的6项参数分别为δxC、δyC、δzC、εxC、εyC和εzC。其中,δ和ε分别代表线性误差元素和角度误差元素;下角标x、y和z代表C轴PDGE的误差方向。同理,B轴PDGE也可以采用类似的方式定义。

图3 C轴 PDGE的定义[1]
2 旋转轴几何误差元素辨识理论
2.1 旋转轴运动学建模
齐次坐标变换是构建五轴数控机床运动学模型的最常用方法之一[9, 14]。由于所有几何误差元素都可以视为名义运动以外的微小运动,因此两条运动链末端的最终位置可以表达为名义运动和误差微小运动的综合结果。
设EI,B、ED,B和EI,C、ED,C分别表示B轴和C轴的PIGE及PDGE,根据第1节中关于旋转轴几何误差元素的定义,有
(1)

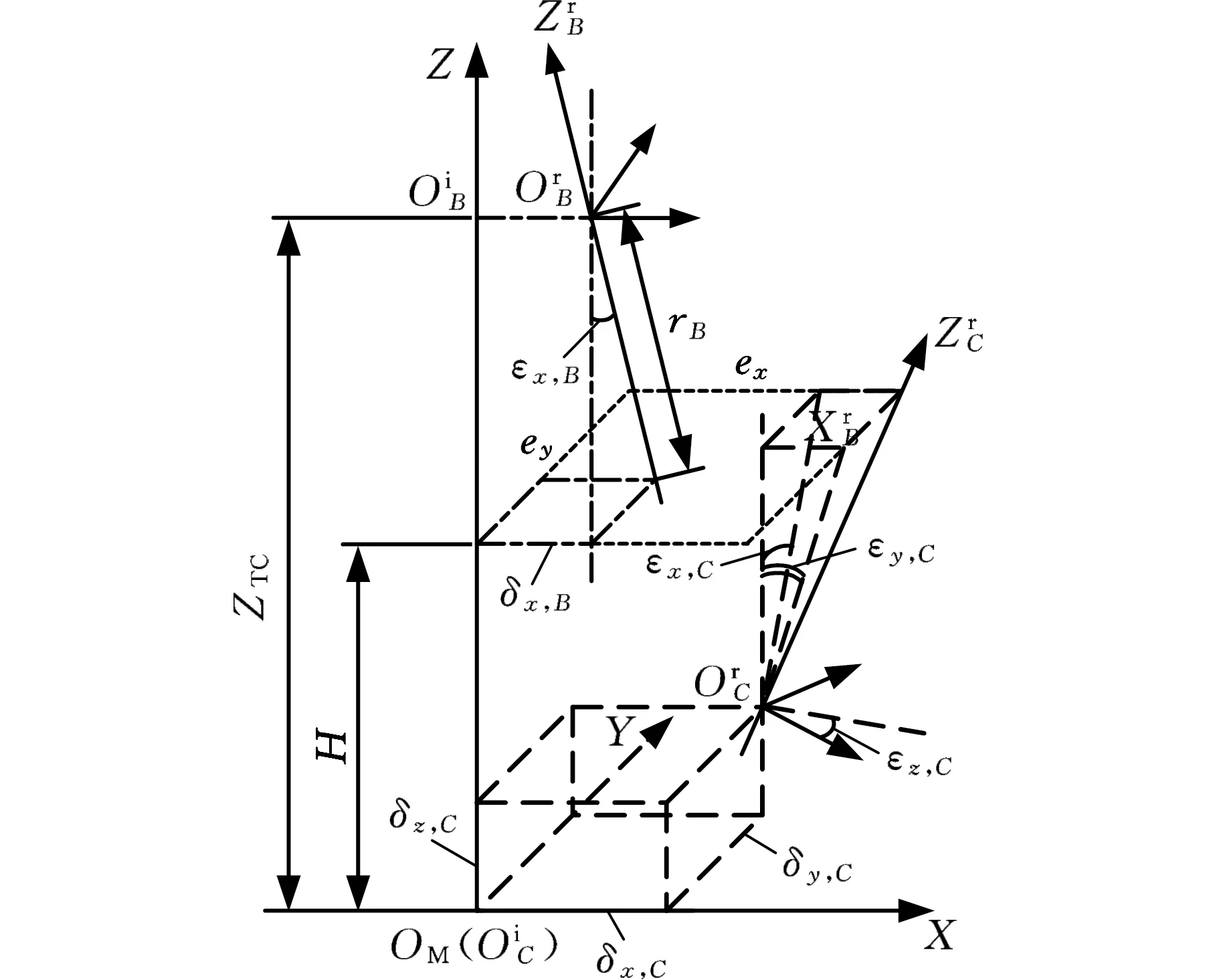
图4 两旋转轴初始位置关系
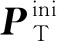
(2)
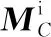
(3)
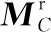
令li和lr分别等于机床两运动链末端PT和PW之间的初始距离和运动后最终距离,则两末端之间的距离变化量
(4)
值得说明的是,辨识基本方程组不包含B轴PDGE,其辨识方程亦可按上述方法推导构建。在旋转轴运动设计构思时,需在B轴旋转的同时确保C轴静止。由于篇幅限制,在此不再赘述。
2.2 Δl测量策略
为了辨识式(2)~(4)中PIGE和PDGE包含的14个几何误差元素,提出图5所示的三种测量策略[17-18]。其中,Owb与Otb分别代表球杆仪(名义长度l)两端小球的球心,下标wb、tb分别表示工件端小球、刀具端小球。根据测量过程中球杆仪轴线与Owb轨迹间的几何关系,三种测量策略被分别命名为径向、切向和轴向测量策略。
(a)径向测量策略 (b)切向测量策略 (c)轴向测量策略

(5)
(6)
利用CAM软件生成上述各测量策略的NC代码并运行,记录球杆仪所测的瞬时杆长变化量,亦即Owb与Otb间距离变化Δl,进而将测试数据代入式(4)。由于未知参数个数(待辨识的旋转轴几何误差元素个数)大于基本辨识方程个数,为避免出现静不定问题,须针对各测量策略设置不同安装参数(包括H和rC),以构建足够的辨识方程。
2.3 旋转轴几何误差元素辨识方法
2.3.1PIGE辨识方法
测量时,球杆仪杆长变化Δl由加工中心空间误差所致,而空间误差是机床直线轴、旋转轴几何误差元素综合作用的结果。五轴加工中心直线轴误差元素可利用激光干涉仪进行测量,预先通过NC代码补偿方式对直线轴几何误差进行控制,从而假定直线轴没有引入误差,此时Δl仅取决于旋转轴误差元素,即
Δl=ΔlEI,B+ΔlED,B+ΔlEI,C+ΔlED,C
(7)
式中,ΔlEI,B、ΔlED,B、ΔlEI,C和 ΔlED,C为球杆仪杆长变化分量,分别由EI,B、ED,B、EI,C和ED,C引起。
由辨识基本方程推导过程可知,ΔlED,B对Δl无贡献量(B轴保持静止),因此,图5所示各测量策略中,球杆仪Δl为
Δl=ΔlEI,B+ΔlEI,C+ΔlED,C
(8)
为辨识B轴PIGE,采用图5所示径向测量策略,并使工作台(C轴)保持静止,故ΔlED,C= 0,式(1)中ED,C可视为单位矩阵。此时,式(8)可进一步改写为
Δl=ΔlEI,B+ΔlEI,C
(9)
此时,Owb、Otb和OM之间的几何和运动学关系如图6所示。省略测量结果的二次项,长度分量ΔlEI,B和ΔlEI,C分别为
(10)
其中,ex和ey可由加工中心CNC系统读取。将式(10)代入式(9),有
Δl=(δx,B-ex)cosθ+(rBεx,B-ey)sinθ
(11)
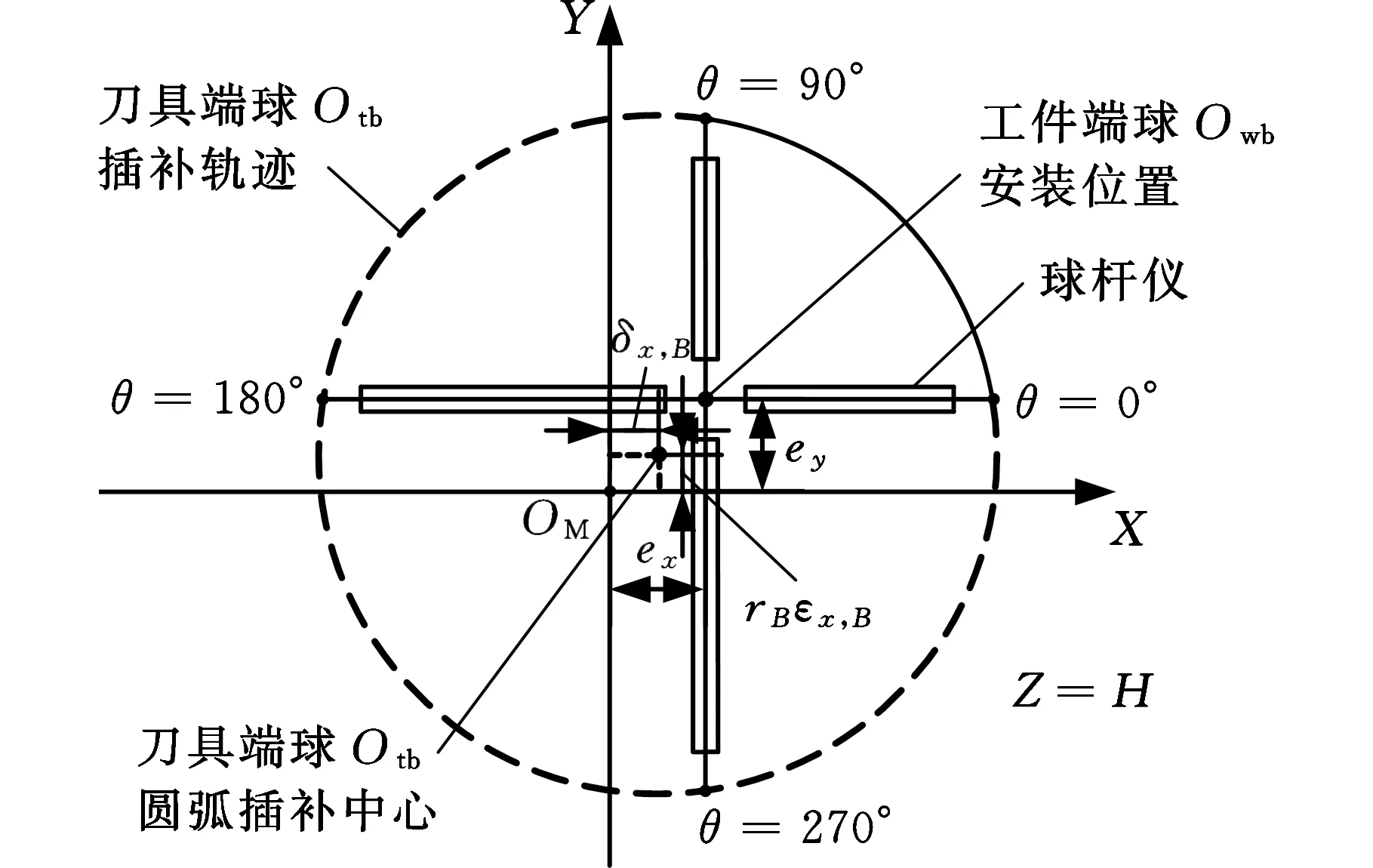
图6 C轴静止时球杆仪运动示意图
式(11)中包含2项B轴PIGE,为便于求解,需利用4个特定相位处球杆仪的Δl,取θ分别为0°、90°、180°和270°。进而,δx,B和εx,B可以借助下式进行辨识:
(12)
为辨识C轴PIGE包含的6项误差元素,还须借助图5所示切向及轴向测量策略。
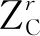
ΔlED,C≈0
(13)
故仍可基于式(8)辨识EI,C。对应各测量策略,将第1节中各PIGE定义代入式(8),整理可得
(14)
ΔlEI,B可联立式(11)、式(12)求得。同理,利用特定旋转相位,可得C轴各PIGE计算方程:
(15)
式中,安装参数rC和H的下标数字表示4个特定旋转相位;Δl下标rad、tan和axi分别对应图5中径向、切向和轴向测量策略。
2.3.2PDGE辨识方法
考虑到B轴始终保持静止,因而C轴PDGE是唯一需要辨识的位置相关几何误差元素。此时,2.3.1节中辨识所得旋转轴PIGE则被视为已知参数。根据图5中各测量策略,有
(16)
则C轴各项PDGE辨识方程为
(17)
(18)
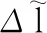
为避免由于线性相关而导致的静不定问题,安装参数rC和H需满足:
2.3.3基于迭代解耦的旋转轴PIGE与PDGE分离辨识
2.3.1节中,为辨识C轴PIGE,忽略该轴各项PDGE,当C轴转角为0时,若PDGE均为0,通过以上方法即可辨识得到旋转轴几何误差元素准确值;但是若在C轴转角为0时,PDGE不全为0,以上方法辨识的PIGE与PDGE解耦不完全,这对所提辨识方法的精准性带来一定局限性。为解决这一问题,本文提出一种迭代解耦方法来对EI,C与ED,C进行有效、精准的分离辨识。
结合式(14)可看出,EI,C对球杆瞬时长度Δl的影响随球杆旋转相位不同而不同。这表明尽管旋转轴PIGE与位置无关,但其对空间误差的影响却因位置不同而有所区分。其中,δx,C、δy,C、εx,C和εy,C对Δl的影响可视为一类随旋转角度变化的谐函数;而δz,C和εz,C对Δl的影响则可分别视为一类线性和角度的常量偏移。由此可推断,初始辨识所得ED,C中存在由EI,C所致的耦合成分,即
(19)
式中,上标c、d、r分别表示含耦合项C轴PDGE、解耦的C轴PDGE和C轴残余PIGE。
考虑到残余EI,C的谐波效应和偏移效应,通过式(17)初步辨识的ED,C可以表示为以下形式:
(20)
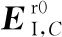
根据EI,C的残差效应,采用一阶离散Fourier拟合ED,C(0),ED,C(0)可以表示为
(21)
式中:a0(0)、a1(0)和b1(0)为常系数;$1(0)、$2(0)分别视为残差EI,C引起的偏移效应分量和谐波效应分量。
因此,由式(15)辨识所得初始EI,C可写作:
EI,C(1)=EI,C(0)+a0(0)
(22)
EI,C(1)=EI,C(0)+a1(0)cosθ+b1(0)sinθ
(23)
式(22)和式(23)分别用于分离ED,C中的偏移效应分量和谐波效应分量。将式(22)、式(23)所得C轴PIGE迭代值代入式(17),对ED,C进行解耦辨识。由于PDGE可以看成偏离几何误差均值的波动量[19],所以,假设ED,C为0附近的波动量,迭代解耦过程的收敛条件可以写成
|(ED,C(i+1))ave|≤ε
(24)
式中,下标ave表示第i+1次迭代解耦所得C轴PDGE算术平均值;ε为预设收敛阈值。
一旦满足收敛条件,EI,C和ED,C即可成功解耦,从而大大提高C轴几何误差元素的辨识精度。至此,整个迭代解耦过程可以表达为图7所示流程图。
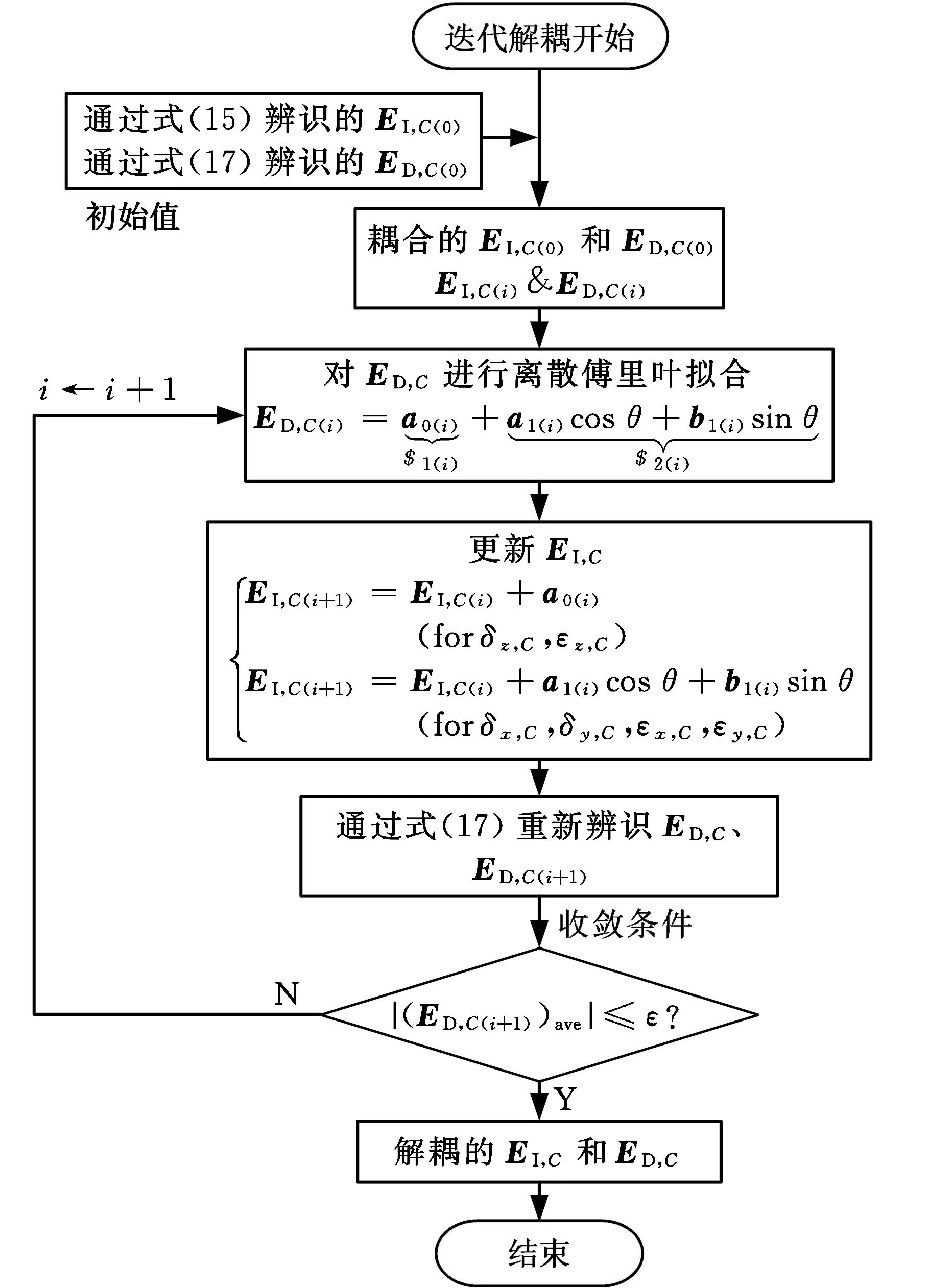
图7 C轴PIGE和PDGE迭代解耦流程图
3 区别建模辨识方法验证
3.1 仿真验证
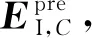
将C轴预设几何误差元素代入旋转轴运动学模型,可计算机床两运动链末端间距变化Δl;进而,利用计算所得Δl,并基于所提迭代解耦方法对C轴几何误差元素进行分离辨识。将辨识结果与预设数据分别进行对比,如表1和表2、图8和图9所示。其中,|0°表示C轴回转角度为0°时的取值;上标pre与ident_iter分别表示预设值与迭代辨识值。
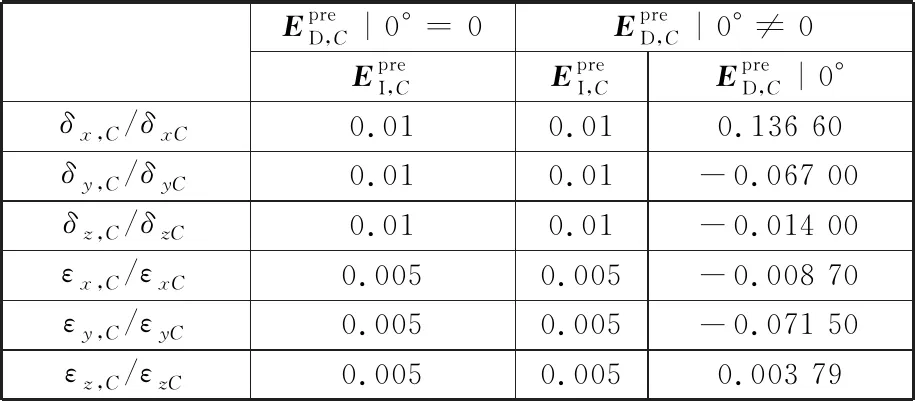
表1 预设EI,C和ED,C|0°

表2 解耦辨识所得EI,C

(a)预设
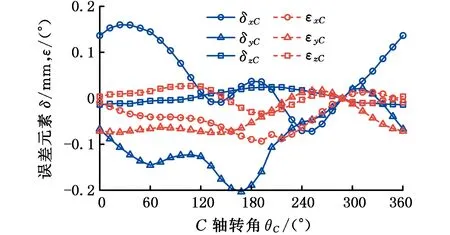
(a)预设
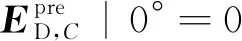
上述对比分析说明,所提迭代解耦方法能有效、精确地分离辨识机床旋转轴位置无关与位置相关几何误差元素。
3.2 实验验证
为进一步验证所提解耦辨识方法,以Renishaw QC20-W球杆仪为测量设备,在NJ-5HMC40五轴加工中心上开展几何误差测量实验,如图10所示。测量前,先通过NC代码补偿方式对直线轴几何误差元素的影响进行控制,假定直线轴没有引入误差。同时,为降低热误差对测量结果的影响,测量过程在恒温环境中进行。

(a)径向测量 (b)切向测量 (c)轴向测量
在C轴几何误差元素辨识方法中,设置了三组径向策略安装参数rC,分别为rC2、rC3、rC4,取rC2、rC4实验杆长变化测得结果进行几何误差元素辨识,取rC3实验杆长变化测量结果与预测结果进行对比。基于辨识出的PIGE和PDGE,获得杆长变化量的预估值,对比结果如图11所示。结果显示,预测结果与实测结果最大误差不超过0.005 mm,因此,所提辨识方法可以有效和准确地辨识旋转轴几何误差元素,为构建空间误差提供准确的旋转轴几何误差元素数据。
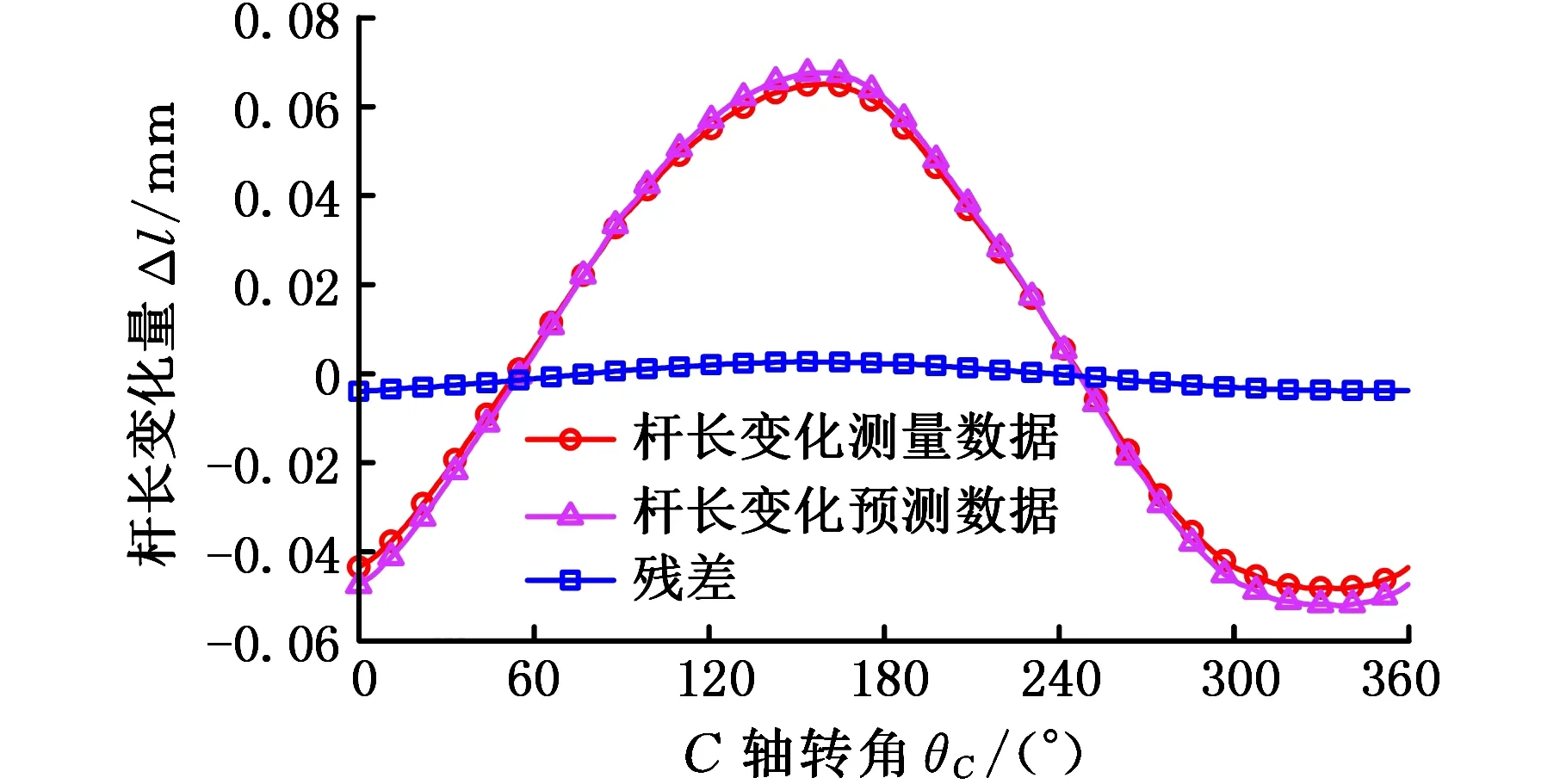
图11 测量和预测杆长变化数据对比
4 结论
精确辨识旋转轴几何误差元素是构建五轴加工中心空间误差模型的核心基础。以多体系统动力学和齐次坐标变换为理论基础,构建了BC摆头转台型五轴加工中心旋转轴运动学模型,推导了旋转轴几何误差元素辨识基本方程;借助球杆仪开展了实验研究,为求解辨识基本方程获取了必要参数,提出了一种旋转轴几何误差元素解耦辨识方法。
(1)对旋转轴PIGE和PDGE的耦合机制进行了系统分析与讨论,并在此基础上,详细阐述了基于区别建模的旋转轴位置无关与位置相关几何误差元素迭代解耦分离辨识方法体系。
(2)基于虚拟样机开展了数值仿真实验,并借此对所提解耦辨识方法进行了验证,结果对比显示,所提辨识方法能有效、精确地分离辨识旋转轴PIGE和PDGE。
(3)设置了验证实验,取一组杆长变化测量与预测结果进行对比,进一步验证了区别建模解耦辨识方法。
