大跨度斜拉桥墩塔梁固结区受力特性及结构优化

潘振宇，蔡禄荣，卢汉文

(佛山科学技术学院 交通与土木建筑学院，广东 佛山 528225)

0 概述

斜拉桥是用拉索将主梁拉到桥塔上的一种桥梁体系[1]。桥梁系统里，斜拉桥的跨越能力较强，在现有的大跨度桥型中，斜拉桥占的比率最大。斜拉桥按连接系统可以分为三大类：固结体系(墩、塔、梁固结系统)、半漂浮体系(桥墩上设支座支撑主梁系统)、漂浮体系(塔墩固结，主梁与两者无连接系统)。对于固结体系，由于桥塔、主梁、桥墩三者完全固结，因此固结部位会受到桥体传来的巨大内力。因此，对墩、塔、梁固结处的局部应力进行细致的分析研究，对同类型桥梁的结构设计与施工具有重要的意义与价值。

目前国内学者对斜拉桥墩、塔、梁固结处部位的局部应力分布进行了一些研究。夏振庭等[2]利用Midas-FEA软件对某跨径为(61m+119m+275m)的四室混合梁独塔斜拉桥墩、塔、梁固结处局部应力进行了分析；燕海蛟[3]对某跨径为(87m+160m+87m)的跨江双室双塔双索面矮塔斜拉公路桥的墩、塔、梁固结部位的施工阶段及运营阶段的局部应力进行了分析；彭定成等[4]对某跨径为(140m+2×225m+120m)的单索面三塔四跨大翼缘矮塔斜拉公路桥墩、塔、梁固结区域进行了局部应力分析；戴公连等[5]对某跨径为(32m+80m+112m)的槽型截面独塔斜拉铁路桥的墩、塔、梁固结部位进行了局部应力分析。

上述学者的研究，对同类型桥梁的设计做出了一定贡献。但美中不足的是，上述研究均采用单一尺度，得出的结果都未能很好地反映全桥对分析的固结部位的内力影响[6]。通过施加边界条件，应用大型通用有限元软件可以对结构的应力应变规律进行仿真，但是这种方法计算周期长，且对处理器的要求较高，故可以采用多尺度模型的方法来对固结部位进行分析。已有一些学者在科技期刊发表了自己的一些尝试，A.Gravouil等[7]运用局部多网格X-FEM方法进行了大型结构的三维裂纹扩展模拟；李宏男等[8]运用多尺度方法,进行了混凝土的弹塑性时程分析及局部构件损伤分析。

目前对于斜拉桥的墩、塔、梁局部应力的分析尚无涉及大跨度超宽桥面的跨铁路双塔单索面斜拉桥的分析，因此，本文通过应用新型有限元软件Midas-FEA建立实体模型，然后导入Midas-civil中的整体模型中去，基于多尺度模型分析的方法，对墩、塔、梁固结部位进行了详细的应力分析，并针对超宽桥面翼缘处应力过大且易出现应力集中的现象，给出了相应的结构优化设计方案。

1 工程概况

以某快速路上一座跨铁路，跨径布置为(99m+250m+116m)的超宽桥面双塔单索面预应力斜拉桥为工程实例。该桥设计为双向8车道，桥宽42.0m，整幅布置，中央分隔带宽4m，中心梁高3.5 m。主塔为矩形混凝土塔，左侧桥塔高60.5m，右侧桥塔高68.5m。斜拉索采用智能型平行钢绞线拉索体系(fpk=1 860MPa)，左侧桥塔每侧17对，右侧桥塔每侧20对，全桥共148根拉索。主梁采用混凝土单箱三室箱梁，主梁顶板宽度为42.0 m，底板宽度为16.0m，翼板悬臂长度为4.5 m。该桥桥型布置如图1所示。

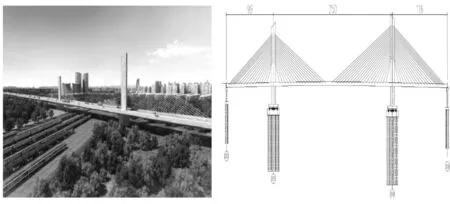
图1 桥型布置

2 有限元模型的建立

2.1 模型选取范围

根据圣维南原理[9],本文分析模型的选取除墩、塔、梁固结部位以外，主梁亦往两侧延升至距离索塔13.4 m的范围，索塔取至桥面以上15 m，下部结构取至承台底部,如图2所示。本文分析研究主要关注的内容为墩、塔、梁固结处主梁、索塔、桥墩以及墩底的应力分布情况。

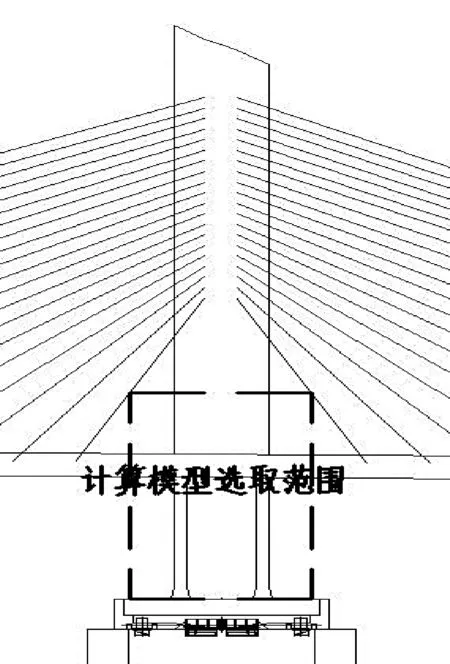
图2 有限元实体模型选取范围

2.2 局部模型

利用多尺度建模的方法，将墩、塔、梁固结部位的梁单元模型导入Midas-FEA中，可快速得到局部部位的实体模型。此次分析对索塔进行了简化处理，未考虑桥塔的过人洞，避免了软件在网格划分时因距离间隔太小而出现错误。纵横向预应力筋则通过AutoCAD导入3D线条，然后在划分网格时选择实体单元的内部线的方法进行模拟。整体有限元模型如图3所示。

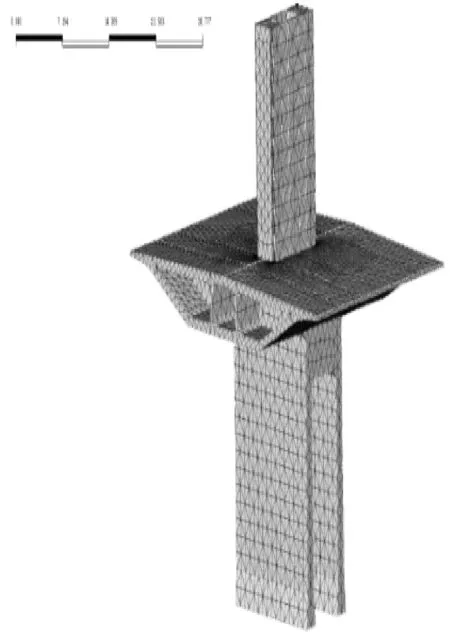
图3 塔墩梁固结部位实体有限元模型

2.3 边界条件及荷载

根据多尺度建模的基本理论，将划分网格后的实体模型导入Midas-civil中的全桥模型中，整体模型与实体模型连接处的节点作为主节点，与同一截面的实体单元节点之间添加刚性连接，可以较好地模拟全桥对局部模型的实际内力传递。截面内力见表1。

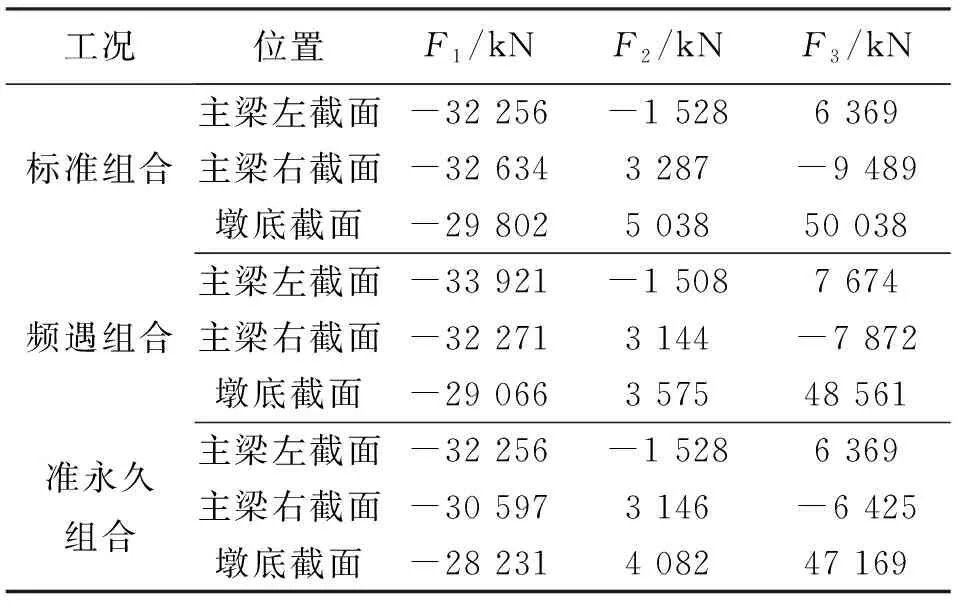
表1 截面内力

本文考虑了成桥阶段的荷载工况。施加到整体模型上的静力荷载包括：自重、拉索索力、纵横向钢束预应力、二期恒载、成桥压重、墩、塔、梁固结处的横向预应力、桥塔的环向预应力。移动荷载根据城-A标准，横桥向取8车道布载，包括施加到主梁中心线的中载以及施加到8车道的偏载两种工况。

3 应用分析

由于篇幅限制，选取较为不利的组合进行介绍。对于标准组合、频遇组合、准永久组合三种荷载工况的应力分析结果见表2。

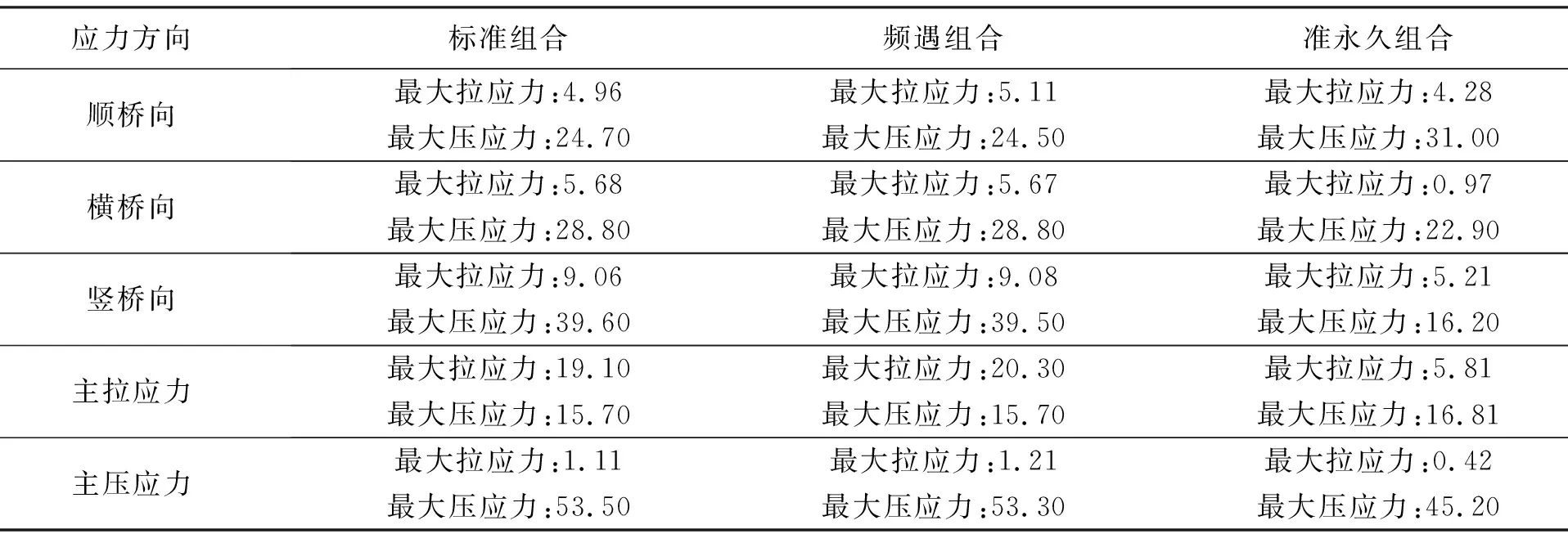
表2 两种工况下的应力值 (单位：MPa)

实体有限元模型分析结果如图4～图8所示。由于篇幅限制，本处仅给出最不利荷载工况作用下顺桥向应力、主拉应力、主压应力云图以及主拉与主压应力中超出规范限制数值的应力分布图。由图4可见，实体有限元模型在荷载作用下，顺桥向固结部位整体受压，应力大小分布均匀，出现的超出限值的部位，只有梁墩固结交线处极少个单元，对结构整体影响较小，可忽略不计。最大拉应力为4.96MPa，最大压应力为24.67MPa，超出规范对拉应力的限值2.446MPa的部位仅出现在墩底混凝土表面。

图4 顺桥向应力云图

由图5和图6可知，实体有限元模型最大的主拉应力为19.6MPa，位于墩梁固结连接的外转角处。在固结部位的各个交界处均出现了不同程度的拉应力集中现象，大小在2. 47～5.39MPa之间。由于翼缘顶板厚度仅为20cm，使得此处出现了应力集中现象，部分单元的拉应力超过了规范限值。

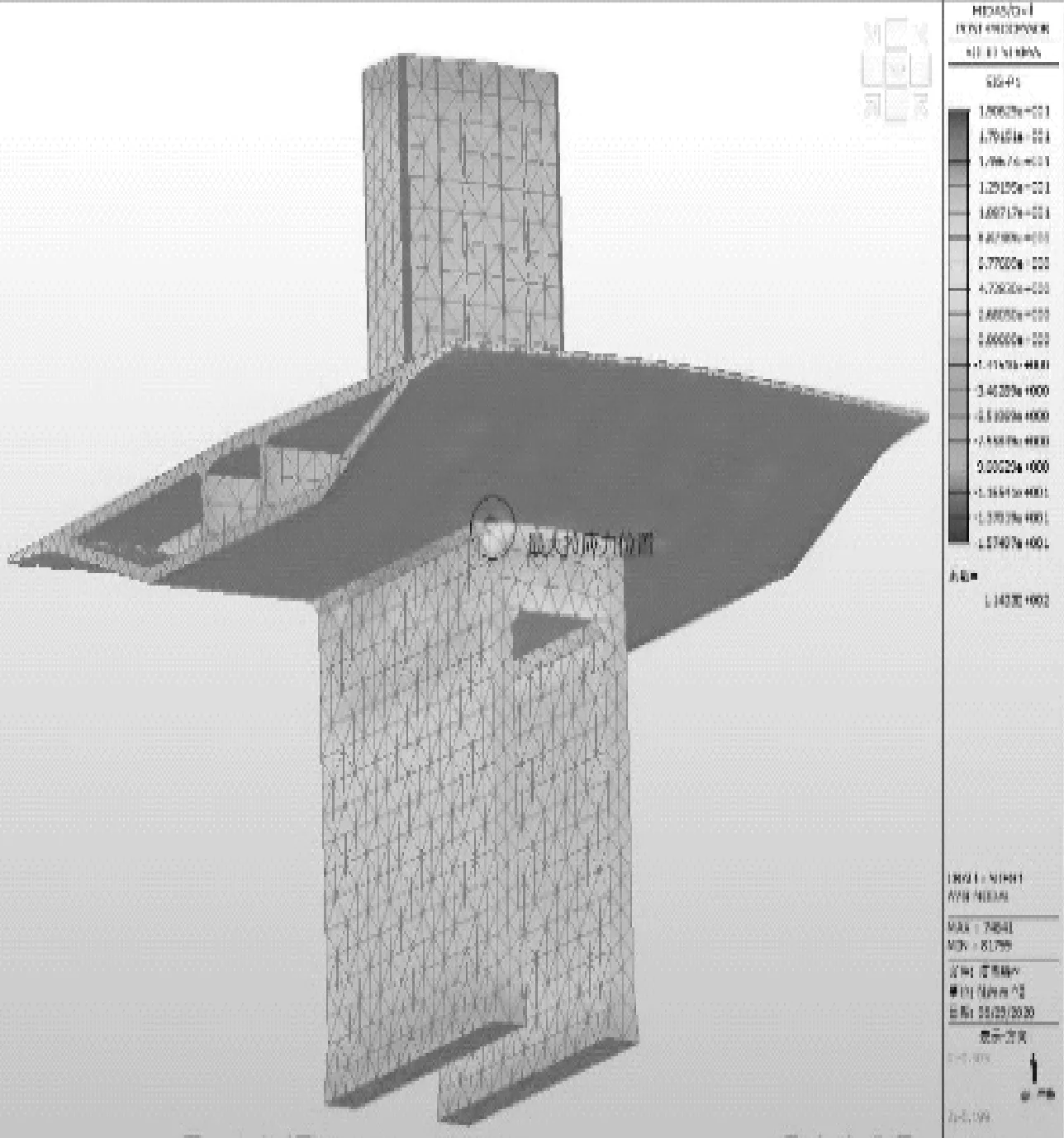
图5 主拉应力云图

图6 主拉应力超限分布云图

由图7和图8可知，实体有限元模型最大主压应力为53.539MPa，位于塔梁固结交界转角处。这是由于该处转角倒角设置偏小，导致了应力的过于集中，在实际施工中应予以修正，避免出现这种情况。压应力主要分布在8.53～18.2MPa。在塔顶、墩底转角处出现了应力集中现象，压应力大小超过了规范限制，大小在21.3～26.9MPa，对整体影响较小。

图7 主压应力云图

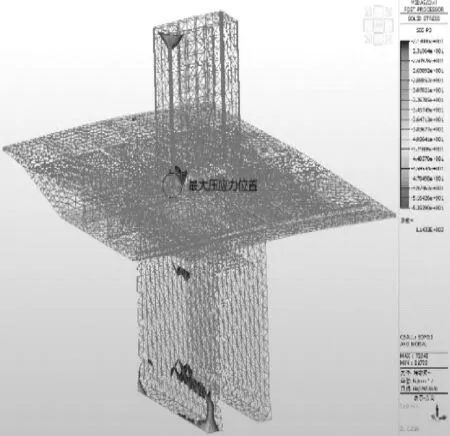
图8 主压应力超限分布云图

4 设计优化

由图9可以看出，原结构箱梁翼板厚度只有20cm，在此处出现了应力集中现象，导致该部位混凝土主拉应力超过规范限值，且该部位横隔梁宽度为0.6m，设置了5个横隔板，刚度较小。由于墩、塔、梁固结部位受到的全桥带来的内力很大，导致翼缘板边缘易产生较大的拉应力并伴随着应力集中现象的出现。

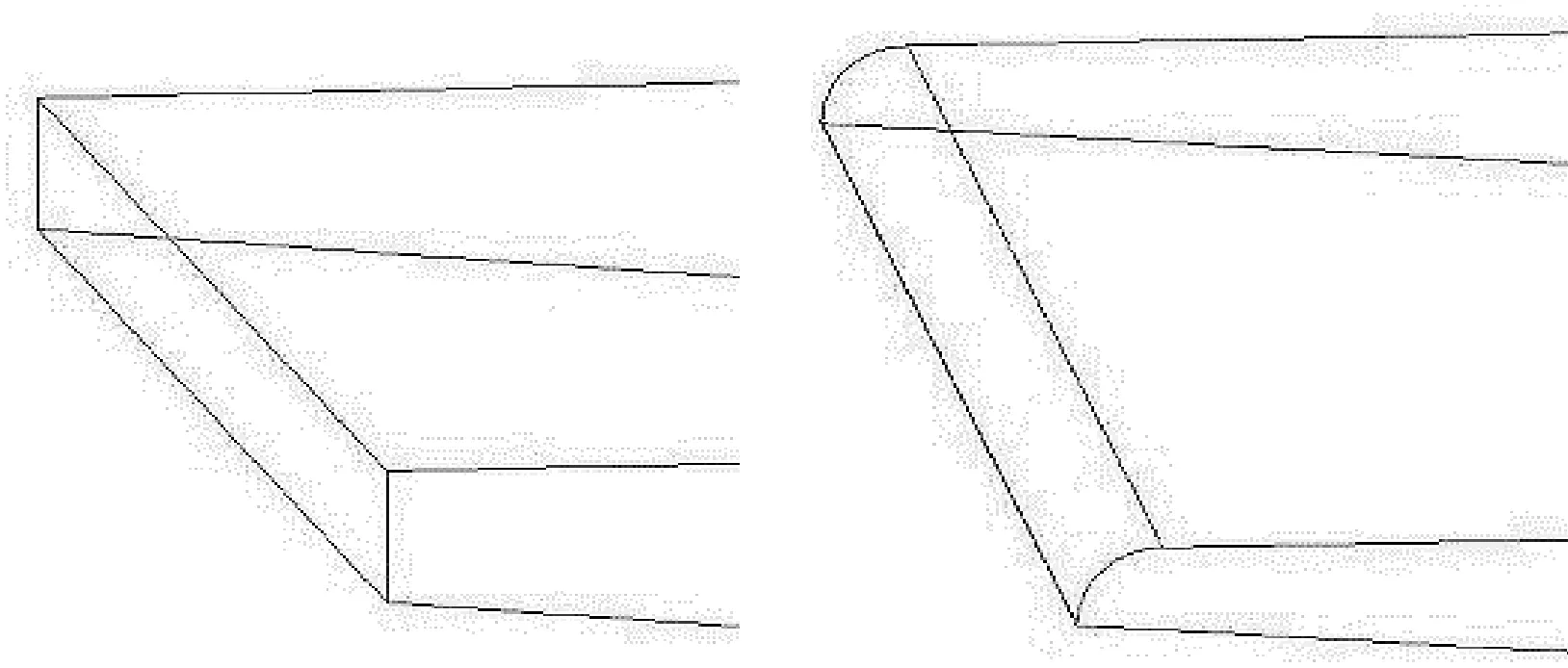
图9 设计优化

对于箱梁结构优化设计的方案有很多，彭定成等[4]通过增加横梁加劲肋数量的方法使得翼缘处的拉应力大大降低；董建松[10]通过适当减小横隔板的间距，使得应力分散，缓解了桥面板与横隔板接触处的应力集中现象。而本文选用的是单箱三室箱形截面主梁，由于设计的原因，不易在结构上增加加劲肋，因此采取在翼板边缘增加半径为20cm的圆弧倒角，并将横隔板宽度增加至0.8m、数量增加到8个的方法，对结构进行优化。

改进前后应力分布情况如图10所示。构造改进后翼缘板边缘最大主拉应力由19.06MPa下降至9.81MPa，相比原设计方案降幅49%左右，优化效果非常明显。并且翼缘的应力集中现象也得到了改善，降低了混凝土开裂的几率。

图10 改进前后主拉应力比较

5 结论

基于Midas-FEA软件，运用多尺度分析方法，对某大跨度斜拉桥的墩塔梁固结部位进行了详细的局部应力分析，得到以下结论：

(1)多尺度法能较好地解决边界条件如何选取的问题，通过对计算结果的分析，可以发现墩塔梁固结部位与整体模型连接部位能很好地进行应力传递。

(2)固结部位平均应力分布较均匀，整体应力水平在规范限值以下。

(3)结构在翼缘位置、塔梁交界转角处以及梁墩交界处出现了应力集中和拉压应力超限现象。

(4)针对翼缘部位应力集中和拉应力超限现象给出了优化设计。优化后的结构分析结果显示，在翼缘处设置圆弧倒角能有效地避免应力集中现象出现。对于塔墩梁固结部位受到很大内力作用，需在该处增加横隔板的密度与宽度，并考虑增加布设钢筋的数量。