曲线寒区隧道保温层铺设长度计算方法研究

王志杰，姜逸帆，李金宜，蒋新政，周 平, *，雷飞亚

(1. 西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031；2. 西南交通大学土木工程学院，四川 成都 610031)

0 引言

随着我国基础设施建设的不断发展，大量公路隧道在高海拔、高寒等恶劣条件下进行修建。寒区隧道通常受到季节性冻融、冻胀作用的影响，给隧道的安全运营带来了极大的风险。目前，为了解决隧道冻害问题，国内较为常用的抗防冻措施为铺设保温层。相关研究也证实了保温层的有效性[1]。

受空气流动影响，寒冷空气对隧道的影响会延伸至洞内一定深度。为保证隧道在运营期间不出现冻害，需要对寒区隧道的纵向温度场分布和保温层的铺设长度展开研究。

现场实测作为最直接的研究方法，被广泛应用于温度场研究。Wheeler等[2]通过现场测试研究了隧道风速与温度场的均匀性，并得出了空气速度对隧道温度场的影响规律。Yan等[3]通过对德格隧道进行监测，结合数值模拟等研究方法，得出隧道内温度场的时空演化规律。高焱等[4]通过现场实测，明确了绥阳隧道的纵向温度场及风速分布状况。

为了更深入地研究温度场分布规律，国内外学者展开了大量的理论研究。Kawamura等[5]根据叠加原理和能量守恒定律，建立了寒区隧道洞内空气流体和围岩固体对流换热的计算模型，并给出该计算模型的解析解。Krarti等[6]通过对某地下风洞进行研究，得到了地下洞室的温度场解析解，并用温度的年振幅和年平均气温2个参数对温度场特性进行了表征。何春雄等[7]建立了隧道内空气与围岩对流换热及固体导热的综合模型，分析预报了祁连山区大坂山隧道开通运营后的围岩温度分布情况。韩跃杰等[8]通过建立隧道纵向洞内空气与洞壁的气固耦合传热模型，计算得到了隧道的纵向温度场分布情况。

随着计算机软件的普及，通过软件模拟隧道的温度场也成为了更多学者的选择。郑阳等[9]通过Fluent与Ansys的假耦合计算，建立隧道围岩、衬砌及洞内气体的流固对流换热模型，得出了隧道围岩的温度场分布情况，并验证了高寒隧道保温层的必要性。贾辉[10]通过CFD数值模拟计算，分析了气象因素对寒区隧道温度场的影响规律及相关性。

对于如何合适地选取保温层的铺设长度，部分学者展开了相应研究。孙文昊[11]根据现场测温结果，得到洞内空气温度的分布特征，综合考虑保温层的隔热效应修正和边界效应修正，得到隧道保温层铺设长度的计算公式。夏才初等[12]基于由隧道进、出口气象条件及隧道地形条件求解的温度场解析解，提出了一种保温层铺设长度计算方法。高焱[13]统计分析了大量寒区隧道的冻害情况，对设防长度与洞口气温关系进行拟合分析，得到了设防长度的统计规律。

目前已经有不少学者展开了寒区隧道纵向温度场的研究，且结果较为成熟，但是如何计算保温层设防长度，还处于一个不断探索的阶段。随着国家公路建设的发展，由于地形和选线的原因，不可避免地出现大曲率曲线隧道，甚至螺旋隧道，现有的研究没有涉及曲线隧道的温度场计算及对应的保温设计需求。为了探究曲线隧道的保温层铺设长度计算方法，本文采用文献调研、理论推导、数值模拟的方法，对曲线螺旋隧道的温度场展开研究，结合理论推导提出一种较为可靠的曲线寒区隧道保温层铺设长度计算方法。

1 工程概况

金家庄特长螺旋隧道为河北省政府和交通运输部“一号工程”——延崇高速公路的重点控制性工程，其入口位于赤城县炮梁乡金家庄村西北方向，出口位于崇礼区棋盘梁村，左幅长4 228 m，右幅长4 104 m。隧道设斜井1处，长750.95 m，按双向4车道高速公路标准建设，最大行车速度为100 km/h。建设螺旋隧道，能解决隧道进出口的大高差和路线纵坡太大的问题，保证车辆安全行驶。隧道设计曲率半径达到890 m，隧道平面示意图见图1。

图1 金家庄特长公路隧道平面示意图

隧址区位于大陆性季风气候中温带亚干旱区，四季分明，冬季寒冷漫长，降雪量较少。全年日照时间长、温差大，风向以西北风和静风为主。年均降水量在424 mm 左右，且分布不均，全年无霜期平均为115.9 d。年平均气温为5.5 ℃，年最髙气温为39.4 ℃，最低气温为-28.2 ℃，最大积雪深度为9 cm，最大冻土深度为162 cm，无霜期为145 d。

2 直线隧道保温层铺设长度计算公式

2.1 计算假设

隧道是一个复杂的结构体，隧道内的空气流动形式也同样复杂。为了得到隧道保温层铺设长度的计算公式，进行如下假设：

1)研究对象达到平衡状态，即为稳态问题；

2)只考虑径向传热，忽略隧道空气纵向对流换热；

3)所有材料均为各向同性，且导热系数、比热容、密度不随温度变化；

4)不考虑二次衬砌与初衬、衬砌与围岩之间的接触热阻，接触边界处满足温度和热流量相等的连续条件；

5)将复杂的传热问题简化为带有对流换热边界的三维多层圆筒壁的热传导问题，将隧道、衬砌及围岩断面简化为圆形或圆环。

2.2 传热模型

多层圆筒传热模型作为求解传热模型的经典模型，已经被引入隔热层厚度计算[14]。对于厚度计算求解，使用一维传热模型即可； 而对于铺设长度的计算，需要引入三维模型，考虑纵向方向的温度传递。因此，本文采用三维的多层圆筒传热模型。

简化后的传热模型如图2所示。

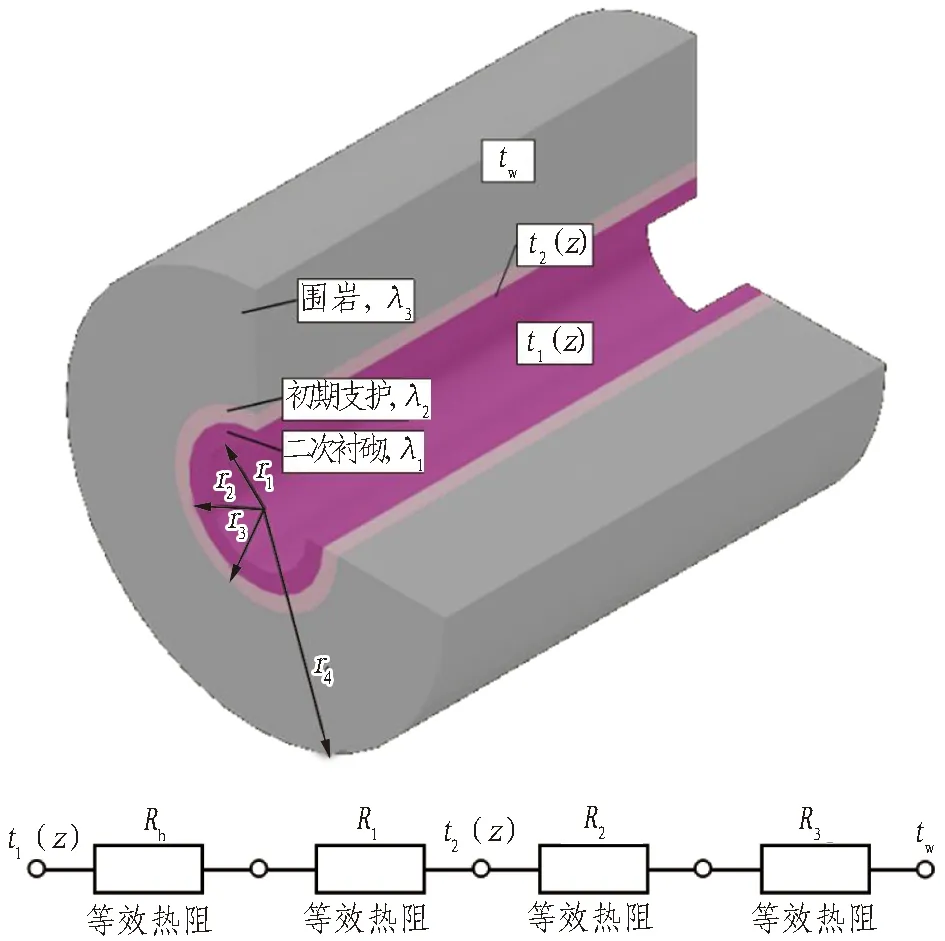
r1、r2、r3、r4分别为二次衬砌与空气交界面、初期支护与二次衬砌交界面、初期支护与围岩交界面、围岩恒温边界距圆筒中心的距离； λ1为二次衬砌的导热系数； λ2为初期支护的导热系数； λ3为围岩的导热系数； t1(z)为进洞深度z(m)的空气温度； t2(z)为进洞深度z(m)的衬砌背后围岩温度； tw为进洞深度z(m)的深处围岩恒温温度。

2.3 直线隧道保温层铺设长度计算公式推导

1)根据已有的研究，多层圆筒传热模型径向的传热基本方程为：

(1)

式中：Q为热通量；R为圆筒内外两侧的热阻； Δt为圆筒内外两侧的温差。

(2)

式中：Rh为单位长度空气围岩换热等效热阻；R1为单位长度二次衬砌支护等效热阻；R2为单位长度初期支护等效热阻；R3为单位长度围岩等效热阻。

(3)

式中hc为对流换热系数。

(4)

(5)

(6)

2)为了计算纵向的温度传递，本文做如下处理。如图3所示，取空气微元dz，空气吸收围岩带来的能量为Φ，空气温度由t1(z)变为t1(z+Δz)，空气微元dz温度变化的控制方程为：

(7)

式中：ρ为空气密度；c为空气比热容；A为隧道断面面积。

图3 空气微元吸热示意图

根据圆筒传热方程，围岩传向空气的热量即为空气吸收的热量，所以微元dz吸收的热量

(8)

式中v为空气速度。

3)边界条件为：

(9)

式中t0为洞口空气温度。

4)保温层铺设长度计算：

联立式(7)—(9)可得

(10)

求解微分方程得

(11)

则二次衬砌背后温度

(12)

由式(12)可以得到保温层铺设长度

(13)

3 曲线隧道保温层铺设长度计算公式修正

3.1 对流换热系数的影响

表面对流换热系数的数值与换热过程中流体的物理性质、换热表面的形状、部位以及流体的流速等都有密切关系。物体表面附近的流体的流速越大，其表面对流换热系数也越大。计算传热系数的方法主要有试验求解法、数学分析解法和数值分析解法。

国内已有学者对混凝土的对流换热系数进行了试验求解。张建荣等[15]利用风洞探究了不同风速下的对流换热系数hc，总结出如下关系式：

hc=3.06v+4.11 。

(14)

不同曲率的隧道在环境温度以及初始地温、断面大小等相同的情况下，其对流换热的差异可以简化认为是由空气速度的差异造成。

3.2 空气速度的影响

利用CFD软件Fluent探究不同曲率隧道的空气速度影响。

3.2.1 模型的建立

采用控制变量法，保持隧道总长度(4 220 m)不变，为了使隧道围岩外边界温度保持为原始岩温，所建模型的横断面尺寸应超出调热圈范围[16]，计算模型横断面采用边长40 m的正方形区域，隧道净空面积为85.42 m2。本文模型的初始温度场通过UDF赋予初始地温实现，所赋予的初始地温考虑了洞外空气温度以及地热的影响，因此，赋予初始地温后的模型不再考虑边界温度的影响，采用绝热边界。通过改变隧道曲率半径，设置曲率半径r为900、1 800、2 700、3 600、4 500、5 400、6 300 m的螺旋隧道及同长度直线隧道共8个工况。隧道模型如图4所示。

(a) 工况1： r=900 m螺旋隧道(b) 工况2： r=1 800 m螺旋隧道

(c) 工况3： r=2 700 m螺旋隧道(d) 工况4： r=3 600 m螺旋隧道

(e) 工况5： r=4 500 m螺旋隧道(f) 工况6： r=5 400 m螺旋隧道

(g) 工况7： r=6 300 m螺旋隧道(h) 工况8： 直线隧道

(i) Fluent计算模型 (单位： m)

3.2.2 初始地温的计算

由于隧道从进口到出口各处的埋深不同，造成了隧道全线不同位置的初始地温存在差异，因此，准确地模拟出初始地温可以提高计算的准确性。本文采用的初始地温处理流程如图5所示。

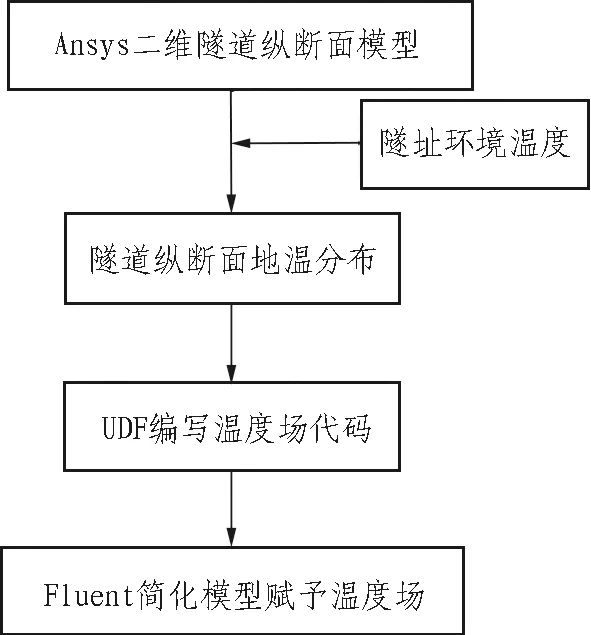
图5 初始地温处理流程

根据气象部门提供的隧址区大气温度数据及现场气象站监测数据，绘制日平均温度变化时程曲线。通过三角函数对隧址区日平均温度时程变化曲线进行拟合，拟合函数如下：

Temp(t′)=5.5-20.5sin(2πt′/365) 。

(15)

式中： Temp(t′)为隧址区洞口处大气温度拟合函数，℃；t′为时间，d。

确定初始温度场时，模型的初始温度考虑地热，将模型在年温度周期循环200年后的温度场作为金家庄特长公路隧道初始地温场，根据地质调查图纸，利用Ansys建立平面二维模型。模型的边界条件加载如下： 模型上边界与大气接触，边界条件设定为随时间动态变化的温度变化荷载Temp(t′)； 下边界与深处的地层存在换热，设为热流密度边界，根据相关文献热流密度取q=0.06 W/m2； 模型左、右边界由于与接触的围岩处于同一埋深，受外界环境的影响相同，因此，假设没有热量的传递，设为绝热边界。金家庄特长公路隧道初始地温场计算模型及边界条件如图6所示。

(a) 数值计算模型

(b) 数值计算边界

图7为计算得到的200年后金家庄特长公路隧道冬季(1月1日)温度场分布云图。

图7 金家庄特长公路隧道冬季温度场分布云图(单位： ℃)

图8示出金家庄特长公路隧道中间深埋段冬季(1月1日)围岩温度场分布曲线。由图可以看出，在隧道的中间深埋段，围岩温度随里程变化较小(12.5～13.5 ℃)，围岩温度分布曲线表现出与地形相似的几何特征，即中间高、两端低的分布趋势。

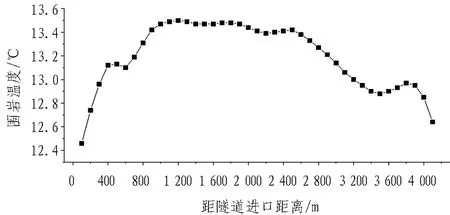
图8 金家庄特长公路隧道中间深埋段冬季围岩温度场分布曲线

图9示出金家庄特长公路隧道进出口浅埋段冬季(1月1日)围岩温度场分布曲线。由图可以看出： 隧道洞口段(100 m范围)温度分布受外界气象温度影响明显，随着进洞深度的增加，隧道衬砌位置的围岩温度出现迅速增大的趋势，变化幅度接近6 ℃，在建模计算过程中不可忽略。为了得到更加符合实际的围岩温度初始条件，通过函数拟合的方式得到隧道进出口段的围岩温度随进洞深度x变化函数，拟合公式为：

(16)

将拟合的温度场采用UDF编程，赋予Fluent简化模型。隧道入口和出口段的初始温度场如图10所示，基本符合实际初始地温。

(a) 隧道进口围岩初始温度

(b) 隧道出口围岩初始温度

(a) 隧道入口 (b) 隧道出口

3.2.3 计算参数

根据隧址区日平均温度时程变化曲线的拟合函数，设置洞口气温为隧址区最冷月平均气温-15 ℃； 根据隧道自然风要求，进口风压设为28.49 Pa(对应风速2 m/s)，进口风速取单向持续通风60 d计算。热力学计算参数如表1所示。

表1 热力学计算参数

3.2.4 计算结果分析

不同工况(隧道曲率半径不同)的空气速度断面图见图11。

通过对比不同曲率半径的空气流速特点，可以得出以下结论：

1)由于曲率的影响，空气在隧道内流动中会受到离心力的作用，向曲率隧道的外侧偏移，挤压气体，使外侧的气体拥有更高的流动速度，而内侧的气体流速相对减小。

2)曲率与速度的偏移程度正相关，曲率越大速度的偏移现象越明显。

根据不同曲率半径螺旋隧道及直线隧道的计算结果，在进洞50、150、300、500、800、1 100、1 500、2 000 m深度位置共设置8个监测断面(编号1—8)，布置从隧道左侧到右侧的测线，可以得到不同曲率半径隧道在不同进洞深度的断面空气速度分布曲线，如图12所示。

根据图12可以得到以下结论：

1)速度的偏移现象需要在空气流进入隧道一定深度后才会出现。一般是在第2个断面即洞深150 m后才出现偏移，且偏移发生后会迅速达到稳定状态，即隧道中的空气流动将保持持续的偏移状态。

2)由于混凝土壁面的摩擦影响，空气在边界层位置的速度明显小于非边界位置的速度。偏移作用的挤压加速效应在边界层上依然适用，依然呈现曲率越大、速度偏移越大的规律。

由于与混凝土发生对流换热的空气处于边界层，因此，研究边界层的空气速度更有意义。其空气速度越大，设防长度越长。图13示出不同曲率半径隧道的边界层空气速度曲线。

(a) 工况1： r=900 m螺旋隧道 (b) 工况2： r=1 800 m螺旋隧道

(c) 工况3： r=2 700 m螺旋隧道 (d) 工况4： r=3 600 m螺旋隧道

(e) 工况5： r=4 500 m螺旋隧道 (f) 工况6： r=5 400 m螺旋隧道

(g) 工况7： r=6 300 m螺旋隧道 (h) 工况8： 直线隧道

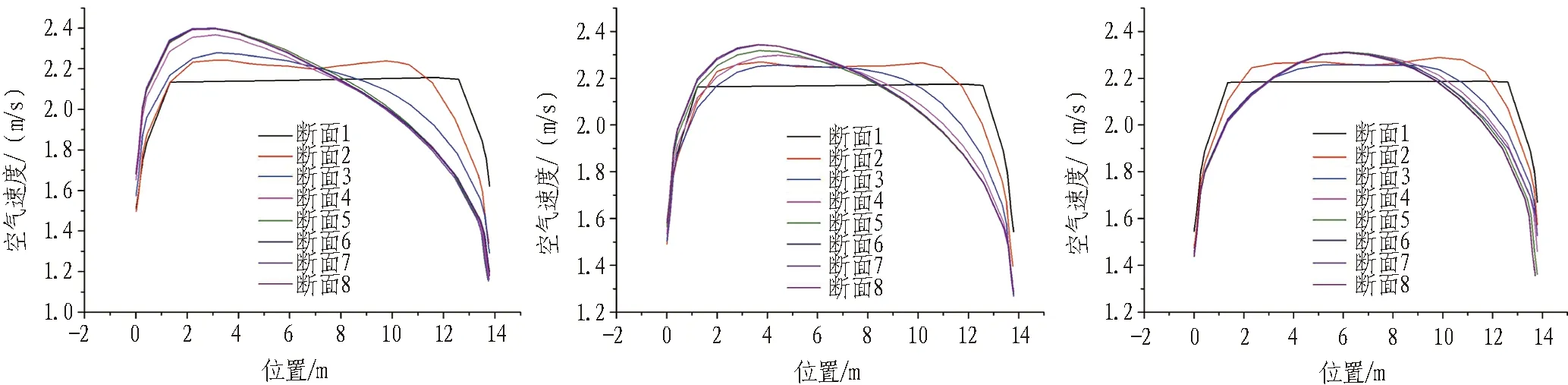
(a) r=900 m螺旋隧道 (b) r=1 800 m螺旋隧道 (c) r=2 700 m螺旋隧道

(d) r=3 600 m螺旋隧道 (e) r=4 500 m螺旋隧道 (f) r=5 400 m螺旋隧道

(g) r=6 300 m螺旋隧道 (h) 直线隧道

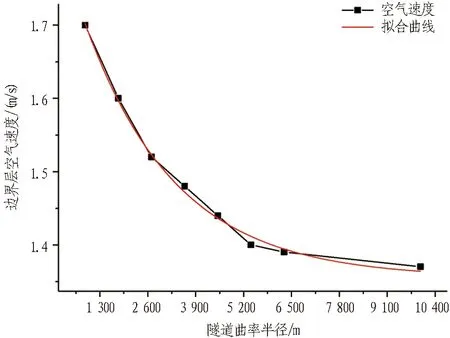
图13 不同曲率半径隧道的边界层空气速度曲线

对图13曲线进行拟合，拟合度为0.996，拟合效果良好，拟合公式为：

(17)

式中r为隧道曲率半径。

3.3 曲线隧道的保温层铺设长度计算公式

将得到的隧道曲率半径与边界层空气速度的拟合公式(17)以及混凝土对流换热系数公式(14)代入保温层铺设长度计算公式(13)中，得到：

(18)

4 曲线隧道保温层铺设长度计算结果

根据曲线隧道保温层铺设长度计算公式(18)可以得到不同曲率半径隧道的保温层铺设长度，如表2所示。

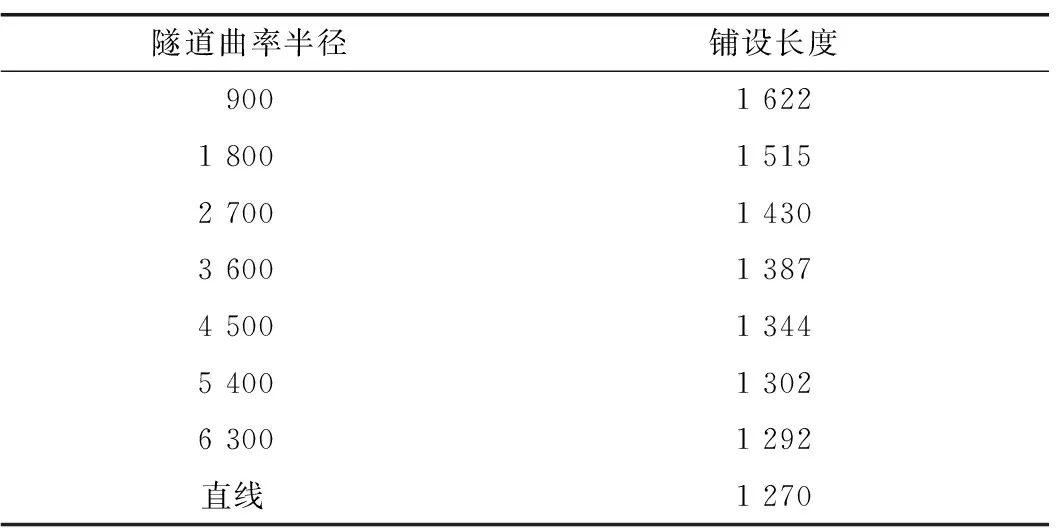
表2 不同曲率半径隧道的保温层铺设长度

不同曲率半径的隧道二次衬砌背后温度数值模拟结果如图14所示，二次衬砌背后冻深长度模拟计算结果如表3所示。

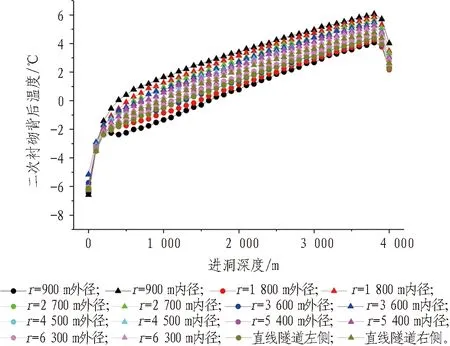
图14 不同曲率半径的隧道二次衬砌背后温度曲线数值模拟结果

表3 二次衬砌背后冻深长度模拟计算结果

将数值模拟计算结果与公式计算结果进行对比，如图15所示。

图15 保温层铺设长度数值模拟计算与公式计算结果对比

可以看出，曲线隧道的保温层铺设长度公式计算结果与数值模拟计算结果对比，呈现相同的变化规律，且铺设长度随曲率半径的变化规律大致相同，证明了计算公式的可靠性。

5 结论与讨论

本文依托金家庄隧道，通过圆筒传热模型推导保温层铺设的理论计算公式，并利用CFD软件探讨了不同曲率半径隧道温度场分布规律以及保温层长度铺设规律，得出了曲率影响隧道温度场的关键因素，结合理论推导得出了曲线隧道保温层铺设长度计算公式。

1)根据圆筒传热模型推导出的保温层铺设长度计算公式可以发现，不同的隧道曲率对铺设长度的影响主要反映在对边界层空气速度的影响。不同的空气速度影响了空气与混凝土衬砌的对流换热系数以及空气受热加热时间，进而影响了温度的传递。

2)通过数值模拟，发现曲线寒区隧道受曲率的影响，隧道内断面空气峰值速度在离心力的作用下向隧道外侧偏移，偏移程度与曲率半径正相关。空气的偏移对外侧的边界层产生挤压效应，加速了外侧边界层的空气流动速度。偏移效应一般在隧道进洞深度150 m出现并迅速达到稳定。

3)通过温度场分析，曲线隧道的温度场分布沿隧道轴线呈非对称分布，外侧边界层空气在离心力作用下加快了对流换热，因此，外侧的冻深长度大于内侧，在实际设防时应重点关注外侧的衬砌背后温度变化情况，且隧道曲率越大该现象越明显。

4)根据圆筒传热模型推导出的保温层铺设长度计算公式，是一种简化计算公式。该计算公式可用于计算不同曲率半径隧道的保温层铺设长度，与数值模拟结果对比，呈现相同的变化规律，但计算结果较为保守，能够满足对抗防冻的铺设长度要求，在实际应用时可考虑20%的折减。后续建议耦合多种影响因素对保温层的铺设长度进行研究。